基于贝叶斯网络的基因变异间的因果关系发现与验证
蔡瑞初 甄启祺 陈 薇 郝志峰,2
1(广东工业大学计算机学院 广东 广州 510006)2(佛山科学技术学院数学与大数据学院 广东 佛山 528000)
0 引 言
全基因组关联研究(Genome-Wide Association Study,GWAS)当前主要侧重于单核苷酸多态性(Single Nucleotide Polymorphisms,SNPs)与人类疾病的关联研究[1]。研究表明,人类常见疾病的复杂性状涉及多个基因变异之间的相互影响,而基因变异间存在连锁不平衡(Linkage Disequilibrium,LD)现象[2]。由于基因按一定次序在染色体上呈线性排列,关于基因变异间的相互作用大多是从基因的相对物理位置来探讨,然而在基因测序数据中,一些位于不同染色体上的基因,其测序数据都反映出了非偶然性的连锁不平衡现象[3],单纯研究相邻基因之间变异的相互作用会很受局限,故多基因变异相互影响是GWAS中不可回避的关键问题。
在多基因变异间的相互作用研究中,Yang等[4]提出了多变量全基因组关联测试的方法,对多变量定量表现型数据进行分析。这是一种线性混合模型,实验表明,该方法较好地把第一类错误控制在合理范围内,并且比不同族群结构和相关性的边缘检验更有效。然而该方法的适用条件为变量之间满足线性关系,该假设较为苛刻。
事实上,由于多个基因变异之间的相互作用效果并不是简单地线性加权,传统的线性模型远不能满足这种多基因模型[5]。Monneret等[6]着重于边缘因果估计方法,提出了基于高斯结构方程的高斯因果模型,然而该模型是一种线性模型,与真实情况中基因相互影响的非线性并不符合。
立足于非线性角度,Botta等[7]对随机森林进行扩展,得到T树模型。通过实验与线性模型相比,T树的预测能力表现出明显优势,并表明了多个SNPs之间的非线性效应。在进一步的基因座识别研究中,T树模型不仅复现了已发现的多数基因座,并且发现了与克罗恩病相关的两个新的符合生物学的易感位点。而在更复杂的非线性关系如网络关系的研究中,T树的效果有待验证。Lim等[8]提出了BTR(BoolTraineR)算法,对布尔模型进行了优化,使用单细胞数据重构了基因调控网络,然而没有进一步考虑基因调控和基因变异之间的关系。
在基因变异和基因调控方面,现有的研究主要关注具体基因与疾病之间的关系。在基因变异上,Pan等[9]阐明了基因TNNT2其新变体R205Q的因果作用,Elsaadany等[10]通过全外显子组测序研究了WWOX基因中的新纯合突变,并提出了WWOX基因变异与人类癫痫性脑疾病之间的关系。基因调控方面,Wang等[11]研究了N6-甲基腺苷对脂肪的生成代谢起到了关键的调控作用,Jin等[12]研究了microRNA-192对膀胱癌细胞的调控,表明microRNA-192可能可以通过调控细胞周期,从而抑制膀胱癌细胞。Liu等[13]在Sia等[14]的基础上构建了CNV-ICC-TRN,结合KEGG信号通路进行分析,发现基因变异的影响会发生在通路组件上。Liu等认为,整合基因变异和调控网络二者的信息可更深层次地研究肝癌致病机理,然而目前基因变异和基因调控这两者关系的相关成果相对较少,是当前亟需进行的研究。
鉴于上述研究状况,针对部分不足,本文对基因变异间的因果关系进行研究,发现在同一信号通路中相互调控的基因,其变异间具有较强的因果性。本文通过改进的Parents-Children(Improved Parent-Children,IPC)算法,检测出具有直接相互作用的基因对,并通过结构识别的方法判断出因果方向。实验结果表明,相互调控的基因变异之间具有较强因果性。本文还发现了一批具有较强因果性的基因变异可供相关研究参考。
1 相关知识
1.1 SNP与基因
单核苷酸多态性(Single-Nucleotide Polymorphism,SNP)指在基因组中某特定位点上的单核苷酸所发生的变异,该变异在人类群体中占有一定的规模比例[15]。在多代遗传中,SNPs一般都会稳定地遗传下去,故在GWAS中,一些跟人类疾病相关联基因的变异,可以用SNPs作为稳定标记。
基因是一段DNA序列,由多个脱氧核糖核苷酸组成,是生物体的遗传分子。人体的性状由基因和生活环境控制调节,其中基因起着决定性作用。不同基因的DNA序列长度并不相同,而SNP是对单核苷酸状态的描述,由此容易得知,基因与SNP之间是属于一对多的关系。
1.2 信号通路
在多细胞生物体内,细胞外的细胞因子、激素等分子信号特异性地与细胞膜结合或直接穿过细胞膜,经过级联转导后多种信号在细胞内相互识别作用,共同调控内部的生化反应。细胞内多种信号的作用途径交织成各种错综复杂的调控网络,进行生化功能的调控,这样的网络称为信号通路(Signal Pathway)[16]。京都基因与基因组百科全书通路(Kyoto Encyclopedia of Genes and Genomes Pathway,KEGG Pathway)是一个手工绘制出这些信号转导网络图的集合。通过KEGG Pathway,本文可以把处于同一个信号通路的基因聚集起来,验证处于同一信号通路中,相互调控的基因变异间因果关系的存在性。
1.3 贝叶斯网
贝叶斯网是一类概率图模型。该模型借助一个有向无环图,表示一系列的随机变量X1,X2,…,Xn及其相互之间的依赖关系,其中每个节点代表一个随机变量,并对应一个概率分布表。图模型直观地反映了各个随机变量之间的依赖关系,而联合概率分布表则具体量化了随机变量之间的概率依赖强度。贝叶斯网如图1所示,全部随机变量的联合概率分布可通过这些随机变量的边缘概率分布和条件概率分布相乘而得到,记为:
(1)
式中:Pa(Xi)为Xi的父节点集。
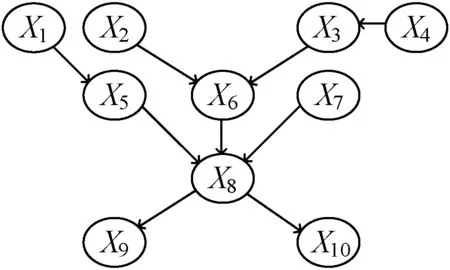
图1 贝叶斯网模型
2 数据处理
2.1 数据描述
实验所用的SNPs数据由英国WTCCC(Wellcome Trust Case Control Consortium)机构提供,本文所使用的数据是多种复杂疾病整合到一起的数据文件,共有16 179个样本,每个样本含有394 747个SNPs的变异情况。表1选取了其中两个SNPs的染色体位点和主次等位基因等基本属性的信息,部分SNPs变异情况如表2所示。

表1 每个SNP的染色体位点及其基本属性

表2 部分SNPs变异数据
表2列出了数据集中3个样本的3个SNPs情况,每一列为一个SNP的变异情况,如表2中的rs2980300_T,这是一个命名为rs2980300的SNPs,其后缀“_T”代表该SNP位点突变为次等位基因T;0、1、2三个取值分别代表样本1在该SNP位点上没有发生突变,样本2有1条染色体上的该SNP位点突变为此等位基因T,样本3则2条染色体全都发生了突变。
2.2 SNPs数据编码为基因数据
通过NCBI可以查询到rs命名的SNPs是否位于基因区域、属于哪一个基因。根据基因和SNPs为一对多的关系,SNPs数据可以编码成基因粒度,编码方式如表3所示,394 747个SNPs中有3个位于基因51150区域。
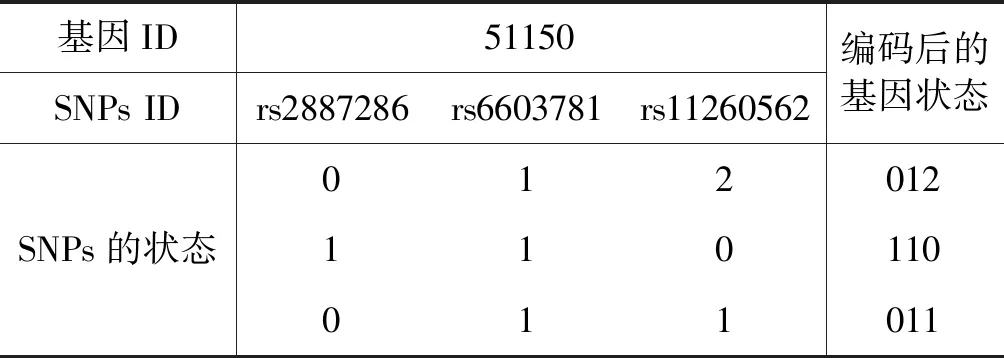
表3 基因51150的编码情况表
3 基于IPC算法的基因变异因果关系发现
3.1 IPC算法框架
基于所得的离散型基因变异数据构建贝叶斯网模型,如果检测到一个基因变量的父子(Parents and Children,PC)节点,则可以推断出调控网络中直接相互作用的基因。通过条件独立性检验构造局部因果结构,可以检测出贝叶斯网中基因变量的PC节点[17-19]。受贝叶斯半监督方法(Bayesian Semi-Supervised method,BASSUM)[17]中采用PC算法检测变量间因果关系思想的启发,本节提出一种改进的PC算法,即IPC算法(Improved-PC),检测同一信号通路中基因变异间相互作用的因果关系。
记PC(T)为目标基因T的PC节点集。由贝叶斯网性质可知,PC(T)是导致基因T发生变异的直接原因或由基因T变异导致的直接结果的集合,即PC(T)中所有基因变量跟T都是不独立的。记vi为跟基因T直接相互作用的基因,由此可得vi∈PC(T)的一个必要条件:vi跟T不满足相互独立。根据此条件,在检测目标基因T的PC节点时,遍历PC(T)的候选基因集合C(T),如果属于C(T)的基因ci与T不相互独立,则更新PC(T),使得PC(T)=PC(T)∪ci,这里ci∈C(T)。由于上述条件是vi∈PC(T)的必要条件,据此检测所得的结果很可能会引入一些非直接相互作用的基因,得到的是PC(T)的一个超集,故检测结束后需剔除掉非直接相互作用的基因。
先对超集中的非直接相互作用的基因分析。图2所示的PC(T)超集包含了非直接相互作用的基因fi,基因fi发生变异是目标基因T发生变异的间接原因,检测时如果基因fi被误加入PC(T)中,那么从贝叶斯网络结构上看,节点fi就不可能跟节点T直接连接。同时,由于根据必要条件检测所得的集合是真实PC(T)的超集,故fi跟T必然被PC(T)所d-分隔,从而在给定PC(T)的条件下,fi跟T条件独立,其中PC(T)可以通过遍历超集的幂集搜索获得。此分析过程对目标基因T变异的间接结果同样适用。

图2 根据必要条件检测到的PC(T)超集
类似地,如果基因vi属于真实PC(T),则基因vi跟目标基因T直接相互作用,故与fi情况相反,基因vi和目标基因T不会被任何集合所d-分隔,即不存在条件集合使vi跟T满足条件独立。根据vi和fi在条件独立性上的差异,可以把超集中的非直接相互作用的基因fi和属于真实的PC(T)基因vi分辨出来。
根据以上分析,可以得到IPC算法步骤如算法1所示。
算法1IPC算法
输入:包含所有变量的集合V、目标变量T
输出:PC(T)
1. 初始化:PC(T)=∅,C(T)=V-{T};
2.FORvi∈C(T)-PC(T)DO;
//遍历;
3.g(vi)=G2(vi,T);
//构造基因vi和
//目标基因T的
//G2统计量
//如果G2统计量落在拒绝域中,
//说明基因vi和目标基因T
//不满足相互独立
5.PC(T)=PC(T)∪vi;
6.ENDIF
7.ENDFOR
//通过条件独立性检验删除冗余信息
8.FORfi∈PC(T)DO
9.IF∃S⊂PC(T)-{fi},fi⊥T|STHEN
10.PC(T)=PC(T)-{fi};
//遍历PC(T)减去fi后的幂集,以此
//作为条件进行条件独立性检验
11.ENDIF
12.ENDFOR
IPC算法检测到基因的PC节点后,需要通过因果结构的识别来判定PC基因之间的因果方向。由于直接确定两个相互连接的PC节点间的方向比较困难,因此,本文通过对三个节点的基本有向无环结构进行识别,进而判断其中的父节点(Parent)和子节点(Child)。三个节点构成的基本结构包括图3的4种情况。
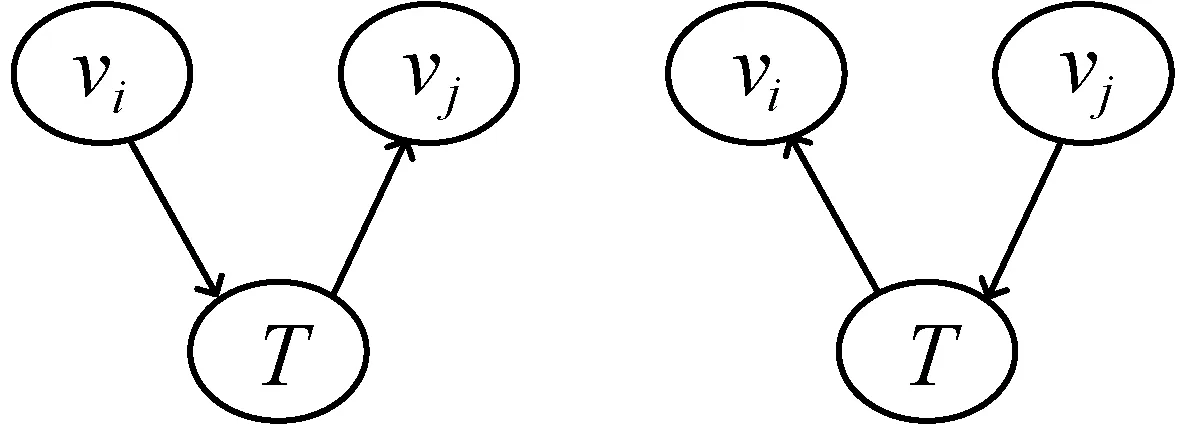
(a) 顺连 (b) 顺连
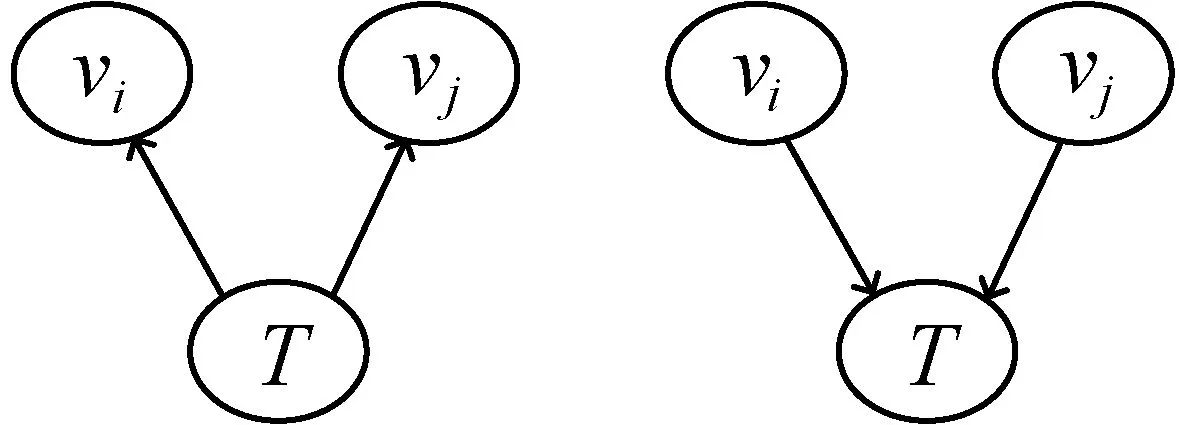
(c) 分连 (d) 汇连图3 三个节点构成的基本结构
这4种情况可以从独立性和条件独立性上的差异来实现结构的识别。情况(a)-(c)中,节点vi和节点vj并不满足相互独立,而在给定节点T这一条件下,节点vi和节点vj满足条件独立。这三种结构在独立性和条件独立性的性质上等价,无法进行有效区分,但情况(d)会呈现出相反的性质。
情况(d)属于汇连结构。该结构跟前面三种结构的区别在于,在节点T未知的情况下,节点vi和节点vj满足相互独立,但在给定节点T的条件下,节点vi和节点vj不满足条件独立。这跟前面三种结构的性质相反。因此,利用汇连结构在条件独立性上的特性,本文可以通过算法2识别出三节点构成的汇连结构,推断其中的父亲节点和孩子节点。
记从节点vi出发,到节点T终止的有向边为
算法2汇连结构识别算法
输入:目标变量T、T的PC节点集PC(T)
输出:包含目标变量T的有向边集E
1. 初始化:E=∅;
2.FORvi,vj∈PC(T)DO
3.IFvi⊥vjANDNOTvi⊥vj|TTHEN
4.E=E∪{
5.ENDIF
6.ENDFOR
不同于一般的相关性分析,在目标变量T和PC节点集PC(T)中,算法2基于条件独立性检验,先有效识别出变量中的汇连结构,进而推断出该结构中的因果方向,保证了检测得到的因果关系的可靠性。
3.2 独立性检验
本文所采用的独立性检验基于卡方检验实现。对一些较为复杂而庞大的数据进行独立性检验时,平方差的计算会增加卡方检验的运算量,所以可以构造G2检验统计量[20]来作为卡方统计量的代替。
可借助列联表来考察两种属性的独立性。如表4所示,Omn表示样本中属性1取值为Am且属性2取值为Bn的观察计数。其中M为属性1的取值数目,N为属性2的取值数目。
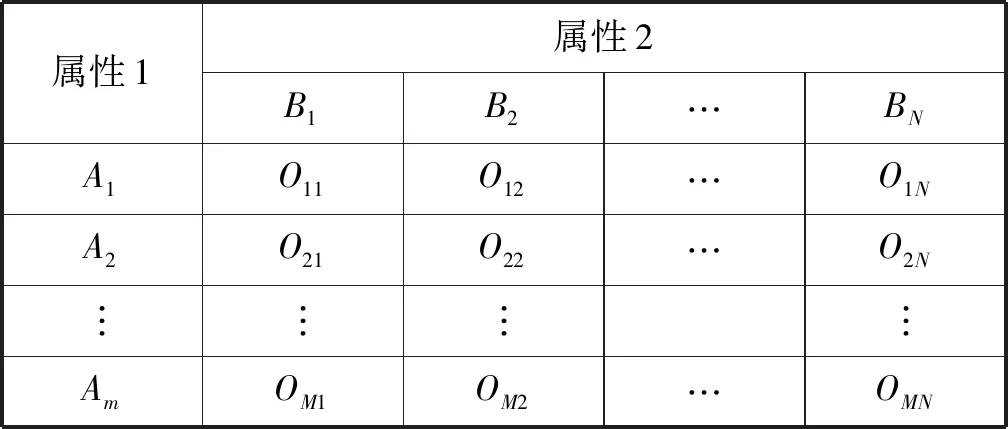
表4 M×N列联表
如果零假设“属性1和属性2相互独立”成立,则两者的联合分布率等于边缘分布率之积。故联合分布率的极大似然估计为:
(2)
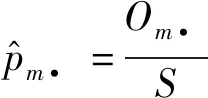
由零假设和式(1)可知,样本数据中属性1取值为m且属性2取值为n的期望样本量为:
(3)
而在备择假设中,两属性的联合分布率为:
(4)
类似地,在进行条件独立性检验时,如果在给定属性3取值为l的条件下,检验属性1和属性2是否相互独立时,对数据中满足给定属性3的取值l的样本构造属性1和属性2的列联表,由以上推导可得期望样本量为:
(5)
式中:各项的右上标l代表给定条件属性的取值为l。
在M×N列联表中,任意单元格中的观察样本数都对应着唯一一个期望样本数,为了便于记录,这里把M×N个单元格的观察样本数记为O1,O2,…,OM×N,期望样本数则对应为E1,E2,…,EM×N。于是可以得到G2检验统计量作为卡方检验的近似估计,表示为:
(6)
另一方面是自由度的计算。对每个列联表的G2检验统计量其所对应的自由度df(degrees of freedom)为:
df=(M-1)×(N-1)
(7)
在给定条件属性时,自由度为:
df=(M-1)×(N-1)×S(Con)
(8)
式中:S(Con)表示条件属性值的数目。
4 实 验
4.1 实验方案
要验证同一信号通路中相互调控的基因,其变异间具有因果关系这一假设,需要通过IPC算法检测出具有因果关系的基因对,并将该实验结果分别跟真实信号通路中相互调控的基因对进行匹配。本次实验的卡方独立性检验显著性水平设为0.01。
4.2 实验结果分析
本文使用了KEGG Pathway的真实信号通路数据来评估实验结果。为了评估实验结果的匹配程度和IPC算法的性能,本文使用召回率R(Recall)、准确率P(Precision)和F1值(F1-sorce)来评价实验效果。三者的定义如下:
(9)
(10)
(11)
式中:TP代表IPC算法检测出来的基因变异对和真实信号通路网络结构中相互调控的基因对匹配的数目;FN是真实信号通路网络结构中含有而IPC算法没有检测出的基因变异对的数目;FP为IPC算法检测出而真实信号通路网络结构中没有出现的基因变异对的数目。
根据上述指标,最后得到的实验结果与真实信号通路的对比效果如图4所示。
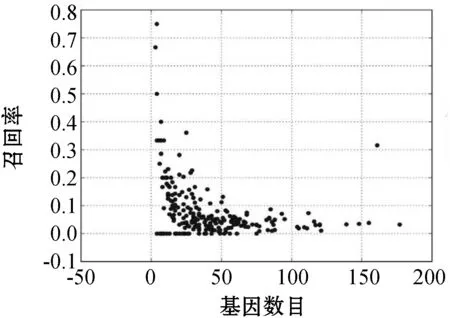
(a) 召回率
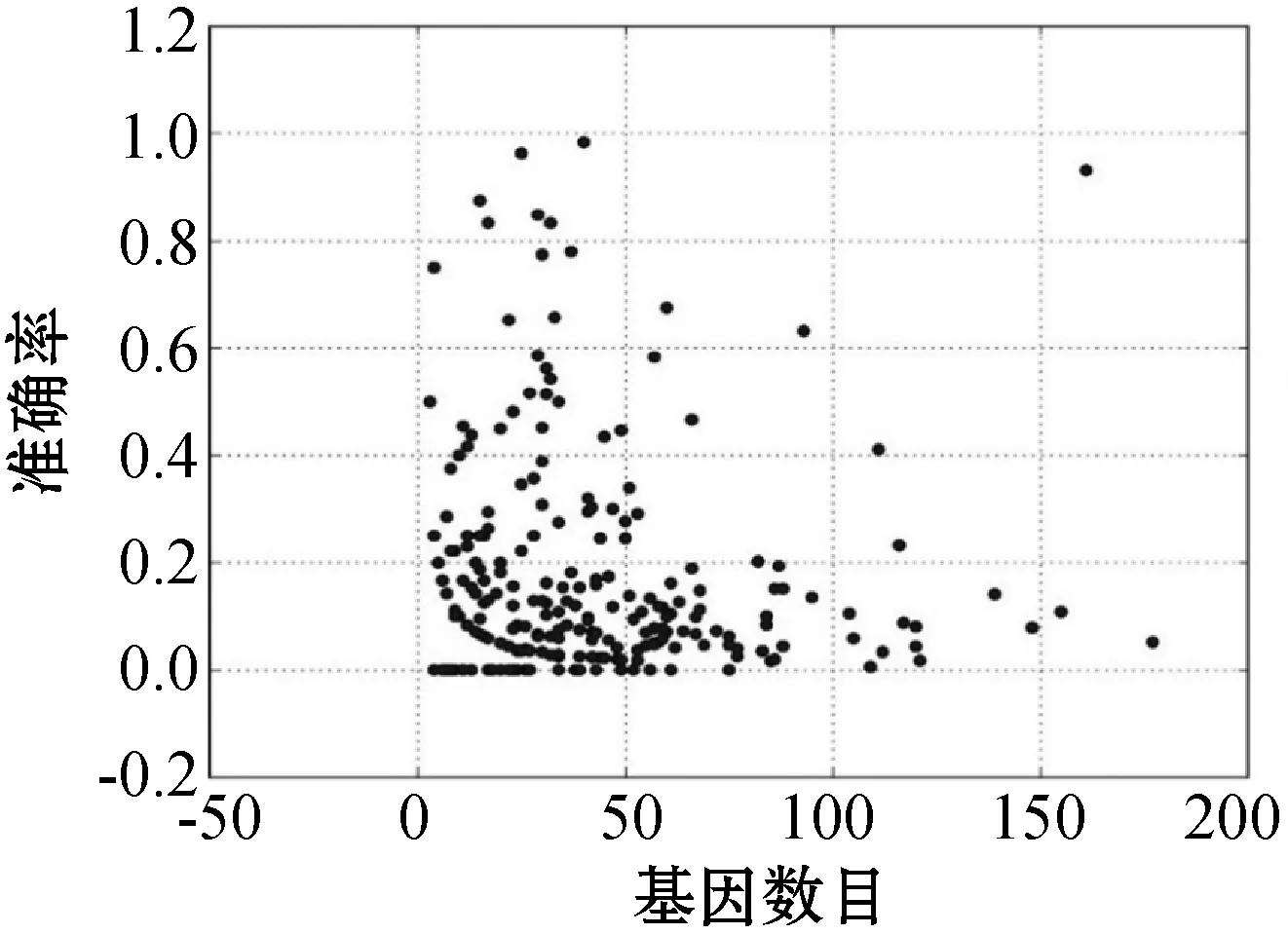
(b) 准确率
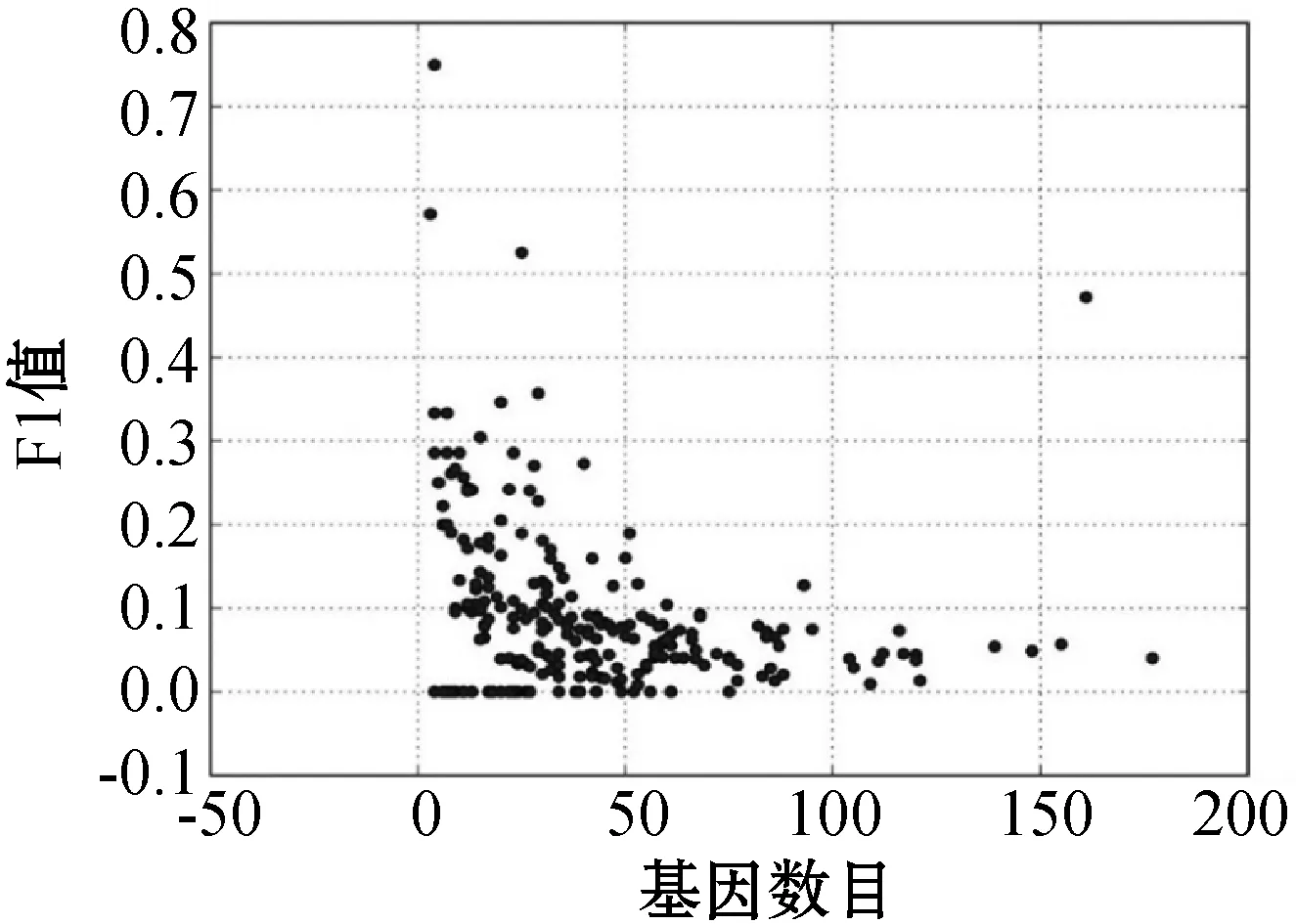
(c) F1值图4 实验检测结果跟真实信号通路网络结构的匹配评分
可以看出,算法的部分检测结果与真实信号通路中相互调控的基因对相匹配,准确率比较理想,其中某个包含161个基因的信号通路中,其准确率达到90%以上。该实验结果表明,部分相互调控的基因之间的变异具有一定的因果关系。
为了进一步验证这种匹配的非偶然性和IPC算法的有效性,本文进一步进行了随机对照实验作为对比实验。实验保持真实信号通路的拓扑结构不变,将同一信号通路中的所有节点所对应的基因标签随机混淆,信号通路中原有的调控信息破坏掉,并以随机信息替换,得到了随机对照的网络结构。结果发现其中并没有基因对可以与IPC算法结果相匹配,部分实验结果如表5所示。这一结果验证了这种匹配的非偶然性,基因变异间的因果关系跟信号通路中的基因调控关系存在某种关联。

表5 本文IPC算法实验、LD算法对比实验和随机对照实验的指标对比

续表5
在图4中一个具有161个基因的信号通路,其召回率、准确率和F1值都突然明显升高,其中原因可能跟信号通路的类型有关。进一步分析,基因数目超过10个的信号通路共有181个,总体情况如表6所示。其中,细胞过程和环境信息处理这两类信号通路的平均基因数较多,其平均准确率也偏低;遗传信息处理类型的信号通路只有4个,代表性较弱;人类疾病和生物体系统这两类的平均基因数都在48左右,然而平均准确率分别是0.11和0.18,相差较大,可能还有其他因素本实验中没有考虑到;实验效果比较理想的是新陈代谢类型的信号通路,相较于人类疾病和生物体系统类型,虽然其平均基因数较少,但平均准确率增幅很大,达到0.38,且样本量有40,具有一定的代表性。这也说明了对于某些信号通路,通过本文算法可以有效地检测出其基因变异间所蕴含的因果关系。

表6 基因数超过10个的信号通路的情况
表7给出了部分跟真实信号通路网络结构相匹配的IPC算法检测结果,调控类型列中ECrel代表酶与酶的催化逐次反应,PPrel代表该基因对的相互作用表现为蛋白质与蛋白质的相互作用。

表7 检测基因变异的因果关系所验证到的基因的调控情况
5 结 语
本文研究了相互调控的基因之间的变异的因果关系。把WTCCC研究机构的SNPs数据编码为基因粒度的数据,并使用因果关系发现IPC算法检测出了数据中的因果关系。将检测结果分别跟KEGG Pathway的真实信号通路网络结构数据和随机对照实验网络结构对比,发现因果结构在部分真实信号通路网络中获得了验证,而跟基于连锁不平衡的对比实验则体现了IPC算法具备更良好的性能。

