转运限制下的冷藏集装箱多式联运路径优化
刘 松 邵毅明 彭 勇
1(重庆交通大学交通运输学院 重庆 400074)2(山地城市交通系统与安全实验室 重庆 400074)
0 引 言
冷藏集装箱多式联运起步较晚,2016年3月,大连港创新冷藏集装箱多式联运,相关温度指标等才达国际标准[1]。随着“一带一路”倡议,中新战略性互联互通项目的深入实施和人们生活水平的不断提高,跨国贸易更加频繁,东盟、欧洲的水果和乳制品等冷藏品不断通过冷藏集装箱进行运输,冷藏集装箱多式联运需求越来越大。2017年商务部发布的《商贸物流发展“十三五”规划》指出要鼓励应用专业冷藏运输、推动冷链物流发展。同年,交通运输部发布的《交通运输部等十八个部门关于进一步鼓励开展多式联运工作的通知》提出加快多式联运发展,构建高效顺畅的多式联运系统。
多式联运由多种运输方式构成,相较于单一运输方式,还需要考虑不同运输方式之间的转运以及铁路、水路运输发班时刻表等的影响,使其运输路径选择比单一运输方式下的路径选择更为困难,近年来引起了学者的广泛关注。卢欣等[2]对带时间窗约束的多式联运路径选择问题进行了研究。张燕等[3]考虑运输费用和运输时间对海铁联运进行了研究。雷定猷等[4]以最小运输时间、里程与费用为目标函数,以线路限界、桥梁承载能力、起重设备的起重能力为约束条件,建立了长大货物多式联运路径优化模型,并设计了求解算法。Assadipour等[5]综合考虑运输成本和风险,对危险品公铁联运进行了研究。吕学伟等[6]从低碳的角度研究了多式联运最优路径选择问题。曹欢等[7]考虑决策者风险规避程度对危险品公铁联运路径选择进行了研究。李珺等[8]对速度服从随机分布时的绿色多式联运路径优化问题进行了研究。赵志文等[9]研究了危险品多式联运路径优化问题。于雪峤等[10]从运量不确定视角,建立了以总费用为目标的多式联运路径优化模型。刘杰等[11]研究了以运输总成本和碳排放为目标的多式联运路径优化问题。甄远迪等[12]研究了运输时间和碳排放量不确定下的多目标多式联运路径优化,并设计了粒子群算法。姬晓岭等[13]研究了地下集装箱的多式联运问题。成耀荣等[14]从多式联运经营人的角度,建立考虑碳排放的多任务多式联运路径优化模型,并设计了算法。万杰等[15]考虑运输成本、时间和物流服务质量研究了多目标多式联运路径选择问题。李萍等[16]以总成本和风险为目标研究了由多个路径期组成的危险品公铁联运网络扩张问题。
已有文献对普通货物、危险品及长大货物多式联运路径选择问题进行了研究。由于冷藏集装箱多式联运起步较晚,对冷藏集装箱多式联运路径选择问题研究较少,而冷藏集装箱多式联运和前文所述的危险品、长大货物多式联运路径选择问题类似,相较于普通集装箱运输有其自身的运输特点,还需要考虑如制冷费用、运输时限以及为减少货损货差通常会限制冷藏集装箱在运输过程中不同运输方式之间的转运次数等特点对优化结果的影响。刘璘等[17]研究了以制冷成本、运输成本、转运成本在内的总成本最小为目标的冷藏集装箱海铁联运运输路径优化,但没有考虑实际多式联运中铁路、水路等运输方式发班时刻对路径优化的影响。由于受发班时刻的影响,冷藏集装箱运输所需的时间和费用与出发时刻有很大的关系,将导致运输成本呈现出动态变化的特征。不同出发时刻所需的出行时间不同,出行费用也不同,从而得到的优化路径不同。
另外,由于冷藏集装箱运输还需要考虑货损货差,时效性要求高,通常货主会对转运次数限制和运抵目的地有时间窗要求,而该问题又是典型的NP(Non-deterministic Polynomial)难题[18],对该类问题的求解一直以来都受到学者的高度关注。Assadipour等[19]设计了启发式算法求解多式联运路径问题。刘帅等[20]设计了动态规划法求解随机时变路网环境下的运输路径选择问题。
综上所述,现有文献中少有同时考虑实际冷藏集装箱多式联运中铁路、水路等运输方式发班时刻对路径优化的影响以及货主对转运次数的限制和时间窗要求。基于此,本文针对该问题建立以运输费用、中转费用和冷藏费用最少为目标的优化模型,并针对所求问题的NP难特点设计求解算法。该算法具有一定的理论意义及实际应用价值。
1 问题描述与建模
1.1 问题描述
在如图1所示的多式联运网络示意图中,现需要将冷藏集装箱由起点1运输到终点7,其中,铁路和水路运输方式按照发班时刻表发班,多式联运托运人对冷藏集装箱有转运次数限制和到达目的地时间窗要求,求以运输成本、转运成本和冷藏成本最低为目标的运输路径。

图1 多式联运示意图
1.2 模型建立
1) 参数定义:
V—多式联运网络节点集合i,j∈V;
M—运输方式集合,m,n∈M;
E—所有边的集合;
s—货物运输的起点;
d—货物运输的终点;
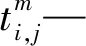

c—冷藏集装箱的单位冷藏费用;
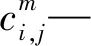

G—转运次数上限值;

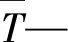
to—货物离开起点的时刻;
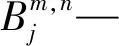


2) 决策变量:
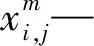

3) 目标函数及约束条件:
(1) 目标函数。冷藏集装箱多式联运过程产生的费用主要包括运输成本、转运成本以及冷藏成本。因此,目标函数如下:
(1)
式(1)共包含三部分。第一部分表示货物的运输成本;第二部分为不同运输方式间的转运成本;第三部分为货物的冷藏成本。
(2) 约束条件。流量守恒约束,即起点净流量为1,终点净流量为-1,其他节点流量守恒。
(2)
集装箱在相邻两节点间进行运输时,只能选择一种运输方式:
(3)
运输的连续性约束:
(4)
到达目的地的时间限制:
(5)
冷藏集装箱运输须满足转运次数限制:
(6)
决策变量只能取整数0或者1:
(7)
(8)
集装箱在节点处只能转运一次:
(9)
变量非负约束:
(10)
2 问题求解
针对所求问题的NP难特点,本文设计遗传算法进行求解。
2.1 编码与初始种群的生成
2.1.1编 码
由于最短路径经过的节点无法提前知道,路径具有变长的情况,因此染色体长度应是不固定的,本文采用可变长的路径编码方法。针对多式联运网络节点间有多种运输方式的特点,对染色体分两段编码,前一段为路径节点,后一段为节点间的运输方式。如图2所示,染色体的路径节点部分p=(1,3,6,7),表示图1中从节点1到节点7的一条路径。在交叉、变异操作时,把第二段运输方式插入第一段的空隙中。图2中,H表示公路,R表示铁路运输,W表示水路运输。
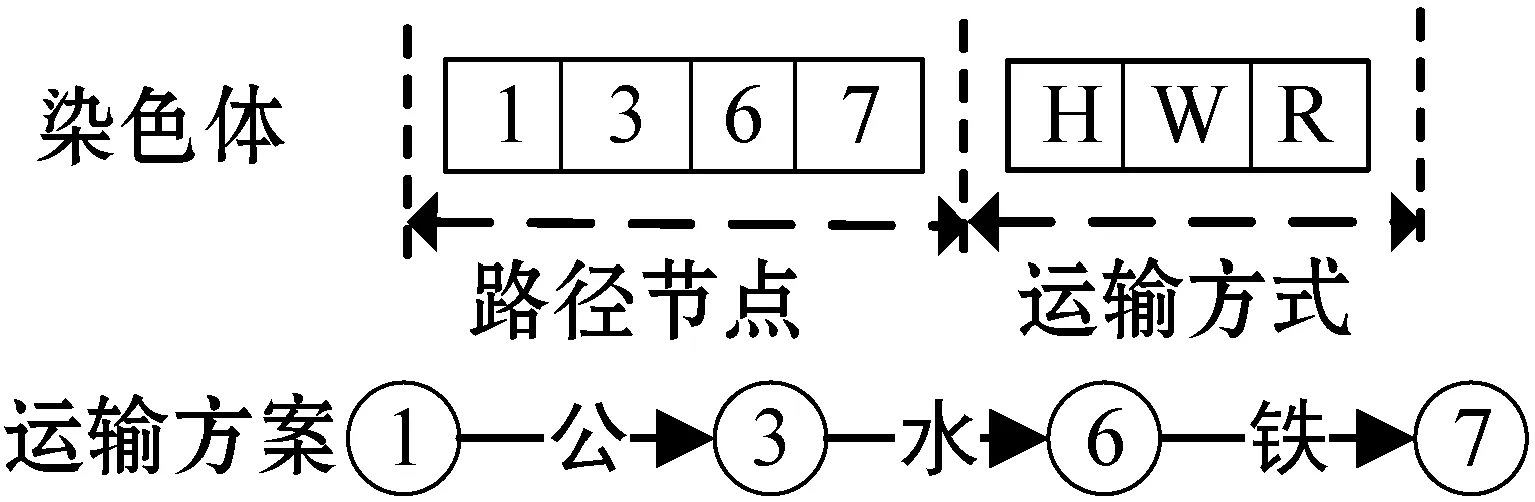
图2 染色体编码
2.1.2初始种群的生成
本文利用如下方法生成初始种群:
步骤1由多式联运网络生成连通矩阵,即两点间只要存在一种运输方式连通,则表示连通,矩阵边的权值取各连通运输方式边的权值的最小值。
步骤2利用动态规划法生成染色体的第一段编码,然后随机选择节点间的运输方式生成第二段编码,得到一条初始染色体。
步骤3若种群数量已达要求,则终止;否则随机生成0~1之间的小数乘以该路径各弧段的权值,并更新多式联运网络权值,返回步骤2。
2.2 适应度评估与约束条件判断
采用目标函数的倒数为适应度函数F:
F=Z-1
(11)
优化模型包括转运次数不超过要求的最多运行转运次数和时间窗要求,但在算法的进化中,有些个体的转运次数和时间窗会超过要求。因此,采取以下方法进行调整:
1) 求个体的总转运次数和运输总时间;
2) 判断每个个体所示方案的转运次数或者运输总时间是否超过要求,若超过,则以一定的概率删除;
3) 如果有q个个体被删除,就在余下群体中随机复制q个个体。
2.3 遗传操作
步骤1选择。采用轮盘赌策略进行选择操作。
步骤2交叉。本文对染色体的第一段路径节点部分采用两点交叉法来进行交叉操作。另外,交叉操作中可能会产生非法个体,采取以下方法对非法染色体进行修复。
第一个交叉节点到起点可能存在没有通路的情况,如果没有连通,则利用动态规划法寻找第一个交叉节点与相邻的上一节点的有效路径替代,如无法找到有效路径,则查找再上一节点,如此往复直到找到有连通的路径为止。同样地,第二个交叉节点到终点可能存在没有通路的情况,如果没有连通,则利用动态规划法寻找第二个交叉节点与相邻的下一节点的有效路径替代,如无法找到有效路径,则查找再下一节点,如此往复直到找到有连通的路径为止。
另外,需要注意的是,交叉后可能会出现环路,即在路径编码中出现了相同的节点,若出现环路,则删除环路,去除环路中间节点,保留一个相同节点。如图3所示的染色体,其中节点3出现了两次,形成了闭环,则去掉环,得新的节点1、3、6、7。完善上述操作后,对于未发生变化的基因片段,保留其第二段编码中的运输方式,对于染色体第一段编码发生变化的基因片段,随机选择节点间的运输方式生成对应的第二段编码。

图3 环路处理
步骤3变异。本文采用改进的散射变异方法进行变异操作,给多式联运网络弧段随机赋值,利用动态规划法生成染色体的第一段节点编码。然后随机选择节点间的运输方式生成第二段编码,进而得到变异后的染色体,并采用式(12)调整变异概率,在迭代后期增强种群的最优解搜索能力。
(12)
式中:I为迭代次数。
2.4 精英保留与终止策略
采用精英保留策略进行全局最优解更新。采用最大迭代次数作为终止条件,算法求解流程如图4所示。
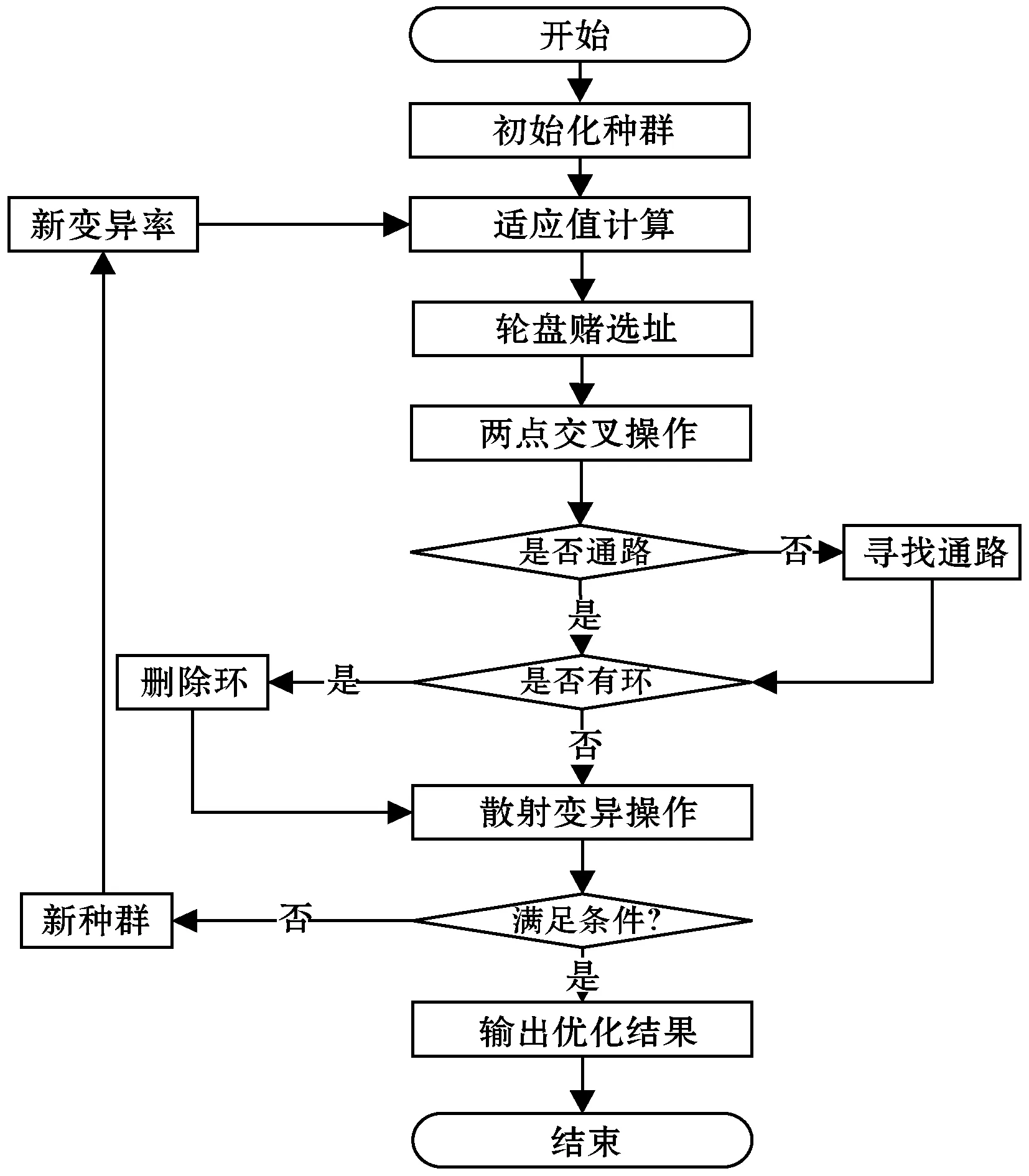
图4 遗传算法求解流程
3 算例设计与结果分析
3.1 算例设计
为验证模型和算法的有效性,采用前期研究[21]的网络,如图5所示。以节点1为起点,节点25为终点,由于班期限制下的冷藏集装箱多式联运路径优化问题是一个相对较新的问题,没有标准的测试实例库,需要自己构造测试数据。构造数据的方法一般有两种,一种是随机,另一种是在已有实例上修改。本文在Solomon[22]实例基础上修改得到,选取Solomon中R101的前25个点依次对应图5中的节点,并将Solomon中节点间的欧几里得距离扩大10倍(km)。不同运输方式之间的转运时间及转运成本如表1所示,各种运输方式的运输速度、运输成本以及发班时间如表2所示。冷藏集装箱的冷藏成本为12元/h,设现需要将冷藏集装箱在07:30由起点1出发运输到终点25,要求最多转运5次,并在50 h内到达目的地,求所需总成本最低的运输方案。
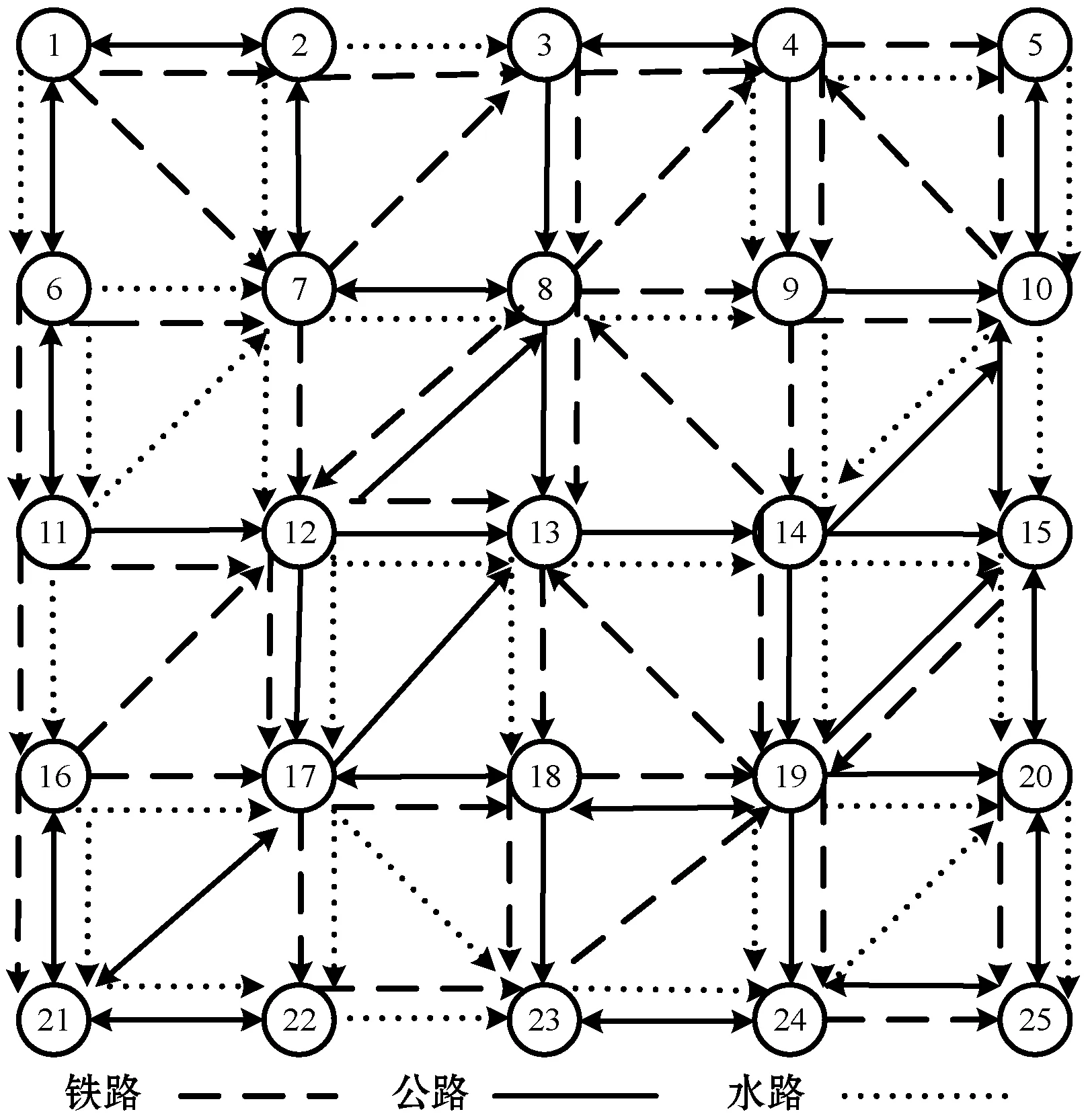
图5 多式联运网络
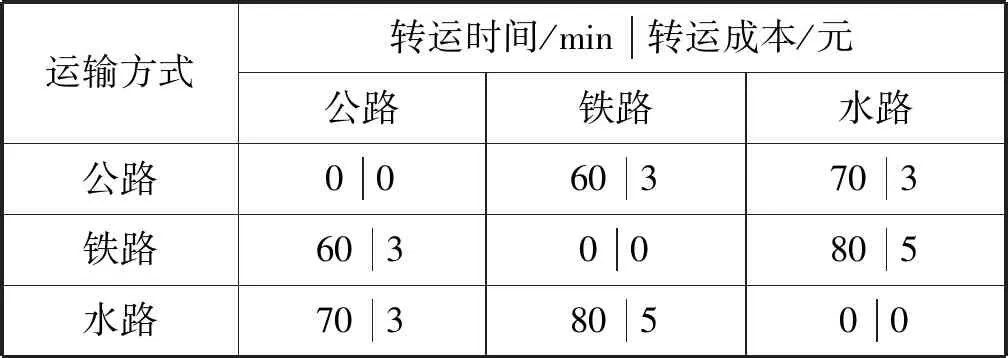
表1 不同运输方式之间的转运时间和成本

表2 各运输方式的运输速度、成本及班期
3.2 结果分析
设置种群规模为300,交叉概率为0.8,变异概率为0.5,最大进化代数为100,采用MATLAB 2014a编程实现算法,运行平台为Intel(R)Core (TM)i5-6300U 2.40 GHz CPU 4.0 G内存。运行程序35 s后获得最优解。算法求解进化过程如图6所示,适应值逐步减小,最后收敛,算法在达到一定迭代次数后稳定在最优解保持不变。

图6 目标函数求解进化过程
所需总运输成本为4 081元,所需要的运输时间为2 640 min,即44 h,共需中转5次,满足中转次数和到达时间窗要求。具体运输方案如下:

冷藏集装箱从节点1出发后,通过水路运输到节点6,转铁路运输到节点7并继续通过铁路到达节点12,转公路到达节点17转铁路到达节点22后继续通过铁路到达节点23,转公路运输到节点24后,转水路运输到达终点。
为了验证本文所建模型和算法的有效性,引入蚁群算法进行对比,使用设计的遗传算法与蚁群算法在不同迭代次数条件下的求解结果如表3所示。可以看出,蚁群算法和遗传算法都能够在有限迭代次数限制条件下求出满意解,其中遗传算法所求得的满意解比蚁群算法更低。

表3 遗传算法与蚁群算法成本比较
4 结 语
考虑转运次数限制和铁路、水路运输方式具有发车时间限制以及到达时间限制特点下的冷藏集装箱多式联运对于减少货损货差、降低运输成本具有重要意义。本文构建了运输总成本最少的优化模型,不仅考虑了运输费用和节点换装费用,还考虑了受铁路、水路发班时间限制影响而波动较大的冷藏费用以及转运次数限制。实验结果表明,该算法收敛性较好,能有效求解该问题。

