基于神经网络观测器的容错控制技术研究
荆家玮,王 伟,牛智奇,赵良玉*
(1. 北京理工大学宇航学院,北京 100081; 2. 西安现代控制技术研究所,西安 710065)
0 引 言
随着现代战场环境日益复杂多变,对飞行器控制系统的性能及可靠性提出了新的要求。控制系统中传感器、导航系统、控制器、执行机构等的故障率以及对故障的处理能力直接决定了飞行器可靠性的高低。因此,当飞行器在飞行过程中遇到突发故障时,不但应使之能够继续飞行,同时还应兼顾一定的飞行任务,这对控制系统的故障诊断与容错控制能力提出了新的挑战。
1971年,NIEDERLINSKI提出了完整性控制[1]。以此为标志,容错控制的概念开始被广泛引入各种控制系统中。时至今日,已经涌现出诸多先进的容错控制技术并广泛应用于各类飞行器,尤其在新型先进飞行器的设计研究中,取得了令人瞩目的研究成果。经典容错控制按照系统故障和冗余方式的不同分为被动容错控制和主动容错控制[2]。其中,通过故障检测与诊断获取故障信息进而实现系统重构的主动容错控制,具有更强大的故障处理能力。因此,基于解析冗余的动态系统故障诊断和主动容错控制已成为航空航天领域中急待攻克的技术难题之一。
目前,逐渐发展出针对执行机构故障进行补偿的自适应控制技术,以应对未知类型的执行机构故障[3-5]。其中,在考虑系统参数不确定性和扰动因素的情况下,自适应故障补偿设计方法中的鲁棒性问题成为研究的重点[6]。神经网络由于在自适应性、在线学习和非线性映射等方面能力出众,同时还具备一定的鲁棒性和容错能力,受到研究人员的青睐[7-9]。本文针对执行机构不同的故障类型,研究了基于神经网络观测器的鲁棒自适应容错补偿控制器设计方法。神经网络观测器实现故障估计与状态观测,通过设计鲁棒自适应容错控制器自动补偿执行机构的故障和参数不确定性。理论分析与数值仿真均表明,所提出的方案可以确保自适应闭环系统的解一致有界,且状态参数一致收敛。
1 执行机构的故障模型
本文以制导火箭为研究对象,火箭弹的运动学和动力学模型可以通过小扰动假设及“系数冻结法”化简为用以下状态空间形式表示的线性模型[8]。

(1)
式中:A是火箭弹的状态矩阵,也是固有特性矩阵;B是输入矩阵;C是输出矩阵;u(t)是舵面的控制信号;ΔA(t)代表模型内的时变参数不确定性,且满足式(2)的条件。
ΔA(t)=BW(t)
(2)
式中:W(t)是未知矩阵,满足‖W(t)‖≤l*,l*是一个未知常数。
舵面是制导火箭弹调整位置和姿态的执行机构。本文考虑舵面失效、舵面卡死两种故障类型。令ui(t)代表第i个舵面的控制输入信号,usi(t)代表第i个舵面卡死位置处的未知有界信号,扩展到系统中表示为us。uiout(t)是舵机的实际输出信号。在第i个舵面故障时,实际的舵机输出可以表示为
uiout(t)=ρiui(t)+σiusi(t),i=1,2,…,m
(3)
式中:ρi、σi用于表示某一舵面的故障类型和程度,系统中为对角矩阵的形式,即ρ=diag(ρ1,ρ2,...,ρm),σ=diag(σ1,σ2,...,σm)。
式(3)可表示某一舵面的3种工作情况:①当ρi∈(0,1)且σi=0时,uiout(t)=ρiui(t),表示舵面的部分失效故障;②当ρi=0且σi≠0时,ρi=0表示舵面的实际输出已完全不受控制输入ui(t)的影响,此时舵面卡死在未知有界时变函数usi(t)处[9];③当ρi=1且σi=0时,舵面工作正常。由此,舵面故障下的系统状态方程式(1)可写为
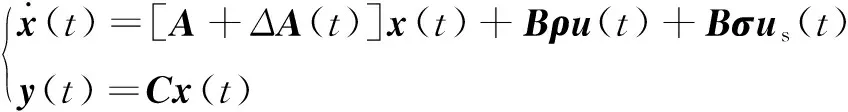
(4)
为方便下文的控制器设计,做出以下假设[5]:
假设1:对任何舵面故障类型,ρ∈{ρ1,ρ2,…ρm},且所有{A,Bρ}均是一致可控的。
假设3:对任何舵面故障类型,ρ∈{ρ1,ρ2,…ρm},rank[Bρ]=rank[B]。
假设4:在m-1个舵面发生卡死故障之前,其余舵面仍可使得系统达到所需的控制目标。并且,所有舵面可以同时遭受部分失效故障的影响。
基于假设1可知,{A,B}是稳定可控的,所以一定存在一个定常矩阵K∈m×n和一个正定矩阵P∈n×n满足以下条件:
(A+BK)TP+P(A+BK)<0
(5)
进一步分析可以得到,假设3保证矩阵B中列的线性组合可以由矩阵Bρ重构,即存在一个矩阵K1满足
(A+BρK1)TP+P(A+BρK1)<0
(6)
通过式(5)~(6)可以选择一个足够大的正实数ε满足
(7)
基于假设1~4,本文将构造一个鲁棒自适应状态反馈控制器,使得闭环系统的解是一致有界的。即使在舵面故障和参数不确定性同时存在,且对系统动力学产生一定影响的情况下,状态参数能够逐渐收敛。
2 故障估计与容错控制律设计
2.1 自适应容错补偿控制律设计

(8)

(9)

将式(8)代入式(4),得到闭环系统方程

(10)
由假设4可知,式(3)中的对角阵ρ不能为零,所以存在一个正常数μ满足
‖xTPBρBTPx‖>μ‖xTPB‖2
(11)
由假设2可知,存在一个正常数kc满足
‖σus(t)‖≤μkc
(12)
不失一般性,引入kd=l*2/μ,其中l*是式(2)中W(t)的下界。需要说明的是这里的参数μ、kc、kd均是未知的。
辅助控制量Ka(t)和Kb(t)的表达式为
(13)
(14)

(15)

(16)
(17)
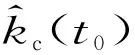
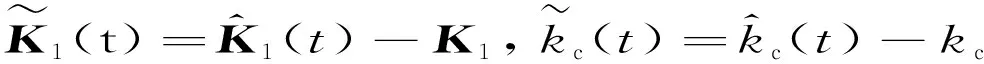
(18)
(19)
(20)

(21)
证明:根据式(10)的自适应闭环系统,首先选取式(22)所示的Lyapunov函数。

(22)
根据式(18)~(20),结合式(11)~(12)两个不等式条件,可以得到V对t(t>0)求导结果为
(23)
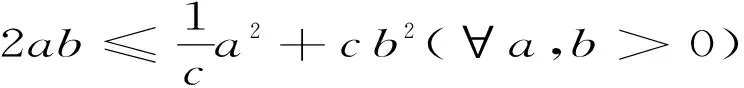
对于不等式(23),定义-Q=1/εI+(A+BρK1)TP+P(A+BρK1),经过一系列推导,得到
(24)
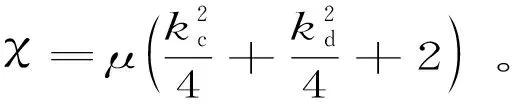
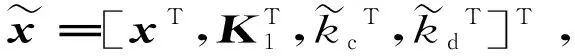

(25)
然后
(26)
从而可以说明式(10)的自适应闭环系统和式(18)~(20)的误差系统是一致有界的。同时可以推导得
(27)

2.2 神经网络观测器设计
前文中介绍了基于状态反馈的容错控制律设计,但在实际工程中,系统状态参数不易测量,由此提出观测器的概念来辅助状态反馈的实现。此外,神经网络在故障诊断方面具备逼近任意连续有界非线性函数的能力[11],在建立故障非线性模型的基础上,能够对故障程度进行良好估计。因此,本节提出通过径向基函数(radial basis function,RBF)神经网络观测器进行故障估计与状态观测,来辅助前文容错算法的设计,从而形成如图1所示的基于神经网络观测器的故障估计与容错控制系统。
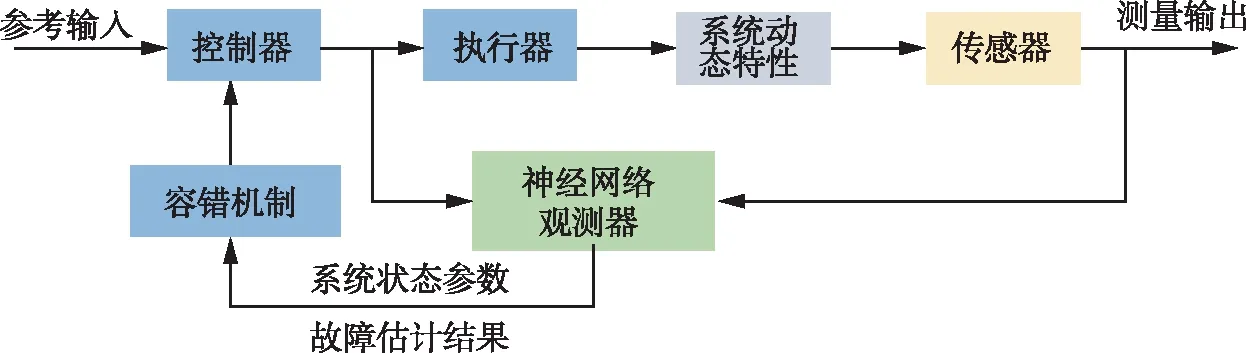
图1 故障估计与容错控制系统示意图Fig.1 Schematic of fault estimation and fault-tolerant control system
针对式(1)所描述系统可设计如式(28)所示的RBF神经网络观测器。
(28)

在式(28)所示的观测器中,未知非线性函数采用理想权值W*和足够数量的基函数h(x)组成的神经网络逼近。
(29)

设计自适应神经网络控制律为[12]
(30)

3 案例分析
本文以某型制导火箭弹为研究对象,火箭弹的运动方程组可分为纵向运动和侧向运动。在纵向运动方程中,以俯仰角速率、攻角和俯仰角为状态参数;侧向运动方程中,以侧滑角和偏航角速率为状态参数。在考虑系统内部参数不确定性的条件下,主要针对舵面控制性能失效和舵面卡死(定值卡死和时变位置卡死)这2类故障类型进行弹体纵向运动和侧向运动的仿真分析。纵向运动和侧向运动容错控制系统的初始条件和仿真参数如表1所示。

表1 容错控制系统的初始条件和仿真参数Tab.1 Initial conditions and simulation parameters of the fault-tolerant control system
3.1 火箭弹舵面控制性能失效仿真
情形1:考虑0.9 s处俯仰舵发生60%失效故障,即舵面偏转产生的力矩大小为正常情况下的40%。神经网络观测器对失效率的估计情况如图2所示,故障发生后实际攻角αs对期望攻角αd的跟踪情况如图3所示。

图2 情形1下神经网络观测器的估计Fig.2 Estimation curve of neural network observer in case 1

图3 情形1下攻角跟踪曲线Fig.3 Angle of attack tracking curve in case 1
由图2可以看出神经网络观测器能够对舵面控制性能失效率快速准确地进行估计。图3表明本文所提出的容错方案能够在舵面失效的情况下保证实际攻角对期望攻角的有效跟踪。
3.2 火箭弹舵面固定位置卡死仿真
情形2:考虑在2 s处偏航舵发生时长为1.5 s卡死故障,卡死在8°位置。偏航方向的状态参数侧滑角β和偏航角速率ωy的仿真曲线如图4所示,容错控制器的自适应参数K1曲线如图5所示。

图4 情形2下的状态参数曲线Fig.4 State parameter curve in case 2

图5 情形2下控制参数K1估计值变化曲线Fig.5 Estimated value of control parameter K1 in case 2
图4说明容错控制律在舵机定值卡死的故障情况下能够保证飞行状态稳定。图5可以看出容错控制律中的自适应参数在故障调节过程中一致有界。
3.3 火箭弹舵面时变位置卡死仿真
情形3:考虑在5 s处俯仰舵发生时长为5.5 s卡死故障,卡死位置为0.05sin(3t)rad。神经网络观测器对故障发生的时变位置估计见图6。俯仰方向状态参数俯仰角速率ωz、攻角α和俯仰角ϑ的真实值与估计值曲线如图7~9所示。容错控制器自适应参数K1曲线如图10所示。

图6 情形3下神经网络观测器的估计Fig.6 Estimation curve of neural network observer in case 3

图7 情形3下状态参数ωz的真实值与估计值Fig.7 Real and estimated values of state parameter ωz in case 3

图8 情形3下状态参数α的真实值与估计值Fig.8 Real and estimated values of state parameter α in case 3

图9 情形3下状态参数ϑ的真实值与估计值Fig.9 Real and estimated values of state parameter ϑ in case 3

图10 情形3下控制参数K1估计值的变化曲线Fig.10 Estimated value of control parameter K1 in case 3
图6~9表明神经网络观测器能够实时准确地估计舵面卡死位置信息以及俯仰角速率、攻角和俯仰角3种系统状态参数。图10表明在故障调节过程中,容错控制器自适应估算的控制参数也在有界范围内变化,并随着故障的消除归于定值。
从以上仿真分析可以看出,当火箭弹某一舵面出现一定程度的控制性能损失或非持续性卡死的情况时,容错控制器通过自适应地调节控制参数大小,可补偿故障和模型内不确定性带来的干扰。该方法最终保证了各状态参数的快速有界收敛,且对其具有实时观测的能力。研究成果对于解决实际工程问题具有一定的理论指导意义。
4 结束语
本文研究了一类考虑参数不确定性条件下的火箭弹故障估计与鲁棒自适应容错控制问题。针对执行机构部分失效、定值和时变位置处卡死等常见的故障类型,提出了一种有效的基于神经网络观测器的故障估计方法以及自适应容错补偿控制器设计方案。通过对某型火箭弹进行纵向运动和侧向运动下舵面不同失效程度和卡死情况的仿真,证明了本文所提出的基于神经网络观测器的容错控制方案能够快速准确地对故障程度和系统状态实施估计并保持飞行状态收敛稳定,数值仿真结果证明了所提算法对故障处理的有效性和鲁棒性。

