萨德导弹拦截防御作战弹道设计与仿真分析

雍恩米，赵良玉，赵 暾

(1. 中国空气动力研究与发展中心，四川 绵阳 621000；2. 北京理工大学 宇航学院，北京 100081)

0 引 言

萨德导弹系统全称为末段高空区域防御系统(terminal high altitude area defense, THAAD)，是美国现有防空反导装备体系的重要组成部分[1]。萨德导弹系统采用卫星、雷达、红外三位一体综合预警方式，其拦截高度如图1所示[2]，其作战拦截高度处于“爱国者”反导系统和“宙斯盾”反导系统之间，号称是“当今世界唯一有能力在大气层内和大气层外拦截弹道导弹的地基系统”。鉴于萨德导弹系统强大的制空能力和所配属AN/TPY-2型X波段雷达强大的窥视能力，美国自其服役之日起就致力于萨德系统的全球部署策略，目前已在包括美国本土、关岛、韩国等在内的多个地方部署[3]，德国、日本等地也在部署计划之中。随着高超声速技术的逐渐成熟和高超声速武器时代的来临[4]，美国对基本型萨德导弹系统还在进行升级。

由于萨德导弹系统强大的反导能力，其作战过程和拦截弹道也一直是包括俄罗斯、中国在内的多个军事强国的重点关注对象[5]。

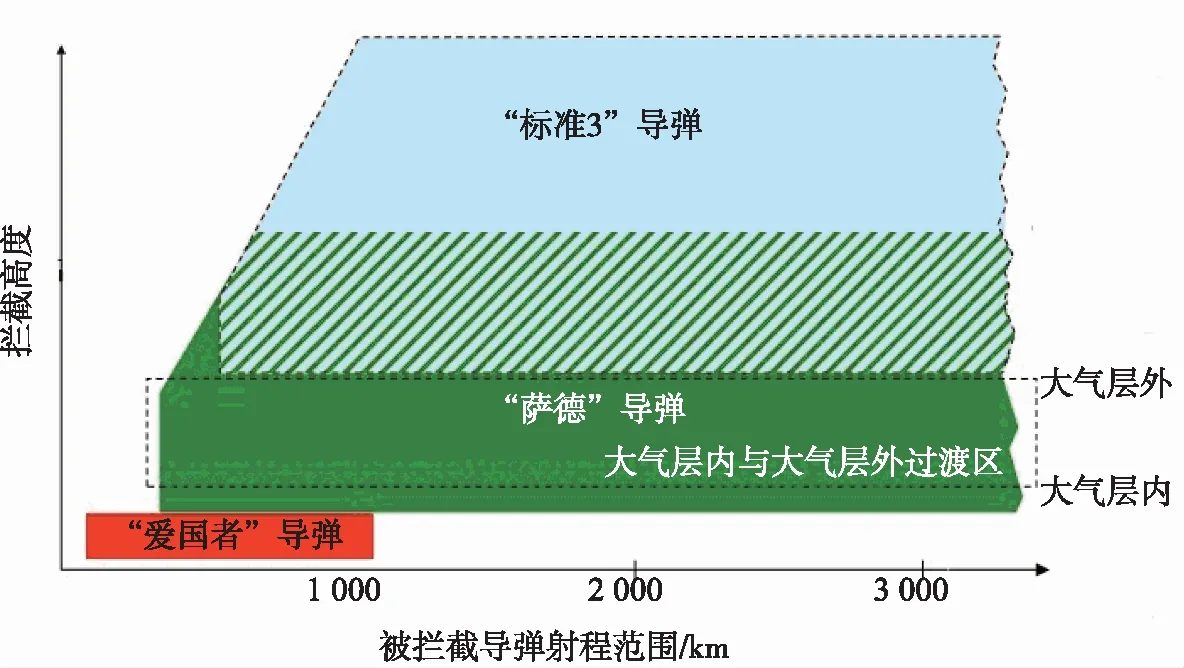
图1 萨德导弹拦截高度示意图Fig.1 Interception altitude of THAAD missile

本文在分析萨德导弹系统作战过程的基础上，结合从公开资料获取的萨德导弹几何参数，基于Missile DATCOM工程计算软件预测其气动特性，并开展末制导段前的拦截弹道的数学仿真计算，对萨德导弹的作战性能进行了定性与定量分析。

1 萨德导弹系统作战过程

根据公开报道的多次飞行试验结果分析可知，萨德导弹系统的主要作战过程如下[6- 7]：

1) 预警：反导预警系统对来袭弹道导弹进行全程预警，即地面站通过国防支援计划 (defense support program, DSP)系列和天基红外系统 (space-based infrared system，SBIRS)系列导弹预警卫星侦测到来袭的弹道导弹发射后，迅速通报陆基远程预警雷达、萨德系统的AN/TPT-2等雷达装备，待雷达捕捉到弹道导弹目标后，由地面站整编形成实时、准确、要素齐全、理解一致的反导预警情报，并分发给美军反导拦截系统。

2) 探测：根据预警情报，萨德导弹系统配属的AN/TPT-2X波段雷达对威胁目标进行轨迹探测、分类、识别、判定并确定类型，也可根据需要来预测目标的发射点和碰撞点。雷达探测信息可用于战场环境威胁评估、武器分配，并向反导作战指挥部门发布信息。

3) 威胁评估：威胁评估包括确定对设防区域或优先保护资源造成威胁的敌方导弹类型，受到威胁的具体设防对象以及攻击每个设防对象的敌方导弹数量。

4) 武器分配：指挥控制系统根据来袭的导弹类型，选择可用的发射车和拦截导弹，确定战场区域、最佳发射窗口和可能的拦截时间段。根据来袭导弹类型及数目确定所需的拦截次数和拦截导弹数量，再根据可能的拦截点位置预测拦截导弹发射时间。

5) 交战控制：交战控制主要包括确定火控方案、进行杀伤评估和可能的二次拦截任务。在拦截导弹发射之前，“萨德”导弹系统确定最终的弹道控制方案和发射窗口，安排雷达和通信支撑资源。在拦截导弹发出以后，战术掩蔽小组确定来袭导弹信息并通过雷达将其传给拦截导弹。在拦截过程中，雷达跟踪导弹和目标，并将杀伤评估数据提供给战术掩蔽小组。在拦截失败的情况下，如果战场条件允许，指控系统会发出再次拦截指令。在不能确定有效杀伤的情况下，系统重新识别目标，再次执行威胁评估及武器分配任务。

2 萨德导弹主要参数

萨德导弹外形类似火箭弹，采用轴对称无翼设计，主要包括尖锥形头部、圆柱形助推器和尾部可收缩的稳定裙。根据公开资料，通常认为萨德导弹的主要参数如表1所示，其基本外形和尺寸如图2所示[8]。

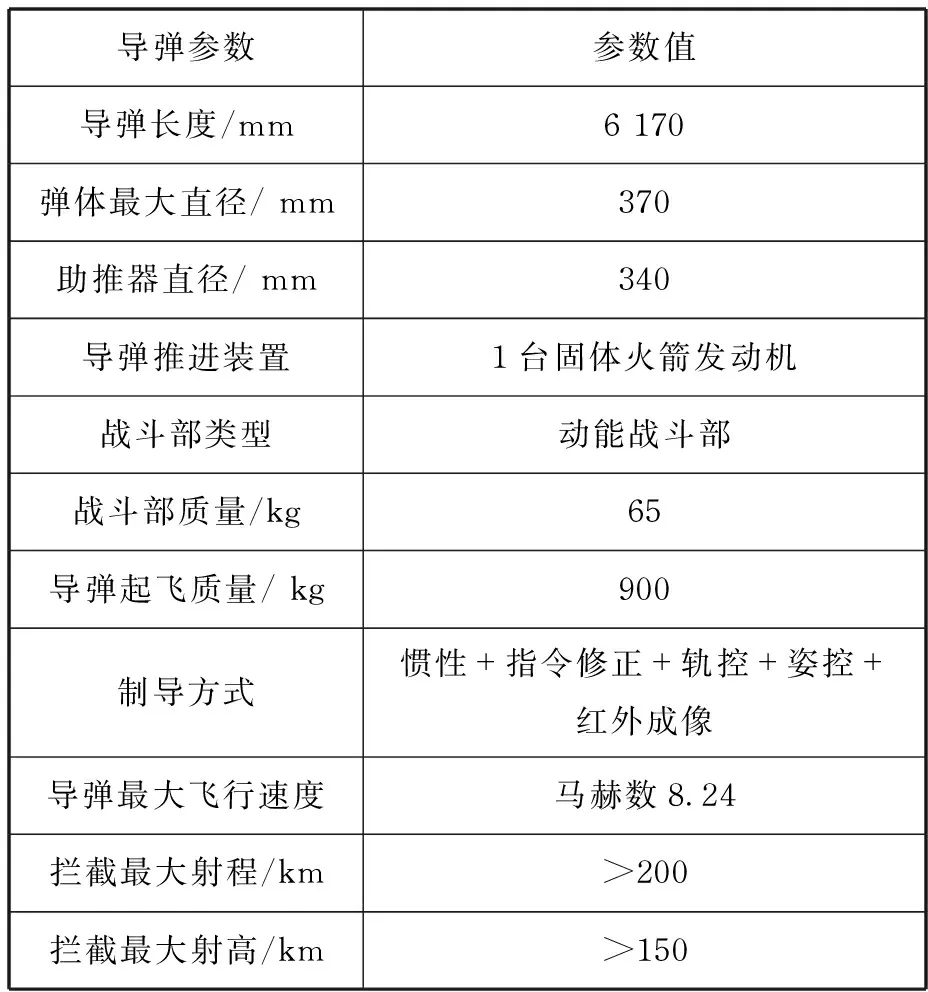
表1 萨德导弹主要参数Tab.1 Main parameters of THAAD missile

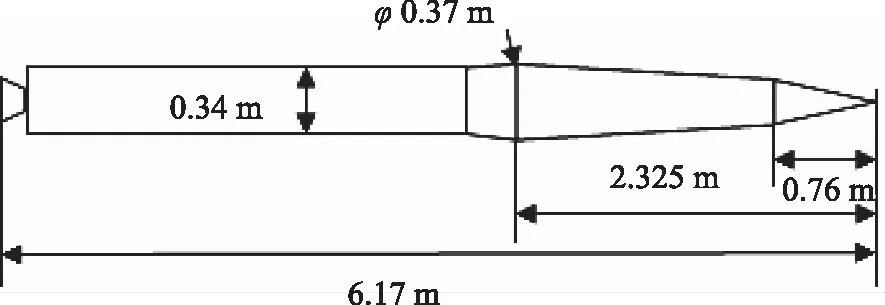
图2 萨德导弹外形参数Fig.2 Configuration parameters of THAAD missile

依据图2所示的“萨德”导弹几何参数，可采用气动力工程估算软件Missile DATCOM预测其气动特性，并作为下文弹道仿真所需的气动数据。固体火箭发动机是“萨德”导弹最重要的组成部分之一，它的性能参数基本上决定了导弹的作战性能。通过分析其几何参数及公开报道的相关资料，取固体火箭发动机的性能参数如下：

1) 助推器直径340 mm，包括燃烧室、喷管和级间连接裙在内的总长度为3 800 mm，燃烧室壳体采用碳纤维缠绕材质，装药长度3 380 mm；

2) 采用固体含量为87%的丁羟推进剂；

3) 导弹主动飞行17 s左右，最大速度约2 800 m/s；

4) 为提高火箭发动机总冲，取装药的体积装填因子η=0.9，喷管面积比为9；

5) 为保证发动机不产生较严重烧蚀，取发动机喉通比(喷喉面积/装药通道面积)为0.45。

基于上述性能参数，给出萨德导弹固体火箭发动机的推力参数如表2所示。

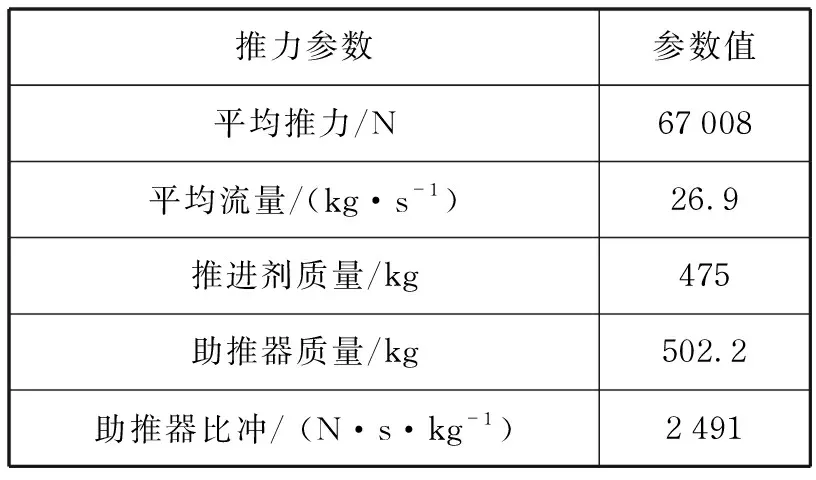
表2 萨德导弹推力参数Tab.2 Thrust parameters of THAAD missile

3 萨德导弹拦截弹道设计

3.1 拦截导弹弹道设计流程

拦截导弹弹道设计的主要任务是根据给定的拦截导弹发射点及雷达测得的目标弹道参数，预测进攻弹道并确定控制拦截导弹飞行的弹道基本参数。对于主要性能参数确定的拦截导弹，确定拦截弹道即计算基本发射诸元，包括发射时刻、程序角设计变量(亚音速段最大攻角)以及发射方位角等[9]。

考虑到拦截导弹攻击的是空间活动目标，如果目标运动规律已知，如假设进攻弹道导弹按弹道式轨迹飞行，可以首先根据拦截导弹的拦截高程和射程范围预测目标运动轨迹中的可拦截区域，将攻击活动目标的发射诸元计算问题转换为攻击预测拦截点的诸元计算问题，并生成拦截弹道[10]。根据以上思路，给出拦截导弹的弹道设计步骤如下：

1) 初始化：给出拦截导弹发射点位置参数，根据雷达测得的进攻导弹飞行参数和运动模型预测其进攻弹道。

2) 计算预测命中点：根据拦截导弹的射程能力，即高程-射程曲线计算一组进攻导弹运动轨迹中可能的拦截点，即预测命中点。

3) 迭代计算发射诸元：以每一个预测命中点为目标，依次迭代计算地基拦截导弹的发射方位角A0和程序转弯角中的最大攻角αmax。

4) 保存发射诸元：如果迭代成功，且满足约束条件，保存发射诸元参数；否则，对进攻导弹弹道再次进行预测，计算下一组预测命中点，重新计算发射诸元。

由此可得萨德导弹系统的拦截弹道设计流程如图3所示。

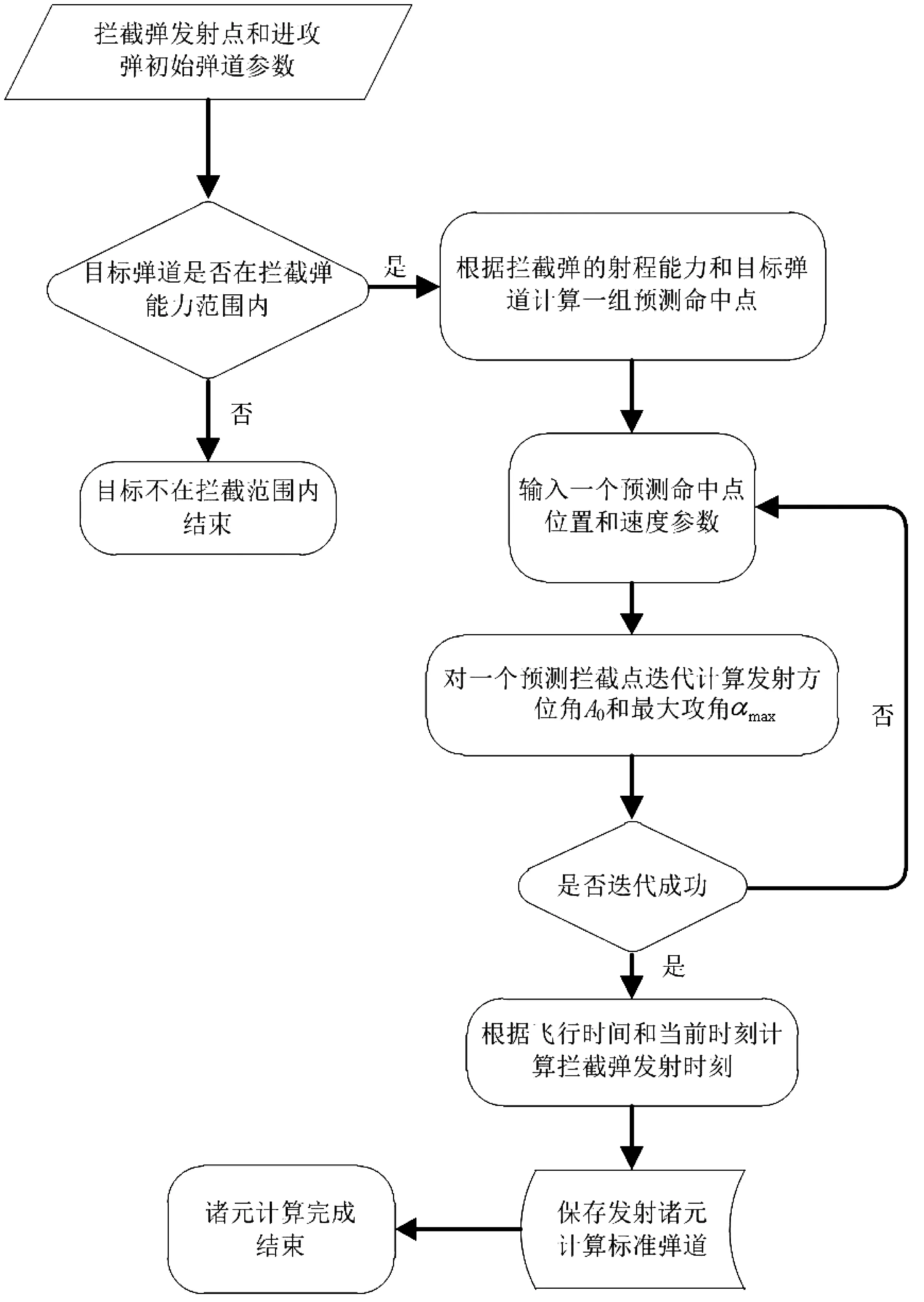
图3 拦截弹道设计流程Fig.3 Flow chart of interception trajectory design

3.2 拦截导弹发射诸元计算方法

1) 牛顿法迭代计算A0和αmax

当给定一个发射点和预测命中点时，首先确定发射方位角A0和程序角设计变量αmax，使拦截导弹飞行到与预测命中点的同样高度时，与预测命中点的纵向偏差ΔL和横向偏差ΔB小于允许误差。

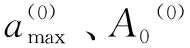
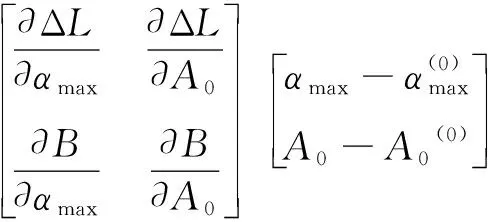
(1)

同时考虑函数关系A0=A0(ΔL,ΔB)，αmax=αmax(ΔL,ΔB)，将αmax,A0在(ΔL(0),ΔB(0))处线性展开可得

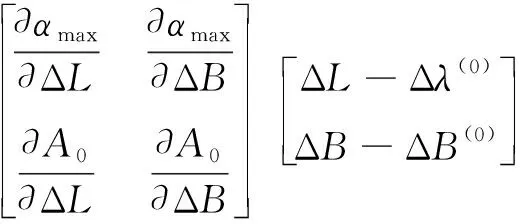
(2)

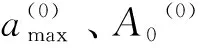
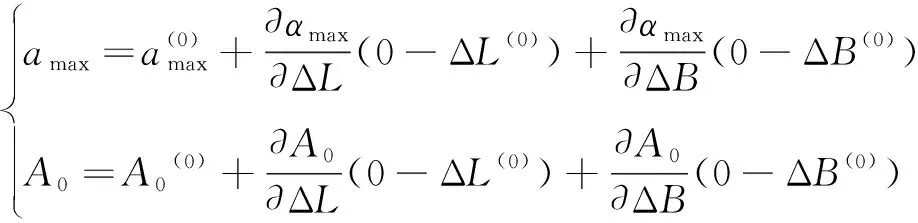
(3)

结合式(1)和式(2)可以求解需要的偏导数

(4)

由此，可以得到迭代计算发射方位角A0和亚音速段最大攻角αmax的基本步骤如下：

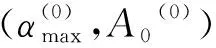
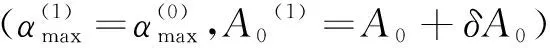
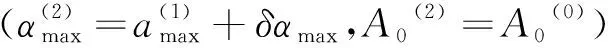
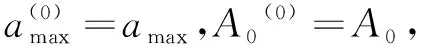
计算过程中式(4)用到的偏导数可由求差法求得。

2) 拦截弹发射时刻的确定

记进攻导弹发射时刻为t0，进攻导弹到预测命中点的时刻为tm，诸元计算得到拦截导弹飞行到预测命中点的飞行时间为tflight，则拦截弹发射时刻为

tl=tm-tflight

(5)

4 萨德导弹拦截弹道仿真

4.1 仿真条件

仿真中进攻导弹与拦截导弹初始弹道参数见表3。本文以研究拦截弹道设计为主，假设进攻导弹参数能够通过天基预警系统和地面雷达探测信息获得并预测。拦截弹道设计中的进攻导弹参数通过弹道仿真获得。进攻导弹和拦截导弹的弹道仿真积分步长均取0.1 s，导弹动力学方程见文献[9]。

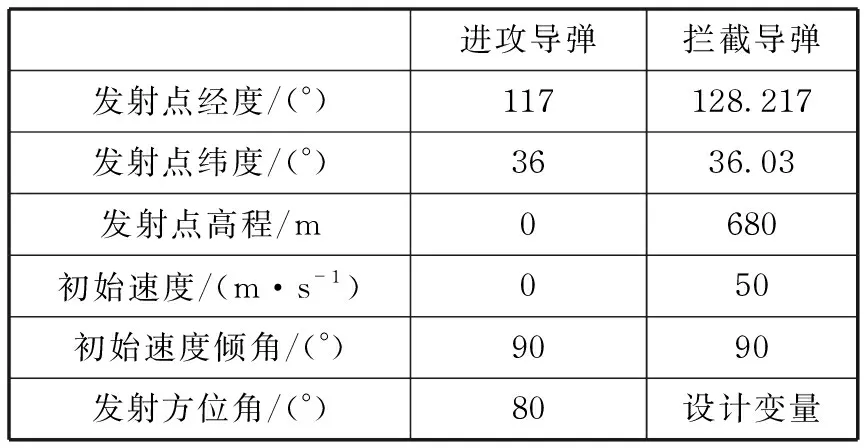
表3 仿真初始条件Tab.3 Initial conditions of simulations

4.2 仿真结果

1) 进攻导弹弹道

进攻导弹总体、气动和推进参数参照伊斯坎德尔导弹选取，其弹道仿真结果见图4，地面轨迹见图5。进攻导弹射程约为1 600 km，最大飞行高度约180 km。

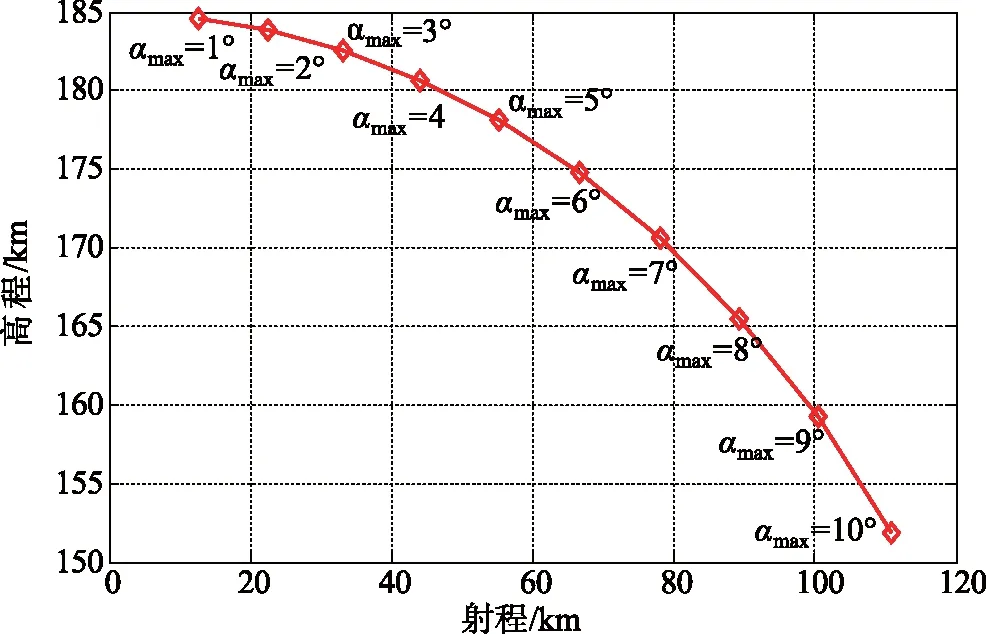
图5 进攻导弹地面轨迹Fig.5 Ground trajectory of attack missile

2) 拦截导弹弹道

拦截导弹飞行性能主要受助推段推力曲线和气动力特性等总体性能参数的影响。若拦截导弹的总体性能参数不变，则飞行程序角是决定拦截导弹飞行高程和射程的主要因素。本文的飞行程序角采用近似公式设计，弹道设计参数为亚音速段最大攻角αmax和发射方位角A0。本文中拦截导弹飞行高程是指拦截导弹飞行的最大高度，拦截射程是指拦截导弹飞行至最高点时的星下点与发射点的球面射程。因此，通过改变αmax可以得到不同的拦截导弹飞行高程和射程，确定拦截导弹的射程-高程曲线是计算预测命中点的前提。

采用前文所述的萨德导弹性能参数进行仿真计算，获得不同亚音速段最大攻角下的向上拦截情况的高程-射程曲线，如图6所示。同时，考虑向下拦截的情况，针对某一拦截高度，给出拦截弹道曲线族，如图7所示。综合仿真结果可以看出，萨德导弹的拦截射程在100 km以上，拦截最大高程接近200 km。

图6 拦截导弹高程-射程曲线Fig.6 Altitude-range curve of intercept missile

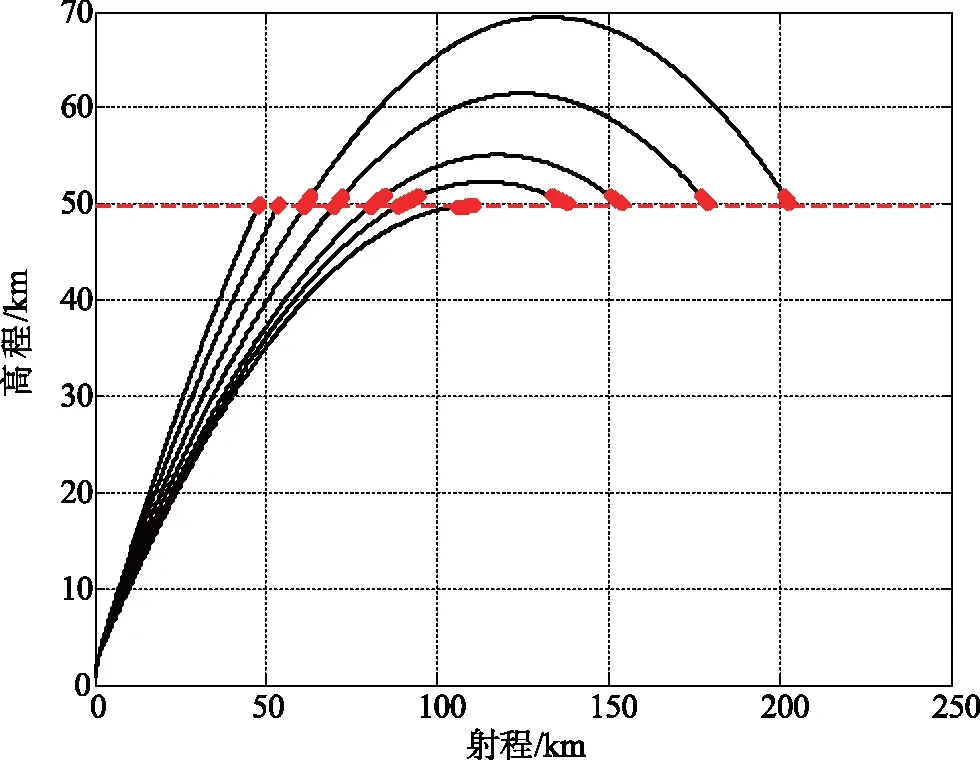
图7 萨德拦截弹道族Fig.7 Interception trajectories of THAAD

根据高程-射程曲线，给定拦截导弹发射点位置，则可以计算拦截导弹的预测命中点。通过对进攻导弹的弹道进行积分，判断每一点是否满足高程、射程约束条件，并记录一组满足条件的进攻导弹位置和速度参数作为预测命中点。本文假设在韩国部署的萨德系统位置为拦截导弹发射点，则预测命中点的仿真计算结果如图8所示。

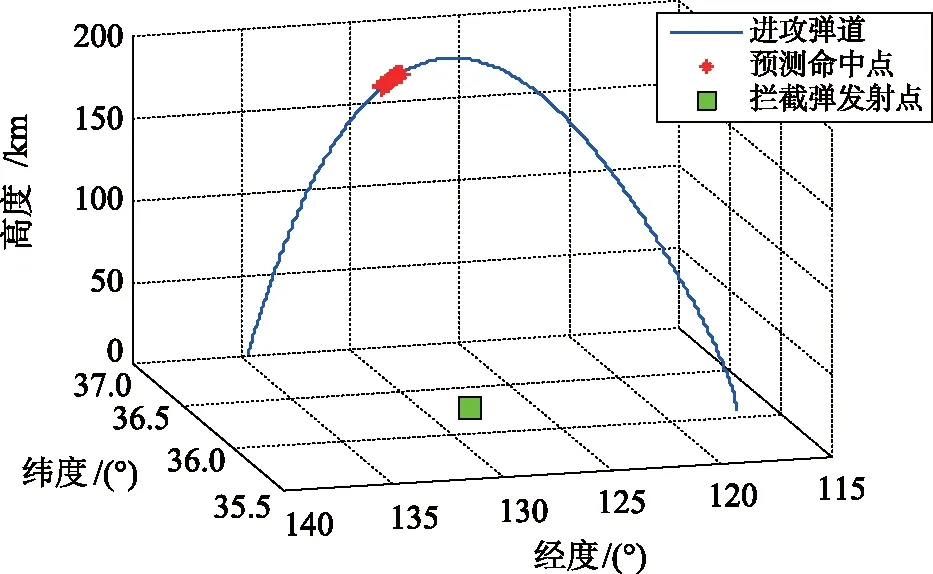
图8 预测命中点仿真计算结果Fig.8 Simulation results of predicted attack points

以各预测命中点为目标点，即可计算拦截导弹发射诸元。如果迭代成功，再根据诸元计算结果计算拦截导弹的标准弹道和发射时间，仿真计算得到的进攻与拦截弹道如图9所示。

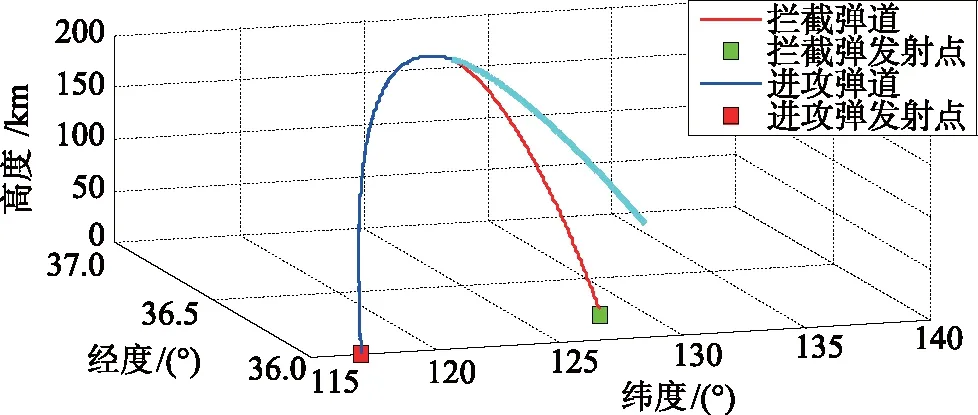
图9 进攻与拦截弹道Fig.9 Attack and intercept trajectories

最后，在STK软件环境下开展进攻与拦截弹道视景仿真，仿真结果如图10所示。其中绿色曲线为进攻弹道导弹轨迹，橙色曲线为萨德导弹拦截轨迹，两条曲线交汇点则为拦截点。

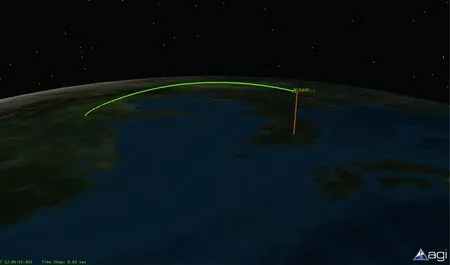
图10 进攻与拦截弹道视景仿真Fig.10 Attack and intercept trajectory scenario simulation

需要指出的是，本文设计的拦截导弹标准弹道仅为拦截导弹进入末制导段前的弹道，仿真中设置的进入末制导段的初始拦截误差小于1 km。要实现精确碰撞拦截，还需增加末制导段，相关制导律设计为下一步研究内容。

5 结束语

本文在给出萨德导弹系统作战过程和几何参数的基础上，对萨德导弹的总体性能参数进行反设计。以部署在韩国的萨德导弹系统为例，对其拦截弹道进行设计与仿真分析，获得了其作战弹道特性。下一步将开展拦截导弹末制导段的制导律设计与仿真工作，为更深入地分析萨德导弹系统的作战性能提供依据。