柱形装药接触爆炸条件下对钢筋混凝土板的毁伤规律研究

张 强，余 曜，迟德建，朱志鹏，蒋 涛

(上海机电工程研究所，上海 201109)

0 引 言

现代战争中，空面导弹打击的敌方陆上硬目标如指挥所、大中型桥梁和军事通信大楼等均由钢筋混凝土板、梁结构构建而成。用先进的侵彻弹药摧毁敌方的这些重要设施可以迅速重创敌方，掌握战争的主动权。因此，研究钢筋混凝土板、梁在爆炸载荷作用下的破坏模式和毁伤规律，对发展反硬目标先进常规战斗部技术，打赢未来高技术条件下的局部战争具有重要意义。

在常规武器弹药打击作用下，钢筋混凝土板构件的动力响应和破坏模式尤为复杂，钢筋混凝土板的破坏程度主要取决于炸药当量、边界条件、板的材料和结构参数等。目前已有不少国内外学者对钢筋混凝土板件在爆炸载荷作用下的动力响应和破坏模式开展了相应的研究[1-3]。汪维等[4]对四边固支条件下的方形钢筋混凝土板进行了不同爆炸距离作用和装药量下的数值模拟研究，得到了近场爆炸条件下方形钢筋混凝土板的破坏模式。李臻等[5]对不同直径、质量装药和爆高的23组不同钢筋混凝土π截面梁板构件的爆炸进行了试验研究，分析了其破坏模式和规律。以上研究大多是基于近场爆炸条件，将爆炸载荷近似为点源爆炸来研究钢筋混凝土板构件的毁伤机理，而对于柱形装药接触爆炸作用条件下，装药外形尺寸对板构件的动力响应和破坏模式研究较少。因此，本文基于量纲分析方法，通过数值模拟开展不同直径、长径比装药对钢筋混凝土板的动态响应进行研究，分析柱形装药对钢筋混凝土板的毁伤规律。最后，在有限元模拟数据的基础上，采用曲线拟合方法建立预测钢筋混凝土板破坏特征量的经验公式，以期为重要建筑物和防护结构的抗爆性能评估和反建筑物战斗部设计提供一定参考。

1 理论分析

爆炸冲击波对钢筋混凝土靶板的冲击毁伤研究过程涉及各物理量参数的响应规律，可通过量纲分析方法找到各参量之间的关系。对于薄板构件，贯穿破坏是影响钢筋混凝土薄板构件抗局部破坏的主要因素。因此，本文主要对TNT装药接触爆炸对钢筋混凝土板贯穿破坏的影响进行量纲分析研究。图1为柱形TNT装药与钢筋混凝土板接触作用图。其中，D为装药直径；H为装药高度；d为钢筋混凝土板的厚度；R1为爆炸载荷作用下钢筋混凝土板正面压碎区的破坏直径；R2为爆炸载荷作用下钢筋混凝土板背面震塌区的破坏直径；R0为爆炸载荷作用下钢筋混凝土板贯穿区的直径。

通过分析，影响板爆炸贯穿直径R0的参量主要有：

1) 装药参数：装药质量M，装药密度ρe，炸药的爆速vd，以及单位质量能量密度e，爆轰产物膨胀系数γ。

2) 钢筋参数：钢筋密度ρc，钢筋强度σc，钢筋的弹性模量Ec，泊松比μc；

3) 混凝土参数：初始密度ρ0，单轴抗拉强度σt，单轴抗压强度σp，配筋率ηc，弹性模量E0，泊松比μ0。

基于以上物性参数，可以得到

R0=f(M,e,ρe,γ,vd;ρc,σc,Ec,ηc，μc;ρ0,E0,μ0,σt,σp)

(1)

为了考虑装药长径比和装药直径对钢筋混凝土爆炸破坏的影响，引入两个装药几何参数：药柱直径D和药柱高度H。炸药的装药密度是个定值，因此装药质量M可以用药柱直径D和药柱高度H来表示。

(2)

这里还需引入一个特征长度量来描述无量纲贯穿直径随药柱直径之间的变化差异，即钢筋混凝土板的厚度d。文献[5]的实验中，所有板的厚度d为一个定值，约为4.2 cm。

根据以上分析，对式(1)进行改写得

R0=f(D,H,e,ρe,γ,vd;ρc,d,σc,Ec,ηc,μc;ρ0,E0,μ0,σt,σp)

(3)

得到无量纲的相似准数为

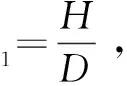
(4)

考虑到实际情况，混凝土、钢筋的材料密度等物性参数是不变的，无量纲变量∏2，∏4，…，∏13均为常量，有

∏=α·F(∏1,∏3)

(5)

即

(6)

式中：α是常数；F(·)是无量纲贯穿直径与装药几何参数之间的函数。

2 数值模拟

2.1 计算模型

参照文献[5]中的实验设置，按照装药直径为4 cm，装药质量分别为20 g、60 g的条件设计2种仿真工况，选取AUTODYN材料库中所提供的混凝土C35MPA、TNT、空气AIR和钢筋STEEL4340等材料。钢筋和混凝土单元采用分离式建模方法建模，混凝土用solid实体单元建模，钢筋采用梁单元建模，钢筋和混凝土单元共节点以拉格朗日方法来划分网格。空气和炸药采用Euler网格建模，空气和钢筋混凝土之间采用流固耦合算法。模型跨度为1 000 mm，整体外观尺寸为1 000 mm×400 mm×195 mm，混凝土和钢筋的网格尺寸均为5 mm，混凝土强度取C40，钢筋、混凝土的有限元模型见图2～3。空气域的外观尺寸为1 000 mm×150 mm×400 mm，空气单元网格尺寸为5 mm。边界条件采用梁体左右两端简支设置，空气域设置Flow-out流出边界条件，空气域的网格单元数为480 000。空气包裹下的计算模型如图4所示。

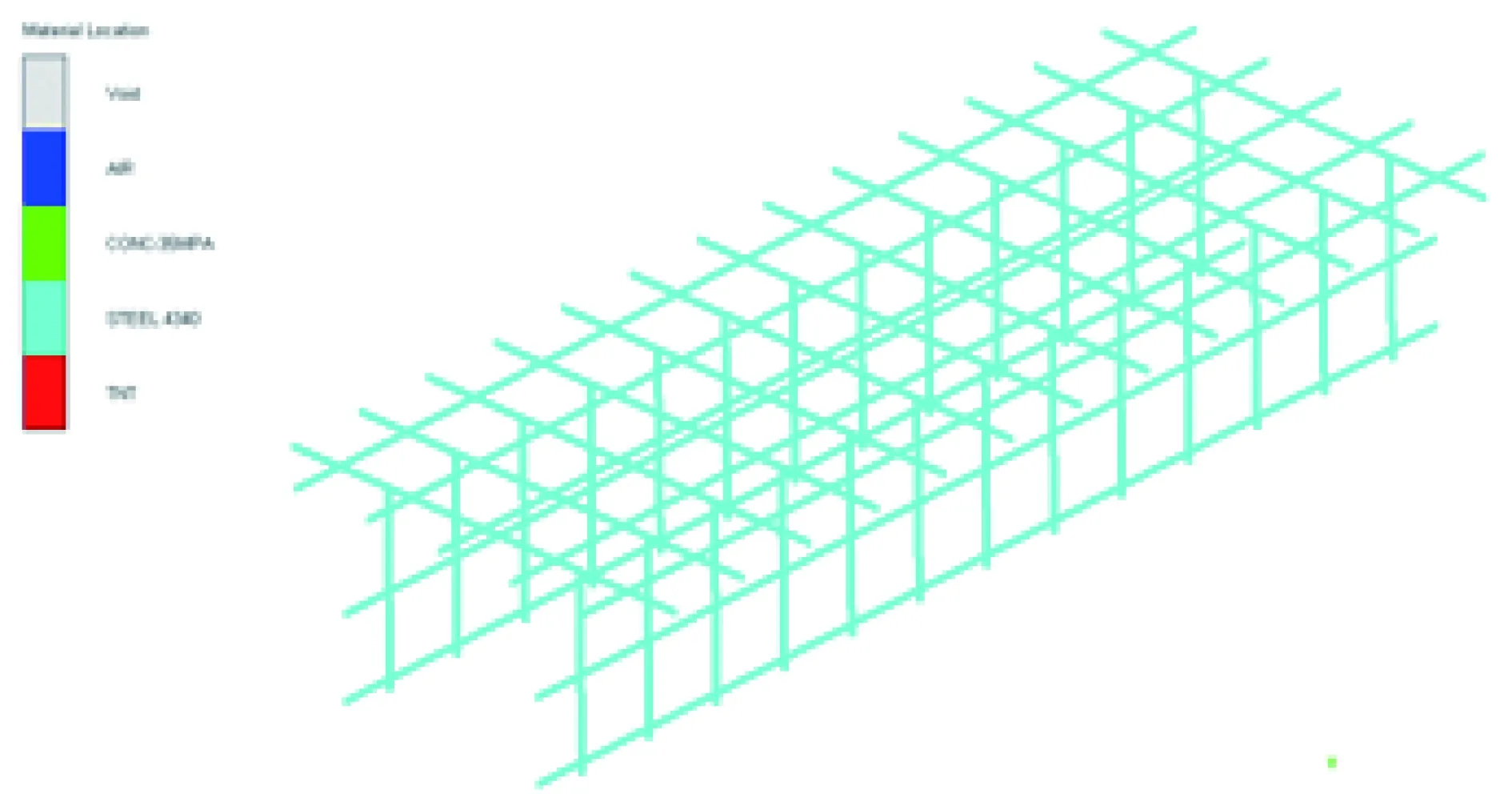
图2 钢筋的有限元模型Fig.2 Finite element model of reinforcement

图3 钢筋混凝土板的有限元模型Fig.3 Finite element model of reinforced concrete slab

图4 空气包裹下的计算模型Fig.4 The calculation model in the air

2.2 材料参数选取

对于炸药材料而言，JWL[6]状态方程是不含化学反应的经验方程，其参数由实验标定，可较好地表征爆轰产物膨胀做功过程，具体表达式为

(7)

式中：p为爆轰压力；V为相对体积；E为单位体积的内能；A0、B0、R1、R2和ω是材料常数。本章所用TNT炸药JWL状态方程参数[6]见表1所示。

表1 TNT炸药模型材料的参数Tab.1 Parameters of TNT explosive model material

炸药爆轰产物被视为理想气体，状态方程为

p=(γ-1)ρe·e

(8)

式中,爆轰产物膨胀系数γ=1.4。

混凝土采用AUTODYN软件材料库带损伤破坏的RHT[7]混凝土材料模型，该模型包括p-α状态方程，RHT强度模型和损伤模型以及侵蚀算法。混凝土的材料模型参数[3-4]如表2所示。

表2 混凝土材料参数Tab.2 Parameters of concrete material

钢筋采用JOHNSON-COOK材料模型[8]，该模型适合模拟材料在大变形、高应变率和高温情况下的力学性能。在爆炸载荷作用下，热传导的时间远大于爆轰持续的时间，且由于变形热导致的温升并不大，材料出现强化继而接近失效时，应力减小幅度比较有限，所以温度软化效应并不明显。该材料的本构模型可表示为

(9)

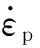
表3 钢筋材料参数Tab.3 Parameters of reinforcement material

2.3 仿真模型校核

钢筋混凝土板在20 g、60 g装药爆轰产生的冲击波和爆轰产物的作用下，在板中心产生了剪切破坏。靶板正面在爆轰产物压缩作用下，混凝土块抛掷形成漏斗坑，且背面产生混凝土的层裂破坏，形成震塌漏斗，靶板发生贯穿破坏。对比模拟结果和文献[4]中的实验结果，其破坏效果比较如图5～6所示。

(a) 模拟结果 (b) 试验结果图5 直径4 cm、质量20 g装药数值模拟结果和试验效果对比Fig.5 Comparison of numerical simulation results and experimental results of 4 cm diameter and 20 g charge

(a) 模拟结果 (b) 试验结果图6 直径4 cm、质量60 g装药数值模拟结果和试验效果对比Fig.6 Comparison of numerical simulation results and experimental results of 4 cm diameter and 60 g charge

采用数值模拟对实验中的一些工况进行模拟，实验数据与仿真结果对比如表4所示。

表4 数值模拟与实验结果对比Tab.4 Comparison of numerical simulation results and experimental results

从图5～6和表4可以看出，接触爆炸载荷作用下，钢筋混凝土板贯穿直径的数值模拟结果与实验结果吻合较好，可以认为数值仿真模型建模和材料参数设置合理可靠，可用作进一步的模拟分析。

继续开展数值模拟研究，对不同装药直径、不同长径比的药柱接触爆炸震塌结果进行预测，得到不同装药直径和长径比条件下接触爆炸震塌预测结果，如表5所示。

表5 不同装药直径和长径比条件下接触爆炸震塌预测结果Tab.5 Prediction results of contact explosion collapse under different conditions of diameter and length to diameter ratio

3 装药长径比对接触爆炸贯穿效应的影响分析

接触爆炸载荷作用下，钢筋混凝土板的破坏可以分为爆炸成坑、背面震塌和爆炸贯穿3种典型模式，如图7所示。本文接触爆炸板的主要毁伤特征如图7(b)、(c)所示，为正面成坑与背面震塌和爆炸贯穿。

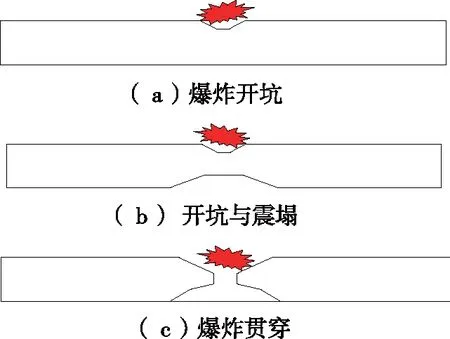
图7 接触爆炸局部破坏模式Fig.7 Partial damage mode of contact explosion

通过对表5中的数据进行无量纲化的处理拟合发现，当装药长径比一定时，无量纲贯穿直径与无量纲装药直径之间的关系如图8所示。从图中可以看出，当无量纲装药直径d/D趋近于零时，装药直径D趋近于无穷大，无量纲贯穿直径R0/D是增大的；当无量纲装药直径趋近于无穷大时，装药直径D趋于零，无量纲贯穿直径R0/D也趋于零。因此，无量纲贯穿直径和无量纲装药直径之间可能存在幂函数形式。假设存在幂函数关系可将式(6)转化为

(10)

从图8的数据可以看出，当装药长径比不变时，式(10)中等式右端的f函数为一定值。由图8中拟合的曲线可以得到，式(10)中的指数值为-0.30。因此，式(10)可进一步转化为

(11)

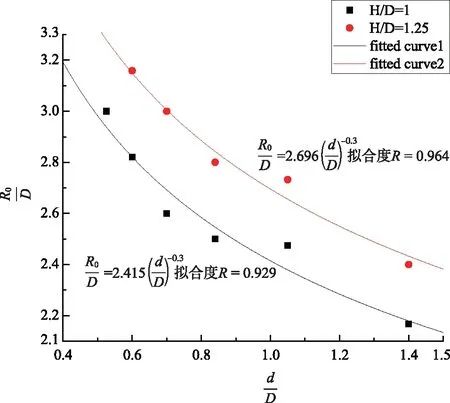
图8 无量纲贯穿直径与装药直径的变化趋势Fig.8 Trends in dimensionless penetration diameter and charge diameter

图9 无量纲贯穿直径与装药长径比之间的关系曲线Fig.9 Trends in dimensionless penetration diameter and the length to diameter ratio

从图9中可以看出，函数曲线中无量纲贯穿直径随药柱长径比的增大呈递增趋势，并且增长速率逐渐变小，存在极值。

通过对文献[4]中的实验数据和本文数值模拟的结果进行拟合得到贯穿直径跟装药长径比、装药直径之间的关系式为

(12)

从图9可以看出，式(12)的曲线形式与实验数据和数值模拟结果的增长趋势吻合较好，无量纲的贯穿直径随装药长径比的增大而增大，且存在极限的无量纲贯穿直径。

4 装药长径比对接触爆炸正面破坏和背面震塌的影响分析

利用与贯穿直径同样的分析方法，对板的正面破坏直径的数据进行拟合，得到图10～11所示的关系曲线，并得到计算正面破坏直径的公式为

(13)

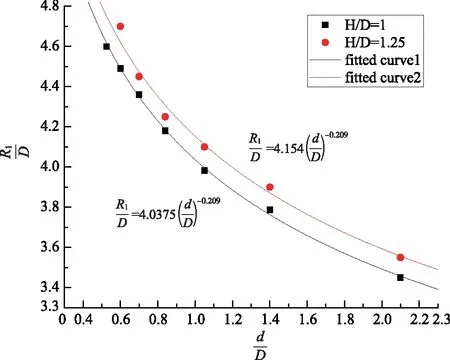
图10 无量纲正面破坏直径与装药直径的变化趋势Fig.10 Trends in dimensionless damage diameter and charge diameter

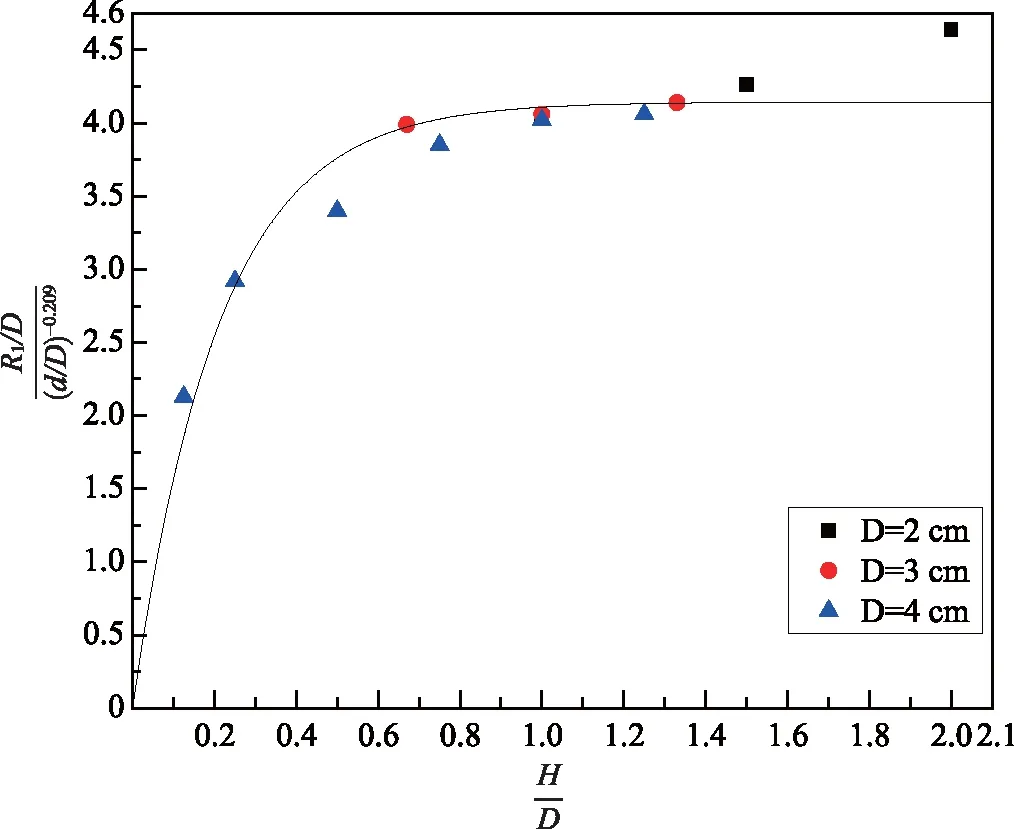
图11 无量纲正面破坏直径与装药长径比的关系曲线Fig.11 Trends in dimensionless damage diameter and the length to diameter ratio of charge

从图11可以看出，式(13)的曲线形式与实验数据的增长趋势吻合较好，无量纲的正面破坏直径随装药长径比的增大而增大，且存在极限的无量纲正面破坏直径。通过量纲分析得到了接触爆炸载荷作用下，钢筋混凝土板正面破坏区的工程计算公式。

利用同样的方法，对钢筋混凝土板的背面震塌区直径的数据进行拟合得

(14)

5 结束语

通过量纲分析明确了柱形装药接触爆炸条件下影响钢筋混凝土板破坏特性的主要影响因素为装药的长径比、装药直径、钢筋混凝土板厚。

利用AUTODYN有限元软件建立的流固耦合数值模拟方法，可以很好地模拟接触爆炸加载中钢筋混凝土板正面混凝土破碎失效、靶板贯穿、混凝土背面震塌等破坏效果，且和实验结果吻合较好；数值模拟结果表明，装药与板接触爆炸震塌破坏是存在极限装药长径比和极限贯穿直径的。

在有限元数值模拟和量纲分析的基础上，提出了预测接触爆炸条件下，钢筋混凝土板破坏效应(包括正面破坏区、贯穿区和背面震塌区)的工程计算公式，对反建筑物战斗部的研究设计及战斗部作用下建筑物目标的毁伤评估具有一定的参考价值。