考虑多场耦合效应的飞行器头罩热防护结构数值分析

李宗阳，李 煜，程广益，窦怡彬，张晓宏

(上海机电工程研究所，上海 201109)

0 引 言

临近空间飞行器关键技术包括飞行器总体设计技术、多学科优化设计技术、超燃冲压发动机技术以及长时间高温热防护技术[1-2]。其中，长时间高温热防护技术涉及到热防护材料的研发、热防护结构的设计以及热防护结构的试验验证等方面。临近空间飞行器热环境的确定是进行热防护设计的前提和依据，数值仿真和地面试验是获取临近空间飞行器热环境以及进行热防护设计和验证的主要手段。由于多场耦合效应的多场耦合分析技术可以更为准确地分析飞行器的热环境，因此，国内外学者在多场耦合领域做了大量的工作。1987年，美国学者ALLAN等针对飞行器前缘气动热环境以及激波干扰分布情况等问题，开展了圆柱气动加热试验，详细研究激波相互干扰的流场分布以及结构传热情况[3-4]。2010年，赵晓利等考虑流动传热和结构传热之间的相互影响，对圆管气动加热试验进行了三维数值模拟，得到的结果与试验值符合，实现了流动传热耦合的准确计算[5]。2011年，CULLER等根据多场耦合分析中各物理场的特征时间，采用准静态多场耦合分析方法对C/C复合材料进行多场耦合分析，并比较了单/双向耦合分析、时间步长以及迭代步数对结果的影响[6]。2014年，德国学者FRAUHOLZ等采用基于有限元求解器的多场耦合分析方法，模拟了二维进气道流动传热耦合问题，并针对进气道壁面为不同材料以及不同内壁温度的情况，展开对进气道性能影响的分析[7]。

飞行器头罩是整个飞行器气动热最为严酷的部位之一，因此头罩的热防护结构设计也成为飞行器热防护工作研究的重点[8]。本文在充分考虑各物理场之间的强弱耦合关系的基础上，应用将考虑流动传热全耦合的有限体积法和热结构弱耦合的有限元法相结合的多物理场耦合分析方法，对不同形式的飞行器头罩热防护结构进行数值分析，得到了飞行器头罩的热环境以及头罩热防护结构内部的温度和热应力分布，可为飞行器头罩的热防护设计提供参考。

1 数值计算方法

基于有限体积法的流动传热全耦合计算方法是将流体区域流动传热控制方程和固体区域传热控制方程写成统一的格式，采用统一的离散格式进行离散，并在同一求解器中进行求解，从而实现流体区域流动传热和固体区域的传热全耦合计算。在进行流体区域计算时，连续性方程采用可压缩流动方程，动量方程采用雷诺平均的Navier-Stokes方程，不考虑内部热源、质量力以及热辐射，流体区域流动传热控制方程的微分形式可以统一表述为

(1)

式中：W是守恒变量；Fi是无粘通量；Gi是粘性通量；Xi是坐标分量，表达式分别为

(2)

式中：ρ表示流体密度；u、v、w分别表示空间坐标3个方向上的流动速度；i、j、k分别表示空间坐标3个方向的单位矢量；E表示流体控制体的总能量；p表示流体压力；τ表示流体粘性应力张量；q表示热流密度。同样，在不考虑内部热源以及热辐射的前提下，固体区域传热控制方程的微分形式可以描述为

(3)

式中：ρs表示固体材料的密度；k是材料的热传导系数；表示拉普拉斯算子；T代表温度；h代表焓，本文计算所采用的气体模型是热完全气体模型，其焓值是随温度变化的函数，可表示为

(4)

式中：Cp为定压比热容；Tref表示参考温度。

结构温度变化会引起结构体积发生变化，同时，内部温度场分布不均匀会导致结构产生的热变形不协调，因此会产生热应力。结构的总应变由弹性应变和热应变组成，总应变张量可表示为

(5)

胡克定律阐述了物体应力和应变之间的关系，即弹性体的本构关系。假设固体材料是各向同性材料，弹性应变张量可以表示为

(6)

式中：ET为材料的弹性模量，其值是随温度变化的；σij、σkk为应力张量；υ为材料的泊松比；δij表示克罗内克符号。

假设材料热膨胀是线性的，其热应变张量为

(7)

式中，αT为材料的热膨胀系数，其值是随温度变化的。

2 多物理场耦合策略

本文所采用的多物理场耦合计算方法是涉及流体和结构的热流固耦合计算，其中流体与固体区域的流动传热耦合计算是基于有限体积法并采用统一形式的方程进行求解的，同时需要满足流体和固体交界面上的热通量和温度的守恒，可以表示为

Tfluid=Tsolid

(8)

(9)

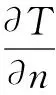
结构热变形的计算采用单向耦合的计算方法，即将流动传热耦合计算出的结构表面压力以及结构内部温度作为初始变量，展开结构热力耦合分析。本文假设结构发生的变形是小量，忽略结构变形对流场的影响。

3 多场耦合方法验证算例

3.1 风洞试验概述

圆管前缘气动加热试验是多场耦合领域的一个非常经典的试验。该试验是1987年ALLAN等在NASA兰利研究中心的高焓风洞中完成的，目的是研究二元进气道前缘的结构传热特性。试验给出了圆管前缘壁面的压力和热通量分布数据，常作为验证多场耦合计算方法准确性的算例。试验中不锈钢圆管的外径是38.1 mm，内径是25.4 mm，文献[3]中详细列出了不锈钢圆管壁面的压力分布和冷壁热流分布。

3.2 计算模型及网格

数值模拟的来流条件在表1中给出，其中，p∞、T∞分别指自由来流的压力和温度。不锈钢的材料参数在表2中给出，其中，λ是材料的热导率。湍流模型对壁面冷壁热流的计算精确度有很大的影响。本文采用MENTER提出并改进过的剪切应力传输(shear stress transfer, SST)k-ω湍流模型[9]。该湍流模型综合了k-ε湍流模型和k-ω湍流模型的优点，可以使SSTk-ω湍流模型同时适用于分离流和附着流，并且具有较高的精确度。近壁面网格的分布对近壁面温度以及壁面冷壁热流的影响比较大，文献[10]指出可以采用当地网格雷诺数来确定近壁面第一层网格高度，其计算公式为

Relocal=ρUΔn0/μ

(10)

式中：ρ为流体的密度；U为流体相对于壁面的切向速度；μ为动力粘性系数；Δn0为第一层网格高度。为了保证计算结果的精确度，当地网格雷诺数应不大于3，因此近壁面第一层网格的高度为1×10-6m。采用ICEM软件划分网格，并用自适应网格技术对激波发生区域的网格做加密处理，网格模型如图1所示。

表1 自由来流条件Tab.1 Free stream condition

表2 材料物理属性Tab.2 Physical properties of material

图1 流场及结构域网格Fig.1 Grids of flow field and structural domain

3.3 数值模拟结果分析

在流动传热耦合计算时，设定固体区域初始温度为294.4 K，时间步长为1×10-4s。图2是采用本文的计算方法得到的流场密度云图与试验结果纹影图的对比。图2中，流体密度突变的位置就是圆管前缘脱体激波发生的位置，试验纹影中圆管前端黑色线条即脱体激波。通过对比可以发现，数值模拟的结果中脱体激波的位置以及形状都与试验结果吻合。

图2 计算得到的流场密度与试验结果对比Fig.2 Comparison of calculated flow field density and test result

圆管绕流试验的数据处理方法是采用驻点的压力p0和热流密度值q0对圆管壁面的数据进行归一化处理。驻点为坐标原点，横坐标为圆管壁面各点和圆心连线与驻点和圆心连线之间的夹角θ。图3是圆管壁面压力p分布曲线，可以看出本算例数值计算的结果与试验值是吻合的，圆管前缘驻点处压力值是35 636.6 Pa，与试验结果的误差在6%以内，这说明采用本文多场耦合计算方法计算出的气动压力数据是可信的。

图4(a)是圆管壁面冷壁热流计算结果与试验结果的对比曲线图，图4(b)是圆管壁面热壁热流计算结果与试验结果的对比曲线图,q为壁面热流值。从圆管壁面冷壁热流与试验结果的对比曲线中可以看出，二者吻合得很好，其中数值计算的驻点热流值是653 320.9 W/m2，与试验结果误差在2.55%以内。从不同时刻圆管壁面热壁热流与试验结果的对比曲线中可以发现，热壁热流变化明显的位置在驻点附近，这是因为驻点附近结构表面的温度变化较大。

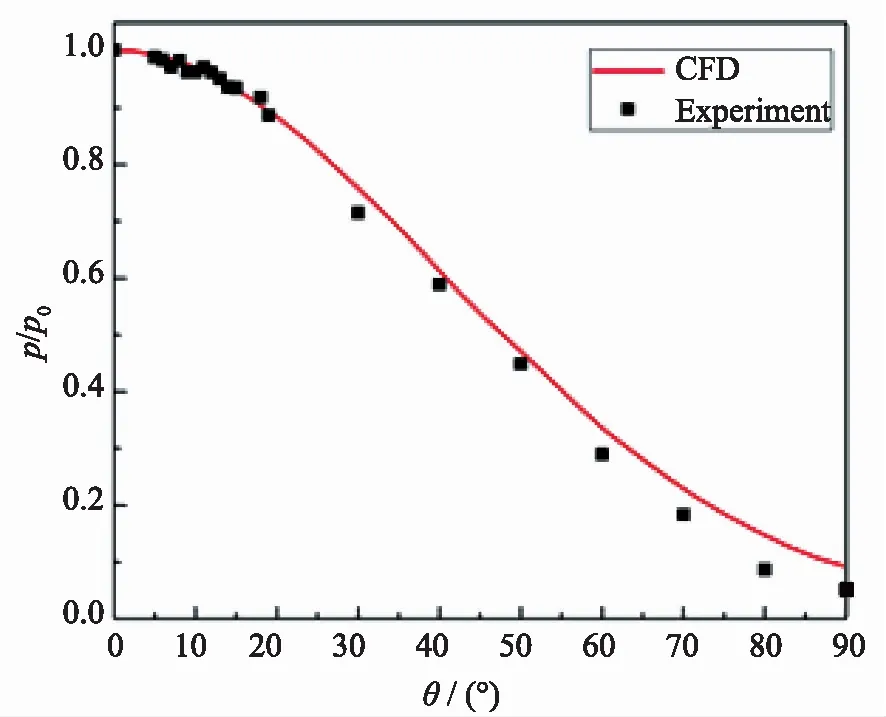
图3 圆管壁面压力分布曲线Fig.3 Curve of pressure distribution on the cylinder wall

图5表示的是不同时刻壁面温度分布曲线，其中实点代表的是5.0 s时刻试验得到的壁面温度，这与数值计算出的壁面温度非常符合，整体误差在2.35%以内。

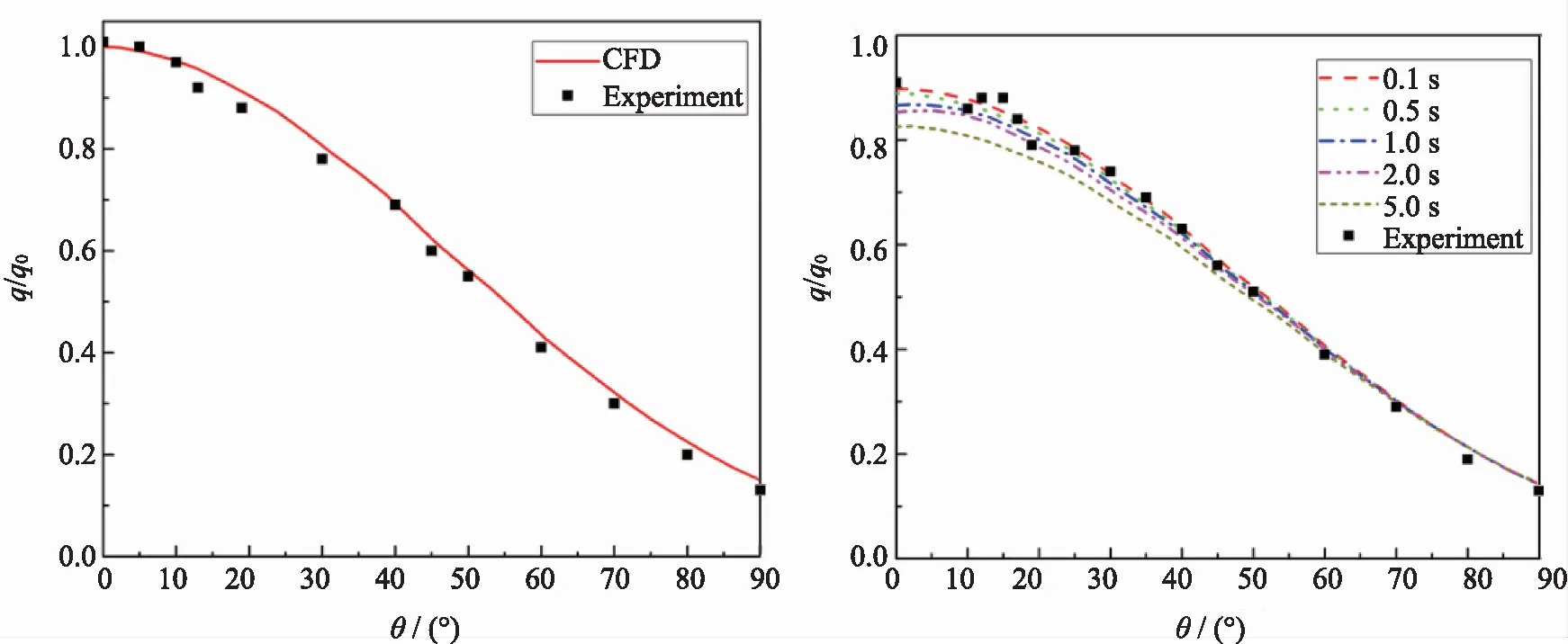
(a)冷壁热流分布 (b)热壁热流分布 图4 壁面热流分布曲线Fig.4 Distribution curve of the wall heat flux

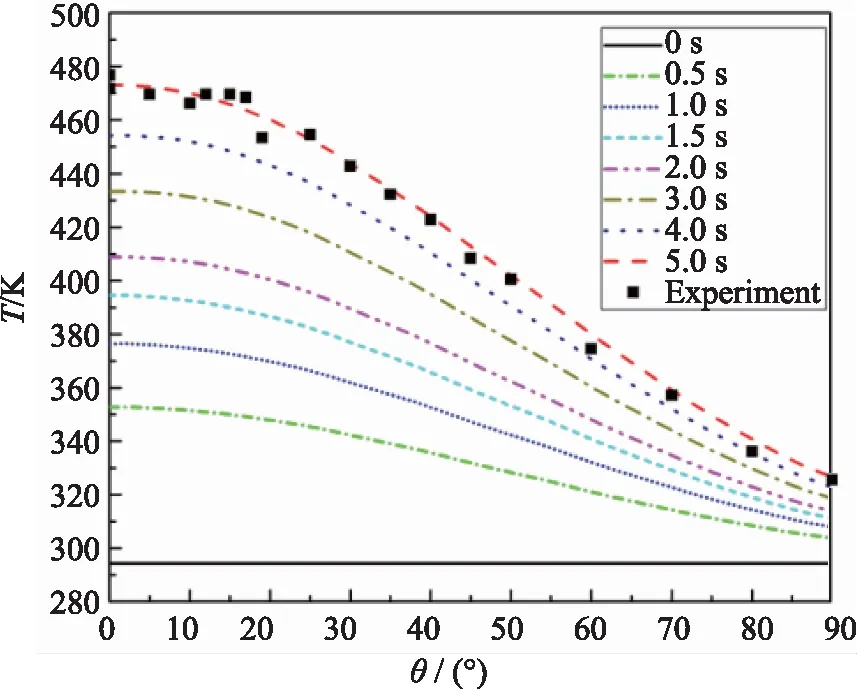
图5 不同时刻壁面温度分布曲线Fig.5 Temperature distribution curve at different time

基于von Mises应力准则，采用有限元法进行结构热力响应分析，分别给出2 s时刻和5 s时刻的圆管等效应力云图，如图6所示。图6(a)为2 s时刻的等效应力云图，图6(b)为5 s时刻的等效应力云图。可以看出，最大等效应力出现在圆管的前缘部分，并且最大等效应力随着时间推移逐渐增大，在2 s时刻最大等效应力是275.4 MPa，在5 s时刻最大等效应力是330.78 MPa，这是因为圆管结构的温度逐渐升高。

(a) 2 s时刻 (b) 5 s时刻图6 结构等效应力分布云图Fig. 6 Equivalent stress distribution of structure

4 飞行器头罩数值分析

针对飞行器头罩展开多场耦合计算分析，按金属结构和多层热防护结构两种结构类型进行分析，得到头罩结构温度场以及应力应变场，为飞行器头罩结构热防护设计提供参考。

4.1 几何模型及网格

飞行器头罩的几何外形和网格模型如图7所示，其中多层热防护结构头罩外形尺寸与金属结构一致，由外向内第一层是耐烧蚀层，第二层是隔热层，第三层是金属层。采用ICEM软件划分流体域和结构域一体化的结构网格，并在激波发生区域进行网格加密处理，第一层网格高度是2×10-6m，网格增长率是1.15，网格总数是19万，其中流体区域15万，固体区域4万。

4.2 数值计算与分析

本文对飞行器头罩进行多场耦合分析，分别对金属头罩和防热头罩进行数值分析，得到飞行器头罩的温度场、应力场以及热变形情况，并对两种结构形式头罩的数据进行对比分析。

图7 飞行器头罩网格模型Fig.7 Grid model of the aircraft hood

4.2.1 流动传热耦合分析

图8是流场特性云图，分别是流场的速度、压力和温度分布云图。在飞行器头罩前部形成脱体激波，受到脱体激波的作用，驻点前部区域气流的速度降低，压力和温度升高，驻点处的压力为4.557 MPa，驻点处的温度是1 610 K，并在此处形成一处低速高温高压区域，会产生严酷的气动加热效应。

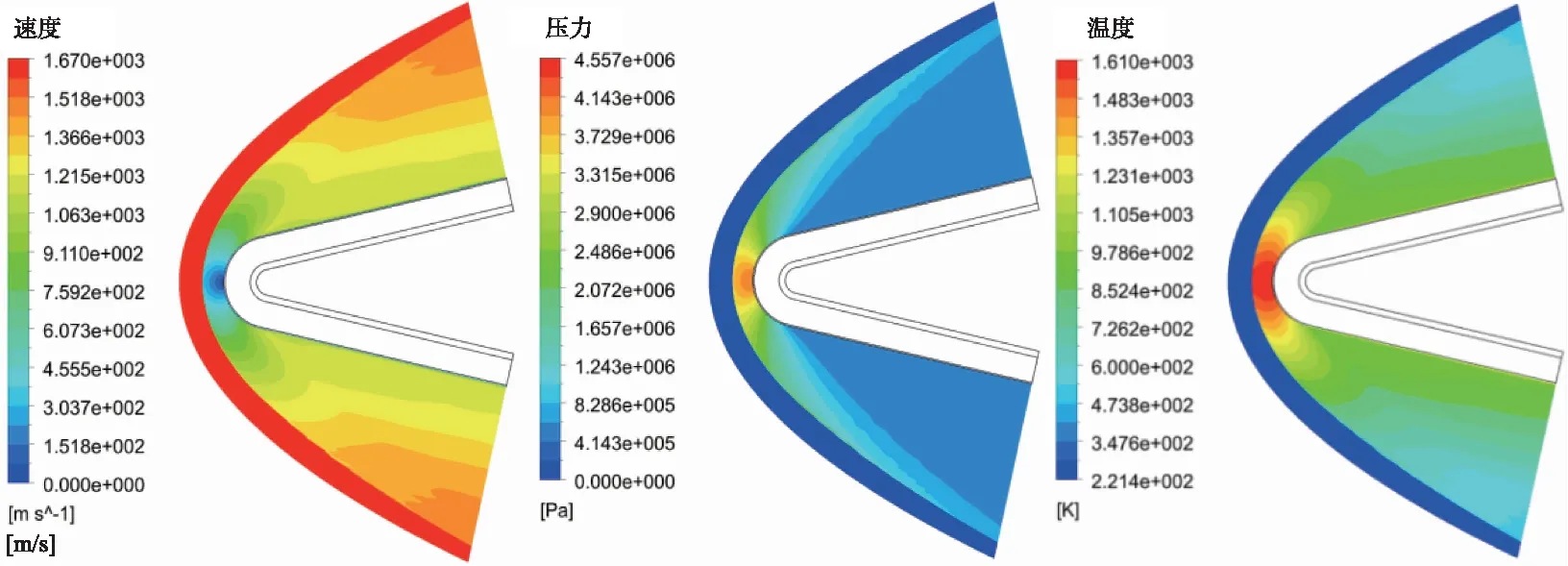
(a) 速度 (b) 压力 (c) 温度图8 流场特性云图Fig.8 Contours of flow field characteristics

图9是300 s时刻两种飞行器头罩结构温度分布云图，从图中可以看出金属结构的飞行器头罩在300 s时刻内壁驻点温度达到1 505 K，内壁面平均温度达到1 390 K，结构整体内外温度梯度较小，整体温度较高。防热结构的飞行器头罩在300 s时刻外壁面驻点温度是1 602 K,内壁面驻点温度是576 K，内壁面平均温度达到516 K，结构整体内外温度梯度较大，整体温度较低，热量主要集中在耐烧蚀层和隔热层。

(a) 金属头罩 (b) 防热头罩图9 300 s时刻飞行器头罩温度分布Fig.9 Temperature distribution of the aircraft hood at 300 s

为了研究不同结构形式的飞行器头罩结构温度随时间的变化情况，在图10中给出了两种结构形式的头罩外壁面驻点温度随时间变化曲线，可以看出防热头罩的外壁面温升比金属头罩外壁温升更快，且在300 s时刻温度基本一致。图11中给出了300 s时刻不同位置处的内壁面温度变化曲线，驻点处的X坐标是0 m，飞行器头罩根部X坐标是0.20 m，整体上看金属头罩内壁面温度比防热头罩内壁面温度高约900 K，可见防热头罩的热防护效果明显。

4.2.2 结构热流耦合分析

将流动传热耦合计算得到的气动压力载荷和温度载荷作为初始条件，采用有限元方法研究飞行器头罩结构热力响应情况。图12是两种结构形式的飞行器头罩在300 s时刻的等效应力分布云图。由图12可见，两种结构形式的应力场分布规律基本一致，金属头罩前缘内部位置最大应力为870 MPa，防热头罩前缘内部位最大应力为342 MPa，可见防热结构可以降低结构的应力。

图10 飞行器头罩外壁面驻点温度曲线Fig.10 Temperature distribution curve of the stagnation point at the outside wall

图11 飞行器头罩内壁面不同位置处温度曲线Fig.11 Temperature distribution curve of the stagnation point at the inside wall

(a) 金属头罩 (b) 防热头罩图12 飞行器头罩等效应力分布Fig.12 Equivalent stress distribution of the aircraft hood

图13是300 s时刻两种结构形式的飞行器头罩热变形分布云图，可见金属头罩发生最大变形的位置在驻点处，最大变形为4.2 mm。这是由于飞行器头罩根部约束导致结构受热后发生膨胀。防热头罩前缘区域的热变形也是指向结构外部的，外部驻点处的最大变形为0.52 mm，内部驻点处的变形为0.49 mm，远小于金属头罩的热变形。

5 结 论

本文对流动传热耦合有限体积法和热力耦合有限元法相结合的多物理场耦合计算方法进行了探索，并应用该多场耦合计算方法对圆管绕流试验进行仿真分析。结论如下：

1) 本文所提出的多场耦合计算方法可用于对圆管绕流试验进行仿真分析，得到的圆管壁面压力和热流值与试验结果相符，验证了本文方法的准确性和可靠性。

2) 经过对金属头罩和防热头罩进行多场耦合仿真分析，得到了飞行器头罩的温度场、应力场以及热变形情况。由仿真数据可知，金属头罩内壁面温度比防热头罩内壁面温度高出约900 K，金属头罩内壁驻点处的应力比防热头罩内壁驻点处的应力高出529 MPa，金属头罩最大热变形为4.2 mm，防热头罩最大热变形为0.52 mm，该结果可以为飞行器头罩的防热及结构设计提供数据支持。