立足数学思想 涵育模型素养

（福州市长乐区洞江小学，福建 福州 350200）

在小学数学教学中，数学思想方法是数学教学的核心与精髓。学生面对繁杂问题，无法灵活地调用已有的知识和生活经验解决抽象的实际问题，究其原因是教师对学生进行数学思想方法的有效渗透及培养学生应用模型思想的能力等方面的思想意识不够到位。而数学思想中三个基本思想之一——模型思想，在提高学生数学能力和思维品质方面起到举足轻重的作用。它是解决问题的核心，具有很高的应用价值。因此，在教学过程中，教师应立足于数学思想方法，创设问题与情境，引导学生经历建模过程，体验抽象的模型思维，帮助学生从不同的角度思考和解决问题，从而提升数学素养。

一、问题与情境：感知数学模型基础

熟悉的生活情境是数学模型构建的基本保障。教师可以将学生熟悉的生活素材引入课堂，通过创设问题与情境，从具体情境中抽象出数学模型，从而初步感知模型思想。［1］例如，《求比一个数多（少）几？》的减法模型构建，可以先出示以下几个问题：

（1）小东有35 枚邮票，小西有20 枚邮票，小东比小西多多少枚邮票？

（2）小勇捡了23 个贝壳，小英捡了31 个贝壳，小勇比小英少捡了几个贝壳？

（3）哥哥和弟弟的体重分别是54 千克和38 千克，他们相差多少千克？

师：为什么这3 道题都用减法计算呢？

生：他们都是求“多多少”或“少多少”，所以用减法。

教师顺势引出大数、小数和相差数的概念，并出示“大数－小数=相差数”这一数量关系，然后引导学生自主构建“求比一个数多（少）几？”的减法数学模型。通过摆一摆、画一画、圈一圈等直观操作，引导学生初步感知数学基本模型，为今后继续学习探究加减法的变式模型、乘除法模型、路程模型、植树模型、工程模型等数学模型的构建奠定基础。［2］

二、经历与体验：抽象数学模型思维

将生活中的实际问题抽象成数学模型后再加以解释与运用，是有效地建构数学模型的本质。在教学中，教师要避免学生养成在解决问题时只会套用模型的习惯。只有真正内化的数学模型，才能促进学生思维的提升。因此，教师要结合具体情境，通过描述性语言、图形语言及符号语言相结合的方式，解释自己对所构建的数学模型的理解。［2］例如，四年级下册构建“乘法分配律”的数学模型，教师出示：“小西家的客厅长10m，宽5m，餐厅的长5m，宽3m。若以边长为1m铺地砖，一共要铺多少块？”学生通过观察发现：可以先分别求出客厅和餐厅各需要的块数，再相加，得出算式：10×5+3×5=65（块）。也可以将两个房间合并成一个房间（变成一个大长方形），先算沿大长方形的长铺，要10+3=13（块），再算一共要铺5 行（沿大长方形的宽铺）所需要的块数，得出算式：（10+3）×5=65（块）。学生经历了两次数量关系的分析过程，观察发现客厅铺了10 个5 块，加上餐厅铺了3 个5 块，实际上铺了13个5 块。因此，可以建立等式：10×5+3×5=（10+3）×5。学生结合具体的生活情境，在多变的问题中抓住不变的知识本质，初步感知并构建乘法分配律的基本数学模型：a×c+b×c=(a+b)×c。

乘法分配律与其他运算律相比，结构更为复杂，意义更为隐蔽、抽象。在教学中，教师可以结合具体情境，通过描述性语言，帮助学生理解乘法分配律的现实意义；通过图形语言和符号语言相结合的方式，帮助学生抽象出乘法分配律的直观模型。［1］由乘法分配律基本模型，可以推导出乘法分配律的变式模型，如：a×b+c×b=(a+c)×b、b×a+b×c=b×(a+c)、c×a+c×b=c×(a+b)等。只有真正理解掌握了乘法分配律的本质特征，才能在较复杂的问题情境中辨析关系，把握关键，解决问题。在小学阶段，乘法分配律运算模型的应用非常广泛，例如：

某服装商城出售一款套装，每件上衣325 元，__，买16 套这样的套装需要多少元？列式为（325+175）×16，那么横线上的信息应该是（ ）。

A.裤子的价格比上衣贵175 元

B.每条裤子175 元

C.每双鞋子175 元

此题的设计意图在于检测学生在具体情境中，对乘法分配律模型本质特征的认识。假设选项A 是正确的，那么结果则表示裤子的总价，而选项C 则与本题无关，因此正确答案应该是B。其中，325 和175 分别表示上衣和裤子的单价，算式325+175 表示一套这样的套装的价格，算式（325+175）×16 表示16 套这样的套装的总价。在教学中，教师要善于创设基本数学模型的变式情境，激励学生主动思考，培养学生养成数学建模的思维习惯，逐渐增强数学建模思想的意识，不断积累丰富的数学建模经验，有效提升分析、比较、归纳、概括、抽象、推理等方面的数学素养。

三、形象与抽象：构建数学模型方法

课堂教学借助数形结合，将形象思维和抽象思维巧妙结合，化复杂为简单，化抽象为具体，分散思维难度，利用形的直观去寻找数与数之间的关联，利用数的抽象去探索图形与图形之间的关联，实现形象与抽象的统一，从而构建数学模型，提升数学素养。例如，教师出示：“6 个点一共可以连多少条线段？8 个点呢？”随着问题的抛出，学生一开始无法构建相应的图形及其数量关系。教师可以引导学生运用化繁为简的思想方法寻找解题思路：可以从一个点、两个点、三个点等开始，尝试着边画边寻找规律。（见图1）

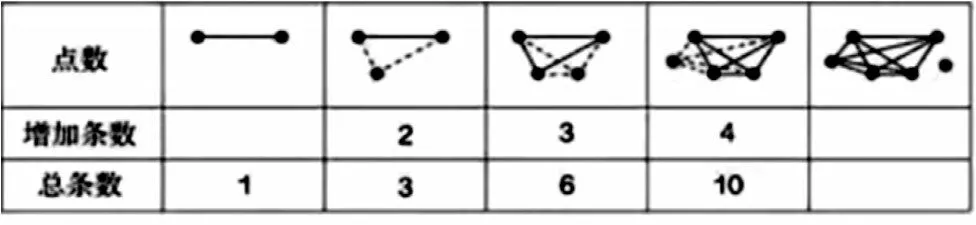
图1

学生通过画图、质疑、分析列表中的数据特点,发现：两个点可以连1 条线段，从第3 个点开始，增加第3个点时就增加2 条线段，增加第4 个点时就增加3 条线段……同理可得，6 个点就增加5 条线段，8 个点就增加7 条线段。

师追问：刚才我们通过画图发现了其中的规律，那么10 个点，20 个点，n 个点能连多少条线段呢？还需要通过画图来解决吗？

生1：从图表中发现，3 个点中任何一个点和另外两个点都能连2 条线段，那么3 个点就可能连6 条线段，因为每条线段都重复连了一次，因此6 要除以2，得出能够连3 条线段；以此类推，10 个点就可以和另外9 个点连成90 条线段，由于都重复连了一次，所以90 除以2 等于45 条；20 个点和另外19 个点连成380条，因为都重复连了一次，所以380 除以2 等于190 条。n 个点就可以连成n 乘n 减1 的差的积再除以2。

生2：每增加一个点，这个点就可以与原有的点连成线段，新增线段的条数与原来点的个数相等。通过分析推理得出n 个点所连成线段的条数：1+2+3+4+……+（n-1)。通过化简得出：n（n-1)÷2。

教学案例中，学生在画图寻找规律过程中，体验到直观图形便于观察其中的数量及数量关系。通过列表中的数据,抽象出其中的规律，从而得出“同一平面内若干个点能连成多少条线段”的答案。同样的问题，从不同的角度思考，有不同的解题方法，从而实现深度思考。学生经历了由形象到抽象的自我建模过程，在观察、比较、分析、抽象、概括、推理等方面的数学素养得到提升。

在小学数学教材中，数学模型无处不在，每一个实际问题都能够找到跟其相对应的数学模型。教师要善于创设情境，注重数学思想方法的渗透，以问题引领促思考，借助直观促想象，化形象为抽象，使学生感悟数学模型思想是解决问题的关键，增强建模意识，总结建模经验，实现有效的数学模型构建，促进数学素养的提升。