中考路径长问题之直线型路径

□福建省安溪铭选中学 刘菲芬

一、目标点到定点的连线与定直线所夹角为定值（定夹角得直线）

【题型剖析】目标点在运动过程中始终到某个定点的连线与某条定直线的夹角保持不变，而这个定点经常就是目标点的起点，这时目标点的运动轨迹就是该目标点与起点所在的直线，即为直线型路径。此时只要找到目标点的起点和终点，路径长为以这两点为端点的线段长。

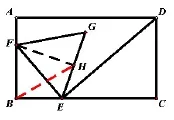
【范例点睛】例1：在矩形ABCD中，AB=3，AD=3，点E从点B出发，沿BC边运动到点C，连接DE，过点E作DE的垂线交AB于点F。在点E的运动过程中，以EF为边，在EF上方作等边△EFG，求边EG的中点H所经过的路径长。

【典例解析】通过B，E，F，H四点共圆可得∠HBE=30°，即目标点H到定点B所在定直线BC的夹角为定值，而矩形ABCD中AB=3，AD=3得∠DBC=30°，因而点H的运动轨迹为BD所在的直线。

【方法总结】①夹角法：1。找定点(一般为目标点的起点或中点或某个临界位置)；2。找目标点的过程点(可锁定题目所给图形的位置点)，然后连接过程点和定点，证明此连线与某条定直线夹角为定值；第三步：找目标点的起点和终点，求这两点间的线段长度即可。另附②解析法：题目中出现了正方形、矩形、直角三角形、等边三角形等为建立直角坐标系奠定了天然条件时可用解析法来证明目标点作直线运动，并用两点间的距离公式求路径长。第一步：以直角顶点B为坐标原点建直角坐标系；第二步：设动点坐标(x，y)，求解析式为一次函数，从而得到点H的运动轨迹为直线。第三步：求起点、终点坐标，用两点间距离公式求路径长。

二、目标点的运动轨迹为三角形（或梯形）中位线

（一）定距离得平行线

【题型剖析】此类题型中，过程点均为线段的中点，过程点在运动过程中到定线段的距离始终保持不变，根据平行线间的距离处处相等，可得过程点的运动轨迹与定线段平行，再加上中点即可证运动路径长为三角形（或梯形）的中位线。另：此类题也可通过四点共圆的几何证法，得角相等，再根据同位角（内错角）相等，两直线平行得中位线。

【范例点睛】例2：已知：如 图 ，△ ABC∽ △ ADE，∠BAC＝ ∠DAE＝90°AB＝6，AC＝8，点D在线段BC上运动。当点D从点B运动到点C时，设P为线段DE的中点，求在点D的运动过程中，点P经过的路径长。

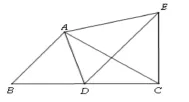
【方法总结】第一步：求出过程点到定线段的距离（或以过程点为顶点的角与某定角）相等，根据平行线的判定得出过程点的运动轨迹与定直线平行。第二步：找出过程点的起点和终点，根据中位线的定义，判断其运动路径为三角形（或梯形）的中位线。第三步：利用中位线的性质求出路径长。

（二）到两定点距离为定值得垂直平分线

【题型剖析】此类题的目标点常为某定线段的中点，而目标点在运动过程中始终与另一定线段的两个端点距离相等，即目标点的运动轨迹在该线段的垂直平分线上，从而可知该目标点的运动路径为直线型路径，并且起点和终点都为定线段的中点，得目标点的运动路径为这两线段所构成的三角形(或梯形)的中位线。

【范例点睛】例3：在矩形ABCD中，点P在AD上，AB=2，AP=1。将直角尺的顶点放在P处，直角尺的两边分别交AB，BC于点E，F，连接EF。探究：将直尺从图中的位置开始，绕点P顺时针旋转，当点E和点A重合时停止。在这个过程中，请你观察、猜想，并直接写出从开始到停止，线段EF的中点经过的路径长。

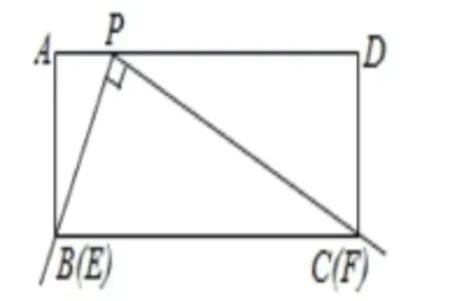
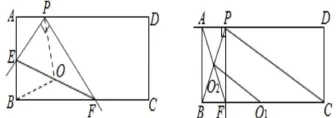
【典例解析】解：如图设线段EF的中点为O，连接OP，OB，∵在Rt△EPF中OP=EF，在Rt△EBF中OB=

【方法总结】第一步：证目标点到某定线段的两个端点距离相等（目标点常为两个直角三角形公共斜边上的中点），得出目标点的运动轨迹在该线段的垂直平分线上，从而印证直线型路径；第二步：找出目标点的起点和终点为三角形（或梯形）两边上的中点，得出目标点的运动路径为三角形（或梯形）的中位线；第三步：利用中位线定理求出路径长。