风电集团某风机产品设计及制造的学习曲线分析

季爱萍

(上海电气风电集团股份有限公司 人力资源部,上海200032)

随着全球范围内社会经济的高速增长与自然资源的不断开采利用,生态破坏与环境污染问题正威胁着人类的生存与发展,节约能源、保护环境、实现资源的可再生可持续发展已成为当前发展阶段关注的重点与热点。风能作为清洁、无污染的可再生能源之一,与传统煤、火等能源相比具有不可替代的优势,然而近些年风力发电行业的整体发展过程中仍存在一系列问题,包括政策、技术等层面的问题,核心之一仍是整体成本问题。因此,为加速我国风力发电行业的发展,应根据当前行业实际发展现状,借鉴、遵循相关经验,在风力发电发展初期,扩大风力发电的装机规模,降低风电成本[1]。本文通过运用学习曲线模型分析了风力发电设计研发、生产制造过程中降本增效的发展趋势。

1 学习曲线效应及现实意义

上海电气风电集团股份有限公司坚持以客户为中心,以“全生命周期服务”为理念,为客户提供风电全生命周期整体解决方案。经营业务涉及风电机组智能设计制造、风场智能运维、风力资源评估、数字化风场投资开发、风电场资产智能管理等。

随着产品的不断升级优化,客户对产品的设计制造、交付周期、成本控制等方面的要求不断提高,需要不断研发、试制、批量投产新型产品等高端装备制造产品。在风电新产品的设计、制造环节当中,合理把握、利用学习曲线效应,从学习曲线的角度来分析实际生产运营当中的问题,对于提高组织的生产效率有着重要的现实经济意义。

学习曲线效应又称经验曲线效应[2],或者波士顿经验曲线效应、改善曲线效应。它用来表示单位产品生产成本、生产时间与产品生产总数量之间的关系。在产品生产制造过程中,可以用学习曲线来预估判断产品的设计时间、生产时间及经济成本;在人力资源管理方面,可以用来评估基础管理的产品生产率改善状况[3]。学习曲线模型主要基于以下两个假设：

(1)每完成单位产品的设计生产或目标任务后,下次完成该单位产品的设计生产或目标任务的时间将缩短;

(2)单位产品设计生产全过程完成时间的缩短将遵循一个可预测的模式。

学习曲线的一般形式是：

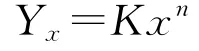
式中：x 为单位产品生产数量;Yx为制造第x个产品所需的直接生产时间;K为制造生产第一件产品所需要的直接生产时间;n 为log b/log 2,其中b代表学习率。

2 学习曲线模型在风电产品制造与交付中的应用

国际研究成果显示,风力发电、光伏发电等新能源产业的发展符合学习曲线效应[4-14]。本文以风电“铁三角”的团队作业方式为研究对象,分析学习曲线模型在风电产品设计制造过程中的应用。具体来说,以某风电机组作为研究对象,进行建模分析。风电机组的设计制造生产过程有着精益的要求,要求最高质量、最短时间、最低成本,并辅以严格的考核指标。而交付周期的长短,则直接反映出在达到产品标准的前提下制造成本的高低。假设以日为计量单位,每单件同样产品生产制造与交付时间的差异会产生8 000元/日的成本浮动。亦即,交付时间每增多一日,将会增多8 000元的价格成本;反之,交付时间每减少一日,则会降低8 000元的价格成本。而制造与安装过程所耗费的工时则直接决定了整个交付周期的长短。影响成本的另一因素是生产团队内的总作业人数,同样的人员质量,40人团队的作业效率明显优于30人团队的作业效率,与此同时也会直接增加人员成本。风电机组产品的生产、制造与交付既包含设计及制造环节的学习曲线效应叠加,也包含物流、安装、运维等方面的学习曲线效应累积,对以“铁三角”运作核心模式主导的人员团队作业、合作要求较高,展现出明显的学习曲线效应。因此,如何运用学习曲线效应及模型进行分析,评判制定出合理的团队人数与交付周期控制对于降低风力发电的成本而言非常重要。

以某风电机组产研发生产为例,需要批量设计投产本风电机组产品40件。从前期的工艺研发、到后期的生产制造,最初需要研发人员、技术人员、管理人员、操作人员共计40人。在投产交付了3件本产品后,重新调整该产品的规划运营,相关人员人数减少至37人即可组织实施交付工作。由指数曲线,可得出学习率为37/40=92.5%,如果希望合理化配置制造第40件该产品所需的人员,根据公式与实践情况可计算出学习曲线的改善值。可得,Y40=40×40log 0.925/log 2,其中92.5%学习率的第40个单位的改善系数为40log 0.925/log 2=0.660 4。由此可知,此值与最初的需要人数相乘可以计算出：40×0.660 4=26.416 1,约等于27人。也就是说,可以组建一个由27人组成的研发、技术、管理、操作的人员团队,组织该产品的设计研发、生产制作及运营交付。同样,可以在后续本产品的重复性生产交付过程中,继续探索寻找人力资源成本组合方式的最优解来稳定优化学习曲线。

为了探寻交付周期的最短值,可以从生产、制造、安装各环节所需工时的角度来进行分析。在一定的人员组合模式下,以单件产品的制造与安装工时为研究对象,统计数据如表1所示。

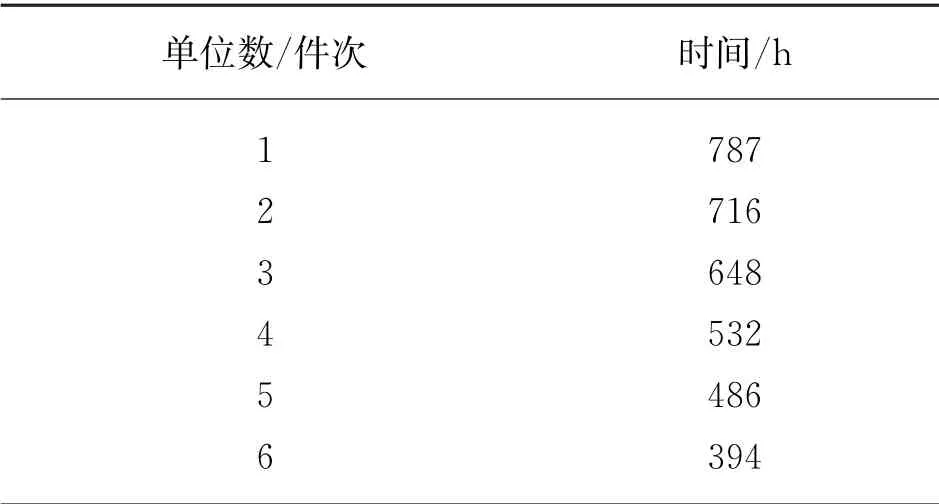
表1 前6件单位产品的制造与安装工时

通过表1,计算平均学习率可以对学习率进行预估：

第2件为716/787=91%;第3件为648/716=91%;第4件为532/648=82%;第5件为486/532=91%;第6件为394/486=81%。由此可得：平均学习率=(91+91+82+91+81)%/5=86.3%,约等于86%。

在学习率为86%的情况下,第40件制造与安装的改善系数为40log 0.86/log 2=0.448 1,可见,第40件产品的制造时间应该是：787×0.448 1=352.7 h。

在学习率为86%的情况下,查表2,可得：第40次的累计改善系数约为21.43,因此,这40件产品的总制造时间为：787×21.43=16 865.41 h,平均每件的制造工时为：16 865.41/40=421.635 3 h。

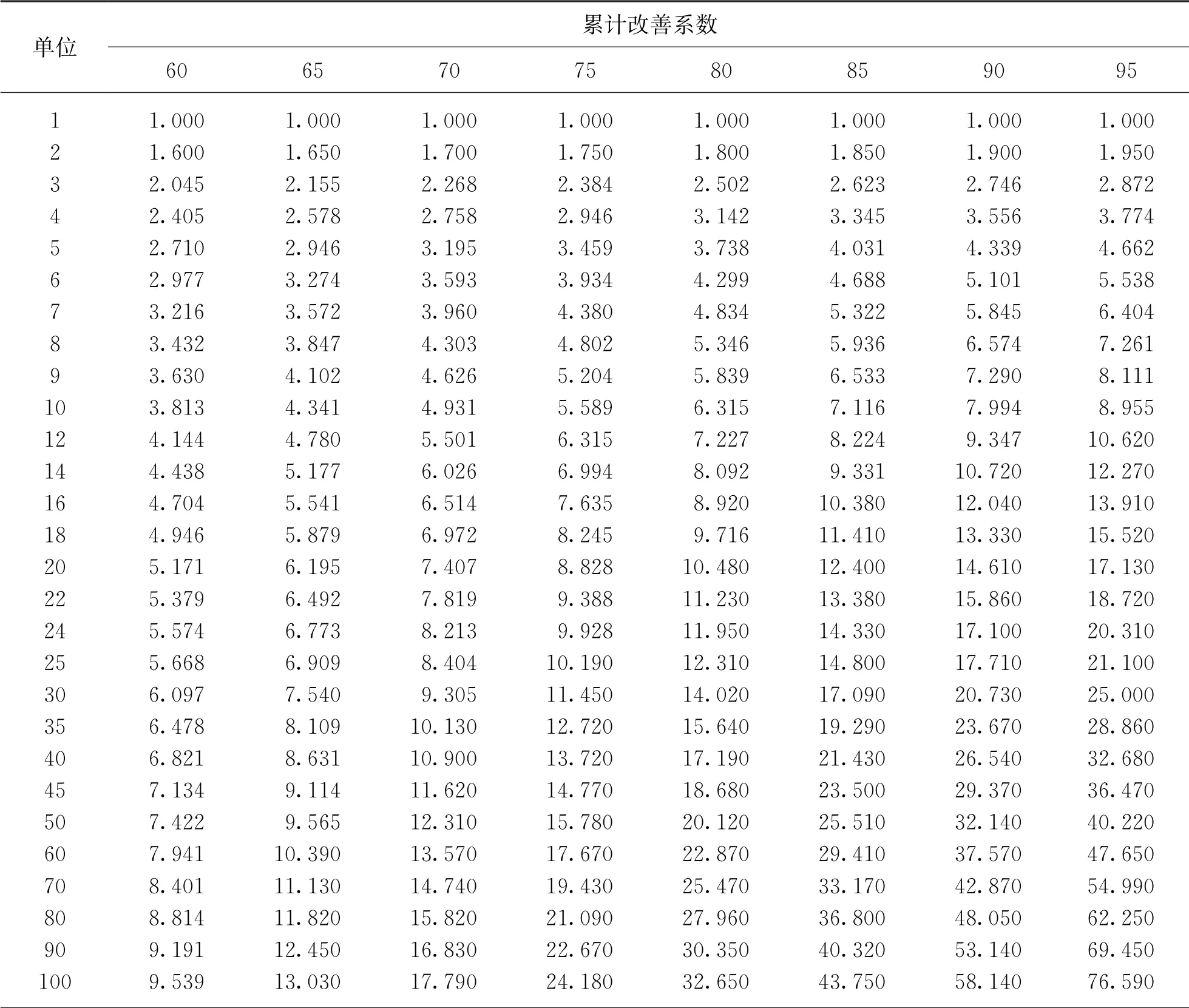
表2 学习曲线累计改善值表%

通过对该风电机组产品进行学习曲线模型分析求解可以看出,在多次重复性的生产制造同样产品后,理论上可以得出一个最优的生产绩效衡量指标与人力资源组合方式。即：在批量投产40件该风电机组产品后,形成一个至多27人的团队,可在421个工时内完成该产品的制造与安装。同时,随着学习曲线效应作用的持续发挥,可以进一步减少团队人员数量与制造安装时间,达到降低成本的目标。

3 结语

风力发电作为当前规模较大、发展较快、效果较好的新能源,在全球范围内得到较大规模的开发、普及与利用。通过运用学习曲线模型对风力发电技术成本进行研究分析,结果表明：在投产交付过程中,进一步合理配置团队人员组合与生产周期,同时,围绕某个具体产品可以开展最低成本的量化分析,比对实际投产交付过程中的指标完成情况,进行动态的差距分析与优化调整,达到降低成本的目标,实现风力发电的快速发展,提高竞争水平。