基于航路点分段的预测校正再入制导方法
章吉力,佘智勇,樊雅卓,刘 凯,安帅斌
(1.大连理工大学航空航天学院,大连116024;2.北京空天技术研究所,北京100074)
1 引 言
随着高超声速航空航天技术的进步与发展,新型的可重复使用空天飞行器为经济实用的空间往返提供了新的可行方案。空天飞行器具有速度快、可靠性高的特点,在民用和军用领域均有重大应用价值,因此在近几年一直是世界各国研究的焦点。毫无疑问,空天飞行器将大大降低空间任务的运营成本,因为它在任务之后可以进行部分甚至全部的回收,将原有的一次性成本分摊到多次发射任务中去。
基于可重复使用与水平起降的要求,空天飞行器需要具有升力面,加上其本身飞行包线宽,环境不确定性大,导致其弹道设计十分困难,尤其是在空天飞行器的再入阶段,历经真空和大气环境,速度变化大,高度下降多,可调控制变量少,精度要求高。面对高精度再入制导的挑战和要求,许多研究人员付出了巨大的努力,并提供了多种制导方法[1-7]。
数值预测校正制导算法是一种可以在线运行制导方法。该算法不需要预先存储参考轨迹,而是利用当前状态和最终目标点信息给出制导指令。由于数值预测校正制导算法使用了这种制导逻辑,即使空天飞行器在再入阶段遇到较大的扰动,偏离了预先存储的参考轨迹,制导算法也可以生成一条合适的倾侧角指令,引导空天飞行器沿着新的轨迹飞向目标点。
预测校正算法被应用在许多方面,其可行性已在多个环境的仿真中得到了验证,主要包括可重复使用的运载火箭再入,月球进入及探月飞行器再入返回,火星进入和精确着陆等。研究人员对预测校正制导算法进行了有针对性的优化。基础的预测校正制导算法由Xue S等在文献[8]中提出,并通过X-33 测试验证了算法的有效性。Wang T 等[9]提出了一种基于模糊逻辑的预测校正制导方法,利用龙格-库塔数值积分实现弹道预测。Xia Y 等[10]和Zheng Y 等[11]研究了预测校正算法在进入火星过程中的应用,验证了该算法在极低升阻比的火星着陆器上也是可行的。文献[12]给出了一种基于降阶运动方程的预测校正制导算法,降阶后的方程利用较少的计算量,就可以快速生成可行的三维进入轨迹。Wang T等[13]考虑了再入过程中的禁飞区约束,禁飞区和航路点被转换成一系列的参考点。在参考点上都设计了一次倾侧角反转。王光纶[14]首先提出使用总航程而不是剩余航程来进行倾侧角指令的迭代,这样可以避免校正算法的发散。
本文首先建立了空天飞行器在发射坐标系下的三自由度动力学模型,分析了再入阶段的过程约束和终端约束。然后,基于当前状态和目标点的终端状态,使用在线的预测-校正再入制导算法对完整的再入轨迹进行反复的数值迭代计算,得到所需的倾侧角幅值指令,达到制导精度,同时,通过对航程的在线计算,给出了倾侧角的反转逻辑。此外,为了避免再入过程后期剩余航程接近零而导致的迭代发散,文中使用再入总航程代替剩余航程进行迭代;为了避免迭代算法自身原因导致的不收敛,文中还引入一个调节因子来自适应地调整迭代步长。最后,本文通过数值仿真验证了该算法的有效性,为了解决控制指令饱和问题、增强制导律气动不确定性下的鲁棒性引入了分段方法,仿真结果表明,再入制导算法工作正常、性能良好、能够实现精度要求。
2 空天飞行器再入问题建模
2.1 发射坐标系中的动力学方程
典型的再入及返场过程如图1所示。
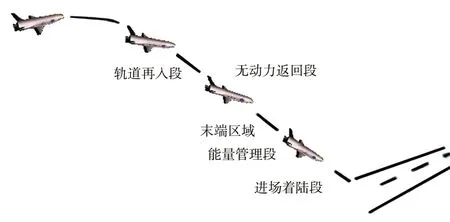
图1 典型的再入返场过程剖面Fig.1 Typical re-entry and back process
三维动力学方程在发射系中建立,位置和速度信息均被分解成了三个方向上的分量来表示,发射坐标系O-xyz定义如下:O为空天飞行器发射点,也是空天飞行器返回原着陆场的目标点。Ox在水平面内指向射向,Oy在竖直平面内指向上方,与Ox垂直,Oz由右手定则确定。式(1)~(6)给出了空天飞行器的动力学方程。

式中,x,y,z是位置坐标,Vx,Vy,Vz是速度在发射坐标系中的三个分量,X,Y,Z是气动力的分量,Fx,Fy,Fz是离心力的分量,Fgx,Fgy,Fgz是歌氏惯性力的分量,g是重力加速度,r是飞行器的地心距。
X,Y,Z的计算方法由式(7)~(9)给出。
式中,D是阻力,L是升力,θ是弹道倾角,ψ是弹道偏角。θ和ψ可以通过Vx,Vy,Vz求得,σ是倾侧角。
一般来说,再入过程的控制变量是攻角α和倾侧角σ,而攻角α的值一般由事先设定好的α-V剖面给出。预测校正制导算法能够根据给定的倾侧角预测后续航程,并基于此进行迭代得到满足航程要求的倾侧角。在本文中,倾侧角是唯一的控制变量。
2.2 再入的过程约束和终端约束
典型的再入过程约束由式(10)~(12)给出。

式中,˙是热流率,q是动压,n是过载系数;、qmax、nmax即是对应的热流率、动压、和过载的约束。kQ是与飞行器本身相关的常数,Vc=是一个无量纲化参数,L是升力,D是阻力。
对于末端需要满足的约束,终端的高度,速度以及航程需要满足式(13)。

其中高度和速度又可以用能量来进行统一表示:
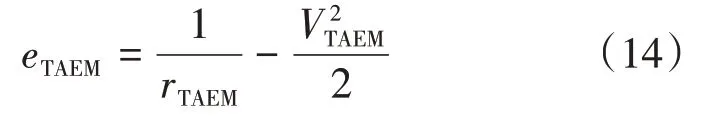
因此式(13)表示的终端状态约束还有一个等效的表达形式为:

式中,ef表示终端能量,sf是再入过程的总航程,eTAEM和sTAEM是相应的能量和航程的约束。
3 预测校正制导算法
预测-校正制导方法(也称预测制导法)是以消除实际飞行轨迹的预测落点和期望落点之间的偏差为目的的制导方法。该方法的基本思想是利用机载计算机在线预测飞行轨迹的终端点,并将求解出的终端点状态与理想状态比较得出预测终端误差,制导系统根据预测终端误差校正制导指令,使得飞行轨迹的预测终端误差为零,其工作原理如图2所示。预测-校正制导方法按照轨迹预测方式又可以分为解析法和数值法。本文重点讨论数值预测校正制导方法。

图2 预测-校正制导算法流程Fig.2 Predictor-corrector algorithm process
3.1 约束转化与再入走廊
在再入过程中,飞行器始终要遵守约束条件。但是,在全程计算和判断所有的约束是否都能满足是难以实现的,这会极大地加大运算量。事实上,由于各个约束中均含有倾侧角,可以把过程中的约束都转化为倾侧角的约束,若设置平衡滑翔段,则还需要满足平衡滑翔约束,利用准平衡滑翔条件(QEGC)可以将高度和速度约束转化为倾侧角约束。

图3 过程约束下的再入走廊Fig.3 Re-entry corridor under constraints
如图3所示,在H-V剖面上,高度的上下界由各项约束决定,高度的上界由QEGC 条件决定,高度的下界由过载、动压、热流约束的最大值决定,即:

再入过程中的约束决定了倾侧角幅值的边界,从图4中可以看出,随着倾侧角幅值的增大,再入走廊也会收窄,为了不使平衡滑翔约束与热流约束曲线相交并保留足够的裕度,需要给倾侧角设置合理的上界。

图4 不同倾侧角下QEGC边界的变化情况Fig.4 QEGC’s changing under different bank angle
事实上,根据QEGC条件:

若已知r和V,就可以求出对应的σ值。根据已经得到的Hup和Hdown,可以求得对应的地心距rup和rdown,对应的倾侧角边界由式(18)给出:

所以,控制指令σ需要满足:
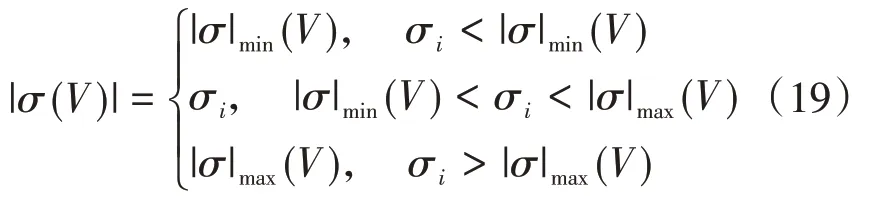
其中,σi是由预测环节的迭代算法给出的倾侧角幅值。需要注意,由于|σ|决定了飞行器在再入过程中的变向能力,|σ|min(V)的值不宜太小,通常取5°~15°。
3.2 纵向制导逻辑
如前文所述,数值预测校正制导算法的最终目的是生成倾侧角指令。而纵向制导部分的任务是确定倾侧角的幅值。
3.2.1 航程预测环节
传统的再入制导研究往往在再入点建立坐标系,使用剩余航程来迭代制导指令。然而,在再入过程接近终端时,剩余航程的值接近于0,这很可能会造成迭代发散,使算法无法获得倾侧角指令。同时,对剩余的导数进行积分来计算剩余航程的过程会带来巨大的计算量。为了解决这一问题,本文采用再入总航程来代替剩余航程。并且基于发射坐标系到地心坐标系的经纬度位置信息,提出了一种不进行积分直接计算总航程新方法。
式(1)~(6)给出了六个状态变量的导数,通过对这六个方程的积分,我们可以得到空天飞行器在每个时刻的位置和速度信息。再入航程定义在飞行过程的纵平面内。因此,通过发射坐标系到地心坐标系的转换,可以实时得到飞机的经度和纬度。通过给定一个初始的倾侧角,预测校正算法的预测环节就可以预测飞行器的最终落点,再入航程可以用式(20)计算。

式中,λ0、φ0是再入点的经纬度,λf、φf是由算法预测环节得到的目标点的经纬度,是对应的地心角。
3.2.2 指令校正环节
在航程预测环节获得了在给定倾侧角下的航程之后,指令校正环节通过牛顿迭代来求解符合要求的倾侧角指令,如式(21)所示。
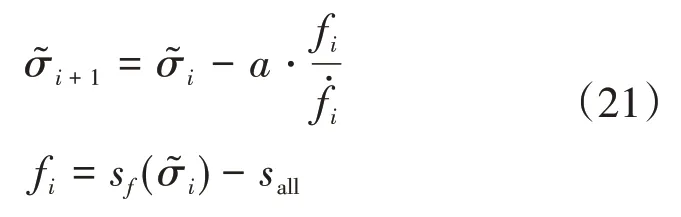
在式(21)中,a是下山因子,一般情况下,为了保证计算效率,需要给它分配一个合适的值。然而,当接近真正的解时,如果a的值太大,迭代可能陷入死循环,在真解附近振荡。迭代中的另一个问题是目标函数fi在局部的单调性可能与它的整体单调性不一致,由于局部的单调性异常,迭代可能会反向进行从而偏离正确的解,这也会产生发散。为了解决这一问题,本文给出一种自适应迭代算法,当式(22)满足时,a将缩减一定倍数。

式(21)中,sall是根据再入点和目标落点的经纬度求取的再入航程的参考值,具体求解方法由式(23)给出。
式中,λfinal、φfinal是目标落点的经纬度,Δall是sall对应的地心角。
式(20)中,目标函数fi的导数˙一般来说难以解析求取,因此在实际应用中可以采用差分来代替。
迭代算法的流程如图5所示。
3.3 侧向制导逻辑
侧向制导就是要通过合理的定义倾侧角反转逻辑来实现,在本节中反转逻辑的设计是通过定义横程和横程边界来实现。因此本文中的侧向制导律的设计就是定义横程并设计横程边界。横程边界的设计原则为使再入轨迹满足终端位置约束,又不至于使侧倾反转过于频繁。对于特定飞行器,可以通过多次仿真实验获得适当的横程边界参数。横程有多种定义方法,对于不同定义的横程,需要设计不同的横程边界。
为了定义横程,首先在横向定义横向剩余航程,由式(24)给出。
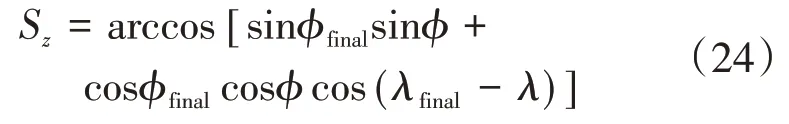
横程的定义如式(25)。
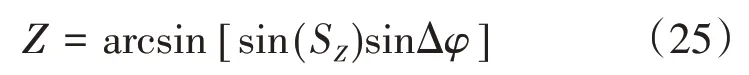
这种定义方法在倾侧角变号时,横程可以很快的响应,有较好的控制效果,航向角误差Δφ是以目标落点为基准,可以保证轨迹会逐渐趋向于目标落点。
横程的上下边界设计为:

其中,k1、k2为可调参数。因此,倾侧角符号翻转逻辑为:

因此当前使用倾侧角指令变为:

综合纵向与侧向制导,得到完整的预测校正制导逻辑如图6所示。
3.4 分段制导逻辑
全程的预测-校正制导在标称情况下一般有很好的精度,但对于长程的再入问题,气动不确定性在预测环节中的积累会影响倾侧角幅值迭代的准确性。为了进一步提升算法应对气动不确定性的性能,本文中的分段预测校正制导方法首先将再入过程分为两大段,分别是初始下降段和预测校正段,由于再入段的仿真再入点位于再入走廊之外,需要经历一个高度迅速下降的阶段才能进入再入走廊,因此在再入段前期规划初始下降段。
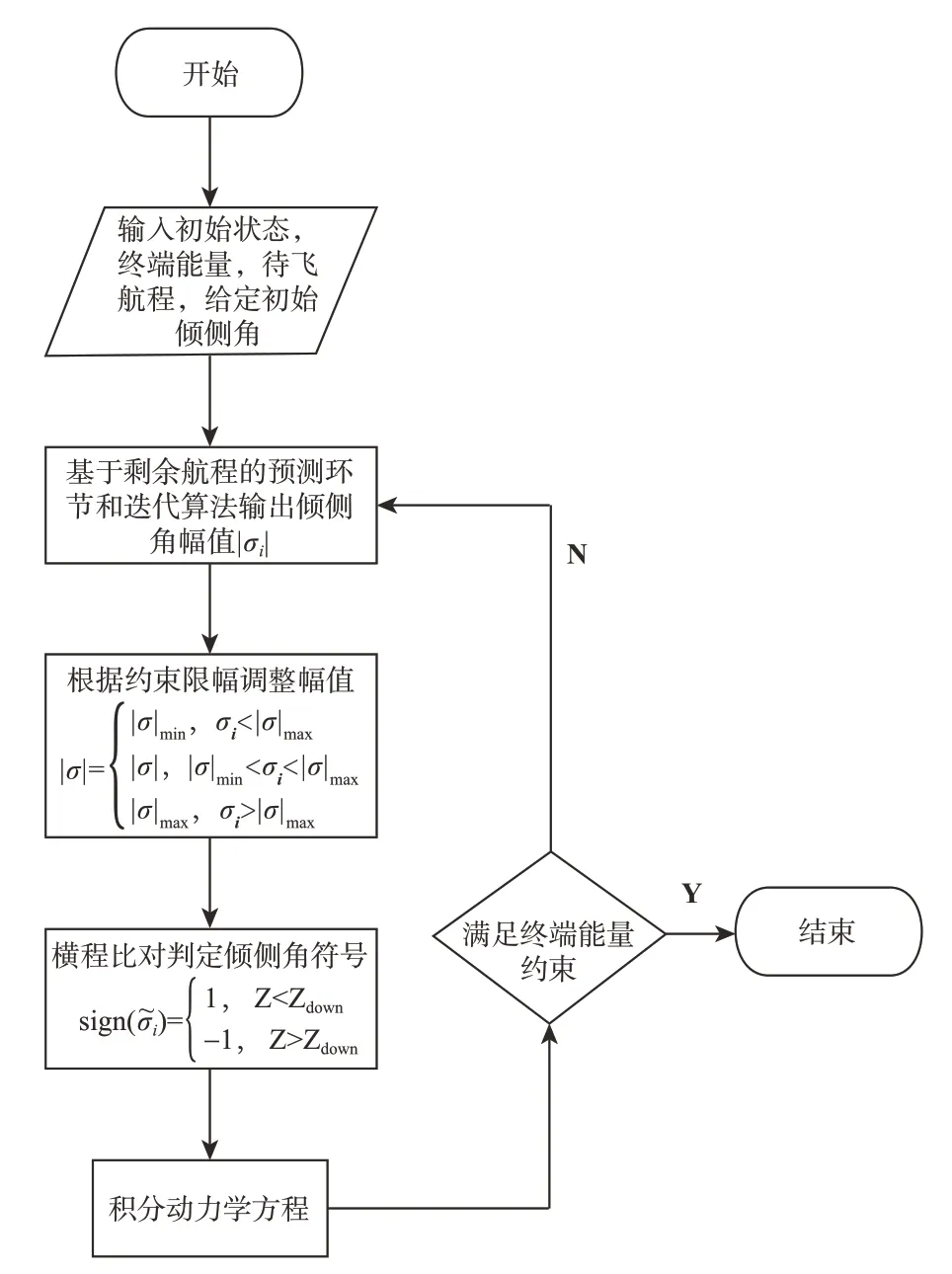
图6 预测-校正制导逻辑流程Fig.6 Predictor-corrector guidance process
初始下降段下沉率大,且由于再入飞行器尚未进入大气环境,气动力的控制能力有限。基于初始下降段的这些物理特性,在该阶段设计比较精确的倾侧角方案,或通过改变这一过程中的倾侧角来控制飞行轨迹,但效果并不明显。所以,为了避免不必要的计算量,设置初始下降段的倾侧角为一给定常值。该值由迭代算法确定,要求在使再入轨迹位于热流约束曲线之上的前提下使倾侧角尽量大,本文中设计对象以45°倾侧角飞行直至满足式(29)。

之后进入预测校正段,在进行传统的再入段轨迹规划时,往往根据物理过程把再入分为许多阶段,但这种分段方式过于复杂,不利于快速实现。预测校正制导因其只需要初始和终端状态即可进行计算的特性,使其在标称情况下运行时兼具了提供标称轨迹的功能,因此考虑在标称预测校正仿真的轨迹上选取若干航路点,以航路点为各段预测校正的终点来进行新的分段预测校正制导仿真。
4 仿真分析与制导性能评估
本文研究空天飞行器的再入阶段,初始条件由表1给出。表2给出了目标落点的相关信息。

表1 再入点初始条件Table 1 The initial conditions of the re-entry point

表2 目标落点相关信息Table 2 The conditions of the drop point
4.1 全程预测-校正制导仿真
由于每次迭代都要运行预测环节,为了减少运算时间,预测环节算法的步长比状态环节的步长要长,但是如果预测环节的状态变化很大(状态导数值偏大),算法会自动减小步长以规避误差。
如图7~8所示:制导算法能够满足速度、高度等终端约束。从图9可以看出,在飞行的前期,倾侧比较稳定。在再入过程的后期,随着横程边界的缩小和算法给出指导指令频率的增加,倾侧角开始反转。在表3中,我们可以发现落点在误差范围内。

图7 再入轨迹高度-时间Fig.7 Altitude-time of the re-entry phase
4.2 分段预测-校正制导仿真
在上节的仿真结果中,飞行末端控制指令会出现饱和,且在气动不确定性存在的情况下制导精度下降明显。

图8 再入轨迹速度-时间Fig.8 Velocity-time of the re-entry phase

图9 再入轨迹倾侧角-时间Fig.9 Bank angle-time of the re-entry phase
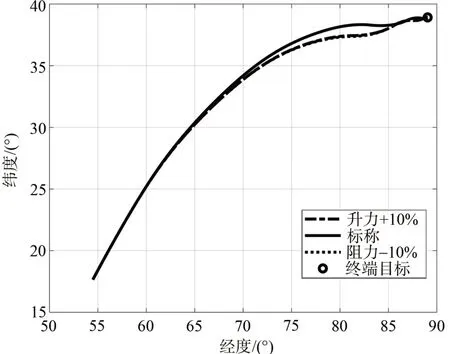
图10 再入轨迹地面轨迹-时间Fig.10 Subsatellite track-time of the re-entry phase

表3 落点误差Table 3 Error of drop point condition
本节在标称预测校正仿真的轨迹上选取若干航路点,以航路点为各段预测校正的终点来进行新的分段预测校正制导仿真,仿真弹道参数由图11~14给出。
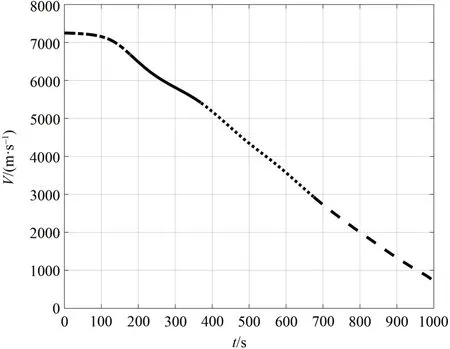
图12 再入轨迹速度-时间Fig.12 Velocity-time of the re-entry phase

图13 再入轨迹倾侧角-时间Fig.13 Bank angle-time of the re-entry phase

图14 再入轨迹攻角-时间Fig.14 Angle of attack-time of the re-entry phase
从图15中可以看到,将再入过程分段后有效的缓解了末端控制指令饱和的问题,饱和时间明显后移且不再有震荡,落点误差也被控制在3km以内。

图15 再入轨迹落点误差Fig.15 Drop point error of the re-entry phase
5 结束语
通过对仿真结果的分析,可以发现该算法在空天飞行器再入阶段工作良好。作为对数值预测校正方法的改进,本文设置航路点对再入过程进行分段,采用自适应迭代算法来提高预测校正制导算法迭代环节的收敛性和精度,有效地抑制了迭代的发散。在未来的工作中,将考虑把深度学习应用于航程预测环节,在使用本套算法获取大量仿真数据的基础上,利用AI 学习获取倾侧角与航程之间的输入输出规则,用基于数据模型的倾侧角-剩余航程映射代替原有的预测环节,由此进一步提高制导算法的计算效率。

