多飞行器的有限时间姿态一致性编队控制
刘国庆,赵 林
(青岛大学自动化学院,青岛266071)
1 引 言
近年来,飞行器编队飞行成了一个热门的研究课题,因其能够使用一些小型廉价且高性能的飞行器协同工作来代替大型的航空器去执行复杂的空间任务,例如空间信号的采集和处理、空间的检测和成像等[1]。对于多飞行器执行空间任务,其姿态跟踪能力显得尤为重要,为此很多学者提出了不同的控制方案,如最优控制策略[2],虚拟结构控制方案[3],行为控制方法[4]等。最近,一些基于图论的方法研究了多智能体系统的分布式跟踪控制[5-7],并且将该方法进一步应用于多飞行器编队飞行的研究[8]。尽管上述方案已经解决了多飞行器编队飞行的姿态控制问题,但是他们的控制系统都是渐近稳定的,收敛速率没有达到实际的期望,会影响控制系统的性能。
在飞行器的编队飞行中,快速的收敛速率对于飞行器的姿态跟踪控制来说非常重要。由于有限时间控制方案能够提供更好的收敛能力和抗干扰能力,因此很多相关的控制策略被提出。具体来说,主要有两种有限时间控制策略,一种是齐次性方法,很多学者基于此方法研究了多刚体飞行器的分布式姿态调节问题[9]和姿态包容控制问题[10],但当多飞行器系统具有惯性不确定性和未知的外部扰动时,齐次性方法就会失效[9-10];另一种是基于有限时间李雅普诺夫稳定性理论的方法,其中终端滑模控制方法和加幂积分法常用于处理各种多智能体的有限时间控制问题[11-14]。虽然终端滑模方法可以解决系统中存在的干扰,但由于引入了符号函数,控制系统会产生抖振现象[11-12]。考虑到加幂积分法会导致系统出现高增益问题[13-14],因此,有必要找到一种既能提供高精度高性能又能保证系统快速收敛并避免控制系统抖振的策略。
对飞行器系统来说,由于其动态方程是强非线性的,对其精确的控制非常困难。反步控制作为一种有效的非线性控制器设计方法,可以很好地解决这一问题并提高编队飞行的性能[15]。考虑到在反步控制设计过程中必须使用虚拟控制信号的导数,这将导致计算复杂性问题出现,因此,基于反步控制的动态面控制技术被提出[16-17],通过构造一阶滤波器巧妙地解决了计算复杂性问题。然而,在控制方案中引入一阶滤波器引起的滤波误差没有得到补偿。为了补偿由命令滤波器引起的滤波误差以获得更好的控制效果,同时避免反步设计中存在的计算爆炸问题,有限时间命令滤波反步控制方案被提出以解决各种多智能体系统的控制问题[18-19],并被进一步用于研究多飞行器编队的姿态包容控制中[20],但该控制方案忽略了多飞行器系统惯性矩阵的不确定性。考虑到飞行器在姿态变化过程中,由于附件的质量重心位移和外部环境的干扰,飞行器的惯性矩阵和控制系统将不可避免地随之受到影响,因此,具有未知惯性矩阵和外部干扰的控制系统应该被重点研究。
受以上问题的启发,本文提出了基于有限时间命令滤波反步和自适应神经网络控制技术的多刚体飞行器分布式有限时间姿态跟踪控制方案,可以很好地解决所提到的问题。
2 系统描述和准备

本文研究了具有N个跟随飞行器和1个领导飞行器的多飞行器姿态编队控制问题。对于N个跟随者和1 个领导者之间的通信用有向图论理论来描述,关于有向图论的具体描述可参考文献[18]。第i个跟随飞行器的动力学模型被描述为如下方程:其中:Ji∈R3×3,ωi=[ωi,1,ωi,2,ωi,3]T∈R3×1分别是对称惯性矩阵和飞行器的角速度;=[0,-ωi,3,ωi,2;ωi,3,0,-ωi,1;-ωi,2,ωi,1,0 ]代表ωi的反对称矩阵;ui和di分别是控制力矩和有界的外部扰动力矩阵。采用修正罗德里格斯参数pi∈R3来描述飞行器的姿态:
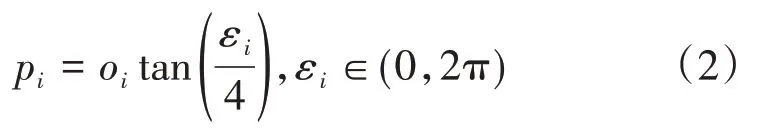
其中:εi是主旋转角,oi是欧拉坐标轴,基于修正罗德里格斯参数我们有如下运动学方程:

其中,雅可比矩阵Ti定义如下:

基于式(1)和(2),定义Q=T-1i可以得到欧拉-拉格朗日型函数:

其中,


进一步定义qi,1=pi,qi,2=,式(5)可以写成:

假设1.Ji和di都是未知的,r为领导者的姿态输出,r和其一阶导数是已知平滑且有界的信号。
性质1.未知干扰满足是一个正常数。
性质2.对于正定有界的对称惯性矩阵Joi满足不等式其中λmin,λmax都是正常数。
性质3.对于J˙io满足反对称性质qTi(Jio-2Coi)qi=0。
引理1[18].假设存在一个连续的正定函数V(t),满足+l1V+l2Vμ≤0,其中l1,l2都是正常数,μ∈(0,1),V(t)能够在有限时间T≤t0+(1/(l1(1-μ))内收敛到平衡点。
3 有限时间控制器设计
在设计控制策略的过程中,考虑设计如下有限时间命令滤波器:
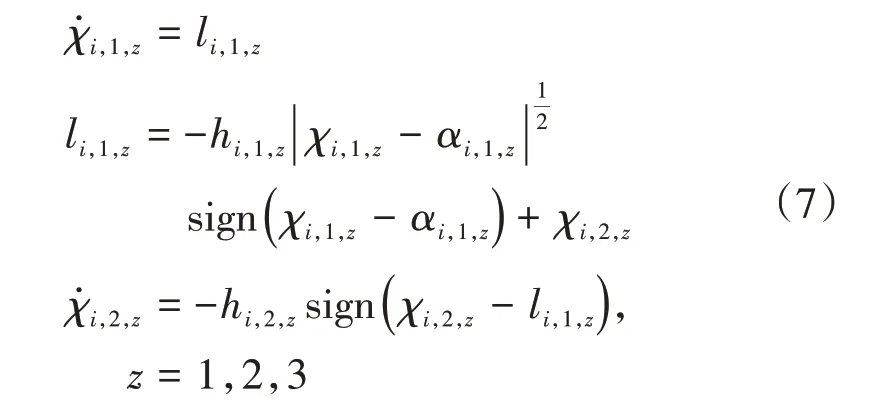
其中,hi,1,z>0,hi,2,z>0,二者都是命令滤波器的增益。
现在我们构造多飞行器的一致性姿态跟踪误差,即第i个跟随者的误差定义为:

其中,πi,2=χi,1,且χi,1是命令滤波器的输出。基于有限时间命令滤波反步技术设计如下虚拟控制信号和控制器:

其 中,ki,z,,ςi,z,z=1,2,s=1,…,n都是正常数,γ∈(0,1),γ=且γ1,γ2都是奇数。
为了消除滤波误差,建立如下误差补偿信号:


其中,ιi,δi都是正常数。
此外,补偿跟踪误差信号定义为:

定理1.对于多飞行器姿态跟踪控制系统(1)~(2)在假设1 的情况下,使用有限时间命令滤波器(7),选择控制信号αi,1,ui=T-1i,误差补偿信号(10)和自适应控制律(11),则可以保证一致性跟踪误差在有限时间收敛到原点的足够小的邻域内且闭环系统中的所有信号都是有界的。
证.首先,选择如下李雅普诺夫函数:
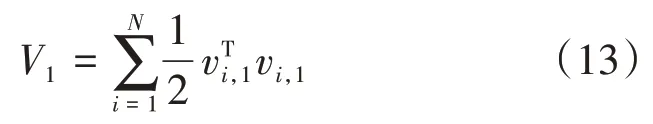
求导可得:
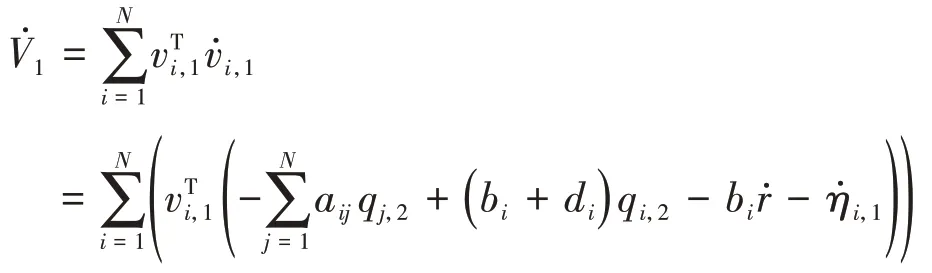

把式(9)~(10)带入式(14)可得:

选择第二个李雅普诺夫函数为:

求导可得:
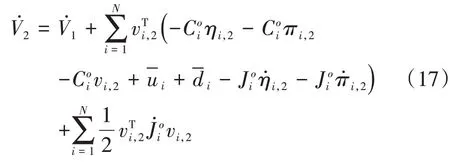

对于未知非线性动态Λi=[Λi,1,…Λi,n]T,基于神经网络逼近技术[18],可以表示为:
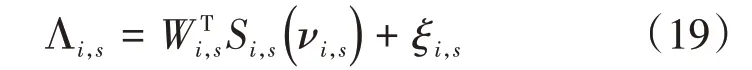
其中Wi,s=[wi,s,1,wi,s,2,…wi,s,l]T是权重向量;νi,s=然后基于杨不等式可得:

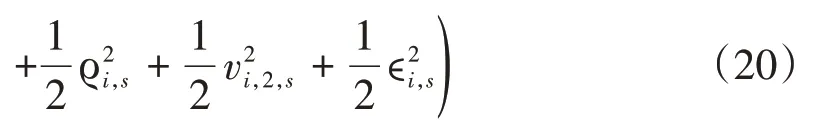
其中ϱi,s是正数。进一步考虑如下不等式:
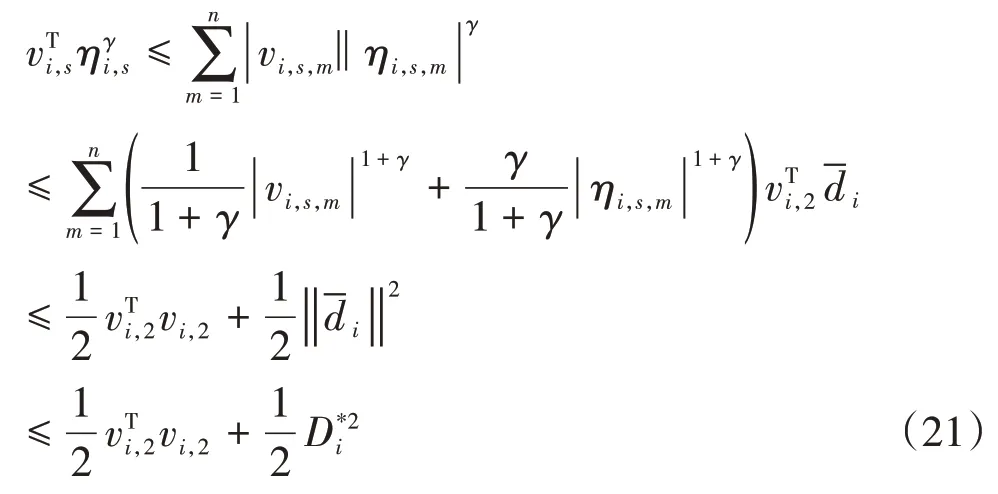
把式(20)~(21)带入式(18)可得:

进一步构造关于误差补偿的李雅普诺夫函数


其中k0=min{ki,1-1/2,ki,2},

因为=vi+ηi,选择如下李雅普诺夫函数:

求导可得:
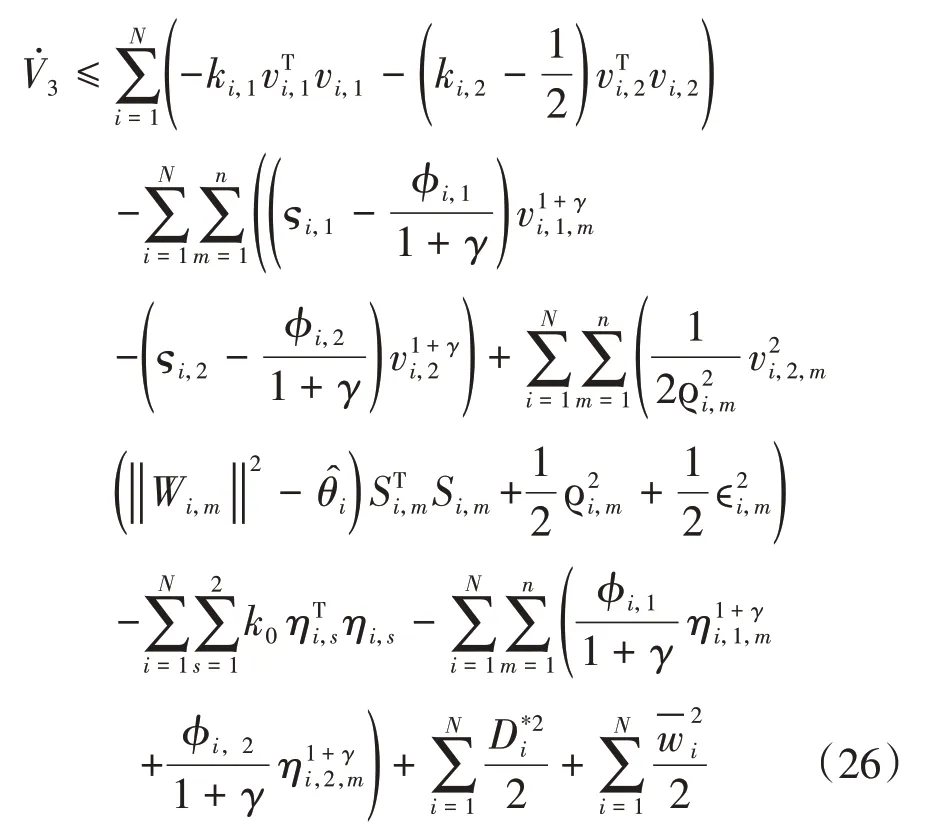
定义=θi-,进一步构造如下李雅普诺夫函数:

求导可得:

基于性质(2)和不等式:
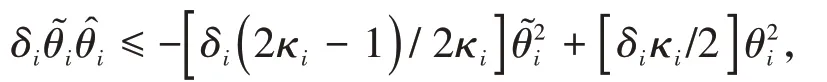
其中,κi>,可以得到:



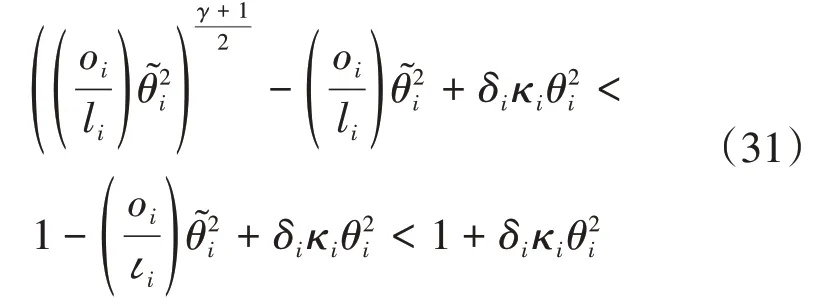
所以式(29)可以写为:

其中:Φ1=min{2ki,1,(2(ki,2-1/2))/λmax,2k0,2oi},Φ2=min{[ςi,1-φi,1/ (1+γ)]2(1+γ)/2,[ςi,2-φi,2/(1+γ)](2λmax)2/(1+γ),(φi,s/(1+γ))2(1+γ)/2,(2oi)(1+γ)/2},
进一步有:

或者:

根据式(33)或式(34)我们可以得到在有限时间内vi,s,ηi,s,会收敛到如下范围内:

姿态跟踪误差将在有限时间收敛到:

4 仿真结果及分析
在这一部分中,通过具体的例子来说明给定控制方案的有效性,一个领导飞行器和三个跟随飞行器之间的通信拓扑结构如图1所示。多飞行器系统的惯性矩阵选择为Ji=+ΔJ,其中ΔJ=diag{0.1sin(t),0,0;0,0.2cos(t),0;0,0,0.1 sin(0.5t)},分别为:

初始值分别为ω1=ω2=ω3=[0,0,0]T,p1(0)=[-0.8,1.5,1]T,p2(0)=[0.6,1,1.3]T,p3(0)=[0.7,0.8,1.1]T。领导者的输出信号选择为r(t)=[sin(t)+0.5,cos(t)+0.5,sin(t)+1]T,额外干扰设为di=0.2[sin(t),cos(t),sin(t)]T,控制器参数选择 为ki,1=ki,2=5,γ=3/5,ζi,1=si,2=25,φi,1=φi,2=2,hi,1,z=hi,2,z=220,δi=1,ιi=1。

图1 飞行器之间的通信拓扑Fig.1 The communication topology among spacecrafts
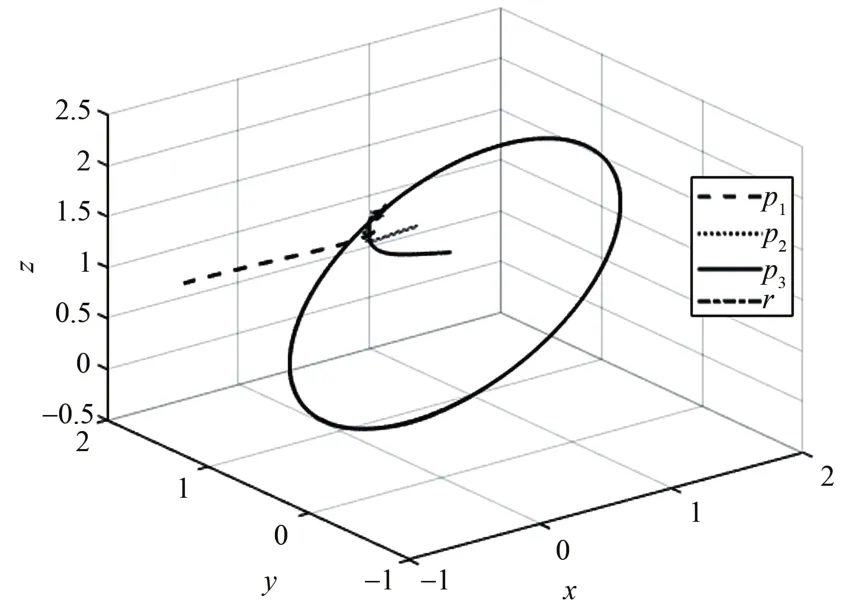
图2 pi和r,i=1,2,3的三维响应曲线Fig.2 The response curves of pi and r,i=1,2,3 in 3-D

图3 ,i,m=1,2,3的响应曲线Fig.3 The response curves of ,i,m=1,2,3
图2用3D 图展示了三个跟随飞行器的姿态在有限时间内全部跟踪上期望的姿态。图3给出了飞行器的一致性跟踪误差曲线图,可以看出在有限时间内误差能够收敛到充分小。图4展示了自适应律中的估计参数随时间的变化曲线。用总体跟踪误差来对比本文提出的有限时间命令滤波控制方案和文献[17]提出的有限时间动态面方法以及文献[16]提出的自适应动态面方法的性能,图5可以看出本文所涉及的控制方案和有限时间控制方案都能够实现有限时间收敛,但是本文提出的方案有更好的暂态性能和更小的稳态误差。

图4 ,i=1,2,3的响应曲线Fig.4 The response curves of ,i=1,2,3

图5 不同控制算法下的OTE轨迹Fig.5 The trajectories of OTE under different control algorithms
5 结束语
本文基于命令滤波反步方案构造了自适应有限时间控制器,成功解决了飞行器编队的分布式姿态跟踪控制问题,尽管系统中存在额外干扰和未知的惯性矩阵。在所提出的方案中,有限时间命令滤波解决了存在于反步设计中的计算爆炸问题,并且保证了飞行器系统的有限时间收敛速率。针对系统中未知的惯性矩阵和额外干扰,神经网络结合自适应方法能够很好地处理。误差补偿机制的建立弥补了滤波误差,保证了较小的静态误差和较好的跟踪性能。证明了总体跟踪误差能够在有限的时间内收敛到期望的原点的邻域范围内。通过仿真可以看出闭环系统有很好的收敛性能和抗干扰能力。

