无人机横侧向自抗扰飞行控制律设计

赵大海

（中国运载火箭技术研究院，北京100076）

1 引 言

无人机在飞行过程中，其横侧向运动较纵向运动有更强的耦合性，且在受到干扰后更易偏离预定轨迹，所以无人机的横侧向控制律设计是无人机飞行控制系统设计的重点，也是难点。

针对无人机横侧向运动的特点，主要有以下几种设计方法：

（1）增益调参控制［1-2］：它是一种应用经典控制理论来设计飞行控制系统的方法，在飞行全包线内，将飞机运动模型中的几个特定的飞行状态线性化，对每个特定飞行状态进行控制器设计。然后再将不同状态点的设计综合起来。

（2）动态逆控制［3-5］：这种控制方法的基本思想是利用全状态反馈将非线性系统转化为线性系统，即得到输入与输出成线性关系的系统。因此又称作非线性的反馈线性化方法。

（3）反步（Backstepping）控制［6-7］：该方法的基本思想是通过选取李氏函数，再用系统的一些状态去控制其他状态（避免在采用动态逆控制时抵消有用的非线性信息）的同时补偿不确定性的影响，最终得到稳定控制律。

（4）鲁棒控制技术［8-9］：鲁棒控制中最常用的两种方法为H∞控制和μ方法。H∞控制在处理非结构不确定性系统时是精确的，而对于结构不确定性系统具有保守性。μ方法可以克服这方面的缺点，在获得鲁棒性的同时得到较好的控制稳定性。

（5）神经网络控制［10-11］：这种控制方法有着很强的适应性，可以充分逼近无人机非线性的运动系统，是设计高度非线性系统和严重不确定系统控制方法的有效手段。

本文针对无人机横侧向强耦合、参数摄动以及风干扰等飞行特点，利用基于扩张状态观测器（Extended State Observer，ESO）、跟踪微分器（Tracking Differentiator，TD）、非线性状态反馈控制律（Nonlinear Law State Error Feedback，NLSEF）的自抗扰控制（Active Disturbance Rejection Control，ADRC）［12］来对无人机进行横侧向控制律设计，解决滚转及偏航运动的强耦合以及未知扰动源问题，改善系统响应的动态特性，提高系统鲁棒性。

2 无人机横侧向动力学模型

无人机横侧向动力学模型的建立是在以下假设下进行的：

（1）认为飞行器不仅是刚体，且质量为常数；

（2）假设地面为惯性参考系；

（3）忽略地球曲率，即把地球看作平面；

（4）假设重力加速度不随飞行高度而变化；

（5）假设机体轴系中OX轴，OY轴处于飞行器的对称平面内，因此惯性积Ixz、Iyz等于零。

根据给定的坐标系定义［13］，建立机体坐标系中相应的横侧向动力学模型：

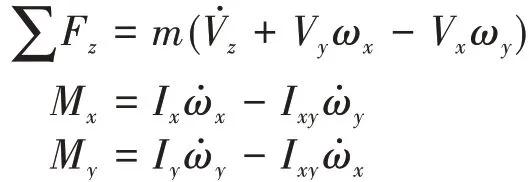
依此得到动力学模型：

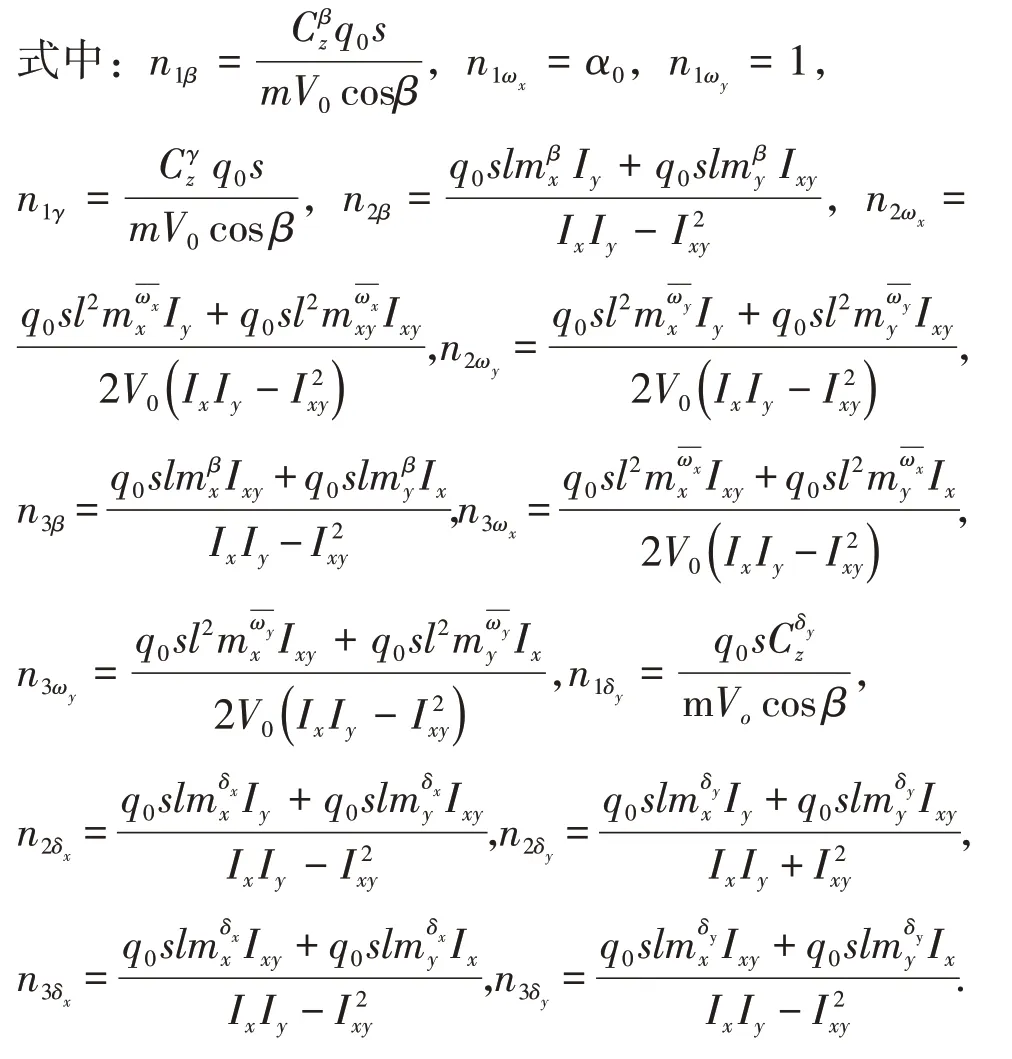
其中：q0=为自由流的动压，S为机翼面积，l为飞行器的特征长度。

3 无人机横侧向解耦控制模型

3.1 动态耦合特性分析

在进行飞行控制律设计之前，有必要分析无人机横侧向运动的耦合性。为分析舵偏对各姿态角的耦合影响，现取δx=1°、10°、20°，δy=0°和δx=0°，δy=1°、10°、20°进行仿真分析。假设无人机做Ma=0.9，H=11000m，V0=266m/s，α0=3.623°的倾斜转弯运动。仿真结果如图1、图2所示。

从图中可以看出舵机偏转对无人机横侧向姿态角的耦合影响，方向舵偏转时会引起滚转角的偏转，副翼偏转时也会引起偏航角的偏转。舵偏影响姿态角控制，姿态角又会影响无人机航迹曲线，所以在进行横侧向控制律设计时，必须考虑舵偏的耦合影响。

不仅舵偏会对各姿态角产生耦合影响，滚转与偏航角之间也会存在耦合影响。在无控输入的情况下，设定ωx、ωy的初始值分别为10°/s，0 和0，10°/s，仿真分析由此引起的其他状态变量的响应曲线。仿真结果如图3、图4所示。

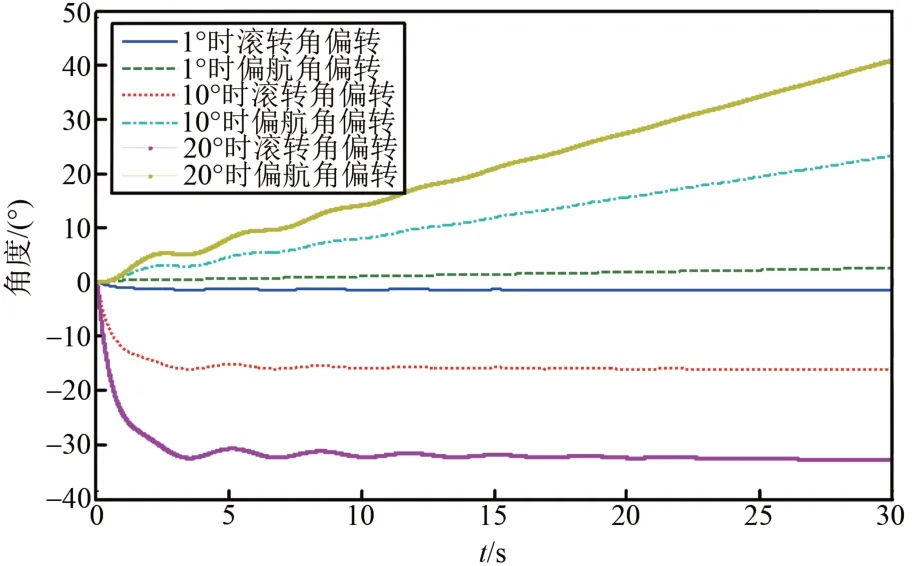
图1 δx取不同值，δv取0时的姿态角响应Fig.1 The response of attitude angle when δx take different values and δv take 0

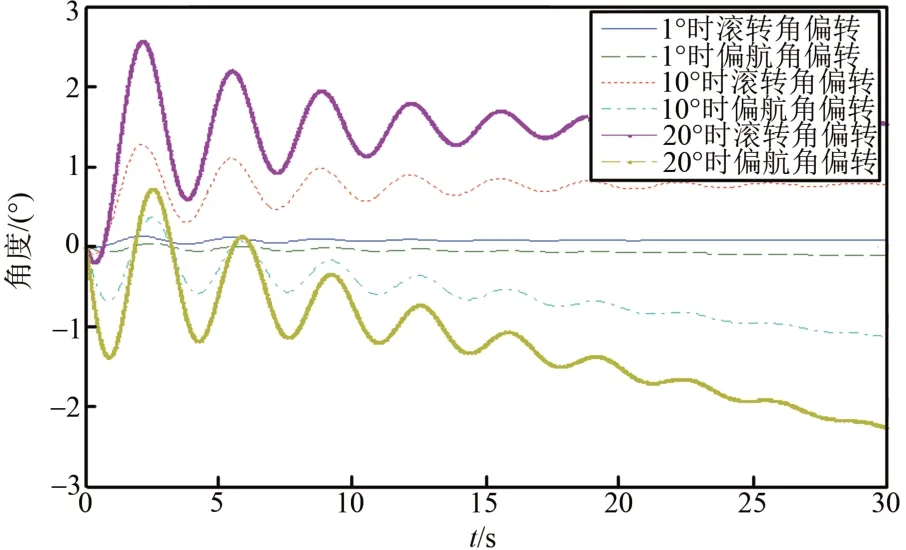
图2 δv取不同值，δx取0的姿态角响应Fig.2 The response of attitude angle when δv take different values and δx take 0

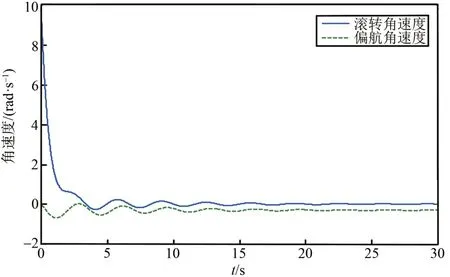
图3 ωv取0的姿态角速度响应Fig.3 The response of attitude angle velocity when ωv take 0

由仿真结果看出，滚转角和偏航角之间存在很强的耦合，两通道间的耦合累积效应会导致无人机失稳，因此在进行无人机横侧向控制器的设计时，必须要有鲁棒性更好的解耦控制器。

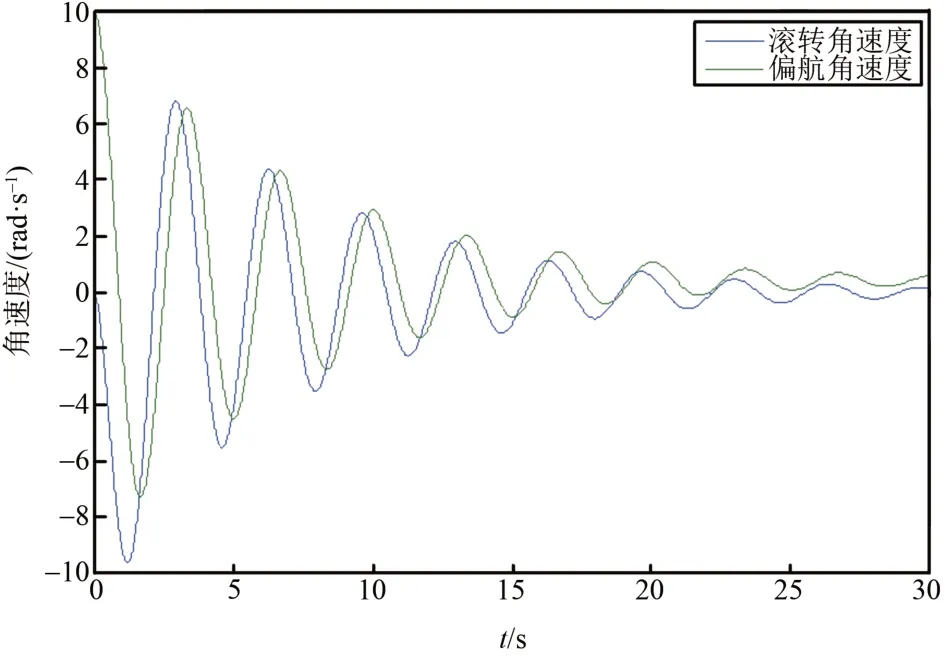
图4 ωx取0时的姿态角速度响应Fig.4 The response of attitude angle velocity when ωx take 0

3.2 解耦控制器设计

基于以上的无人机横侧向动力学模型，为便于控制律的设计和分析，建立无人机横侧向的解耦控制模型为：

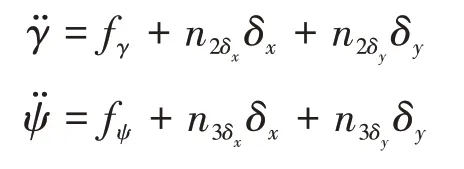
其中：

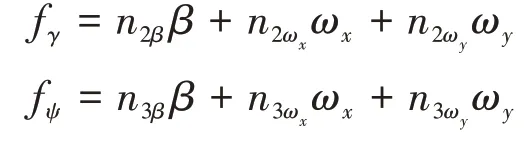
令

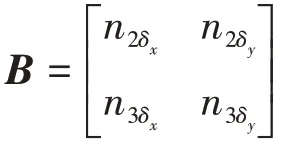
引入虚拟控制量U，

则横侧向动力学方程可改写为：

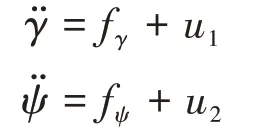
根据以上转换关系，无人机横侧向系统由多输入多输出系统变为单输入单输出系统，即输入u1，u2与输出γ，ψ之间被完全解耦。只要B可逆，实际控制量可由虚拟控制量求出。

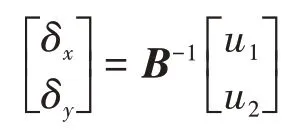
基于自抗扰的无人机横侧向解耦控制原理图如图5所示。其中，γ0为输入滚转角，γ为实际输出滚转角；ψ0为输入偏航角，ψ为输出偏航角。

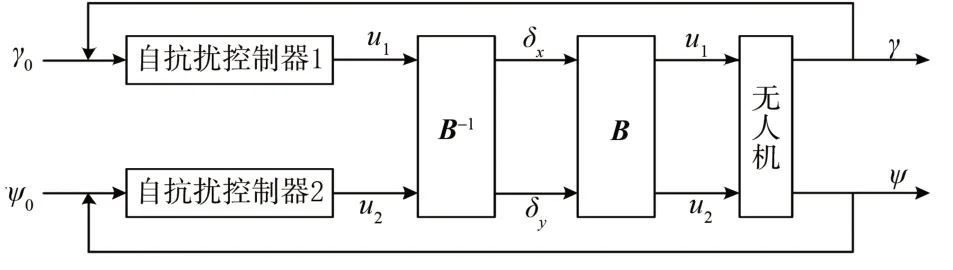
图5 解耦原理图Fig.5 Decoupling schematic diagram

4 自抗扰控制器设计

无人机滚转角通道ADRC设计结构图如图6所示，其中γ01为γ0的跟踪信号，起到安排过渡过程的作用，γ02为γ0的微分信号；u0为误差信号e1、e2的非线性组合。z1、z2、z3分别为ESO 对γ的跟踪信号，微分信号及对系统总扰动的估计信号；z3和u0相减构成控制信号u；偏航角通道采用相同的设计。

图6 自抗扰控制器Fig.6 Active Disturbance Rejection Control

4.1 TD设计

利用文献［12］提出的最速跟踪微分器，为本文的研究对象提供微分信号并安排过渡过程，其算法如下：

式中：fhan（·）为非线性函数，详见文献［12］。根据安排过渡过程的快慢，取参考值r=0.2，h=0.1。

4.2 NLSEF设计

针对本文研究对象，利用文献［12］中给出的算法设计：

根据各参数实际作用，取参考值：

α0=0.75，α1=1.5，β0=2000，β1=100。

4.3 ESO设计

针对文章研究对象，构建如下扩张状态观测器：

式中：βesoi＞0（i=1，2，3），α1=0.5，α2=0.25。fal(.)函数的定义具体见文献［12］。偏航和滚转通道使用相同结构的ADRC 控制器。根据文献［12］取参考值：βeso1=100，βeso2=3000，βeso3=15000。

4.4 基于遗传算法的控制参数优化

本文以文献［12］中给定的方法确定NLSEF及ESO 中参数的初值，即β0=2000，β1=100，βeso1=100，βeso2=3000，βeso3=15000。以输出响应的时域指标为判定准则，应用遗传算法对以上控制参数进行优化，流程图如图7。

最后优化得到结果为β0=2350，β1=110，βeso1=100，βeso2=3300，βeso3=15625。

图7 参数优化流程图Fig.7 Flow chart of parameter optimization

5 数字仿真

本文假设无人机做Ma=0.9，H=11000m，V0=266m/s，α0=3.623°的倾斜转弯运动。将设计好的自抗扰控制器应用到无人机的横侧向运动控制中。进行模拟仿真，仿真分析分为两个部分：

（1）同时给偏航通道和滚转通道输入单位阶跃信号，比较参数拉偏与未拉偏，加干扰与未加干扰下ADRC与PID控制的有效性、鲁棒性及稳定性。

（2）模拟无人机的倾斜转弯动作，在转弯过程中，受到阵风干扰。

5.1 针对参数摄动和外加干扰的仿真分析

首先，进行气动参数未拉偏，未加干扰的横侧向控制系统仿真分析。其次，针对风洞试验所获得的气动数据，为了分析系统的有效性、鲁棒性和稳定性，对气动数据进行拉偏，并进行相应的的仿真分析。最后，对无人机模型加干扰，进行加干扰后的系统仿真分析。本文在相同的外加干扰下，同时进行ADRC 和PID 控制的仿真，外加干扰信号为ω(t)=sin(pi*t)+rand。仿真时的输入信号为单位阶跃信号。

图8～9为采用传统PID控制的无人机滚转角与偏航角响应。

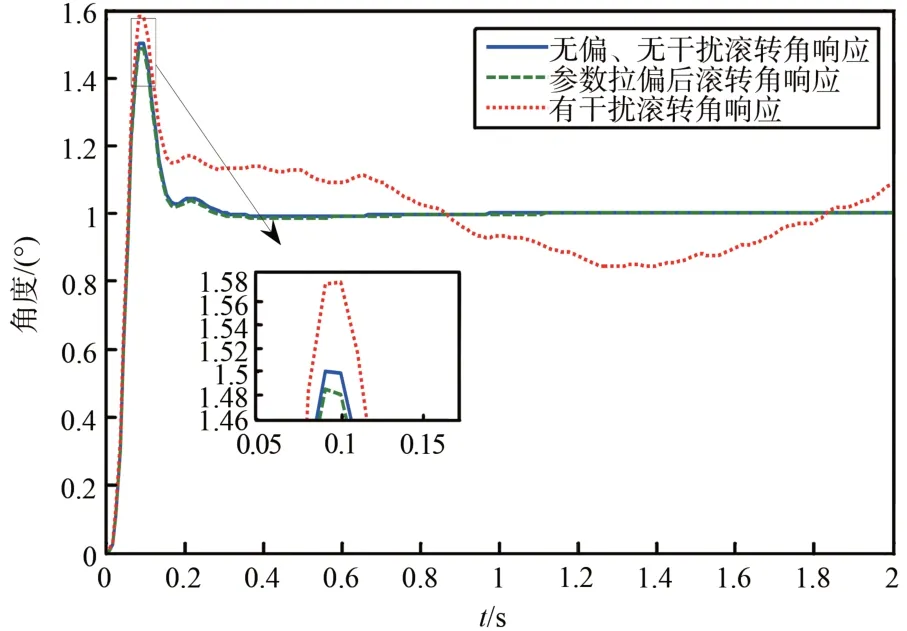
图9 不同情况下偏航角响应曲线Fig.9 Yaw angle response curve under different conditions

从图8～9可以看出，参数拉偏后的滚转角与偏航角的响应曲线与未拉偏的响应曲线大致重合，说明传统PID 控制对参数的不确定性具有一定的抑制作用。但是在加了干扰后，偏航角与滚转角的响应曲线发散，表明在ω(t)=sin(pi*t)+rand 的干扰作用下，传统PID 难以满足性能指标要求。

图10～11采用自抗扰控制器的无人机横侧向运动仿真结果。

图10 不同情况下滚转角响应曲线Fig.10 Response curve of roll angle under different conditions

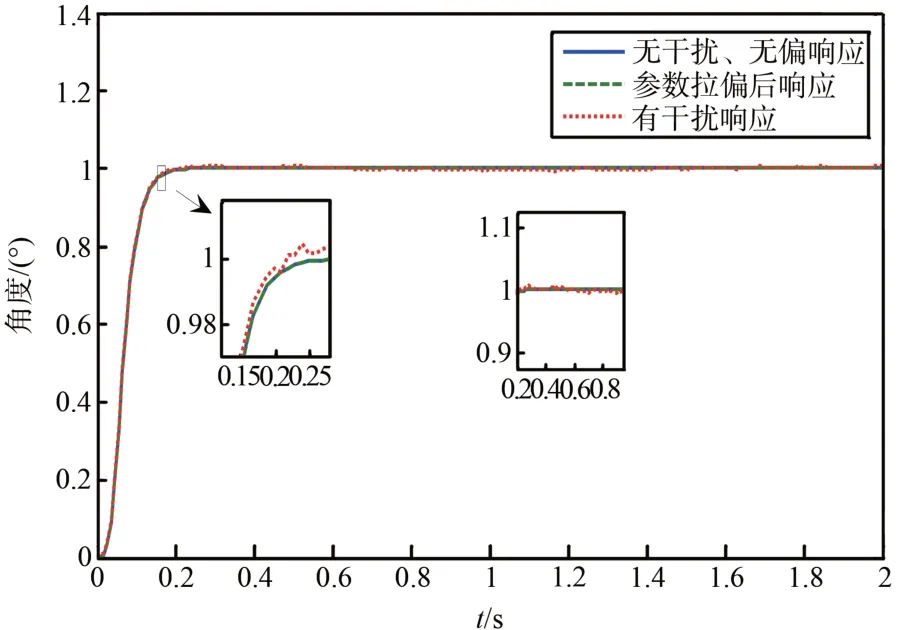
图11 不同情况下偏航角响应曲线Fig.11 Response curve of yaw angle under different conditions

由自抗扰飞行控制系统的仿真结果可以看出，无论是在参数拉偏还是加干扰的情况下，都可以得到较理想的滚转角与偏航角的响应曲线。采用ADRC 控制器的过渡过程时间约为采用PID控制的50%，几乎无超调，无振荡，而且在外加干扰下仍能较好的完成控制任务。

下面对不同情况下的PID控制与ADRC的仿真结果做比较。图12～13为参数无拉偏，未加干扰的情况下的ADRC与PID控制仿真结果。

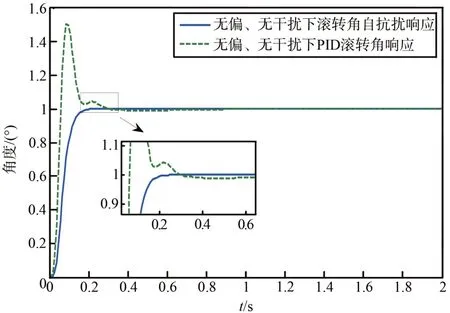
图12 不同控制器下的滚转角响应Fig.12 Response of roll angle under different controllers

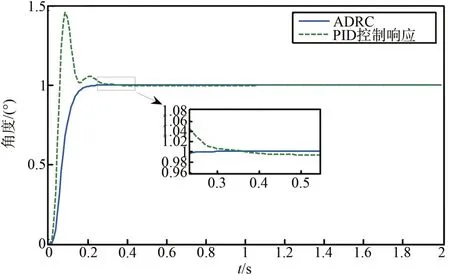
图13 不同控制器下的偏航角响应Fig.13 Yaw angle response under different controllers

在图12～13中可以看出ADRC 相对于PID 的优越性，无论是过渡过程时间、超调量、振荡次数，ADRC 控制都优于传统PID 控制。表明ADRC 较传统PID 控制有更好的跟踪特性与动态性能，同时也显示了自抗扰控制技术对强耦合及存在干扰条件下的无人机横侧向控制的有效性。

下面在有干扰的情况下进行仿真分析。从图14～15中可以看出，在加了干扰后，采用ADRC 控制器的横侧向姿态角的响应仍然具有良好的动态特性，而传统PID 控制下的响应则难以满足性能指标。表明ADRC控制具有较强的鲁棒性。

图16～17为系统总扰动和ESO 对总扰动的估计。从图中可以看出总扰动信号具有较大峰值，ESO 在一定程度上较好的观测了扰动信号，使ADRC 控制器很好的抵消了扰动对系统的影响，增强了鲁棒性。

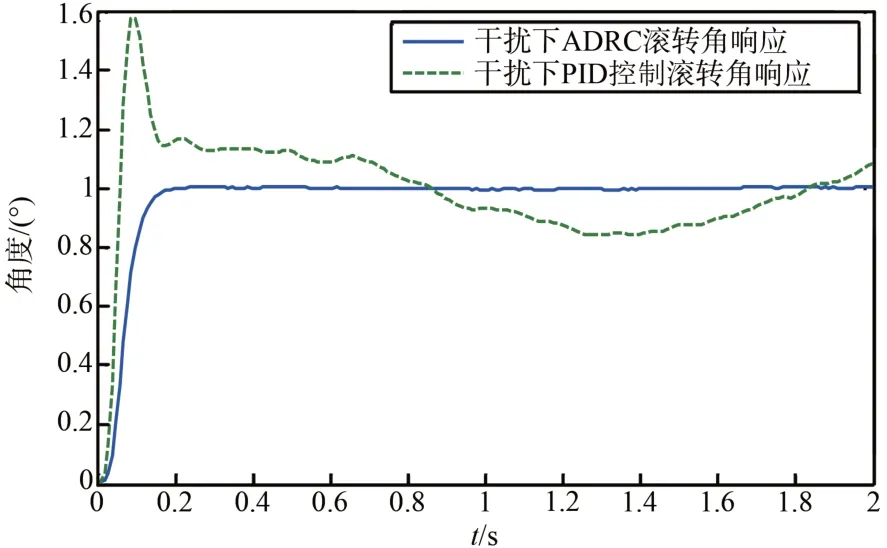
图14 有干扰情况下滚转角响应Fig.14 Response of roll angle in case of interference

图15 有干扰情况下偏航角响应Fig.15 Yaw angle response in case of interference

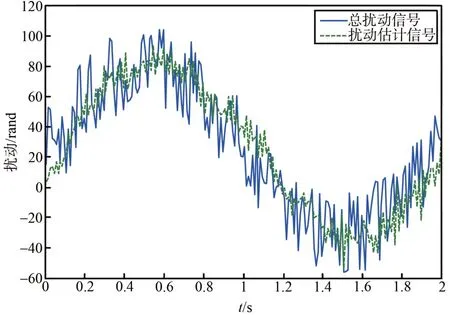
图16 滚转角通道扰动Fig.16 Roll angle channel disturbance

5.2 倾斜转弯时受到阵风干扰的仿真分析

其中滚转角偏转10°，偏航角偏转0°，阵风干扰信号值为10的脉冲信号，仿真结果如图18所示。

图18显示，在受到阵风干扰后，ADRC 下滚转角响应的超调量大约是PID 控制下的25%，过渡过程时间约为PID 控制的30%。表明在阵风干扰后，ADRC 比传统PID 控制具有更好的动态特性，同时具有较强的鲁棒性。

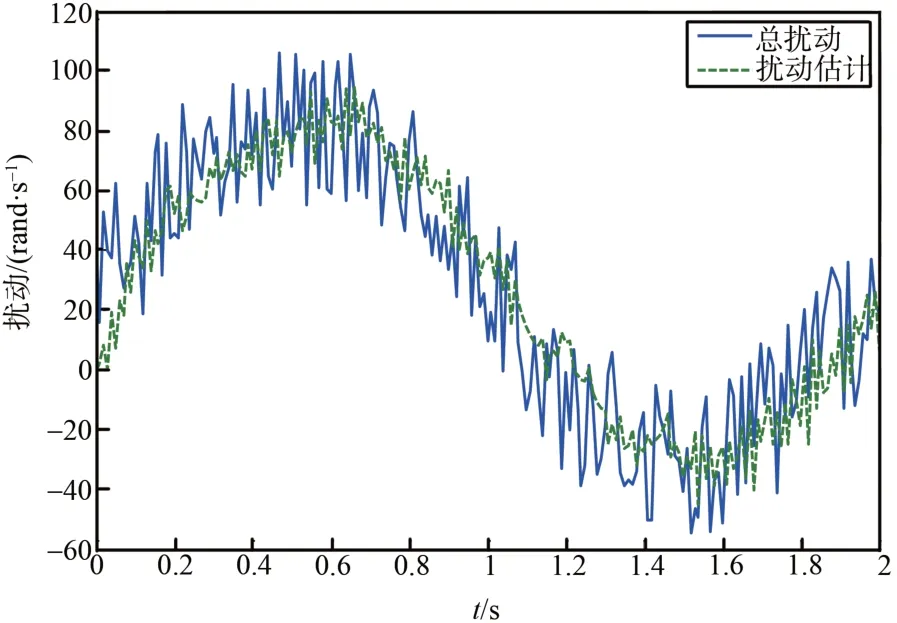
图17 偏航角通道扰动Fig.17 Yaw angle channel disturbance

图18 阵风干扰下，不同控制方式仿真结果Fig.18 Simulation results of different control modes under gust interference

6 结束语

本文将ADRC 控制技术应用到无人机的侧向耦合控制系统设计中，相应进行了横侧向动态耦合特性分析，自抗扰控制律设计分析及控制参数优化，并与传统PID 控制的无人机横侧向控制系统进行比较分析。无论是在无干扰，参数无拉偏还是在有干扰，参数拉偏的情况下，ADRC 都较传统PID控制具有更好的动态特性。且在参数拉偏和受到阵风干扰的情况下，ADRC 具有更好的鲁棒性。这表明ADRC 应用到无人机横侧向控制律的设计中，在得到良好动态特性的同时，也可获得很好的鲁棒性。