基于主动抗扰反步法的三维超低空空投飞行控制

苏子康，程遵堃，王宏伦

（1.南京航空航天大学自动化学院，南京211106；2.北京航空航天大学自动化科学与电气工程学院，北京100191）

1 引 言

货物低空空投系统因其快速的投放性能、无可替代的投放机动性、较高的投放精度、较大的远程投放能力、极强的环境适应性，已经广泛地应用于军事和民用的诸多领域［1-3］，如紧急救援投放，物资投递，森林灭火以及快速军事部署等［4-6］。

运输机超低空重装空投任务通常要求运输机在非常低的飞行高度（3～10m），以较低的飞行速度（0.20～0.25 马赫）完成投放过程［1，4-5］。然而，运输机的质量、重心和转动惯量都必然会因为货物在机舱内的移动和瞬间投放而受到明显影响。这些空投中的干扰会对飞行系统造成不可忽视的冲击，更严重的还有可能会影响空投的稳定，甚至造成空投事故。超低空空投过程中较低的飞行速度和高度会对飞行控制系统带来一些不可避免的问题：（1）低速低空带来的气动摄动和地面效应会随着高度的降低变得越来越明显［4］；（2）货物在货仓内连续移动和瞬间投放会对运输机飞行动态造成强烈的影响［5］；（3）超低空空投过程中不可避免的气流扰动（如阵风等）也会对飞行控制的抗干扰性能构成挑战［7-8］。低空空投过程中的扰动可以分为两大类：一种是内部扰动，即由货物移动和投放引起的运输机动态扰动；一种是外部扰动，如由地面效应引起的气动参数摄动和气流扰动对飞机动态的扰动。重装货物的移动，尤其是在出舱投落的瞬间，会对运输机的气动转矩、重心位置及转动惯量造成显著影响。而地面效应和气流扰动会对运输机的气动力和气动转矩造成无法忽视的影响。超低空重装空投特定的任务和工作环境要求其飞行控制器必须具有较好的跟踪控制精度和抗扰动性能。

目前，不少研究聚焦于飞行器纵向的二维空投控制器设计。文献［9］基于线性化的运输机空投纵向动力学模型，设计了L1 自适应空投纵向控制器。文献［10］针对运输机空投纵向非线性动力学模型，设计了基于滑模变结构理论的空投飞行控制器，以提升空投控制性能。基于反步法（Back-stepping，BS）的飞行控制方法也被应用于运输机二维空投控制研究［11］。为了增强空投飞行控制器的鲁棒性，基于干扰观测器的二维复合抗干扰结构引起了研究人员的注意［5，12-13］。然而，这些研究多集中于运输机纵向空投飞行控制设计，少有基于运输机6 自由度非线性模型而进行的空投飞行控制器研究。文献［14］建立了考虑风扰、地效和货物运动影响的运输机空投6 自由度模型，并设计了控制器，但并未针对超低空空投多重复杂扰动的特点，设计专门的抗干扰控制机制。

基于上述分析，本文针对运输机超低空空投6自由度非线性模型，开展三维非线性空投飞行控制方法研究。而运输机超低空空投6 自由度非线性模型的强耦合特性给控制器设计造成了一定困难［5］。但基于反步法的飞行控制器设计思路给三维空投非线性解耦控制提供了一种有效的途径［15］。此外，针对上述提到的抗干扰性能问题，本文借鉴基于干扰观测器的飞行控制器设计思路［16］，对飞行器各回路分别设计了一种有限时间收敛的非线性干扰观测器（Nonlinear Disturbance Observer，NDO）［17］，以实现对各回路集总干扰地准确估计。并在此基础上，提出了一种结合反步法和非线性干扰观测器的三维超低空空投抗干扰飞行控制器，以实现多重复杂扰动下超低空空投运输机的精确控制。

2 问题建模

考虑到实际空投情况，给出以下假设［5，14］：

假设1.运输机和货物均可视为刚体。

假设2.货物在机舱内的移动平行于飞机机身轴线。

假设3.所有飞行状态Vk，Xi，i=1，2，3，4 均可测量获取。

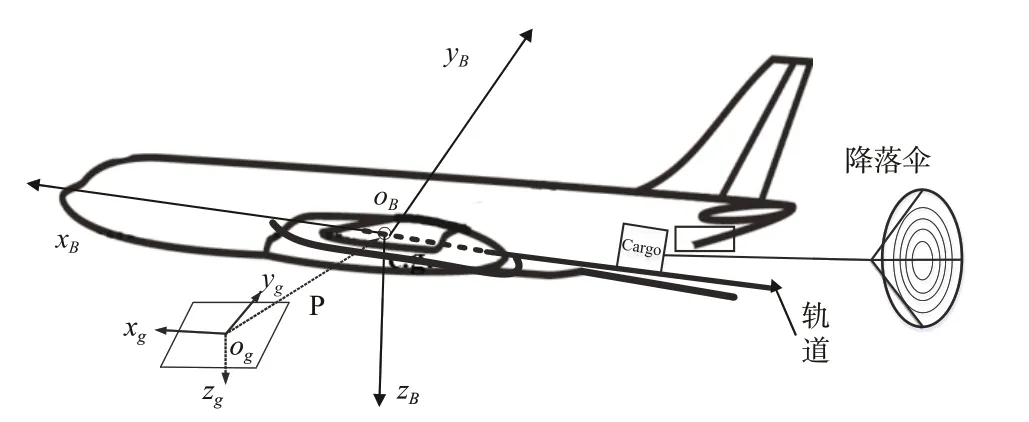
图1 运输机超低空空投过程示意图Fig.1 The transport aircraft airdrop process

运输机超低空空投示意图如图1。根据固定翼无人机6 自由度非线性模型，同时考虑气流扰动、地效和货物运动对运输机动态的影响，可建立运输机超低空空投6自由度模型如下［14，18］：

其中：c(·)=cos(·)，s(·)=sin(·)；m=ma+mc，mc，ma分别为货物和飞机质量；Vk为地速，p=[x y z]T为飞机质心位置，α，β为气流角，μ为速度滚转角，γ，χ为航迹角，ω=[p q r]T为角速率；Ii，i=x，y，z，xz为转动惯量，T为推力，L，D，C为升力、阻力和侧力；ℒ，ℳ，N 为三轴气动力矩；αK，βK为航迹系下的气流角，αw，βw为扰流引起的气流角扰动［15］；Δi，i=x，y，z和Δj，j=p，q，r为货物运动引起的沿机体的位置和交加速度扰动［14］；ΔgeV，Δgeχ，Δgeγ，Δgep，Δgeq，Δger为地面效应引起的各通道扰动［14-15，18］。

为便于控制器设计，以下对式（1）～（4）进行仿射非线性化处理。定义状态变量如下：

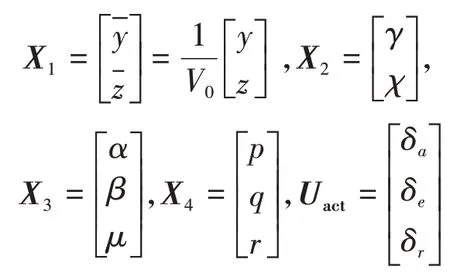
其中：V0为期望地速，此处也作为归一化变量；ρ，V，Q=0.5ρV2分别为大气密度、空速和动压。

通过模型变换，可得到仿射非线性模型：

其中，F1=[fy，fz]T，F2=[fχ，fγ]T，F3=[fα，fβ，fμ]T，F4=[fp，fq，fr]T；gy=G1(1)，gz=G1(2)，gχ=G2(1)，gγ=G2(2)，gα=G3(1)，gβ=G3(2)，gμ=G3(3)，gp=G4(1)，gq=G4(2)，gr=G4(3)；本 文 将fVk，Fi，i=1，2，3，4视为各回路集总扰动［18］。

3 基于主动抗扰反步法的三维空投飞行控制

本文需要设计一个三维低空空投轨迹跟踪控制器，以实现在多重复杂低空空投环境扰动下对给定飞行轨迹和速度指令的准确跟踪。采用反步技术，空投飞行控制器被分为轨迹回路、航迹回路、姿态回路、角速度回路和地速回路。基于反步设计，采用跟踪微分器（Tracking Differentiator，TD）［19］求取虚拟控制量的微分信号，解决微分爆炸问题。

定义跟踪误差向量和虚拟控制量如式（7）：

图2 基于BS-NDO的运输机超低空空投飞行控制Fig.2 The diagram of the proposed airdrop controller based on BS-NDO

其中，X*1为期望的横向、垂向轨迹指令，υ1，υ2，υ3分别为轨迹、航迹和姿态回路虚拟控制量。

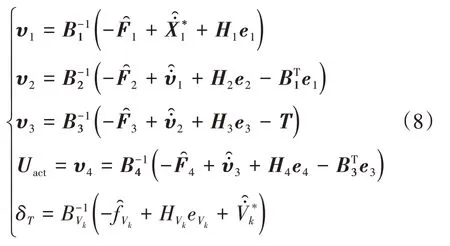
其中，Hurwitz 矩阵HVk，Hi，i=1，2，3，4 决定各回路

根据文献［17］，可分别对各飞行状态的微分方程设计有限时间收敛NDO如下：

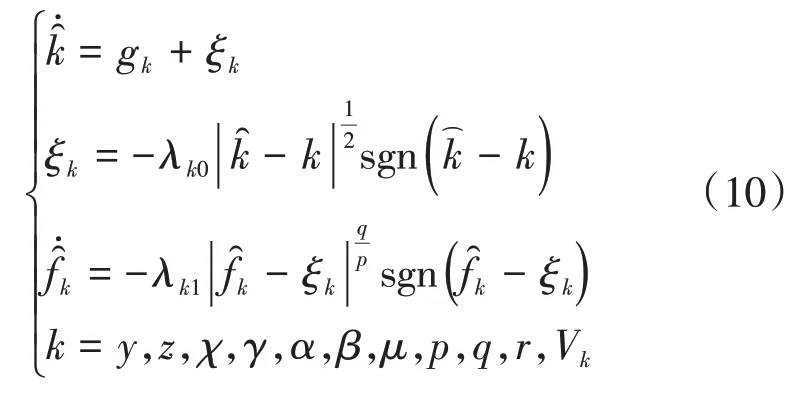
其中，k为系统飞行状态符号；为状态k的估计值；

基于反步控制理论[15]，设计超低空空投飞行控制器如式（8）：为集总扰动fk的估计值；p，q为Terminal吸引子设计参数［17］，λk0，λk1为滑模微分器设计参数，ξk是NDO 的内部辅助变量。

注1.根据文献［17］关于NDO 的证明分析，若fk为快变干扰，则NDO 的估计误差=-k和=-fk将在有限时间内收敛至包含零点的半球内，收敛过程振荡衰减，选择合适的参数λk0，λk1，可使得闭球半径足够小；若fk为快变干扰，近似有=0，则NDO的估计误差和将在有限时间内收敛至原点。

定理1.对于超低空空投6 自由度动态系统式（5）～（6），采用式（10）所示的干扰观测器和式（8）所示反步控制器，能够保证闭环控制系统稳定，同时使得各回路跟踪误差收敛。

证.控制器式（8）依赖于NDO估计的干扰fk，而NDO的估计动态特性也受控制器式（8）的影响。因此，在接下来的闭环稳定分析中，将同时考虑干扰估计误差和虚拟控制量微分信号的额估计误差。

选择如下的Lyapunov函数：

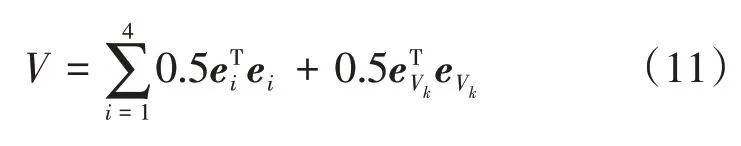
结合控制器式（8），可推得Lyapunov 函数关于时间的一阶导数为：

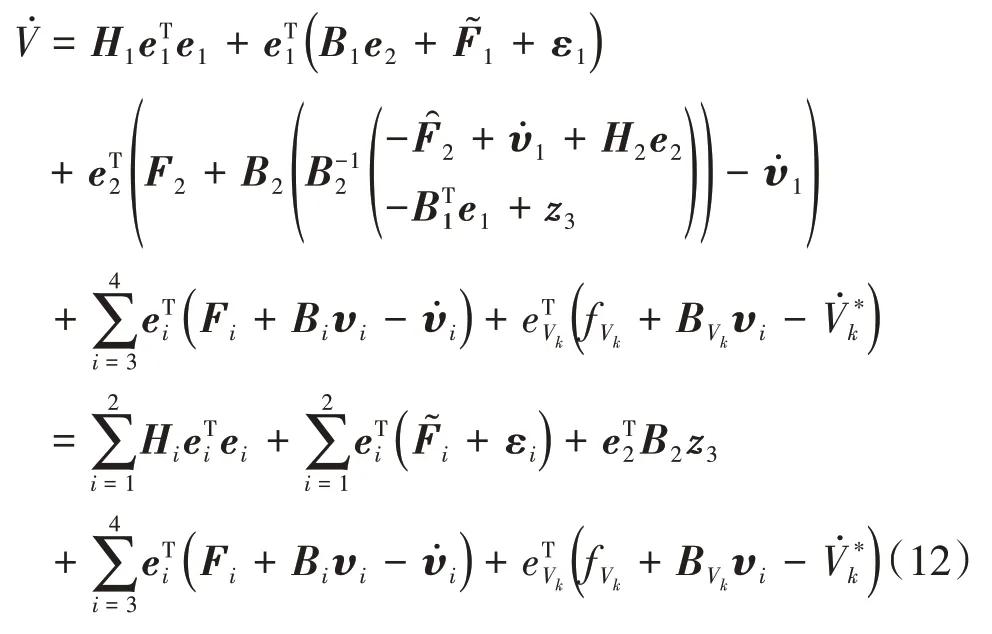
考虑到eT2B2z3=eT3T，进一步可以得到：

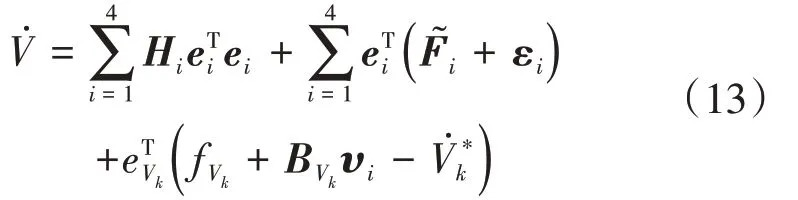
然后，可得：

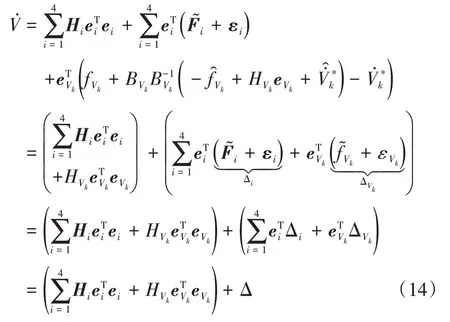
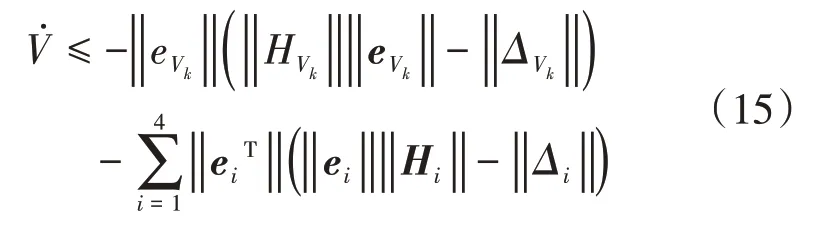
所以，当Hurwitz矩阵HVk，Hi，i=1，2，3，4选取足够大且NDO、TD 参数选取合适时，可以保证V˙＜0。而且，系统跟踪误差(e1，e2，e3，e4，eVk)将收敛至0。证毕。

4 仿真验证及分析

本节将基于运输机超低空空投6自由度动力学模型，对所提出的飞行控制器进行对比仿真，以验证其有效性。本文采用文献［20］的飞机气动参数作为研究对象运输机。为了对比的相对公平，本文选取同样基于干扰观测器控制结构的自抗扰控制（Active Disturbance Rejection Control，ADRC）［12］，与本文所提出的BS-NDO飞行控制器进行仿真对比。

设定超低空空投飞行条件为：飞行高度10m，飞行速度80m/s。所选择对比控制方法的控制参数如下：

（1）ADRC方法

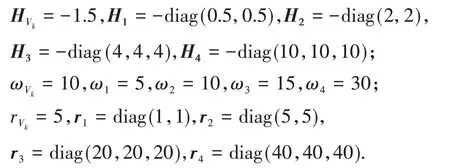
（2）本文所提出的BS-NDO方法

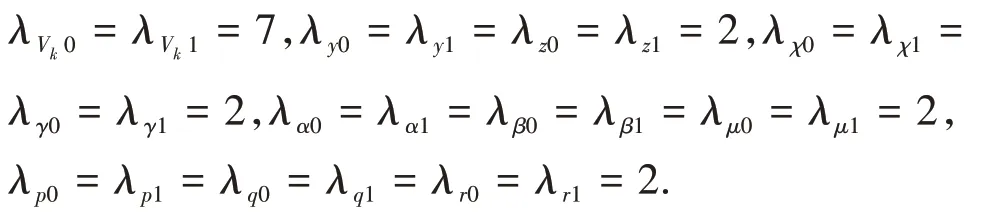
其他参数，如HVk，Hi，i=1，2，3，4 和TD 参数选取，与ADRC方法相同。

仿真环境设置如图3所示的半周期正弦风干扰，其在惯性系下三轴分量Wx，Wy，Wz如图所示。并假设地面效应对运输机气动参数影响为在其标称气动参数基础上，［-10%，10%］范围内的随机摄动。假设空投过程中，货物投放开始于t=20s，即货物在t=20s开始沿着机舱轨道滑动投放。

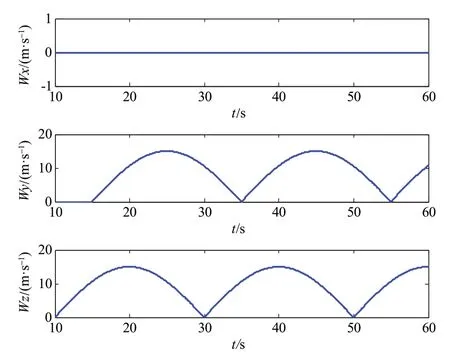
图3 仿真设置的超低空空投环境气流扰动Fig.3 Airflow disturbances during the low-altitude airdrop

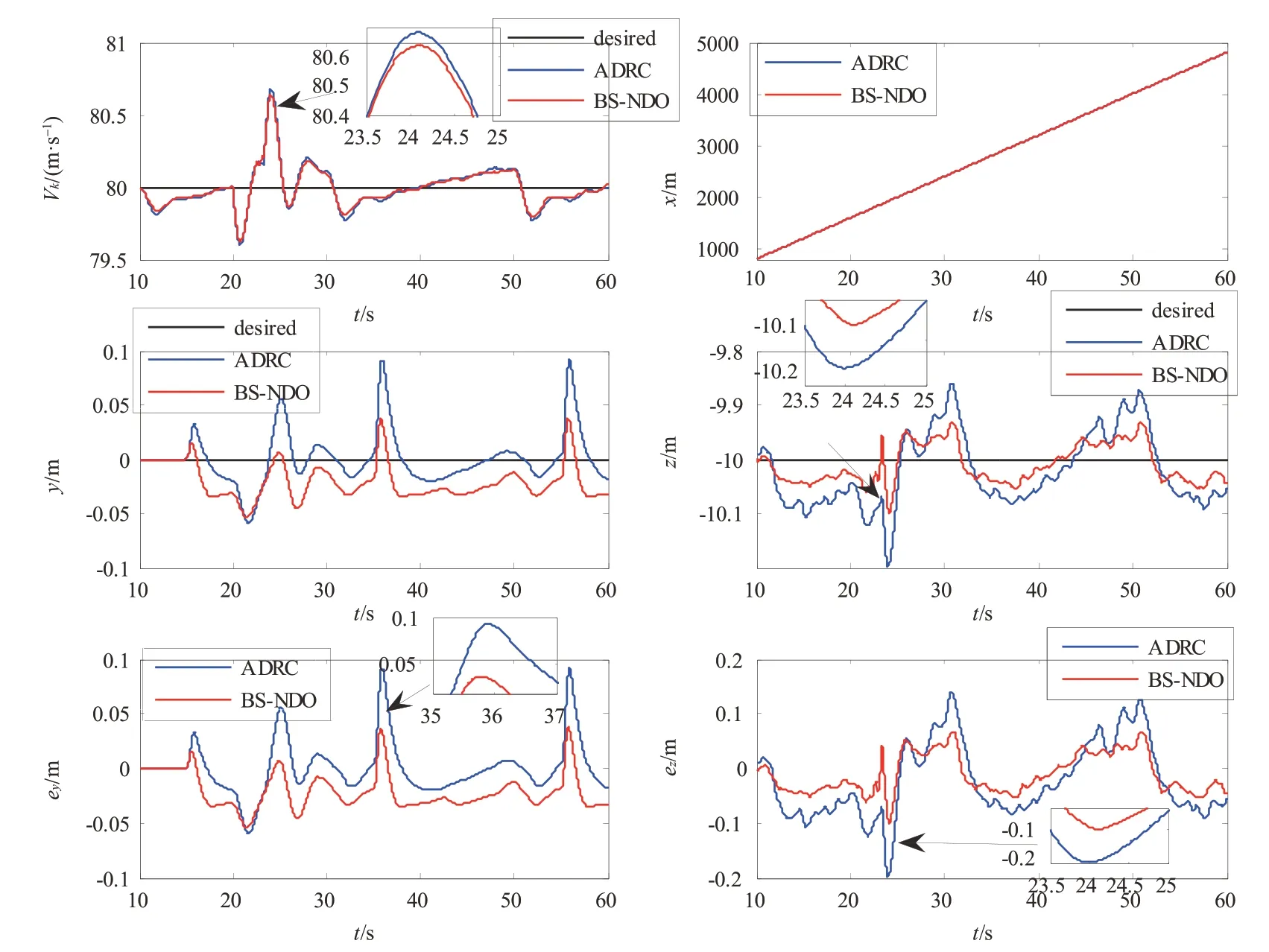
图4 地速、位置和位置跟踪误差仿真结果Fig.4 Results for velocity,positions and tracking errors

图5 气流角、欧拉角仿真结果Fig.5 Results for the airflow angles and Euler angles

BS-NDO 和ADRC 两种方法的相关仿真对比结果，如图4～6所示。图4为两种控制方法下地速、横/垂向位置及位置跟踪误差仿真结果。从图中可以看出地速跟踪和前向位置结果十分相似，这是由于其采用相同的、单独通道的地速控制器。BS-NDO方法控制下的横向位置y和垂向位置z更接近指令信号，其跟踪误差也较小，分别被限制在0.05m 和0.1m 以内。而ADRC 控制下的位置跟踪误差更大一些，分别在0.1m 和0.2m 以内。BS-NDO 最大跟踪误差相较于ADRC 减小了近50%。这也说明了本文提出的BS-NDO 超低空空投控制器具有更高的控制精度和更好的抗干扰能力。

图5为两种飞行控制方法对应的气流角（迎角、侧滑角）和欧拉角（滚转角、俯仰角和偏航角）仿真结果。由图可见，两种控制方法对应的气流角和欧拉角结果类似。图6给出的是BS-NDO 和ADRC 两种方法对应的控制输入量。由图可见，BS-NDO 部分控制量较ADRC 偏大，如升降舵偏角δE。这也是BS-NDO获得更高控制精度和较好抗扰性能而需要付出的控制代价。

综合上述仿真结果分析可知，本文所提出的BS-NDO 方法，在考虑气流扰动、地效和货物投放等多重复杂扰动下的超低空重装空投飞行控制方面，具有更高控制精度和较好抗扰性能。

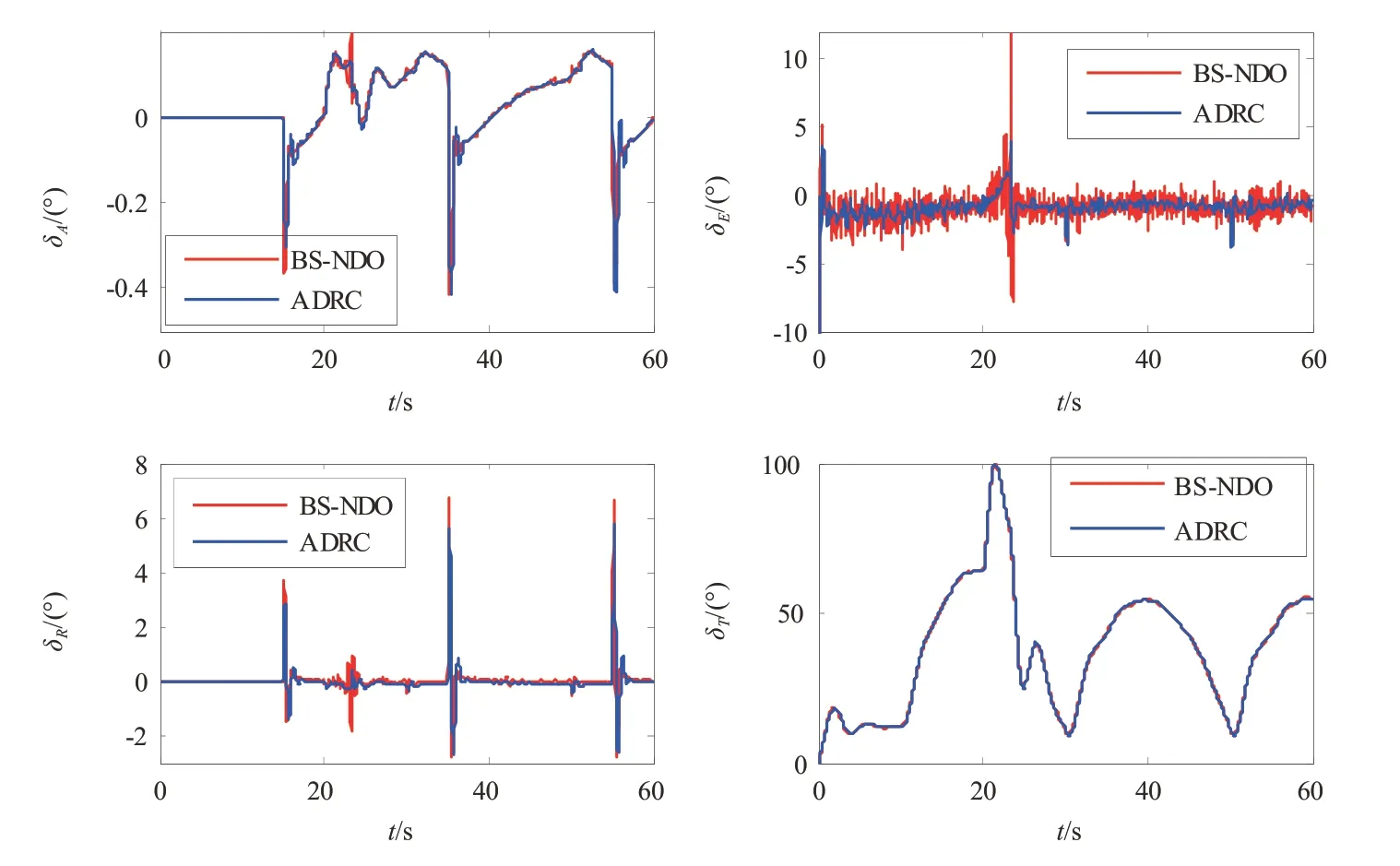
图6 控制输入量结果Fig.6 Results for control inputs

5 结束语

本文针对运输机超低空空投鲁棒飞行控制问题，提出了基于有限时间非线性干扰观测器的主动抗扰反步法的三维飞行控制方法。与现有文献中超低空空投控制方法不同，该方法是基于运输机超低空空投6 自由度模型而提出的三维主动抗扰飞行控制方法，能够保证运输机在风扰、地面效应和空投瞬时动态摄动等多重复杂扰动下实现精确轨迹跟踪飞行。仿真验证表明，本文所提方法具有较高的跟踪精度和较出色的抗干扰能力。本文所提方法对于运输机超低空空投建模与控制技术的研究具有一定参考价值，未来将针对超低空空投背景下飞行状态受严格约束的抗干扰飞行控制方法进行深入研究。