聚能装药破甲深度炸高不敏感性研究*
高 飞,王雨时,闻 泉,张志彪,王光宇
(南京理工大学机械工程学院, 南京 210094)
0 引言
聚能装药依靠炸药的爆轰使金属罩快速变形,形成一股能量密度高和方向性强的金属射流。实践表明,对于一定的聚能装药结构,其射流形成过程受炸高影响比较大。若炸高过低,射流得不到充分的拉伸会导致破甲效果差。若炸高过高,射流拉伸长度超过自身材料拉伸极限,就会断裂成多段,使破甲威力显著下降。郑平泰等[1]通过试验研究了不同炸高下铸铝药型罩聚能射流对混凝土的侵彻,从试验结果看,不同炸高下射流侵彻深度相差较大,对应炸高150~350 mm时侵深极差为157 mm。张向荣等[2]采用数值模拟方法研究了炸高对钨铜合金药型罩在空气中和水下聚能射流破甲深度的影响。马海洋等[3]采用数值模拟的方法研究了4种炸高下线型聚能装药破甲物理过程,发现聚能射流头部第一次断裂的位置并不是最佳炸高位置,最佳炸高为射流第一次断裂后的某个位置。目前研究不同炸高下聚能装药破甲威力的文献较多,但未见有文献研究如何通过改变装药结构来提高其破甲深度的炸高不敏感性。为了降低聚能射流破甲深度对炸高的敏感性,从而适用于多种复杂环境,设计出一种对炸高不敏感的聚能装药结构是很有必要的。
1 数值模拟
1.1 聚能装药几何模型及有限元模型
聚能装药结构如图1所示。装药为聚黑-2,密度1.688 g/cm3。装药直径Ф64 mm,装药部分全高85 mm。药型罩锥角60°,等壁厚1.3 mm,高49.6 mm,材料为低碳钢。壳体材料为尼龙。

图1 聚能装药结构
运用AUTODYN-2D软件对上述装药结构建立几何模型并进行网格划分。此聚能装药结构具有轴对称性,建立1/2模型。由于聚能射流成型过程中属于高应变和高应变率过程,故采用欧拉网格划分药型罩和靶板,炸药和壳体采用拉格朗日网格划分,炸药对药型罩的作用采用流固耦合方法。为防止应力在边界反射,除轴线外,在欧拉网格边界设定流出边界。
为减小计算量,将整个侵彻过程分为射流成型阶段和射流侵彻靶板阶段。在射流成型阶段,不考虑靶板的影响,计算域尺寸为155 mm×60 mm,计算域内填充材料,聚能装药有限元模型和网格划分如图2所示。图3为t=20 μs射流形态,此时射流即将到达靶板。为了建立直径100 mm、厚300 mm的45钢靶板模型,扩大计算域,取炸高为50 mm,如图4所示。在t=25 μs时炸药和壳体对射流作用已经结束,此时删除炸药和壳体。
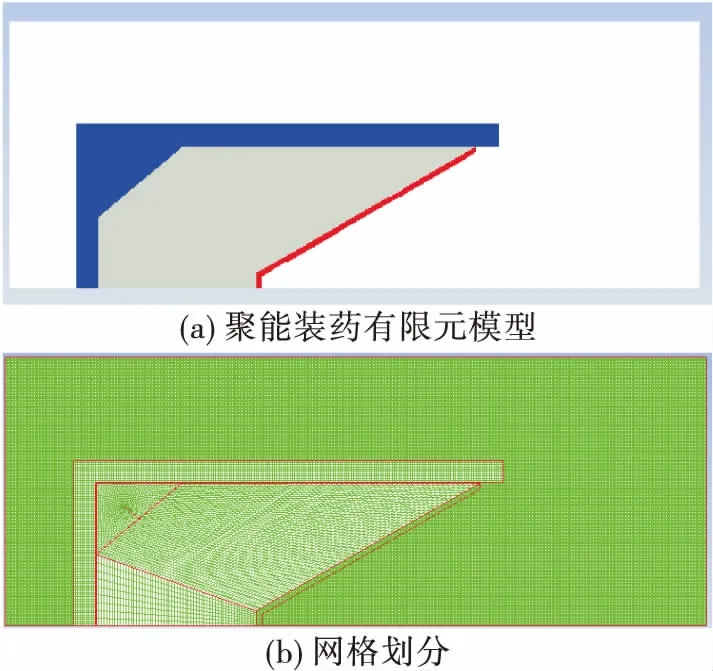
图2 聚能装药有限元模型和网格划分
1.2 材料模型与状态方程的选取
炸药装药选为聚黑-2,采用JWL材料模型和EOS状态方程来描述炸药的爆轰过程。低碳钢药型罩和45钢靶板材料模型为Johnson-Cook模型,状态方程均为Shock方程。尼龙壳体材料模型取为Von Mises模型,状态方程为Shock方程,且添加失效为静水拉伸临界压力。不同材料模型和状态方程中所选用的参数如表1~表3所列,其中药型罩材料1006低碳钢和壳体材料尼龙均采用AUTODYN软件材料库中的材料模型和状态方程参数。
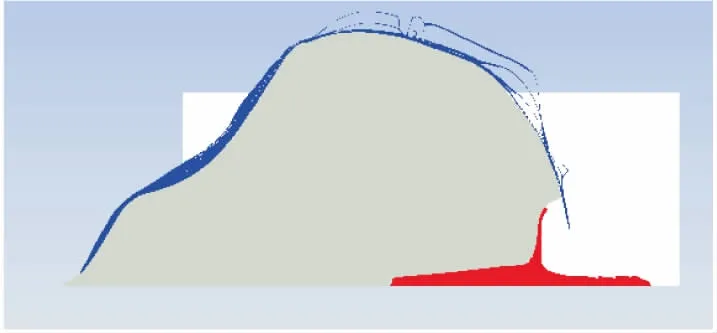
图3 射流成型阶段形态

图4 射流即将侵彻靶板阶段
表1 聚黑-2材料模型和状态方程参数[4]

密度ρ/( g·cm-3 )爆速D/( m·s-1 )C-J压力PCJ/GPa初始内能E0/GPa1.688830029.69.3JWL系数A/GPaB/GPaR1R2ωk852184.61.30.341
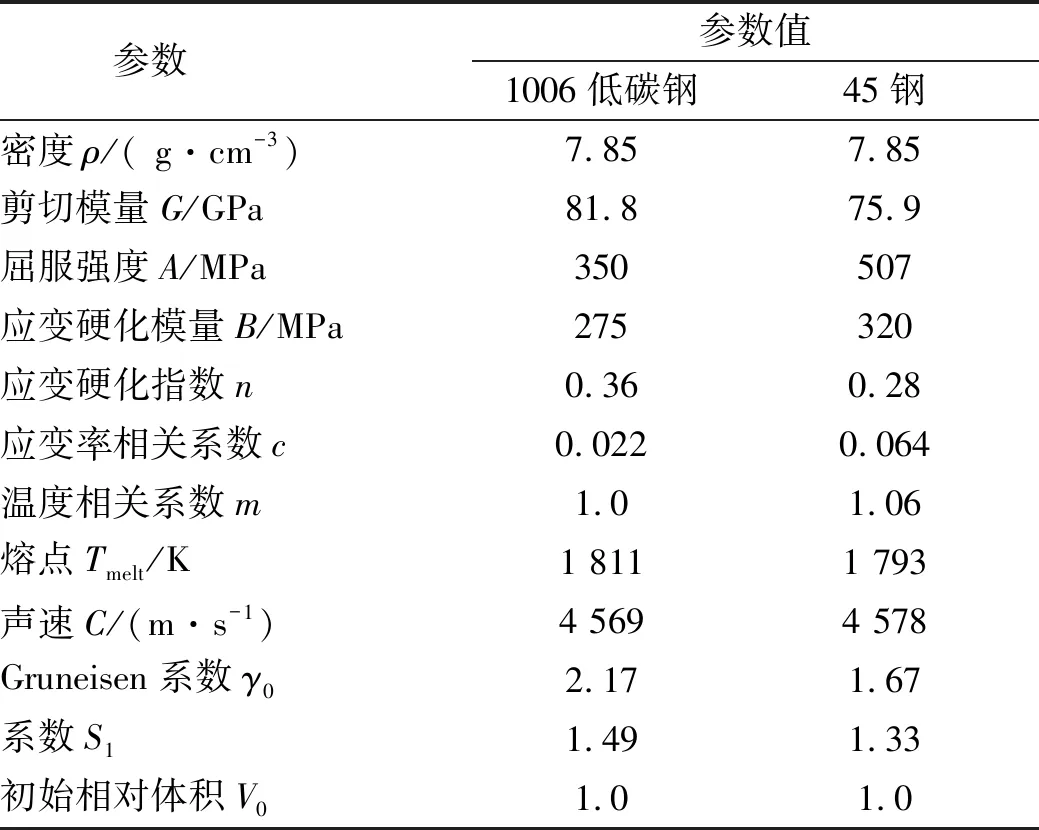
表2 1006低碳钢药型罩和45钢材料模型及状态方程参数[5]

表3 尼龙材料模型和状态方程参数[6]
2 计算结果分析
2.1 射流到达靶板时性能分析
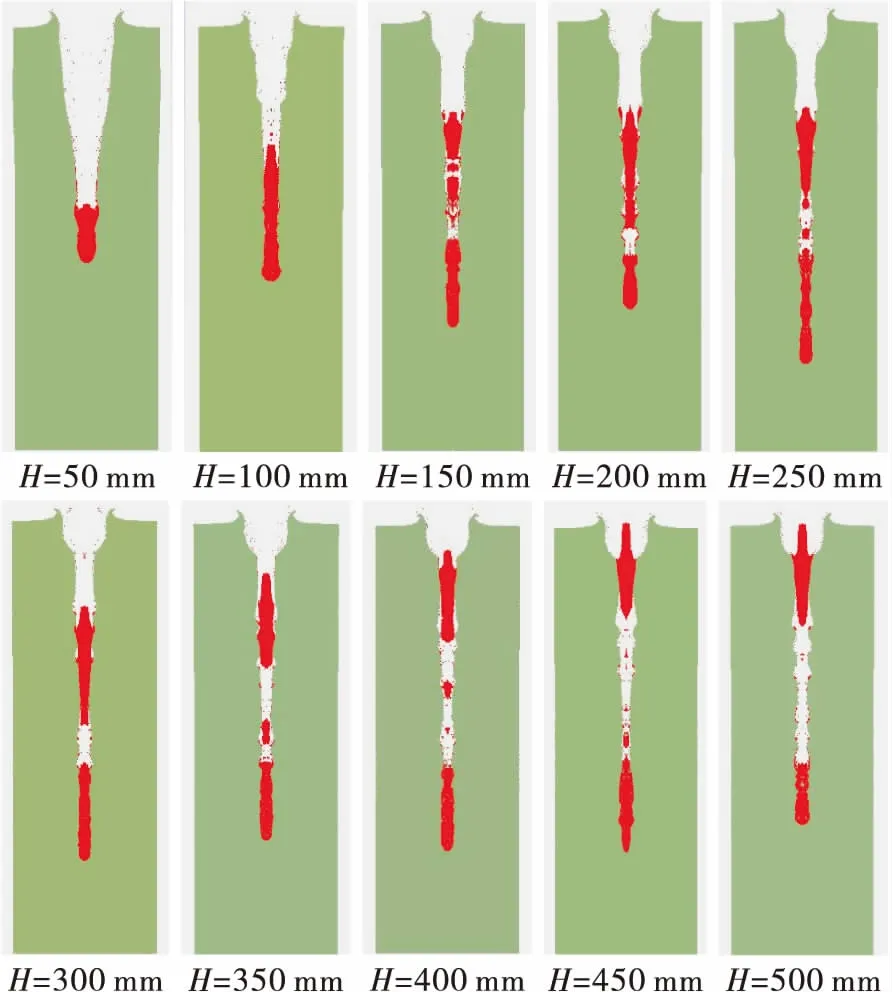
对射流头部即将运动至靶板时进行截图,不同炸高条件下射流运动至靶板时的形态如图5所示。表4列出了射流到达靶板时的参数。随着炸高的增大,射流轴向速度梯度的存在使射流被拉伸,当射流塑性失稳时就会断裂。从图5可看出,炸高H范围为50~100 mm时,射流得到充分拉伸且头部未发生断裂;炸高H=150 mm时射流到达靶板时头部颈缩,发生断裂;炸高继续增大时,射流头部多处发生颈缩和断裂。断裂的射流不能保持侵彻连续性,且断裂的射流粒子运动过程中会发生翻转和偏移,最终侵彻深度会降低。射流断裂的越早,则最佳炸高越小,最佳炸高下射流侵彻深度也会减小。若能通过改变装药结构使射流断裂的时间缩短,则不同炸高时射流侵彻深度极差就会减小,从而有利于提高聚能装药破甲深度的炸高不敏感性。
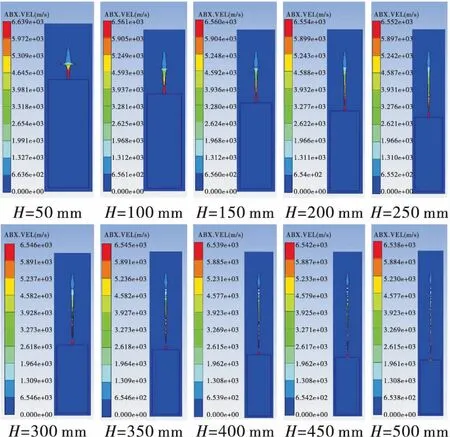
图5 不同炸高条件下射流运动至靶板时的形态
表4 不同炸高条件下射流到达靶板时的参数
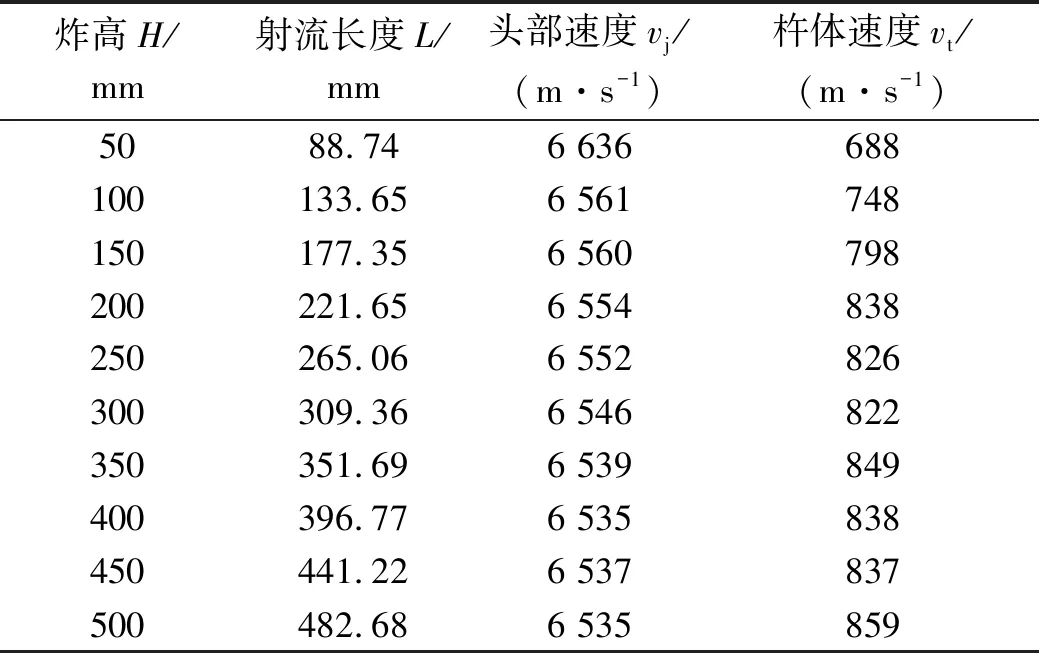
炸高H/mm射流长度L/mm头部速度vj /(m·s-1)杵体速度vt/(m·s-1)5088.746 636688100133.656 561748150177.356 560798200221.656 554838250265.066 552826300309.366 546822350351.696 539849400396.776 535838450441.226 537837500482.686 535859
从表4可知,随着炸高的增大,射流拉伸长度持续变大,射流头部速度有所降低,杵体速度有所增大。射流长度与侵彻能力成正相关,若能通过改变装药结构使射流头部速度和杵体速度的差值减小,则射流长度就会减小,不同炸高时射流侵彻深度极差减小,有利于提高聚能装药破甲深度的炸高不敏感性。
2.2 射流侵彻45钢靶板过程分析
图6为炸高H=150 mm时射流侵彻靶板过程,图7为炸高H=150 mm时射流侵彻深度h随时间t的变化曲线。
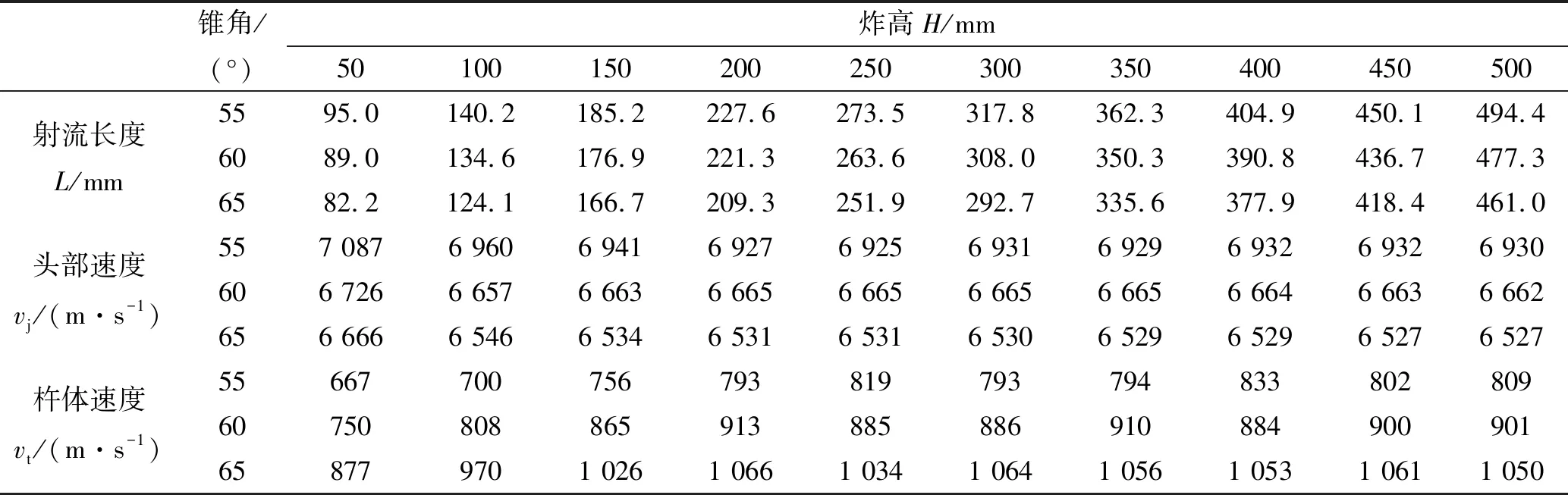
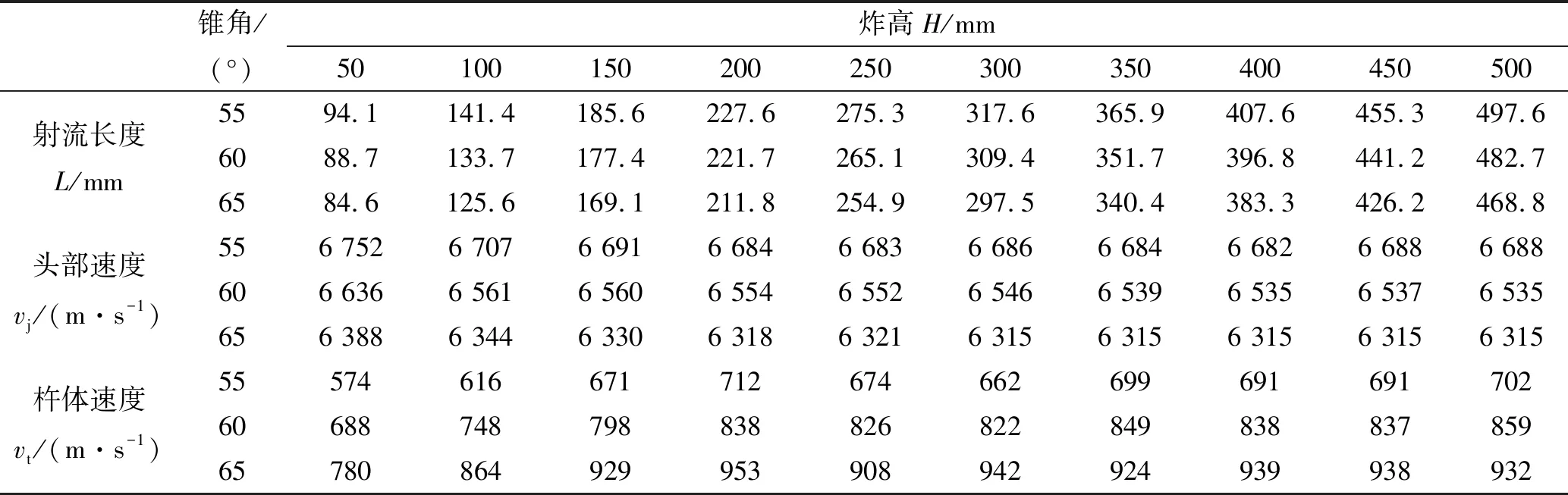
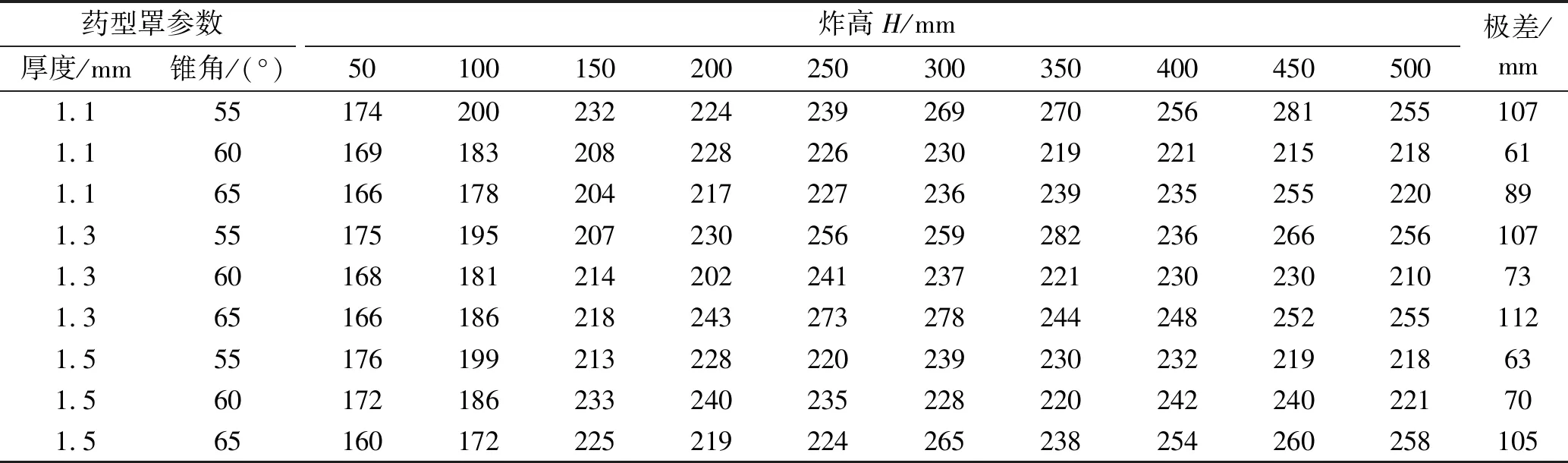
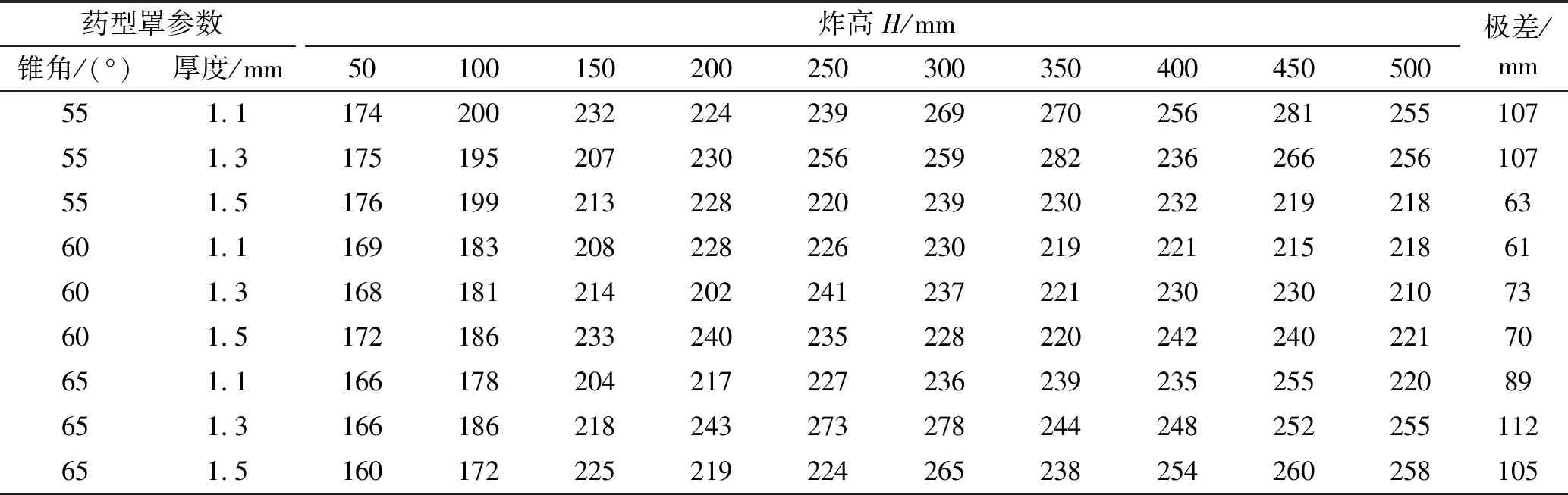
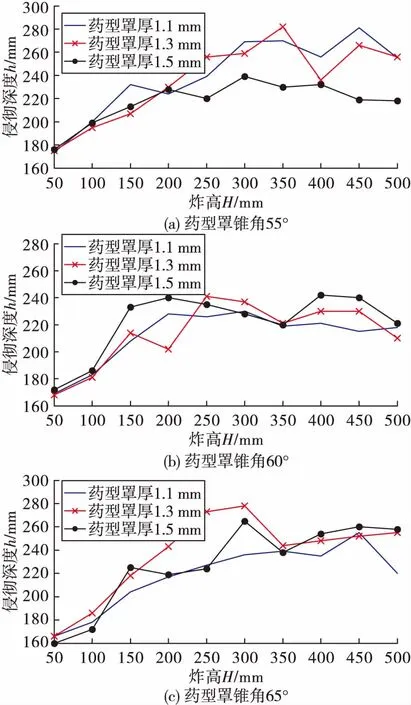
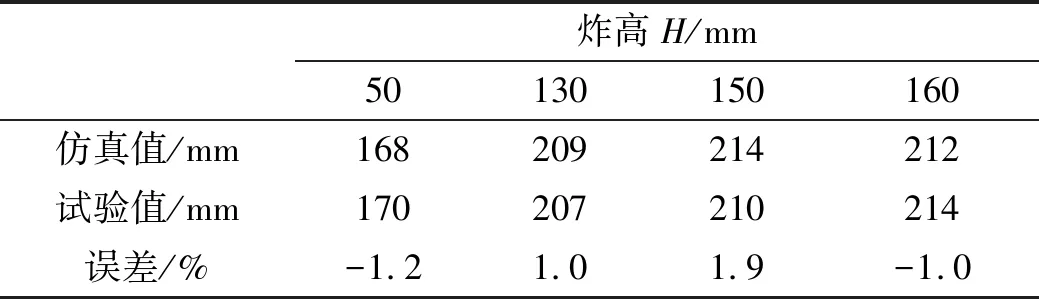
从图6和图7可看出:t=37 μs时射流到达靶板;37 μs 图6 炸高为150 mm时射流侵彻靶板过程 图7 炸高为150 mm时射流侵彻深度随时间变化曲线 为研究该聚能装药破甲深度的炸高不敏感性,炸高范围取50~300 mm进行射流侵彻靶板数值计算,不同炸高条件下射流最终侵彻深度如图8所示。表5列出了不同炸高条件下射流侵彻靶板孔径的具体参数,其中D为装药直径,h为侵彻深度,d为开孔直径。 根据图8侵彻深度对比可看出,炸高为50 mm时,靶板口部开孔直径较大,随侵彻深度的增加,孔径变化较小,孔内壁过渡平缓;炸高为100 mm时,靶板口部孔径有所减小,孔径变化较为明显,孔中部壁面较为平整;炸高为150~300 mm时,射流侵彻深度先有所减小,后开始增大,靶板孔径参数变化小;炸高继续增大至500 mm时,射流侵彻深度逐渐减小,且减小的幅度较为缓慢。 从表5中列出的数据发现,炸高为50~500 mm时,射流侵彻深度总体上呈先增大后减小的趋势,但是射流侵彻深度在增大和减小的过程中各存在一次波动。炸高为300 mm时,射流侵彻深度出现最大值为241 mm。炸高在0.78D~8.33D时,射流侵彻深度范围为168~241 mm。低炸高时射流开孔直径较大,随着炸高的增大,射流开孔直径基本上无变化。 图8 不同炸高下的射流侵彻数值计算结果 表5 不同炸高条件下射流侵彻靶板计算结果 在不改变装药高度和装药直径条件下,药型罩锥角分别取55°、60°和65°,药型罩厚度分别取1.1 mm、1.3 mm和1.5 mm。 为对比不同装药结构形成的射流到达靶板时参数,表6~表8分别列出了药型罩厚度为1.1 mm、1.3 mm和1.5 mm时不同药型罩锥角形成射流到达靶板时的射流长度L、头部速度vj和杵体速度vt。 从表6~表8中数据发现:同一药型罩厚度下,随着药型罩锥角的增大,射流到达靶板时的头部速度增大,杵体速度减小,射流头部和尾部速度差变大,因而射流长度变大。射流头部速度随炸高的增大而降低,且炸高在50~200 mm时,速度减小较快,炸高继续增大时,射流头部速度基本保持稳定状态。同样炸高在50~200 mm时,杵体速度增加较快,炸高继续增大时,杵体速度基本保持稳定状态。 根据图5中不同炸高下射流达到靶板时的形态发现,150 mm≤H≤250 mm时,射流拉伸长度已超过药型罩材料拉伸的极限长度,射流断裂成2段;炸高H=300 mm时,射流断裂成3段;继续增大炸高时,射流断裂越严重。因此炸高大于350 mm时形成的射流长度虽然较大,但侵彻能力可能会有所下降。 表9列出了不同药型罩锥角形成射流侵彻靶板仿真计算结果,图9(a)~图9(c)为药型罩厚度分别为1.1 mm、1.3 mm和1.5 mm时不同药型罩锥角形成射流的炸高曲线。 表6 药型罩厚1.1 mm下不同药型罩锥角形成射流到达靶板时参数 表7 药型罩厚1.3 mm下不同药型罩锥角形成射流到达靶板时参数 表8 药型罩厚1.5 mm下不同药型罩锥角形成射流到达靶板时参数 表9 不同药型罩锥角形成射流侵彻靶板计算结果 图9 不同药型罩锥角形成射流侵彻结果 由表9中仿真数据可看出:炸高为50~500 mm时射流破甲深度在最佳炸高之前和最佳炸高之后并不是单调递增和单调递减,破甲深度呈波动变化。药型罩厚度为1.1 mm和1.3 mm、药型罩锥角为55°~65°时,射流破甲深度极差先减小后变大;药型罩厚度为1.5 mm、药型罩锥角为55°~65°时,射流破甲深度极差逐渐变大。 从图9(a)和图9(b)中可看出:在药型罩厚1.1 mm和1.3 mm的情况下,当药型罩锥角为60°时,射流炸高曲线较为平缓,射流侵彻深度极差较小。药型罩厚度增大到1.5 mm后,药型罩锥角为55°形成的射流炸高曲线比药型罩锥角60°较为平缓,且极差小。 为降低炸高对射流破甲深度的影响,药型罩厚度一定且较小时,药型罩锥角取60°较好。药型罩厚度一定且较大时,药型罩的锥角应取小些。 表10列出了不同药型罩厚度形成射流侵彻靶板仿真计算结果,图10(a)~图10(c)分别为药型罩锥角55°、60°和65°时不同药型罩厚度形成射流的炸高曲线。 由表10中仿真数据可看出:药型罩锥角为55°、药型罩厚度为1.1~1.5 mm时,射流破甲深度极差逐渐减小;药型罩锥角为60°、药型罩厚度为1.1~1.5 mm时,射流破甲深度极差先变大后减小;药型罩锥角为65°、药型罩厚度为1.1~1.5 mm时,射流破甲深度极差逐渐变大。 表10 不同药型罩厚度形成射流侵彻靶板计算结果 从图10(a)和图10(b)中可看出,在药型罩锥角为55°、药型罩厚1.5 mm时,射流炸高曲线较为平缓,射流侵彻深度极差较小。药型罩锥角增大到60°后,3种药型罩厚度形成的射流侵彻深度极差相差不大,且在炸高为350 mm时,侵彻深度均有所降低。药型罩锥角继续增大到65°后,药型罩厚1.1 mm形成的射流侵彻深度曲线较为平缓,且极差较小。 为降低炸高对射流破甲深度的影响,药型罩锥角一定且较小时,药型罩厚度应取大些较好。药型罩锥角一定且较大时,药型罩厚度应取小些较好。 为了验证数值模拟方法的可信性以及炸高对射流侵彻45钢靶板的影响,进行了4种不同炸高射流侵彻试验,试验装置如图11所示。药型罩厚度为1.3 mm、锥角为60°,取炸高分别为50 mm、130 mm、150 mm和160 mm。靶板剖开后孔型及测量结果如图12所示,射流侵彻出现倾斜的原因是聚能装药安装在三脚架上时不稳,电雷管接线后,装药可能发生倾斜。表11列出了射流侵彻靶板深度试验与仿真对比。从图12和表11中数据对比发现,射流侵彻靶板深度的仿真结果与试验结果误差最大为1.9%,说明仿真模型、仿真参数和仿真结果都是可信的。 图10 不同药型罩厚度形成射流侵彻结果 图11 试验装置 表11 试验值和仿真值侵彻深度对比 炸高H/mm50130150160仿真值/mm168209214212试验值/mm170207210214误差/%-1.21.01.9-1.0 图12 静破甲试验靶板剖面孔型图 对不同炸高条件下聚能装药结构射流破甲性能进行了数值仿真研究,并通过试验验证进行了对比分析,得出以下结论: 1)通过AUTODYN软件仿真计算得到在炸高为50 mm、130 mm、150 mm和160 mm时射流破甲深度分别为168 mm、209 mm、214 mm和212 mm,试验破甲深度分别为170 mm、207 mm、210 mm和214 mm,仿真结果与试验结果误差最大为1.9%,说明仿真方法和效果是可信的。 2)在药型罩厚1.1 mm和1.3 mm下,药型罩锥角为60°时,射流炸高曲线较为平缓,射流侵彻深度极差较小。药型罩厚度增大到1.5 mm后,药型罩锥角为55°形成的射流炸高曲线比药型罩锥角60°较为平缓,且极差小。为降低炸高对射流破甲深度的影响,药型罩厚度一定且较小时,药型罩锥角取60°较好。药型罩厚度一定且较大时,药型罩的锥角应取小些。 3)在药型罩锥角为55°,药型罩厚1.5 mm时,射流炸高曲线较为平缓,射流侵彻深度极差较小。药型罩锥角增大到60°后,3种药型罩厚度形成的射流侵彻深度极差相差不大。药型罩锥角继续增大到65°后,药型罩厚1.1 mm形成的射流侵彻深度曲线较为平缓,且极值较小。为降低炸高对射流破甲深度的影响,药型罩锥角一定且较小时,药型罩厚度取大些较好。药型罩锥角一定且较大时,药型罩厚度取小些较好。 4)在不考虑聚能装药最大破甲威力的前提下,凡是能缩短射流断裂时间并减小射流与杵体速度差的设计方案都有利于提高聚能装药破甲深度的炸高不敏感性。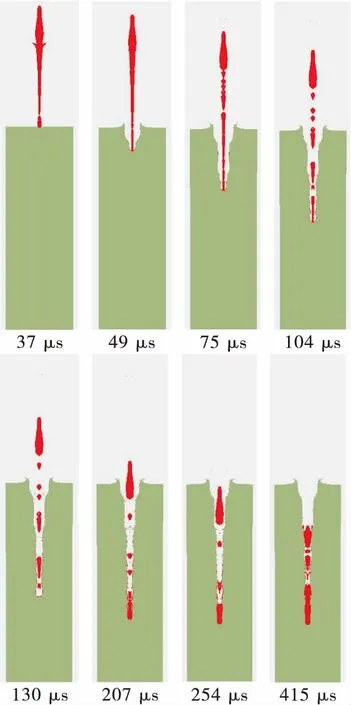

2.3 不同炸高射流侵彻45钢靶板结果对比

3 药型罩参数对聚能装药破甲深度炸高不敏感性的影响
3.1 锥角对聚能装药破甲深度炸高不敏感性的影响


3.2 厚度对聚能装药破甲深度炸高不敏感性的影响
3.3 试验对比分析


4 结论

