思维可“视”，分析有“道”

徐兰

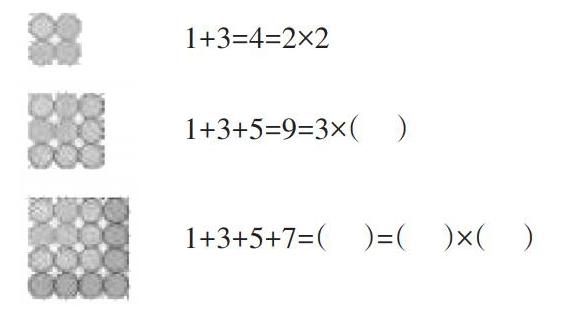
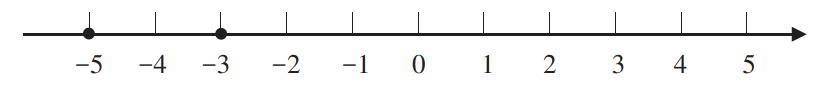
[摘要]现行的苏教版小学数学课本在编排时将“解决问题的策略”单独设置为一个模块，引入了很多的解题策略，而画图就是最常用的解题策略之一。在课堂教学中，教师应引导学生借助画图有序推理并抽象思维，深化对所学知识的理解，构建富有生命力的数学课堂。

[关键词]小学数学;画图策略;思维

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）14-0086-02

众所周知，“数”与“形”是数学的基本元素，两者相辅相成，缺一不可。数学家华罗庚说过：“数无形，少直观;形无数，难人微。”这一精辟的论述充分说明数形结合的重要性。处在小学阶段的学生由于缺少生活经验且思维能力薄弱，在学习过程中难以把握知识的内涵，也无法在大脑中建构起数学模型，影响了知识体系的建构。因此，在小学数学课堂教学中，教师应充分挖掘教材，培养学生的画图意识，让画图成为学生的一种思维方式，让复杂的数学问题简单化、形象化、直观化，使学生对知识的认知由模糊走向清晰，使画图策略真正成为学生享用一生的宝贵财富。

一、以图促辨，明晰概念内涵

数学概念抽象，学生理解起来有一定的难度，无法准确把握概念的内涵和外延。而画图策略可以将抽象的概念直观化、简单化、形象化，帮助学生把握数学概念的本质属性，建构良好的知识结构。尤其是教学容易混淆的数学概念时，教师可以引导学生画出集合图，增强对概念的理解。

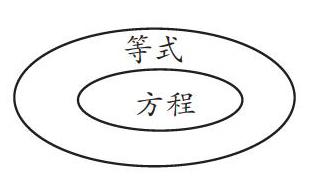
在教学等式和方程内容时，教师在天平的左边放了一个50克的鸡蛋和一个50克的砝码，在天平的右边放了一个100克的砝码，这时天平平衡了。学生想到了“50+50=100”。教师顺势揭示出等式的概念：“含有等号的式子叫作等式，如60+100=160，70+80=150，200-100=100等都是等式。”然后，教师将50克的砝码换成了x克的砝码，这时天平又平衡了。学生想到了“x+50=100”。教师趁势揭示方程的概念：“含有未知数的等式叫作方程。”教学如果就此结束，学生对等式和方程势必难以正确地进行区分，所以教师可以画出集合图。学生通过观察图形，就能理解“所有的方程都是等式，但等式不一定是方程”这句话的含义。

上述案例中，教师在教学时适时地引入画图策略，不仅让学生辨析出等式和方程的异同，还培养了学生的集合思想，取得了较为理想的教学效果。

二、以图介入。找出内在规律

随着课改的不断推进，现行不同版本的小学数学课本对“探索规律”的内容都进行了合理的选择和精心设计。这部分教学内容对学生的抽象逻辑思维要求较高。因此，在课堂教学的过程中，教师应合理设計探索规律的题目，在学生难以找到突破口时将图形引入其中，让学生经历探索规律、发现规律、运用规律的全过程。

在教学奇数内容时，教师出示题目：1+3，1+3+5，1+3+5+7，…，1+3+5+7+9+11+13+15，让学生在1分钟之内完成。学生面面相觑，认为这怎么可能？教师没有急于点破，而是让学生画圆，看看有什么发现。

学生通过画圆发现了规律：连续。个奇数相加的和等于。的平方。教师继续引导学生举了一些例子进行验证，发现这个规律准确无误，说明其具有广泛性。

上述案例中，在探索规律的过程中教师引导学生画图，帮助学生发现了规律，强化学生对所学知识的印象，积累了探索规律的经验，从而赋予数学课堂更加深刻的意义。

三、以图架桥，培养良好数感

数轴是学生研究数学的有效工具，它可以帮助学生更深入地认识数，理解数与数之间的关系，更好地帮助学生建立数感。数轴上的点与数有明确的对应关系，借助数轴不仅可以帮助学生感受到数的排列是有规律、有方向的，还可以帮助他们比较数的大小，区分正数和负数，揭示数的本质，培养良好的数感。因此，在数学课堂教学过程中，应引导学生灵活地运用数轴，使抽象的数变得有形可依。

在教学“负数的认识”时，学生在比较-5和-3时，认为-5>-3，很显然，学生受正数的影响，有了思维定式。面对这种情况，教师没有直接说出答案，而是请学生在数轴上描点，然后标出-5和-3。

学生发现数轴上的各点都是按照一定顺序排列的：如果从左向右看，就是从小到大的顺序;从右往左看，就是从大到小的顺序。在数轴上，“-5”在“-3”的左边，所以-5<-3。

上述案例中，在学生有困惑时，教师请来数轴帮忙，通过数形结合，让学生学会比较负数的方法，从而建立起数感。

四、以图为媒，探索解题策略

学生在学习数学的过程中，经常会被信息量大、数量关系复杂的信息所干扰，难以找到有效的解题思路。而以画图为媒介，对问题展开分析，可使抽象的问题直观化，复杂的数量关系明晰化，深奥的算理有序化，有效的解题方法明朗化。因此，在数学课堂教学中，当学生遇到难题时，教师应把数转化成形，帮助学生寻找解决问题的突破口。

在教学“解决问题”时，教师出示了这样的问题：街心花园有一个长方形花圃，它的长是8米，后来对其进行扩建，花圃的长增加了3米，花圃的面积增加了18平方米，这个花圃原来的面积是多少平方米？出示题目后，学生发现这道题无法直接运用长方形的面积计算公式进行解答。有的学生想到了画图。教师肯定了学生使用画图的想法，并指导学生将“长增加3米”画了出来。

教师问：“观察图形，你发现什么变了？什么没有变？”学生发现花圃的长增加了，面积增加了，宽没有变化。教师追问：“比较花圃增加的部分和原来的花圃，它们有什么联系？”学生说：“花圃增加部分的宽是原来花圃的宽。”基于这样的思考，学生很快就列出了算式，顺利地解决了问题。

上述案例中，在学生一筹莫展之时，教师没有直接讲解，而是让学生画图，以图形为媒介，变“看不见”的知识为“看得见”的知识，扩大了学生思维的边界，提升了学生的画图意识和解题能力。

总之，在数学的教学过程中，画图是促进学生思考的一种手段，能高效地帮助学生解决数学问题。因此，在以后的数学课堂中，教师应将画图策略贯穿课堂教学的始终，培养学生的画图技能，最终让学生领略画图策略独特的价值和魅力！

（责编：黄露）