非正规子群彼此同构的有限群

石化国 韩章家 张隆辉

(1.四川职业技术学院 教师教育系,遂宁,629000；2.成都信息工程大学 应用数学学院,成都,610225)

1 引言

本文所讨论的群均为有限群, 除非特别说明, 本文所使用的符号都是标准的(见[8]).

所有子群皆正规的群称为 Dedekind 群.Dedekind 群在讨论有限群的结构中扮演很重要的角色, 自 R.Dedekind, E.Wendt 和R.Bare给出Dedekind 群的结构后(见[5]), 许多群论工作者从不同的角度对 Dedekind 群进行了推广, 得到了大量的成果, 在此不一一赘述, 仅举几例来说明.比如, 石化国、韩章家和陈贵云教授[6]以及R.Brand[2]讨论了非正规子群彼此共轭的有限群的结构; 陈顺民和陈贵云教授[3-4]讨论了非正规子群共轭类数为2和3的有限群的性质和结构.

其实我们可以换个角度来看待以上这些研究.显然Dedekind群既可以看作是非正规子群个数为零的群，也可以看作是非正规子群共轭类个数为零的群, 所以以上提及的文献从非正规子群共轭类数这个角度对 Dedekind 群进行推广就比较自然了.

进一步地, 探讨具有特定群论性质的非正规子群对有限群结构的影响也是一件很有意思的工作, 例如 A.Fattahi在[1]中给出了非正规子群皆反正规(abnormal)的有限群的结构; 张勤海教授[9]给出了非正规子群皆自正规的有限群的结构; 石化国、韩章家、江磊[2]讨论了非正规子群均为素数阶的有限群的结构等.这些研究都是从非正规子群具有某一特性的角度对 Dedekind 群进行推广.本文将继续这一思路讨论非正规子群彼此同构的有限群, 并最终确定其结构.

我们的主要结论是:

主要定理设G为有限群,G的非正规子群彼此同构当且仅当G同构于下列群之一:

(1)非正规子群彼此共轭的有限群;

(2)非正规子群的阶均为素数的有限p-群;

(3)16阶广义四元数群Q16;

(4)四元数群Q8与4阶循环群的直积;

(5)亚循环群G=.

2 预备知识

为了完成主要定理的证明, 我们首先给出如下的一些结论.

引理2.1([6], Main Theorem) 设G为有限群,G的非正规子群彼此共轭当且仅当G同构于下列群之一:

(1)G=;

(2)G=;

(3)G=.

引理2.2([2], Main Theorem) 有限群G的的非正规子群的阶均为素数当且仅当G同构于下列群之一:

(1)非正规子群彼此共轭的有限群;

(2)G=;

(3)G=;

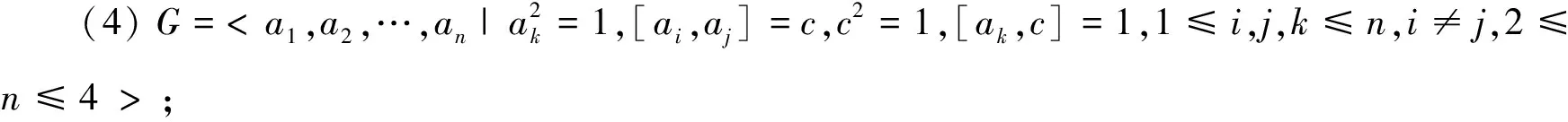
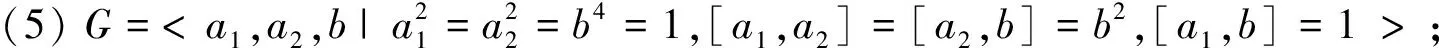
(6)G=.

引理2.3设有限群G的非正规子群阶不为素数, 若G的非正规子群彼此同构,则G为一个p-群.

证明断言G为幂零群.否则存在G的一个Sylow 子群非正规,于是由G的非正规子群彼此同构,便有G的非正规子群彼此共轭.再由([6]Main Theorem)就可得G的非正规子群的阶为素数, 矛盾.断言得证.

设H为G的非正规子群,则至少存在H的一个Sylowp-子群P非正规于G, 由于G的非正规子群彼此同构, 因此有H=P.又G幂零,故G的Sylowp-子群P1正规于G且PP1.若G不是p-群, 则存在G的Sylowq-子群Q正规于G.同样地, 由于G的非正规子群彼此同构,故PQG, 这样有P=P1∩PQG, 矛盾.所以G为p-群,引理得证.

引理2.4设G为有限2-群, |Ω1(G)|≠2, 且G的非正规子群的阶不为素数.若G的非正规子群彼此同构, 则G/Ω1(G)中不包含四元数群.

证明用反证法.假设G/Ω(G)中存在一个四元数子群KΩ1(G)/Ω1(G).由于G的非正规子群的阶不为素数且彼此同构, 故Ω1(G)为初等交换2-群, 于是K∩Ω1(G)=Ω1(K).记Ω=Ω1(K), 则KΩ1(G)/Ω1(G)≅K/K∩Ω1(G)=K/Ω为四元数群.

任取K/Ω的一个最小生成系{aΩ,bΩ}, 则有a4Ω=Ω,b2Ω=a2Ω, 且[a,b]Ω=a2Ω.因Ω是初等交换2-群且包含于Z(K), 故a,b均为8阶元,a2,b2,[a,b]均属于Z(K)且[a,b]2=a4, 于是有1=[a,b2]=[a,b]2=a4, 矛盾.引理得证.

下面的引理在本文中是不可或缺的.

引理2.5设p为素数,G为有限p-群, Ω1(G)不为循环群, 并且G的非正规子群的阶不为素数.若G的非正规子群彼此同构,则有：

(1)G′≤Ω1(G);

(2)G的Frattini 子群Φ(G)≤Z(G);

(3)Ω1(G)为(p,p)型交换群且含于Φ(G).

证明由于G的非正规子群不是素数阶群且彼此同构,所以Ω1(G)为初等交换群且包含于Z(G).又Ω1(G)不为循环群,于是对G的任意元a都有aΩ1(G)G, 故G/Ω1(G)为Dedekind 群.再由引理2.4,G/Ω1(G)为交换群, 故对G的任意两个元a,b都为[a,b]∈Ω1(G)且为p阶元, 于是有G的换位子群G′≤Ω1(G).因[a,b]为p阶元,故[ap,b]=[a,b]p=1.再由a,b的任意性知ap∈Z(G), 固有Φ(G)≤Z(G).

若Ω1(G)不是(p,p)型交换群,则存在Ω1(G)的三个不同的素数阶子真群A1,A2,A3, 使得A1A2A3=A1×A2×A3.这样对G的任意循环子群A有A=AA1∩AA2∩AA3◁G,矛盾于G中有非正规子群, 于是Ω1(G)为(p,p)型交换群.

若Ω1(G)Φ(G), 则存在G的子群H和p阶子群B, 使得G=H×B.因Ω1(G)为(p,p)型初等交换群, 故H为循环群、四元数群或广义四元数群.当H为循环群或四元数群时,G为Dedekind-群.当H为广义四元数群时, 可以验证G的非正规子群不彼此同构, 都不可能.引理得证.

3 主要结论的证明

定理3.1设p为素数,G为有限p-群.如果G的非正规子群的阶不为素数, 并且G中包含四元数群, 则G的非正规子群彼此同构当且仅当G为16 阶广义四元数群Q16, 或G为四元数群Q8与一个4阶循环群的直积.

证明我们分两种情况来证明.

(1)G中含有16阶广义四元数群Q16.

设H=为G的16阶广义四元数子群.显然不正规于G.若|Ω1(G)|≠2, 取w∉H为G的一个2阶元, 由G的非正规子群彼此同构有◁G,H◁G, 于是=∩H◁G, 矛盾.故|Ω1(G)|=2,G为广义四元数群.若|G|≥32, 则不正规于G, 矛盾于G的非正规子群彼此同构, 故此时G应为16 阶广义四元数群Q16.显然，此时G的非正规子群彼此同构.

(2)G中不含16阶广义四元数群Q16.

令H=为G的四元数子群, 显然此时Ω1(G)不是循环群, 故H的每一个循环子群均正规于G.

断言G的方次数为4.否则取G中的8 阶元a.若a2∈H, 由引理2.5知H为交换群, 矛盾于H是四元数群.若a4∈H, 则ua2,va2为G的两个不同的2阶元, 而(ua2va2)2≠1, 矛盾于引理2.5.这样∩H=1, 于是G的4 阶子群非正规于G, 从而G的8阶子群是正规的.这样我们就有[u,a]=[v,a]=1, 进一步有8 阶子群也非正规于G, 矛盾于G的非正规子群彼此同构.断言得证.

设A=为G的一个非正规的4阶循环子群, 显然a2∉H, 否则A=∩◁G, 矛盾.又H的每个子群均正规于G, 故可选取适当的4阶循环子群B=, 使得=H×B.此时, ◁G,H×B的非正规子群彼此同构，且由引理2.5有Ω1(G)=Ω1(H×B)=Φ(G)=Φ(H×B)≤Z(G).

断言G=H×B.若断言不成立，则存在G的4 阶元c, 使得cH×K.显然c2≠u2(否则，由H的每个子群皆正规于G知存在H的一个4阶元，不妨仍设为u, 使得cu=uc, 于是(cu)2=1且=, 矛盾).这样存在4阶子群D=使得=H×D.显然d2=b2或b2u2.

当d2=b2时, 有(bd)2=b2d2[d,b]=[d,b].若[d,b]=1, 则bd∈Ω1(G)=Φ(H×B)且=, 矛盾.若[d,b]=u2, 则(bdu)2=1且=, 矛盾.若[d,b]=b2, 则为四元数群，进一步有◁G, 矛盾.若[d,b]=b2u2, 则(bd)2=(bu)2, 又[bu,bd]=(bd)2, 于是为四元数群, ◁G, 同样矛盾.

当d2=b2u2时,(dbu)2=d2(bu)2[bu,d]=[bu,d], 若[d,bu]=1, 则bud∈Ω1(G)=Φ(H×B)且=, 矛盾; 若[d,bu]=u2, 则(db)2=1且=, 矛盾; 若[d,bu]=b2u2, 则为四元数群，进一步有◁G, 矛盾; 若[d,bu]=b2, 则[du,b]=[d,b]=[d,bu]=b2, 又由d2=b2u2有(du)2=b2, 于是为四元数群, ◁G, 但(du)v∉, 矛盾, 断言得证.容易验证, 此时G的非正规子群彼此同构.定理证毕.

定理3.2设p为素数,G为有限p-群.如果G的非正规子群的阶不为素数, 并且G中不含四元数群, 则G的非正规子群彼此同构当且仅当G=.

证明因G不含四元数群, 由引理2.5有G′≤Ω1(G)≤Z(G)且Ω1(G)为(p,p)型交换群.下面分三步完成定理的证明.

(1)G为二元生成群,G′为p阶循环群.

用反证法.若G不为二元生成群, 在G的一个最小生成系中取3个元u,v,w, 由引理2.5知up≠1,vp≠1均包含于Z(G).于是为交换群, 不妨记为H.再由引理2.5, Ω1(G)为(p,p)型交换群, 故H为循环群或两个循环群的直积.若为前者, 则有up∈w, 此时中存在循环极大子群, 又G中不存在四元数群, 于是存在一个p阶元u1∈使得=.由引理2.5, Ω1(G)≤Φ(G), 故有u∈, 这将矛盾于u,v,w是G的最小生成系中的3个生成元.若为后者, 则H为二元生成群, 于是在up,vp,w三个元中能选出两个元生成H.若是=H, 则w∈, 这将与H为循环群的情形一样可导出矛盾.如果=H, 也类似于H为循环群的情形可导出矛盾.同理也可以证明≠H.这样,G为二元生成群,G′为p阶循环群.结论得证.

(2)G为亚循环群.

显然存在G的一个生成系{u,v}使得◁G.若不正规于G, 结论已经得证, 故设不正规于G.由于G的非正规子群彼此同构, 故u的阶等于v的阶(设为pm)且[u,v]不属于, 也不属于.

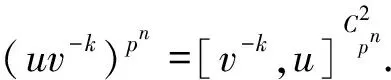
若u∩v=1,则存在k,t, 使得p⫮k,p⫮t且G′=.又(ukvt)pm-1=ukpm-1vtpm-1[vt,uk]∈G′.若(ukvt)pm-1=1, 则ukvt的阶小于pm.进一步◁G, 这样G=为亚循环群.若(ukvt)pm-1≠1, 则G′≤, 这样◁G,G=也为亚循环群.结论得证.

(3)完成证明.

选取G的适当的生成元a,b使得不正规于G且apm=1,bpn=apt,[b,a]=apm-1.断言t=m, 即apt=1.否则t≤m-1, 由[b,a]=apm-1有ba=bapm-1∈, 这样◁G, 矛盾.故G=.可以验证, 此时G的非正规子群彼此同构, 定理得证.

下面我们来证明本文的主要结论.

主要定理的证明显然当G的非正规子群彼此共轭时G的非正规子群彼此同构, 即G为类型(1)中的群.

当G为非正规子群的阶均为素数的有限p-群时,G的非正规子是彼此同构的.当G为非正规子群均为素数的非p-群时, 根据引理2.2, 当且仅当G的非正规子群彼此共轭时,G的非正规子群彼此同构.所以当G的非正规子群的阶为素数时, 当且仅当G为类型(1)或类(2)中的群之一时G的非正规子群彼此同构.下设G的非正规子群的阶不为素数.由引理2.3 知, 此时G为一个有限p-群.当G中含有四元数群时, 由定理3.1知,G的非正规子群彼此同构当且仅当G为类型(3)或类型(4)中的群之一, 当G不含四元数群, 由定理3.2知G的非正规子群彼此同构当且仅当G为类型(5)中的群.定理证毕.