两类具有2-等变性的Liénard系统的全局动力学
陈和柏 阳豪 张瑞
(中南大学 数学与统计学院,长沙,410083)
1 背景介绍和主要结果
在1900年,著名数学家Hilbert在世界数学家大会上提出了著名的Hilbert 23个问题[16].直到现在,这些问题还在引领世界数学发展,其中还有多个无法解决.关于Hilbert第16问题的第二部分,讲述的是
(1.1)
的最大极限环数,以及它们的相对位置,其中P,Q是次数不高于n次的多项式.当n=1时, 系统(1.1)无极限环.然而,即使是n=2的情形,我们也仅知道其最大极限环数大于等于4.著名数学家Smale在[25]中写到“I spent much time on the following special case of problem 7, corresponding to Liénard’s equation”,即花费许多时间来解决该猜想,但也毫无头绪, 并在[25, 26]中建议先解决限制在Liénard系统上的Hilbert第16问题.Lins,Melo和Pugh在[20]中研究了如下的Liénard系统
(1.2)

和
其中F(x)是关于x的五次多项式,ε是充分小的正数,对Lins-Melo-Pugh猜想给出了肯定回答.进一步可以问,对n≥6的情形,系统(1.2)的最大极限环是关于n的一个什么函数关系.关于该猜想的更详细的结果和发展,可参见[19].
上面讲述的均是g(x)=x的结果,还有更多关于多项式Liénard系统的结果,可参见[4, 5, 23].现在介绍g(x)为二次及更高次多项式的结果.当g(x)为二次多项式且f(x)为一次多项式时,1988年Coppel[8]给出了其极限环的唯一性;1992年Perko[24]给出了其完整的分岔图和全局相图;2013年Gasull等[14]发展了[15]中的方法给出了Perko对其同宿分岔曲线性质的猜想.当g(x)为三次多项式且f(x)为一次多项式时,1990年Dumortier和Rousseau[13]给出了完整的分岔图和全局相图(除了焦点情形中围绕三个奇点的极限环的唯一性是猜测外);1996年Dumortier和李承治[11]发展了Coppel方法证明围绕三个奇点的极限环的唯一性问题,即解决了Dumortier本人和Rousseau的猜想.当g(x)为二次多项式且f(x)为二次多项式时,1997年Dumortier和李承治[12]完整地给出了其分岔图和全局相图.到目前为止,只有这几类多项式Liénard系统被完整研究,而且它们的极限环数目至多为1.

(1.3)
其中(a,b,c)∈2×[0,+∞),其有限远奇点以及极限环的个数问题已经在[6]中给出,但是该系统在Poincaré圆盘上的全局相图还没有完整给出.在本文中,我们进一步给出完整的分岔图以及在Poincaré圆盘上的全局相图.
定理1.1系统(1.3)的分岔图由以下分岔曲面构成
(a)超临界Hopf分岔曲面:H1={(a,b,c)∈2×[0,+∞)|a=0,b>0};
(b)次临界Hopf分岔曲面:H2={(a,b,c)∈2×[0,+∞)|a=0,b<0};
(c)二重环分岔曲面:DL={(a,b,c)∈2×[0,+∞)|b=η(a,c)};
(d)Bautin分岔曲线:O={(a,b,c)∈2×[0,+∞)|a=b=0},

并且η(a,c)是a的减函数.分岔曲面在c=c0≥0时的切面以及在Poincaré圆盘上的全局相图如图1所示,其中

图1 系统(1.3)的分岔图的切片c=c0≥0和在Poincaré圆盘上的全局相图
I={(a,b,c)∈2×[0,+∞)|a>0,b>η(a)},
II={(a,b,c)∈2×[0,+∞)|a>0,b<η(a)},
III={(a,b,c)∈2×[0,+∞)|a<0}.
(1.4)
其中(a,b,c)∈2×+,我们有如下的定理.
定理1.2系统(1.4)的分岔图由下列分岔曲面构成
(a)广义超临界Hopf分岔曲面∶H1={(a,b,c)∈2×+|a=0,b≥0};
(b)广义次临界Hopf分岔曲面∶H2={(a,b,c)∈2×+|a=0,b<0};


图2 系统(1.4)的分岔图的切片c=c0≥0和在Poincaré圆盘上的全局相图
I={(a,b,c)∈2×+|a>0,b>φ(a)},
II={(a,b,c)∈2×+|a>0,b<φ(a)},
III={(a,b,c)∈2×+|a<0}.
本文第二部分回顾一些关于Liénard系统唯二性的结果以及多项式Liénard系统(1.3)和(1.4)在Poincaré圆盘上无穷远处的轨道性质,第三部分给出主要定理结果证明,第四部分给出数值结果.
2 预备知识
为了证明主要结果,在本节中,我们引入一些已有的结果.考虑如下的广义Liénard系统
(2.1)

定理2.1[6, Theorem 1.1] 针对系统(2.1),假设下列条件成立:
(C1)F(x)在某区间(-d,d)内Lipschitz连续,且F(-x)=-F(x);
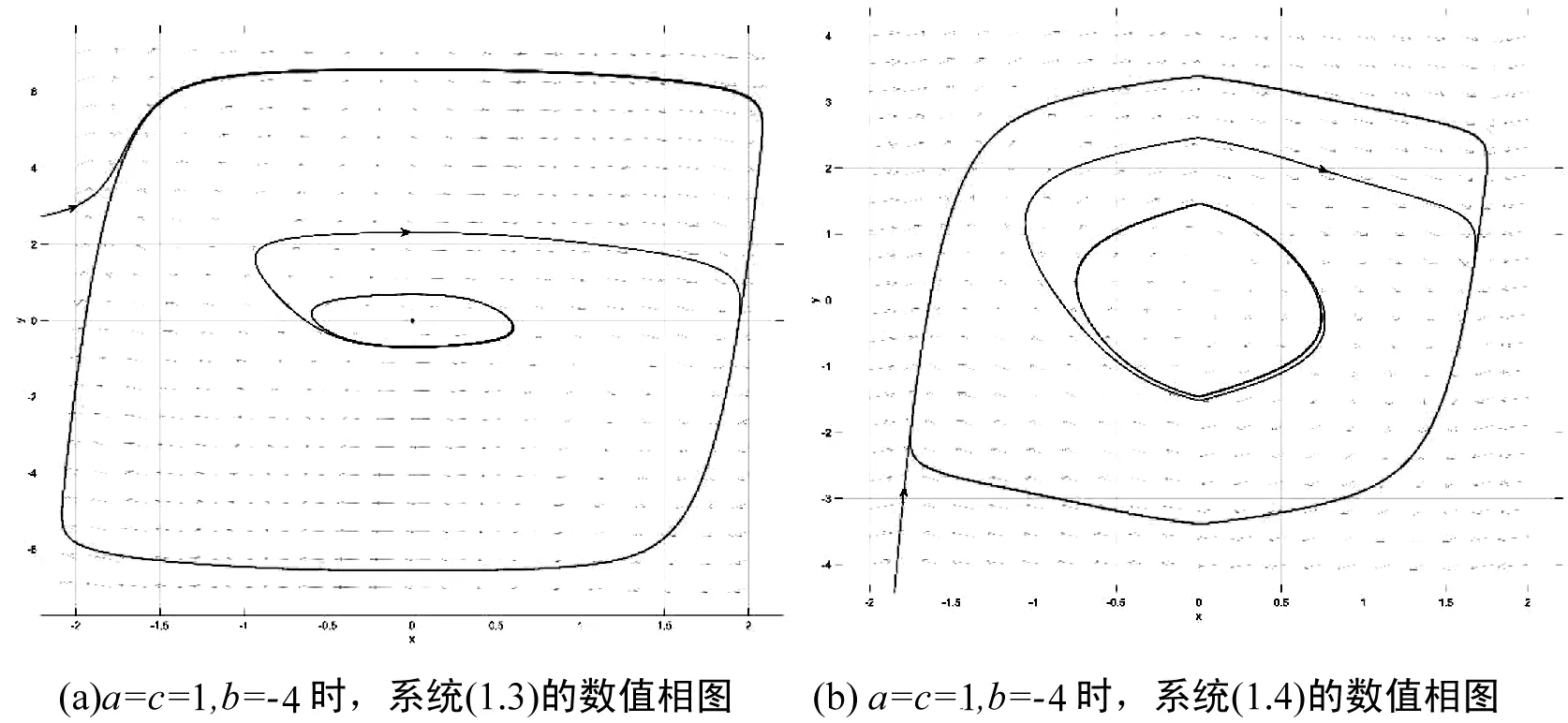
(C2)当x=β1,β2时,F(x)=0;当x∈(β1,β2)时,F(x)<0;当x∈(0,β1)∪(β2,d)时,F(x)>0,且当x∈(β1,α1)∪(α1,d)时,F(x)∈C1,当x∈(β1,α1)时,F′(x)≤0,其中0<β1<α1<β2 (C3)g(x)∶=g0(x)+csgn(x),其中c≥0,g0在(-d,d)内Lipschitz连续且对任意x≠0,xg0(x)>0; 2.5.3 包封率和载药量 精密量取白藜芦醇DPPC脂质体粉雾剂10 mg,纯化水复溶,加入预先溶胀的葡聚糖凝胶G-25色谱柱中分离,顶部加纯化水洗脱,收集洗脱液,每管2 mL,分别加入无水乙醇定容至10 mL,参考“2.1.2”项色谱条件测定。计算包封率、载药量。 (C4)f(x)或者(F(x)-F(α1))f(x)g(x)在x∈(α1,d)上单调不减. 则系统(2.1)至多有两个极限环,且当极限环存在时,或者有一个稳定极限环和一个不稳定极限环,或者仅有一个半稳定极限环. 定理2.3[10] 考虑多项式Liénard系统 (2.2) 其中m 图3 系统(2.2)在m为奇数,n为偶数,ε=1时的无穷远处的性质 3.1 定理1.1的证明 我们只需确定系统(1.3)在无穷远处的轨线性态即可.为此,对系统(1.3)做如下变换 x′=51/3x,y′=52/3(y-51/3bx3-5x5),t′=5-1/3t. 为了叙述方便,仍用(x,y,t)代替(x′,y′,t′).此时系统(1.3)可改写成 (3.1) 系统(3.1)满足定理2.3的条件,它与系统(2.2)在无穷远处的轨道性质是拓扑等价的.实际上,系统(3.1)在x轴上的无穷远奇点为结点,在y轴上的无穷远奇点为鞍点.由于在区域I∪H1内,系统(3.1)没有极限环,唯一奇点是稳定的,无穷远处轨线是发散的,故连接无穷远处的所有轨线的ω极限集为唯一奇点O,因此连接无穷远处的所有轨线也连接O;在区域II内,系统(3.1)有唯一奇点O,O是稳定的,且有一个不稳定极限环Γ1和一个稳定极限环Γ2,Γ2环绕Γ1,因此连接无穷远点的所有轨线的ω极限集为Γ2;在区域III∪H2内,系统(3.1)有唯一稳定的极限环,显然连接无穷远点的所有轨线的ω极限集为此唯一极限环;在DL上,系统(3.1)有一半稳定的极限环,同样地,连接无穷远点的所有轨线的ω极限集是这一半稳定极限环.由于系统(3.1)无穷远奇点无分岔发生,分岔图直接可由[6]直接得到,定理得证. 3.2 定理1.2的证明 为了证明定理1.2,首先给出如下几个引理. 引理3.1当a>0或者a=0且b≥0时,系统(1.4)的原点O是一个汇;当a<0或者a=0且b<0时,O是一个源.系统(1.4)在无穷远处的轨线性质如图3所示. 证明显然 Σ={(x,y)∈2|x=0} 是系统(1.4)的不连续线.此外,Σ将x-y平面划分成了3个子区域Σ-,Σ,Σ+,其中 Σ-={(x,y)∈2|x<0}, Σ+={(x,y)∈2|x>0}. 因此系统(1.4)可以改写成 (3.2) 运用Filippov方法[1, 18],考虑在区域Σ-和Σ+上的标准解以及不连续线Σ上的滑移解.记 σ(x,y)=<(Hx,Hy),(y-F(x),-x+c)>|x→0-·<(Hx,Hy),(y-F(x),-x-c)>|x→0+, 这里<·,·>代表内积,H(x,y)=x.显然有σ(x,y)=y2,且穿越集Σc和滑移集Σs分别为 Σc={(x,y)2|x=0,y≠0}, Σs={(x,y)2|x=0,y=0}. 同时,在(0,0)处,内积 <(Hx,Hy),(y-F(x),-x+c)-(y-F(x),-x-c)>=0, 也就是说(0,0)是系统(1.4)的奇异滑点. 由于O∈Σ,则在O处的Jacobi矩阵不存在.设 (3.2) 则很清楚地得到 (3.3) 当|x|充分小时,dE/dt的符号完全由a,b的符号决定,即 现在,我们有以下断言:系统(1.4)的从点(0,y0)出发的流φ(t;0,(0,y0))(这里y0>0且充分小)经过有限时间t0会再次回到y轴正半轴,即φ(t0;0,(0,y0))=(0,y1)(这里y1>0且充分小),或者直接连接O. 事实上,考虑Hamilton系统 (3.4) 设系统(3.4)过(0,y0)的解为ψ(t).显然ψ(t)为闭轨,周期为T.根据解对参数的连续依赖性,断言显然成立.此外,关于y1与y0的大小关系,我们有 因此,当a>0或者a=0且b≥0时,y1 假设系统(1.4)过初始点(0,y0)(y0>0)的轨线为φ(t;0,(0,y0)),经过时间t0,轨线返回y轴正半轴且交于点(0,y1),则 即轨线朝着靠近O(0,0)的方向偏移,因此系统(1.4)在此参数条件下不存在闭轨线. 引理3.3若a<0,b∈或者a=0,b<0,则系统(1.4)有唯一的极限环,且是稳定的. 证明先证极限环的存在性.由引理3.1可知,原点在此参数情况下是不稳定的.由无穷远奇点是发散的和Poincare-Bendixson环域定理可知,此时系统(1.4)必存在稳定极限环.我们记最靠近原点O的极限环为Γ1. 再考虑唯一性.当a<0,b∈或者a=0,b<0时,F(x)=ax+bx3+x5仅有一个正实根当x∈(0,β2)时,由引理3.1可知 因此极限环Γ1不可能位于带状区域|x|≤β2的内部,从而它一定会环绕包围(-β2,0),(β2,0). 假设除Γ1以外,系统(1.4)还存在其它极限环Γ2,则必有Γ2环绕Γ1.如图4所示,其中A1,D1是Γ1与x=-β2的交点,A2,D2是Γ2与x=-β2的交点,B1,C1是Γ1与x=β2的交点,B2,C2是Γ2与x=β2的交点,E2,F2,G2,H2分别是与A1,B1,C1,D1有着相同纵坐标且位于Γ2上的点. 图4 当a<0,b∈或者a=0,b<0时,系统(1.4)的极限环 显然 从而 因此 (3.4) 同理可得 (3.5) 令yB1=yF2=y1,yC1=yG2=y2,则当y1≥y≥y2时,x2(y)>x1(y).由F(x)的性质,在x∈(-∞,-β2)∪(β2,∞),F(x)是单调递增的,故F(x1(y)) 即 (3.6) 同理可得 (3.7) 又因为x>|β2|时,g(x)F(x)>0, 故我们有 (3.8) 由式(3.4)-(3.8)可得 证明此时,F(x)=ax+bx3+x5,g0(x)=x,定理2.1中条件(C1)和条件(C3)成立.在这种条件下,F(x)存在两个正实根β1,β2,其中 同时,f(x)=F′(x)=a+3bx2+5x4也存在两个正实根 另一方面,当x≥α1=x2时, (a)系统(1.4)恰有一个极限环且是半稳定的当且仅当b=φ(a,c); (b)系统(1.4)有两个极限环且外环是稳定的,内环是不稳定的当且仅当b<φ(a,c); (c)系统(1.4)没有极限环当且仅当b>φ(a,c). 结合上述引理,定理1.2得证. 当(a,b,c)=(1,-4,1)∈II时,由定理1.1和1.2,系统(1.3)和(1.4)皆有两个极限环.通过数值仿真,系统(1.3)和(1.4)的确恰有两个极限环,如图5所示.这验证了我们的理论结果.此外,在相同的参数条件下,我们发现光滑系统(1.3)稳定极限环的振幅大于非光滑系统(1.4)稳定极限环的振幅,光滑系统(1.3)不稳定极限环的振幅确小于非光滑系统(1.4)不稳定极限环的振幅. 图5 系统(1.3)和系统(1.4)在II上的数值相图 当a=c=1,b≈-2.0868时,通过数值仿真,系统(1.3)恰有一个半稳定极限环;当a=c=1,b≈-2.144545时,通过数值仿真,系统(1.4)恰有一个半稳定极限环.由此可知,系统(1.3)和(1.4)的半稳定分岔曲面的函数表达式不一样,这也说明了分岔图是不一样的. 通过数值仿真,我们可以进一步得到φ(a,c)<η(a,c),即系统(1.4)的二重环分岔曲面位于系统(1.3)的二重环分岔曲面的下方. 图6 系统(1.3)和系统(1.4)在各自半稳定分岔曲面上的数值相图
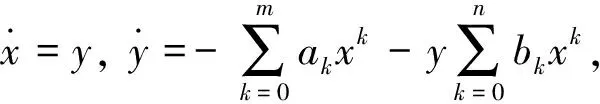
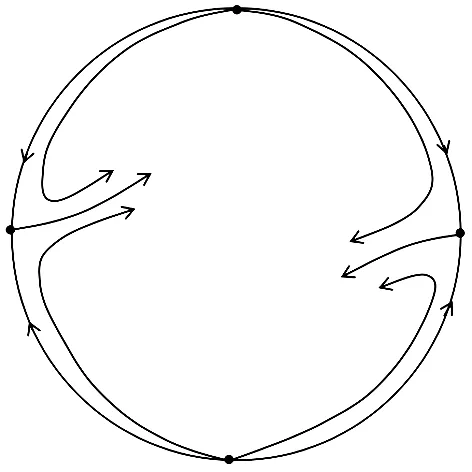
3 主要结果的证明








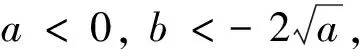



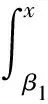


4 数值仿真与讨论