基于排队论的机场上客区系统效益优化研究

李美玉 李倩 张天宇 王浩华*

(1.海南大学 经济学院，海口，570228；2.海南大学 理学院，海口，570228；3.海南大学 信息与通讯工程学院，海口，570228)

1 引言

出租车作为可供机场到港乘客选择的最主要的交通方式之一，近年来受到了广泛的研究.目前，相关研究主要集中在提高出租车通行能力以及管理模式等方面.其中，在组织管理优化方面，黄岩等[1]通过实地调查虹桥机场 T2 航站楼的出租车上客点，对虹桥机场出租车上客点的组织管理方式进行研究，提出了不同发车方式切换的阈值以及减少人车之间相互干扰的措施等,可供机场出租车上客点的规划设计及运营管理工作参考.在服务水平评定方面，耿中波等[2]通过仿真模型 VISSIM对比研究了北京首都国际机场 T3 航站楼出租车上客区的现行方案与备选方案，并对备选方案进行了综合评价，为备选方案的最终取舍提供依据.在管理模式方面，吴娇蓉等[3]通过采用交通仿真技术，分析了不同管理模式下出租车上客区的通行能力和集疏乘客效率，从而得出不同管理模式的适用条件.在通行能力研究方面，孙健等[4]对单车道离港出租车上客系统通行能力的影响因素进行了仿真研究，以浦东机场 T1 航站楼出租车上客区为考察对象，建立了基于 GPSS/JAVA 的仿真模型，并基于仿真模型进行了一系列实验，从而得出可实现通行能力较高的上车点个数.

迄今为止，关于提高机场出租车乘车效率的量化措施还鲜有研究，尽管已有该领域的部分学者提出设定最优上车点个数的量化方法，但建立模型所考虑的因素可能较单一，造成结果的片面性.在提高乘车效率的过程中，机场、乘客与出租车司机三方均在进行博弈，因此要充分权衡各方利弊.本文以北京首都机场的出租车上客区为考察对象，运用排队论的思想来探究如何设置上车点的数量使总的乘车效率最高.将乘客在上车点乘出租车离开机场看作一个排队系统，本文建立了出租车与乘客均在上车点接受“服务”的双端排队模型，此外还综合考虑了各方成本(包含乘客与出租车司机等待时所付出的时间成本以及上车点的建设成本)，进而建立成本优化模型，最终得出的最优上车点个数同时实现了乘车效率最高与总成本最低.

2 双端排队模型的建立

将乘客在上车点乘出租车离开机场看成一个排队系统，并且将此排队系统看成是出租车与乘客均等待在上车点接受“服务”的双端排队系统，即出租车与乘客均作为“顾客”，将上车点比作“服务台”.这时可以得到两个排队模型，即出租车在上车点接受服务以及乘客在上车点接受服务.此外，考虑用机场乘客与出租车各自的排队长度以及等待时间来衡量乘车效率，等待时间取决于排队长度，因此为使乘车效率达到最高，应考虑如何合理设置上车点的数量，使两排队模型的排队长度尽可能减小.

2.1 出租车到达情况的量化分析

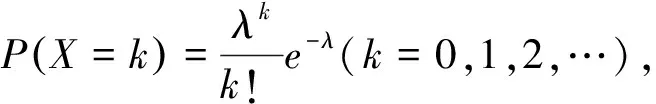
继而通过查询北京首都机场一天内到达上客区的出租车流量，可得到每半小时到达的出租车数量为203辆，即出租车的平均到达率为λ=203辆/半小时.

2.2 乘客到达情况的量化分析

由于排队论中参数λ的含义为单位时间内到达的顾客数，又某时间段内所到达的航班数量是可观测的，亦即单位时间内到达上车点的乘客数是可具体估测的值.具体量化过程见下文.

2.2.1 Logit模型分析选乘出租车乘客占比

本文采用Logit模型对到港乘客选择不同的交通方式占比进行分析.Logit模型的原理为乘客偏向于选择对自己效用最大的交通方式.结合北京首都机场的相关信息，模型的具体建立步骤如下：

a)确定交通选择方式以及作出选择的影响因素：可供机场乘客选择的交通方式主要有机场巴士、出租车、地铁以及自备车；综合考虑目前各交通方式的运营状况，此处提取的评价指标有出行距离、便捷性、等候乘车时间、乘坐时间、乘坐舒适性，分别记为C1,C2,C3,C4,C5,C6.

b)综合评定得到比较矩阵并计算第j个影响因子所占的比重：借鉴层次分析法中两个影响因素重要性比较的标度方法，如表1.

表1

首先以出租车为例，得到影响乘客选择交通方式因素的比较矩阵A,如下：

再计算各因子所占权重，即计算比较矩阵A最大特征根λmax以及最大特征根所对应的特征向量,其中计算特征向量的方法有特征根法、和法、根法、幂法等，此处采用和法计算权重,公式如下：

MATLAB求解结果如下：

类似可得另外三种交通方式的权重向量如下：

c)确定各交通方式评价指标值Ui(α)以及不同交通方式的总体效用值.

首先定义乘客选择第i种交通方式的概率表达式为

Pi(α)=pro[Ui(α)>Uj(α)],

此处借鉴有关学者[15]经研究定义的多元Logit模型，如下：

(2.1)

其中：

Vi=w1Xi1+w2Xi2+…+wkXik，

(2.2)

X与ω分别表示影响乘客选择交通方式的因素及其所占权重.

通过实际调研资料，得出不同交通方式各指标的具体值，如表2.

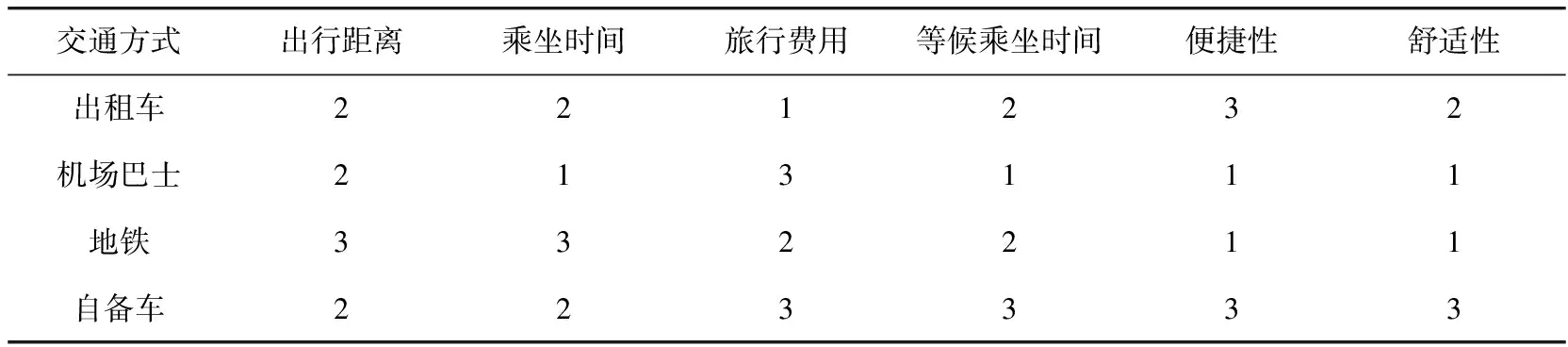
表2 不同交通方式指标表

根据式(2.2)对北京首都机场各交通方式的总体效用值进行计算，结果如下：

出租车：

Vt=0.292×2+0.401×2+0.095×1+0.045×2+0.131×3+0.037×2=2.03,

同理可得另外三种交通方式的总体效用值如下：

机场大巴：Vb= 1.87；地铁：Vs= 2.4763；自备车：Vp=2.596.

基于上述各交通方式的总体效用值计算结果，结合式(2.1)，可得到乘客选择各交通方式的占比情况，其中选乘出租车的占比情况如下：

2.2.2 单位时间内到达上车点乘客数量的确定

带班育人是班主任最基本的实践活动，这些活动是增长班主任才干的广阔舞台。有专业理想的班主任要争取尝试不同地区、不同学段和不同类型的班级，“遍历”各种情境。通过带班实践,师生朝夕相处，既可以培养班主任献身教育事业、热爱学生的高尚品德，也可以培养班主任的工作能力。

通过对一天内各时段的北京首都机场旅客数量进行统计，再结合上述求得的选择出租车的乘客数量所占的百分比为19.29%，从而得到单位时间内到达上车点的乘客数量为λ=1319人/小时.

2.3 服务时间分布研究

假定服务时间t服从负指数分布，其分布密度函数如下：

用极大似然估计，可以求得μ的估计值为

μ在排队系统中所代表的含义为服务率，依据上式，其估计值为平均服务时间的倒数.用上客区的通行能力来表示服务率，通过查询北京首都机场的相关数据以及假定平均每辆出租车载客两名，可得：

①当出租车作为“顾客”在上车点接受服务时，其服务率μ=756辆/小时；

②当乘客作为“顾客”在上车点接受服务时，其服务率μ=1512人/小时.

3 双端排队模型的求解

对于该出租车与乘客的双端排队模型，无论是出租车作为“顾客”亦或是乘客作为“顾客”得到的两个排队模型均为多服务台模型.

其中，s为服务台个数，p0为系统中没有顾客的概率，其计算公式如下：

ρ是系统中至少有一个顾客的概率，亦即服务台处于忙的状态的概率，其计算公式如下：

故有

由平均排队长度Lq可求得系统中平均顾客数L：

L=Lq+ρ,

系统中顾客的平均逗留时间

系统中顾客的平均等待时间

在“出租车—上车点”排队模型中，分别求出当上车点个数，即s分别为4，5，6时各自的Lq,L,W,Wq数值进行比较，结果见表3.

表3 系统各服务指标

与此同时，对于多服务台系统，其系统中有k辆车排队的概率如下：

同样分别求出当上车点个数，即s分别为4，5，6时，有k辆出租车排队的概率，结果如表4.

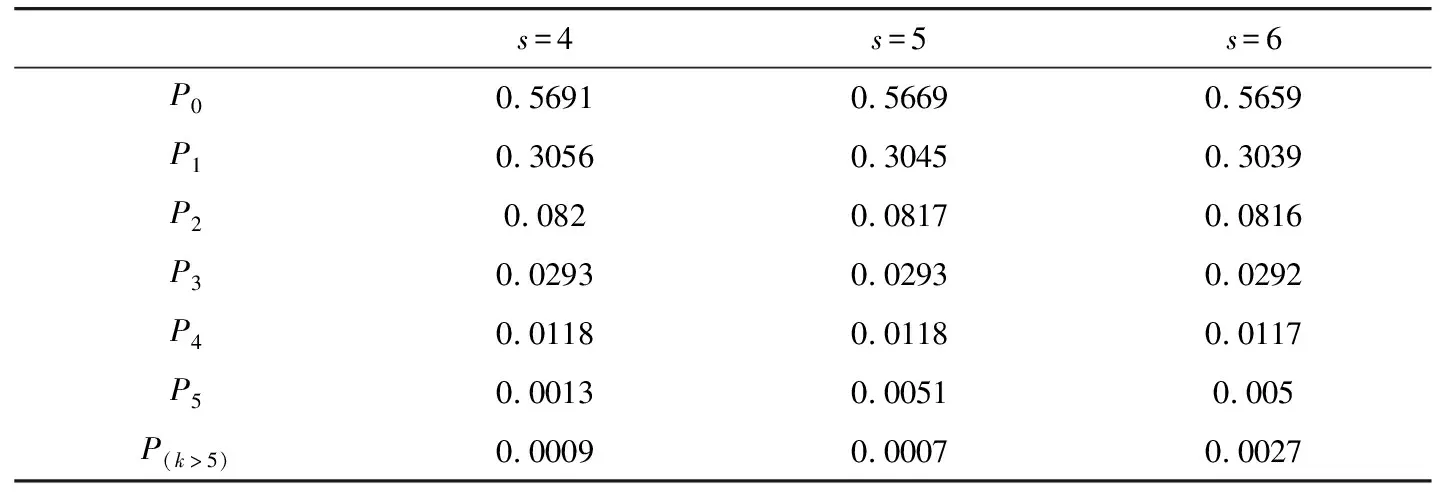
表4 系统中有k辆出租车排队的概率

从表3数据分析得，随着上车点数量的增加，系统各服务指标呈现下降趋势，因此上车点的增加对系统服务有积极影响.并且设5个上车点时，整个系统的性能改善比建设4个上车点明显，但建设6个上车点比建设5个上车点的各性能指标改善并无明显作用.由表4数据可知，建设5个上车点时系统超过5辆车排队的概率最小，当再增加一个上车点时，其概率反而增大，因此建设5个上车点是最合理的选择.

同理，在“乘客—上车点”排队模型中运用同样的方法，可以得到建设8个上车点是最合理的选择.

4 模型验证与优化

4.1 成本优化模型的建立

由于在机场建设上车点需要一定的建设成本，而出租车与乘客等待时需要付出时间成本，故最理想的情况是在保证乘车效率达到最高时总成本也可保证最低.

在平稳状态下单位时间内总成本之和的平均值为

C=c′ss+cwL,

(4.1)

其中，c′s为单个上车点的建设成本，cw为出租车或乘客等待过程中需要付出的单位时间成本，则目标函数为

minC=c′ss+cwL,

约束条件为

将式(4.1)代入上述约束条件，整理后得

(4.2)

4.2 成本优化模型的求解

4.2.1 “乘客—上车点”排队模型成本优化求解

模型中各指标值如表4，其中考虑到机场出租车上车点的建设成本较高，故将式(4.2)中的单位成本比定为1∶1000.

表5 模型指标值

利用上述成本优化模型对北京首都机场的“乘客—上车点”排队模型进行优化求解，计算结果如下.

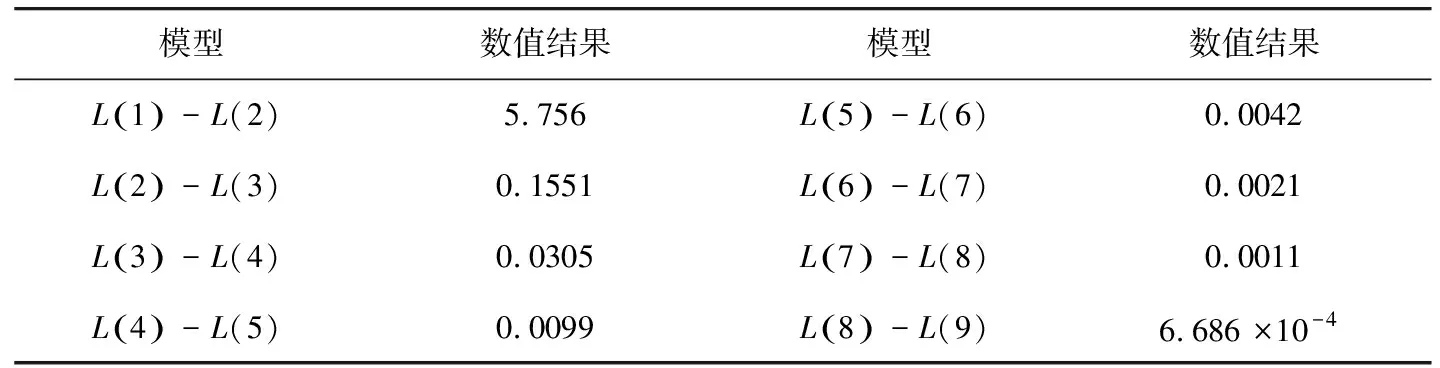
表6 计算结果

由上述计算结果可知，当s=8时，满足式(4.2)，亦即使乘客等待成本与服务台建设成本之和达到最小.

4.2.2 “出租车—上车点”排队模型成本优化求解

与上述求解过程同理，在“出租车—上车点”排队模型中，满足出租车司机等待成本与服务台建设成本之和最小的上车点个数为5个.

4.3 模型验证与优化结果分析

在为使乘车效率达到最高时,“乘客—上车点”排队模型中最优上车点个数为8个，“出租车—上车点”排队模型中的最优上车点个数为5个.这与总成本达到最低时的双端排队模型优化求解结果相一致.因此这极大程度上验证了上述所建双端排队模型的合理性与优越性.最后，考虑到出租车是为乘客服务的，故双端排队模型中顾客满足程度权重比可考虑定为出租车司机：乘客=30%：70%，因此可得最优上车点个数为7个.

5 结语

本文以北京首都机场出租车上客区的乘车效率为研究对象，基于排队论的思想建立了出租车与乘客的双端排队模型.此外，建立的成本优化模型对上述双端排队模型进行了验证与优化，因此可得出本文所建议的设置7个上车点的结论不仅可以使总的乘车效率达到最高，而且还能做到总成本最低.

本文的结论不仅适用于北京首都机场的出租车上客区，也适用于其他枢纽内单车道单通道的出租车上客系统，即当考察对象发生变化时，只需变换对应的参数值，即可得出最优上车点个数.此外，可以通过修正出租车司机与乘客的满意度权值的相对大小来协调出租车司机与乘客的利益冲突；同理，也可通过修正出租车司机与乘客的时间成本与上车点服务台的建设成本权值的相对大小来协调出租车司机、乘客与机场的利益冲突.然而，需要指出的是，本文在求解参数时所利用的数据仅为一天内北京首都机场的相关数据，当客流量波动较大时，如春节等节假日期间与正常工作日的客流量差别很大，所得结果可能具有一定的误差和片面性，因此在进一步的研究中可通过对比分析不同时期客流量波动所造成的不同影响，进而对结果进行修正，得出更具有一般性的结论.