桥隧段风屏障对高速列车气动荷载及行车安全的影响

施成华 王昂 邓锷 杨伟超 何旭辉

(中南大学土木工程学院，湖南长沙410075)

随着我国西部地区高速铁路建设的大发展，桥隧相连段 (隧道-桥梁-隧道)已是西部高铁线路中常见的形式，桥隧占比有的甚至高达70%，如西成客运专线秦岭段和大巴段的桥隧比高达到99.3%和81.1%［1-2］。特殊的山谷地形易产生强横风，列车在强横风下的桥隧相连段行驶时，气动性能剧烈突变，气动安全性降低［3-4］。为保证高速列车在桥隧相连段的安全运行和桥梁的稳定性，通常在桥梁上设置风屏障作为主要的防风措施［5］。

近年来，国内外诸多学者对高速列车的空气动力学特征和运行安全性进行了一系列的研究。Avila-Sanchez等［6-7］分析了铁路桥梁上装有不透风式挡风墙时桥梁上的流场分布情况;何旭辉等［8］通过改变雷诺数、挡风墙高度、透风率及风偏角等参数，对列车气动性能进行研究，发现桥上列车的侧力和力矩系数会随挡风墙高度的增加而增大，而升力系数变化并不明显;王英学等［9］建立了高速列车空气动力学分析系统，研究了高速列车突入隧道时产生的气动效应;邓锷等［10-11］针对洞口横风环境下高速列车突入隧道过程中车体的气动特性及其对行车安全的影响进行了研究;Deng等［12-14］研究发现高速列车在横风环境下驶入 (驶出)隧道时，车身同样会出现剧烈的气动突变效应，严重威胁列车运行安全;张洁等［3］通过数值模拟研究了高速铁路桥梁上透风式挡风墙高度对列车气动性能的影响，结果表明，桥梁挡风墙合理高度为2.8 m;李燕飞等［15］研究了开孔式挡风墙的开孔率对横风下高速列车气动性能的影响，得出透风率为30%的挡风墙下运行动车组的横向气动性能最好。

由国内外研究现状可知，大多数学者以研究合理设置桥梁风屏障和列车在桥梁上或者进出隧道过程的气动效应、行车安全性为主，但对于桥隧相连段设置风屏障后，列车在由隧道驶入桥梁(“出”隧道)或由桥梁驶入隧道(“进”隧道)过程中的气动特性和行车安全性的研究相对较少，而此过程中气动效应突变，控制着列车的运行安全性。因此，本文以郑万高铁红梁湾大桥为工程背景，基于计算流体力学湍流模型和多孔介质理论，建立列车-隧道-桥梁-风屏障三维CFD(计算流体力学)数值模型和风-车-轨-桥动力耦合分析模型，研究风屏障对高速列车运行在桥隧相连段时气动荷载的影响以及列车轮重减载率和脱轨系数的变化特性，探讨了桥隧相连段设置风屏障对列车行车安全性的影响。

1 数值模拟方法

1.1 基本理论

1.1.1 湍流模型

本文研究的高速列车的最高运行速度约为350km/h，其运动的马赫数 (Ma=0.286)小于0.3，将空气视为不可压缩的。高速列车附近流体的雷诺数达2×107，列车周围流场处于高度湍流状态。RNG·k-ε湍流模型能够有效改善湍流耗散率的精度，并且考虑了湍流旋涡，能够较好地模拟列车周围的湍流结构，提高了计算精度，计算效率较高，被广泛应用于高速列车流场结构数值模拟中［3，10-14，16］，因此本文采用 RNG·k-ε 湍流模型进行数值模拟研究。

考虑到空气不可压缩，则湍流平均连续性方程、动量守恒方程表示如下:

式中:xi、xj为不同方向的位移;ρ为流体密度;和j为雷诺平均气体的速度分量;t为时间;p¯为雷诺平均流体微元体压力;υ为运动粘性系数;为雷诺平均体积力;为雷诺平均脉动速度;是由湍流脉动所造成的应力，称为Reynolds应力。

1.1.2 多孔介质模型

多孔介质模型是在动量方程中增加了一个代表动量消耗的源项。源项包括粘性损失项和惯性损失项。动量源项对多孔介质区域的压力梯度有影响，对于各向同性的多孔介质，动量源项可表示为

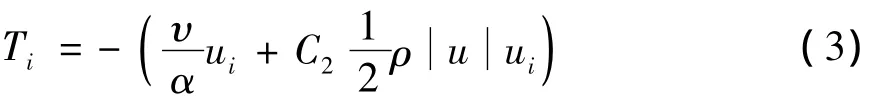
式中:α为渗透系数;C2为惯性阻力系数;u为速度的绝对值;ui为气体的速度。

模拟在高速流动中的多孔板时，可以忽略渗透项，只考虑惯性阻力系数，根据经验公式推导出垂直平板平面方向的惯性阻力系数:

式中:Af为孔的总面积;Ap为板的总面积;当h/d＞1.6(d为孔直径，h为板厚度)且Re＞4000时，系数C约为0.98。

1.2 数值模型

1.2.1 几何模型

几何模型按照1∶1的比例建立，列车几何模型是我国的CRH3型高速列车。根据相关研究［16］，3节车辆编组列车的气动安全性能够适用于3节以上车辆编组列车的气动安全性评估，因此，列车模型均采用3节车厢 (头车、中车、尾车)来模拟列车的实际运行，并对其进行适当简化，忽略受电弓、车窗和转向架等部件。桥梁几何模型是我国高速铁路中常用的32 m预应力混凝土简支箱梁桥;风屏障采用厚度为0.1 m、高为3 m的多孔介质薄板，透风率为30%;隧道采用双线标准隧道断面，其内轮廓面积为100 m2，相应阻塞比为0.149。列车、桥梁及风屏障的几何简化模型具体参数详见图1。桥隧相连段由桥梁连接两隧道组成 (隧道-桥梁-隧道)，两条隧道长度均为200 m，桥梁长度为159m。

1.2.2 模型网格

计算模型统一采用结构化网格，共划分3个区域:动网格区域、静网格区域和多孔介质模型区域。列车的运动通过动网格铺层法实现，风屏障的透风率通过调节多孔介质模型的参数实现，而动网格和静网格之间以及多孔介质区域和静网格之间用交界面进行连接。为了充分考虑列车附面层效应，将车体表面附近的网格设置成8层，并进行加密处理，首层厚度为0.001m。模型总网格数量约为416万。模型网格如图2所示。

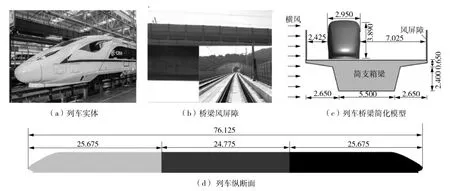
图1 几何简化模型 (单位:m)Fig.1 Geometric simplification model(Unit:m)

图2 模型网格Fig.2 Model grid

1.2.3 边界条件

本文CFD数值计算模型包含有4种边界条件:壁面、交界面、压力出口和压力远场。列车表面、隧道壁面、桥梁表面及地面都设置为无滑移壁面边界;桥梁上开阔空间的边界条件设置为压力远场，实现横风的加载;不同网格区域之间采用交界面连接，进行能量和数据的传递。列车运动初始开阔空间和隧道进出口设置为压力出口。模型边界条件如图3所示。

1.3 气动荷载计算

1.3.1 列车气动荷载

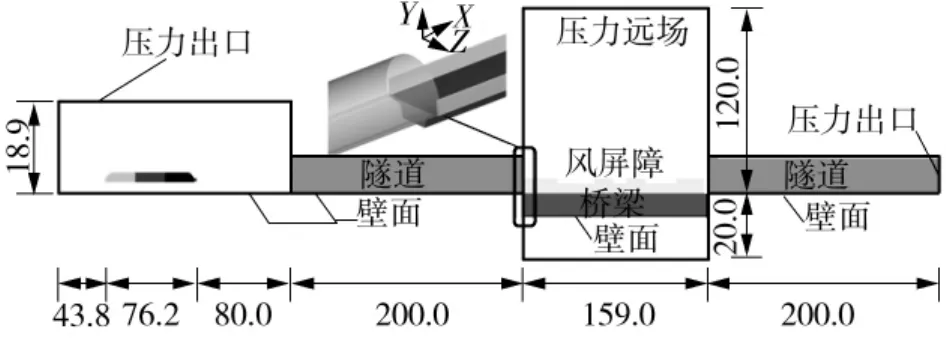
图3 模型纵断面和边界条件 (单位:m)Fig.3 Longitudinal section of the model and boundary conditions(Unit:m)

列车运行时受到的阻力Fx主要引起列车的能耗，对行车安全性影响较弱。因此本文主要研究横向力Fz、升力Fy、倾覆力矩Mx、偏航力矩My和仰俯力矩Mz的变化特征。列车所受到的气动荷载如图4所示。

图4 列车气动荷载示意图Fig.4 Schematic diagram of train aerodynamic load

在计算气动荷载时，将列车规则划分为若干段，并提取每一段的平均静压时程数据，可得列车气动荷载计算公式:

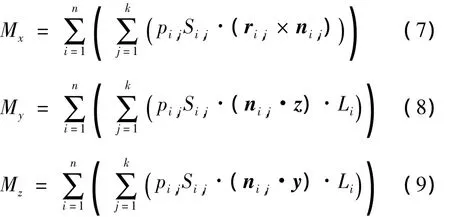
式中:k、n分别表示车身表面在环向、纵向上的分段数量;pi，j和 Si，j分别表示计算面 (i，j) 的平均静压和面积;ni，j为计算面 (i，j)的单位外法向量;y和z分别为沿y和z方向的单位向量;ri，j表示纵向第i横断面上的力臂向量;Li表示计算面(i，j)中心至车厢重心O的纵向距离。

1.3.2 桥梁气动荷载

桥梁的气动阻力、仰俯力矩和偏航力矩对桥梁稳定性影响较小，本文主要研究桥梁的横向阻力Fzb、气动升力Fyb和倾覆力矩Mxb的变化特征。在计算桥梁气动荷载时，需要考虑风屏障对其的影响，而将风屏障作为桥梁的一部分。将桥梁和挡风墙仍进行分段处理，可得桥梁气动荷载计算公式:

式中:l、m分别表示风屏障及桥梁在环向、纵向上的分段数量;mi，j为风屏障和桥梁计算面 (i，j)的单位法向量。

1.4 网格独立性检验

为检验模型网格的独立性，本文设置了不同网格尺寸的模型，网格总数分别为:200万 (粗)、400万 (中)、600万 (细);以400万网格单元模型为基础，附面层网格层数设置4、6、8、10。列车运行于设置风屏障的桥隧相连段时，以各节车厢的倾覆力矩的最大值Mx，max为检验指标，计算结果如图5所示。结果表明网格数量400-600万和附面层8-10层情况下的计算结果收敛性较好，故本文选择400万网格数量和8层附面层能够满足计算精度要求。

1.5 模型结果验证

图5 网格独立性检验Fig.5 Grid independence test

Dorigatti等［17］的研究表明，在一定风向角范围内，动态模型数值模拟与风洞静态试验在气动载荷的三分力系数方面是一致的。为验证本文数值模拟结果的准确性，建立与张佳文等［18］的风洞试验相似的数值模型 (风屏障高4m，透风率为30%，风速为15 m/s，风向角为90°，列车位于迎风侧)，如图6所示，模型缩尺比为1∶20。采用本文的RNG湍流模型和多孔介质模型理论，以CRH3型列车各节车厢的升力系数与张佳文等［18］的风洞试验结果进行对比，如表1所示。

图6 几何模型Fig.6 Geometric models

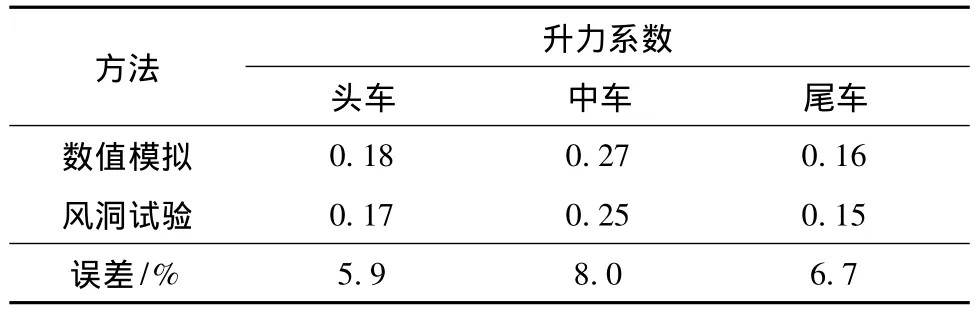
表1 数值模拟与风洞试验结果对比Table 1 Comparison of results between simulation and test

由表1可知，数值模拟与风洞试验得到的升力系数较为接近，误差在10%以内，本文选取的数值模型理论和计算方法可靠度较高。

2 风-车-轨-桥动力耦合模型

2.1 动力耦合模型

根据朱志辉等［19］提出的列车-轨道-桥梁耦合系统动力分析混合算法，模型耦合系统分为列车-轨道耦合系统和桥梁子系统。两个系统通过轨道和桥梁在连接节点处的相互作用力连接耦合起来，将计算得到的列车和桥梁气动荷载分别输入列车轨道子系统和桥梁子系统，实现风-车-轨-桥的动力耦合分析，模型如图7所示。

图7 列车-轨道-桥梁耦合系统示意图Fig.7 Schematic diagram of train-rail-bridge coupling system

列车和轨道通过轮轨接触关系耦合为列车-轨道子系统，列车-轨道子系统的耦合时变动力方程为

式中:Mvv、Cvv、Kvv分别为列车子系统的质量矩阵、阻尼矩阵和刚度矩阵;Mrr、Crr、Krr分别为轨道子系统的质量矩阵、阻尼矩阵和刚度矩阵;Kvh和Krr1分别为轮轨间接触引起的车辆刚度附加矩阵和钢轨刚度附加矩阵;Krr2和Crr2分别为扣件刚度引起的钢轨刚度附加矩阵和阻尼附加矩阵;Kvr和Krv分别为列车、轨道刚度耦合项;Fv和Fr分别为列车、轨道的荷载向量;Xv、X·v、X¨v分别为列车子系统的位移、速度和加速度向量;Xr、X·r、X¨r分别为轨道子系统的位移、速度和加速度向量。

采用直刚法建立桥梁子系统动力方程:

式中:Mbb、Cbb和Kbb分别为桥梁子系统的质量、阻尼和刚度矩阵;Xb、X·b、X¨b和 Fb分别为桥梁子系统的位移、速度、加速度和外荷载向量。

列车气动荷载Fvt=[0 FyFzMxMyMz]T，vtyzxyz耦合于列车荷载向量Fv中，而桥梁气动荷载Fvb=[0 FybFzbMxb0 0]T，耦合于桥梁外荷载向量Fb中，实现风-车-轨-桥的动力耦合模型计算分析。

列车-轨道子系统与桥梁子系统间通过梁轨间的相互作用力实现耦合，桥梁对钢轨的作用力Frb为

钢轨对桥梁的作用力Fbr为

2.2 动力耦合模型计算流程

采用Newmark-β法求解桥梁子系统和列车-轨道耦合子系统动力方程。车、桥气动荷载和列车-轨道耦合子系统具有时变性，分析过程中每一步根据列车所处不同位置进行相应的更新，采用Matlab软件迭代计算。风-车-轨-桥动力耦合系统的计算流程如图8所示，其中t为列车运行时间。

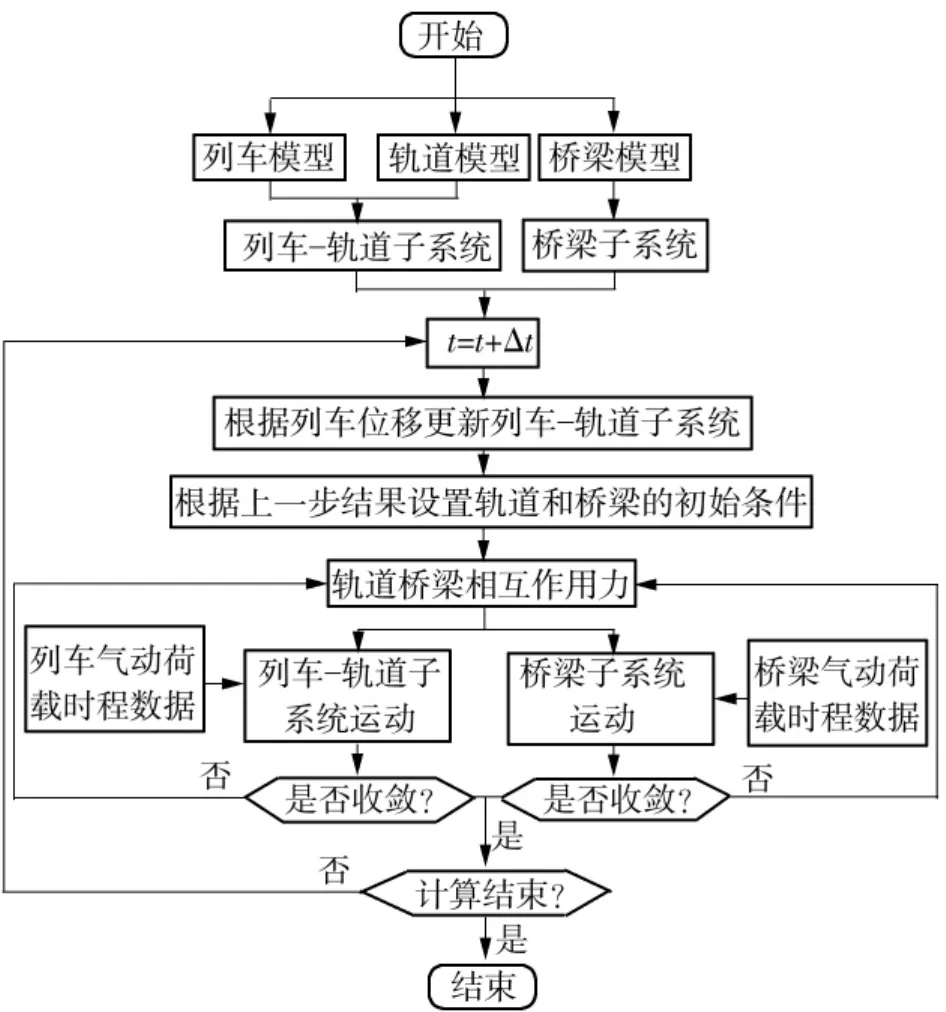
图8 风-车-轨-桥动力耦合系统计算流程图Fig.8 Calculation flowchart of wind-train-rail-bridge dynamic coupling system

3 风屏障对列车气动荷载的影响分析

为清晰对比分析有、无风屏障条件下列车在桥隧相连段运行过程中气动荷载的差异，现以头车为例(其中车速为250 km/h，横风风速为25 m/s;风屏障透风率为30%，高度为3.0 m)，绘制了列车运行桥隧相连段过程中头车气动荷载的时程曲线，如图9所示。同时，为更直观反应气动荷载的变化对车厢运行姿态的影响，绘制了相应的头车“进”、“出”隧道过程中各车厢运行姿态的变化图(“出”表示车头鼻尖驶出隧道至车尾鼻尖驶入桥梁的过程(t=4.03～5.13s);“进”表示车头鼻尖驶入隧道至车尾鼻尖驶离桥梁的过程 (t=6.32～7.42 s))。各节车厢气动荷载突变幅值及峰值统计如表2所示。

分析图9和表2可知:

图9 有、无风屏障条件下头车气动荷载和车厢运行姿态的对比Fig.9 Comparison of aerodynamic load of the head car and movement posture of the carriage with or without wind barrier

表2 有、无风屏障条件下气动荷载突变幅度和峰值对比Table 2 Comparison of the amplitude of aerodynamic load abrupt change and the peak value with or without wind barrier

(1)无论是“进”或“出”过程，无风屏障条件下各节车厢气动荷载均发生显著突变;而有风屏障条件下，相应气动荷载突变幅度均显著下降，且降幅均达50%以上，相应的气动荷载突变速率也相对较为平缓 (由图9中时程曲线突变斜率可知)。以头车为例，横向力、升力、倾覆力矩、偏航力矩和仰俯力矩在“出”隧道过程中分别下降了89%、86%、89%、62%和52%，在“进”隧道过程中分别下降了89%、87%、89%、57%和67%。

(2)无论是“进”或“出”隧道过程，各节车厢的横向力和倾覆力矩受风屏障的影响最为显著，相应的突变幅值均降低88%以上。以倾覆力矩为例，头车、中车、尾车在“出”隧道的过程中降幅分别为89%、94%和88%;在“进”隧道的过程中降幅分别为89%、92%和91%。仰俯力矩受风屏障的影响相对较弱，降幅在52%～81%之间。

(3)列车在桥梁上运行时，各节车厢气动荷载 (绝对值)的峰值在有风屏障的条件下也有显著的降低，其中横向力和倾覆力矩降幅最大，头车、中车、尾车的横向力降幅依次为91%、93%和92%;而仰俯力矩降幅相对较小，头车、中车、尾车降幅分别为42%、54%和17%。这一现象与列车在“进”、“出”隧道过程中气动荷载对风屏障的敏感性反应一致。

4 风屏障对行车安全性的影响分析

4.1 脱轨系数

本文根据《高速铁路设计规范试行》(TB10621—2009)和 GB 5599—85［20］规范，桥隧相连段列车的脱轨系数 (DC)的安全界限值采用Q/P≤0.8(Q和P分别为某一时刻作用在车轮上的横向力和垂向力)或Q/P＞0.8的最大持续时间小于0.05s的标准。

图10为车速为250km/h、横风风速为25m/s、风屏障透风率为30%、高度为3.0m条件下，列车在有、无风屏障条件下运行时各轮对的脱轨系数时程曲线。

分析图10可知:

(1)在无风屏障条件下 (如图10(a)、(b)和 (c))，各节车厢的各轮对背风侧DC波动范围明显大于迎风侧，且超限频率高、累计时间长，无风屏障下头车1号轮对迎风侧和背风侧的DC峰值分别为0.78和2.18;而在有风屏障的条件下 (如图10(d)、(e)和 (f))，除了头车的1、3号轮对在“进”、“出”过程中DC出现突变和瞬时超限情况，其余各轮对的DC值波动均在0.25以内。

根据图9所示的气动荷载时程曲线和列车运行姿态可知产生该现象的原因:无风屏障条件下，列车受到横风的影响显著，使各节车厢向着背风侧倾斜，背风侧车轮所受横向力大于迎风侧车轮的，在风荷载和轮轨不平顺性联合作用下，车轮所受横向力波动，从而导致DC值随列车的运行波动变化，背风侧车轮瞬时冲击轨道现象较迎风侧严重，背风侧DC值的波动幅度更大;而在有风屏障条件下，由于风屏障对列车的防护作用，车厢无明显倾斜现象，迎风侧和背风侧车轮所受横向力基本一致，从而DC波动幅度无明显差异，且波动峰值较无风屏障条件下显著降低。

(2)在有风屏障的情况下，头车的DC值是控制整个列车运行安全的关键，尤其是头车1、3号轮对上的DC值。如图10(d)、 (e)和 (f)所示，列车在有风屏障的桥隧相连段行驶时，仅头车1、3号轮对出现突变现象，波动峰值超限，最大超限持续时间满足相关规定;2、4号轮对DC值则在0.25内波动。头车的DC最大值出现在背风侧1号车轮 (1.64)上，其次是背风侧3号车轮(0.82)。原因可能是1、3号轮对在几何位置上均处于头车前、后转向架的前端，易出现车轮踏面与轨道顶面紧密接触碰撞的情况，而2、4号轮对在转向架悬挂系统的缓冲作用下仍能保持平稳运行。

4.2 轮重减载率

仅用脱轨系数无法完全反映列车的运行安全性，如列车所受横向力很小 (或者没有)，车轮的上下振动也可能发生横向相对位移而脱轨，所以还需轮重减载率 (RR)作为评判行车安全性的另一个安全指标。本文采用翟婉明等［21］提出的新型轮重减载率评判准则，即:ΔP/¯P≤0.60(ΔP是减载侧车轮的轮重减载量，¯P是轮对的平均静轮重)，或者ΔP/¯P＞0.60的最大持续时间小于0.035s。

图11给出了车速为250 km/h、横风风速为25m/s、风屏障透风率为30%、高度为3.0 m条件下，有、无风屏障时各节车厢轮重减载率时程曲线(当RR＞1时，车轮与轨道分离)。

分析图11可知:

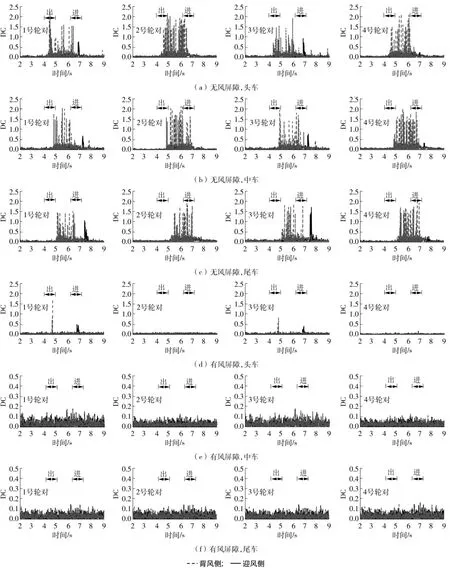
图10 有、无风屏障条件下列车脱轨系数时程曲线Fig.10 Time-history curves of derailment coefficient with or without wind barrier

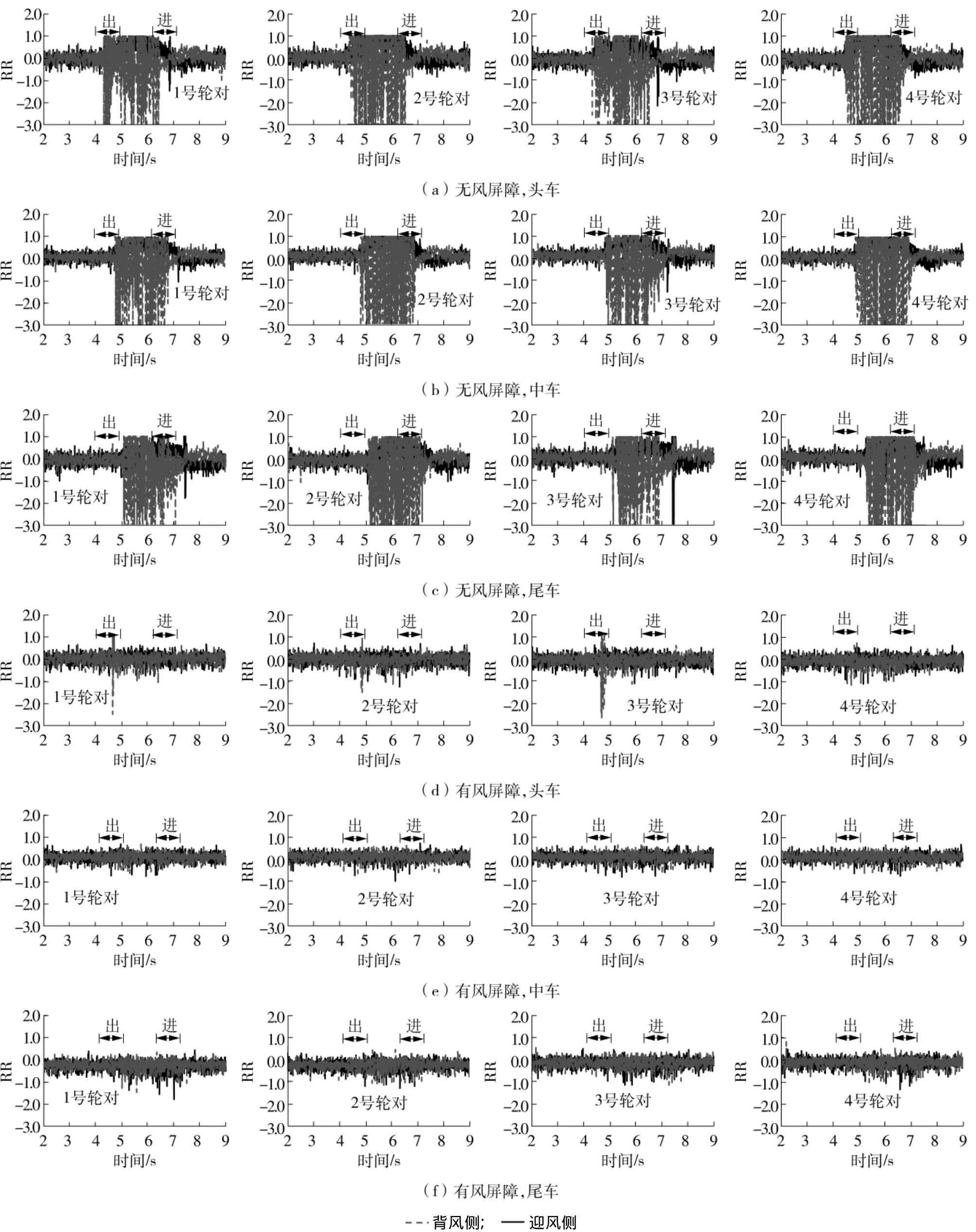
图11 有、无风屏障条件下列车轮重减载率时程曲线Fig.11 Time-history curves of wheel weight reduction rate with or without wind barrier

(1)通过对比有、无风屏障下的RR时程曲线，可得到与4.1节相似的结论:桥隧相连段设置风屏障可以显著降低各轮对的RR值，迎风侧和背风侧各轮对 (除了头车1、3号轮对外)的RR波动幅度相同;头车RR值对整个列车运行的行车安全性也起控制作用，尤其是头车1、3号轮对的。当列车运行至桥隧相连段时，无风屏障条件下(如图11(a)、 (b)和 (c)所示)，RR值超过0.6的频率较高，最大超限持续时间为0.45 s，已超出安全限值;背风侧的RR值波动范围明显大于迎风侧 (原因4.1节已说明)，背风侧RR值波动的整体趋势低于迎风侧，说明横风作用下列车向背风侧倾斜，背风侧所受轮轨接触力较大;而在有风屏障的条件下 (如图11(d)、(e)和 (f))，中车和尾车的RR值波动幅度范围较小，峰值均未超过0.6，且迎风侧和背风侧无明显差异。头车的运行姿态受横风、列车风和风屏障的共同影响较大，头车RR值的波动峰值出现超过0.6的情况，头车背风侧1、2、3号车轮的RR值超限的持续时间分别为0.015、0、0.001s(0s为瞬时超限)，列车处于安全运行状态。

(2)列车在有风屏障的桥隧相连段运行时，“出”隧道过程中列车运行安全性较“进”隧道过程中低。如头车在“出”隧道过程中的DC突变峰值大于“进”隧道过程，如图10(d)所示，头车1号轮对“出”隧道过程的DC峰值为1.64，“进”隧道过程的为0.71;3号轮对“出”隧道过程的为0.84，“进”隧道过程DC峰值为0.48(上述情况最大超限持续时间均满足相关规定)。如图11(d)所示RR时程曲线，头车1、2、3号轮对在“出”隧道过程中RR出现大于0.6的突变值，而在“进”隧道过程中，RR在0.6以内波动，无突变现象。出现上述现象的原因可能是:“出”隧道过程中列车由行车安全性较高的隧道驶入安全性较低的桥梁段，突然受到横风影响，列车运行姿态变化复杂 (变化步骤多、幅度大)，并向背风侧倾斜，行车安全性降低，而“进”隧道过程中列车运行姿态恢复至平衡位置，再次驶入行车安全性较高的隧道，列车安全性得到提高。

综上所述，桥隧相连段设置风屏障后:①列车运行安全指标 (脱轨系数和轮重减载率)显著降低，迎风侧和背风侧各轮对 (除了头车1、3号轮对外)安全指标波动幅度基本相同;②头车的安全指标对整个列车运行的安全性起控制作用，尤其是头车转向架的前轮 (即1、3号轮对);③列车“出”隧道过程中行车安全性较“进”隧道过程中低。

5 结论

本文基于列车-隧道-桥梁-风屏障的三维CFD数值模型和车-轨-桥的动力耦合分析模型，建立了风-车-轨-桥耦合动力一体化计算模型，研究了高速列车通过隧道-桥梁-隧道路段过程中列车的各节车厢的气动荷载以及各轮对安全指标的变化特性，探讨了桥隧相连段设置风屏障对列车运行安全性的影响，主要得到如下结论:

(1)设置风屏障后，各节车厢的气动荷载突变幅值显著降低，降幅基本均在50%以上;其中横向力和倾覆力矩受风屏障的影响最为显著，降幅高达88%以上。

(2)设置风屏障后，列车运行安全指标 (脱轨系数和轮重减载率)显著降低，行车安全性提高;迎风侧和背风侧各轮对 (除了头车1、3号轮对外)安全指标波动幅度相同。

(3)头车的安全指标对整个列车行车安全性起控制作用，尤其是头车1、3号轮对的。头车的1、3号轮对在几何位置上处于头车前、后转向架的前端，易出现轮踏面与轨顶面紧密接触的情况。

(4)列车由隧道驶入桥梁的过程中行车安全性较由桥梁驶入隧道过程低，“出”隧道过程列车行车安全性是降低的，而“进”隧道过程行车安全性是提高的。