基于天棚模型和扰动观测器的主动悬架滑模控制研究
秦武 康英姿† 上官文斌 任艳
(1.华南理工大学机械与汽车工程学院,广东广州510640;2.宁波润轴汽配有限公司,浙江宁波315800)
汽车悬架系统的振动与噪声直接影响汽车的平顺性[1-2]。传统被动悬架系统的刚度和阻尼是不可调的,很难保证汽车在不同的路面激励下都具有良好的平顺性[3]。区别于传统的被动悬架和半主动悬架,主动悬架在车身与轮胎之间安装了作动器,利用作动器的控制力降低簧载质量的振动。因此,研究主动悬架的控制算法可以改善汽车的振动与噪声。
研究人员提出了多种控制算法,例如模糊控制算法[4]、基因控制算法[5]、神经网络控制算法[6]和滑模控制算法[7]。其中,滑模控制是一种变结构控制,适用于有扰动的非线性系统,对外部的干扰不敏感,具有较强的鲁棒性,被广泛地应用于主动悬架中。Kim等[7]提出了基于天棚模型的主动悬架滑模控制算法,对比了被动悬架和主动悬架的簧载质量加速度,验证了基于天棚模型的悬架滑模控制算法的有效性;Chen等[8]给出了将传统的滑模控制算法和线性二次最优控制算法相结合的优化滑模控制算法;庞辉等[9]和楼少敏等[10]提出了主动悬架滑模控制算法,改善了主动悬架性能。
若存在外部扰动、悬架刚度和减振器阻尼不确定性,则基于天棚模型的滑模控制不适于主动悬架系统的控制。Deshpande 等[11]和 Pusadkar等[12]研究了具有扰动观测器的主动悬架滑模控制算法,利用扰动观测器估算外界扰动以及由悬架刚度、减振器阻尼的不确定性引起的扰动,减小了悬架模型的不确定性和外界扰动对系统的影响。
综上所述,在基于天棚模型的主动悬架滑模控制研究中,大多数研究是将悬架模型中的减振器和悬架弹簧的特性表示为分段线性或者多项式,且将悬架刚度系数和减振器阻尼系数考虑为确定的数值。然而,在工程中,悬架刚度和减振器的阻尼较难准确获得且具有不确定性。在具有扰动观测器的主动悬架滑模控制研究中,文献 [11]的控制目标是主动悬架系统中的簧载质量位移和速度,并没有考虑悬架的动行程。在阶跃位移路面激励下,悬架处在平衡位置时,出现悬架动行程不为零的问题。随着路面激励振幅的增大,悬架动行程也会增大,出现悬架被击穿的现象。
本文考虑了外界的干扰,建立了非线性二自由度模型,提出了基于天棚模型和扰动观测器的主动悬架滑模控制算法,以确保悬架动行程在有限时间内收敛于零的前提下,有效降低簧载质量振动,实现改善汽车平顺性的目的。
1 非线性二自由度主动悬架模型及天棚模型
建立1/4汽车的非线性二自由度主动悬架模型,如图1所示。簧载质量 (ms)为1/4汽车的质量,非簧载质量 (mu)主要包括车轮和转向节的质量。簧载质量与非簧载质量之间是通过悬架弹簧、减振器和作动器相连。轮胎支撑非簧载质量和簧载质量。

图1 非线性二自由度主动悬架模型Fig.1 Nonlinear two degrees of freedom model of active suspension system
图1 中悬架弹簧力、减振器阻尼力、轮胎动载荷、作用于簧载质量上的外界干扰和作动器的作用力分别记为fs、fd、ft、fe和fc。路面的激励位移记为zr,簧载质量和非簧载质量的位移相对于平衡位置分别记为zs和zu。非线性二自由度主动悬架模型中簧载质量和非簧载质量的动力学式为

当轮胎有较大的上下跳动时,轮胎与地面会脱离接触,轮胎动载荷为零。因此,轮胎动载荷的表达式应为
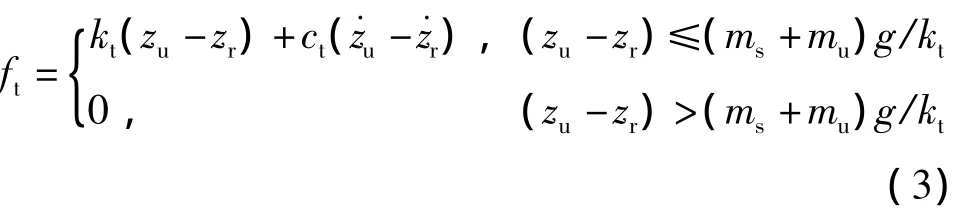
式中:kt为轮胎刚度;ct为轮胎阻尼;g为重力加速度。
在较大振幅的路面激励下,悬架弹簧会碰撞减振器上端的限位块,悬架刚度会急剧变大 (相当于悬架弹簧与限位块并联)。图2为悬架弹簧力(fs)与悬架动行程zsu(zsu=zs-zu)的非线性特性。

图2 悬架弹簧力与悬架动行程的非线性特性Fig.2 Nonlinear characteristic between suspension spring force and suspension deflection
由图2可知,通过2段线性函数拟合悬架的弹簧力与悬架动行程之间的非线性关系,其表达式如下:

式中:k0、k1和k2分别为限位块刚度、第1段线性刚度和第2段线性刚度;a为常数 (拐点)。
图3为减振器的阻尼力 (fd)与悬架相对速度(˙zsu)之间的关系示意图,通过4段线性函数拟合减振器阻尼力(fd)与悬架相对速度(˙zsu)的非线性特性,其表达式为[13]
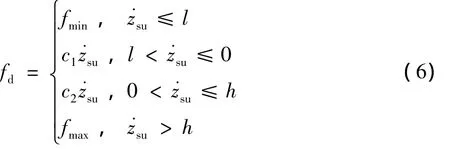
式中:c1和c2为线性段减振器阻尼;fmax、fmin、l和h为常数 (拐点)。

图3 减振器阻尼力与悬架相对速度的非线性特性Fig.3 Nonlinear characteristic between the damping force and the relative velocity of suspension
图4 为建立的天棚模型,该模型在簧载质量与理想固定端之间增加了阻尼器。天棚模型不考虑二自由度主动悬架模型的轮胎刚度和轮胎阻尼,其输入为二自由度主动悬架模型中非簧载质量的位移和速度。天棚模型中的簧载质量动力学方程为

式中:zsr为天棚模型的簧载质量位移;fsr、fdr和fsk分别为天棚模型中悬架弹簧力、减振器的阻尼力和天棚阻尼力。

图4 天棚模型Fig.4 Skyhook model
天棚模型不必是一个实际的系统,它可以是任何理想的数学模型。通常情况下,根据汽车平顺性和操纵稳定性的要求,确定天棚模型中的悬架刚度和减振器的阻尼。为了简化处理,本文天棚模型中的悬架刚度和减振器的阻尼分别等于二自由度主动悬架模型中线性段的悬架刚度 (k2)和减振器的阻尼(c2)。
2 基于参考模型和扰动观测器的滑模控制算法
在对悬架进行控制系统的设计时,路面激励未知,且模型具有非线性及不确定性,易受到外界的干扰。为了确保主动悬架控制系统的稳定性,建立的主动悬架的控制算法应具有较强的鲁棒性。滑模控制是一种变结构控制,适用于有扰动的线性系统或者非线性系统,对外部的干扰不敏感,具有较强的鲁棒性。
以降低簧载质量加速度为目标,同时保证悬架系统处在平衡位置时悬架动行程收敛于零,文中基于滑模控制算法设计了扰动观测器,估计了系统中的扰动,并设计控制力的表达式,证明了控制系统的一致有界和一致最终有界。
2.1 滑模控制器的设计
本文选择的滑模面是一个关于天棚模型和二自由度主动悬架模型的簧载质量位移及速度差值的线性组合函数[14-15],可以构造为

式中:v1和v2为滑模面的控制参数;e1和e2分别为二自由度主动悬架模型与天棚模型的簧载质量位移差值和速度差值;x为二自由度主动悬架模型中簧载质量位移和速度的向量。
若滑模面在有限的时间内收敛于零时,可得

求解式 (12),e1与e2的解为
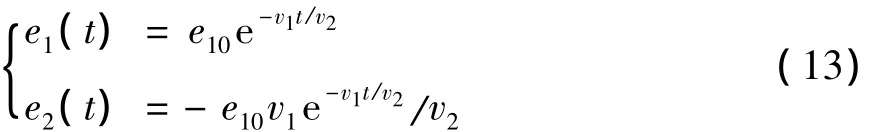
式中,e10为e1的初始值,t为时间。
由式 (13)可知,若控制参数v1与v2符号相同且 v1> v2,则e1、e2在有限的时间内都趋近于零,即二自由度主动悬架模型中簧载质量位移和速度分别等于天棚模型中簧载质量的位移和速度,从而降低了主动悬架系统中簧载质量的加速度,同时保证了悬架系统处在平衡位置时悬架动行程收敛于零。
为了满足式 (13),滑模面及其导数的乘积需要满足条件为

由式 (14)可知,通过构造滑模面的导数,使得滑模面在有限的时间内趋近于零。对式 (9)求导,滑模面的导数为

将式 (1)和式 (10)代入式 (15),可得
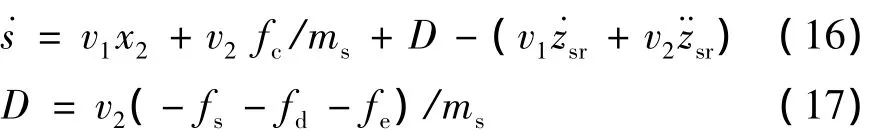
式中,D为非线性二自由度主动悬架系统中扰动量的总和。
根据式 (16),给出的控制力为

式中:fc为控制力;k为大于零的控制参数;^D为扰动观测器对非线性二自由度主动悬架中扰动量总和D的估计值。
将式 (19)、(20)代入式 (18),控制力为

将式 (21)代入式 (16),可得

2.2 扰动观测器的设计
假设1 扰动量总和D变化率的绝对值是有界限函数,即

其中θ为正数。
给出的扰动观测器的估计值为
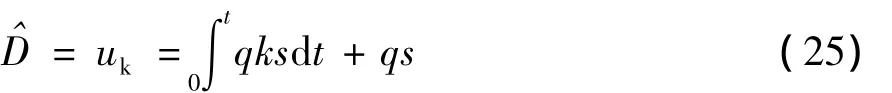
式中,q为大于零的控制参数。
将式 (25)代入式 (21),控制力的表达式为

定理1 对于满足假设1的扰动量,控制力(式 (26))能够保证主动悬架系统一致有界和一致最终有界,即扰动观察估计值的误差~D和滑模面s一致有界和一致最终有界。
定义1(一致有界) 描述系统中扰动观察估计值的误差~D,且~D(t0)=~D0。系统是一致有界的:若对于任意r>0,存在一个正常数d(r)<∞,使得对于所有的t>t0,都有


证明 选取的Lyapunov函数为

对上式求导可得

根据式 (23)和 (25),式 (30)可以写为
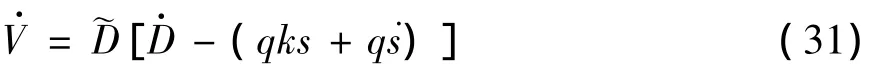
将式 (22)代入式 (31),可得

由式 (32)可知,扰动观察估计值的误差~D一致有界和一致最终有界为[16-17]

若选择的控制参数q为足够大的正数,R和d—可以收敛到零。由式 (22)可知,滑模面一致有界和一致最终有界。证毕。
注1 当系统中的扰动量满足假设1时,设计的控制力 (式 (26))可以使得扰动观察估计值的误差和滑模面均一致有界和一致最终有界。由式 (9)可知,主动悬架系统具有一致有界和一致最终有界;另外也证实了设计的扰动观测器 (式 (25))的有效性。
3 主动悬架系统的试验与仿真分析
3.1 实验设备与数据采集
为了验证主动悬架模型的正确性和具有扰动观测器的滑模控制算法对非线性二自由度主动悬架系统的有效性,利用Quanser-Active Suspension试验设备进行非线性二自由度悬架系统主动控制试验[18]。
试验设备中的二自由度悬架实物图和原理图如图5所示,主要由簧载质量、非簧载质量、悬架弹簧、轮胎弹簧和2个电机 (控制电机和驱动电机)组成。在簧载质量与非簧载质量之间,试验设备中没有安装阻尼装置,用运动过程中直线轴承与导轨之间的摩擦力模拟减振器的阻尼力;在簧载质量与非簧载质量之间的直线导轨上,安装了外径大且长度小于悬架弹簧的弹簧以模拟缓冲块的刚度;在簧载质量与其上端的固定端之间,安装了弹簧以模拟作用于簧载质量上的干扰力,如图5(b)所示。控制电机仅作为所设计的控制力的执行器。

图5 二自由度主动悬架的实物图和原理图Fig.5 Prototype diagram and schematic diagram of active suspension systems of two degrees of freedom
位于底部的驱动电机为伺服电机,产生路面激励位移;中部的控制电机为直流电机,产生控制力。通过安装在簧载质量上的加速度传感器测量簧载质量加速度;通过安装在簧载质量和控制电机上的转角编码器测量簧载质量位移和悬架相对位移。利用测量的簧载质量位移和悬架相对位移得到非簧载质量的位移。通过对测试的簧载质量和非簧载质量位移进行低通滤波求导,计算出簧载质量和非簧载质量的速度。本文选择的2阶低通滤波求导器为

式中:H为传递函数;E为拉普拉斯变量;ω为常数,文中ω取值为500。
3.2 控制参数的选择
在进行二自由度主动悬架试验时,其输入选择为典型的阶跃位移路面激励和随机路面激励。其中,阶跃位移zr1的表达式见式 (38),其图形见图6。

图6 阶跃位移的路面激励Fig.6 Road excitation of step displacement
由图6可见,激振频率成分主要在0~5 Hz之间。

随机路面激励的表达式为

式中:zr2为路面的垂向位移;车速j为50 km/h;路面不平度系Gzr(n0)为64×10-6m3;下截止频率f0为0.1Hz;w为数字期望为0的高斯白噪声。
二自由度主动悬架系统中,簧载质量ms和非簧载质量mu分别为2.45 kg和1.00 kg;轮胎刚度kt和阻尼ct分别为2500 N/m和5 N·s/m;悬架弹簧刚度k1和k2分别为900N/m和2443.2N/m,其拐点为-2.2mm;减振器阻尼c1和c2为20N·s/m;其拐点l和h分别为-0.15m/s和0.15m/s。
由式 (13)可知,控制参数v1和v2为符号相同且 v1> v2。控制参数k和q均为大于0的正常数。在满足上述要求的条件下,保证控制系统渐进稳定。然而,在工程上,通过考虑控制的成本、系统稳定的时间和作动器的饱和等问题,这些控制参数可以优化得到。由于本文主要研究滑模控制器的设计,因此控制参数是根据系统的稳定时间反复调整得到的。选择的控制参数如下:v1=4;v2=1;k=5;q=100。
3.3 非线性二自由度主动悬架模型的验证
在阶跃路面激励下,计算滑模控制的主动悬架系统的控制力 (式 (26))、簧载质量和非簧载质量位移;同时,利用主动悬架试验台和控制力,测试得到簧载质量和非簧载质量位移。
图7为主动悬架系统中簧载质量和非簧载质量位移的试验值和计算值。由图可知,簧载质量和非簧载质量位移的试验值和计算值相差较小,从而验证了非线性二自由度主动悬架模型的正确性。而图7中试验值和计算值的差异性,主要是由于减振器的阻尼系数不准确和试验台存在摩擦因素。

图7 簧载质量和非簧载质量位移的试验值和计算值Fig.7 Calculated and measured values of sprung mass displacement and unsprung mass displacement
3.4 滑模控制算法的有效性分析
在阶跃路面激励下,不考虑外界的干扰力,测试了采用本文的控制时主动悬架系统中的悬架动行程。根据测试的悬架动行程,利用式 (4)计算出悬架弹簧力。图8为主动悬架系统中的悬架动行程和悬架弹簧力。由图8(a)可知,当悬架系统处于平衡时,悬架动行程等于零。当悬架动行程小于式 (4)中的拐点a(-2.2 mm)时,悬架刚度值由第2段线性刚度k2变为第1段线性刚度k1,悬架弹簧力产生了突变,如图8(b)所示。

图8 悬架动行程和悬架弹簧力Fig.8 Suspension deflection and suspension spring force
测试了采用本文的控制和无控制时主动悬架模型中的簧载质量加速度,分别记为Ac:Control和Ac:No control。将测试得到的主动悬架系统中的非簧载质量位移和速度作为天棚模型的输入,计算了天棚模型中的簧载质量加速度 (Ac:RSM)。
图9为在阶跃路面激励或在随机路面激励下,采用本文的控制和无控制时主动悬架模型中的簧载质量加速度以及天棚模型中的簧载质量加速度。由图9(a)可见,在阶跃路面激励下,与无控制相比,采用本文的控制时主动悬架模型的簧载质量加速度偏小且主动悬架系统稳定时间更短。由图9(b)可见,在随机路面激励下,与无控制相比,采用本文的控制时主动悬架模型的簧载质量加速度偏小。因此,由图9可知,主动悬架模型的簧载质量加速度与天棚模型中的簧载质量加速度有较好的一致性。上述分析说明基于天棚模型和扰动观测器的滑模控制算法对主动悬架系统是有效的。

图9 在阶跃路面激励或随机路面激励下的簧载质量加速度Fig.9 Sprung mass acceleration under road excitation of step displacement or road excitation of random displacement
3.5 干扰力对主动悬架系统控制效果的影响
在阶跃路面激励下,为了分析基于天棚模型和扰动观测器的滑模控制算法的有效性,研究了干扰力对主动悬架系统的控制效果的影响。为了便于试验进行,在主动悬架试验台中簧载质量与其上端的固定板之间安装了弹簧以模拟干扰力,如图5(b)所示。干扰力的表达式为

式中,ke为簧载质量与其上端的固定板之间的弹簧刚度,其值为258.6N/m。由图7(a)可知,簧载质量的位移可以近似等于30mm。根据式 (40),最大的外界干扰力可以近似等于0.3 msg。实际工程中,外界的干扰力比较复杂且具有多种类型,本文选择的干扰力是为了便于试验的研究。
在阶跃路面激励下,试验测试得到有、无控制下的簧载质量加速度,如图10所示。在干扰力的作用下,与无控制相比,滑模控制主动悬架模型的簧载质量加速度偏小,滑模控制的主动悬架系统的稳定时间更短。由此表明:干扰力对滑模控制效果的影响较小,具有扰动观测器的悬架滑模控制算法具有良好的鲁棒性。

图10 簧载质量上有干扰力情况下有、无控制时簧载质量加速度的测试值Fig.10 Measured acceleration of sprung mass with and without control under external disturbance force
测试了主动悬架系统中簧载质量和非簧载质量的位移和速度,以及计算了天棚模型的簧载质量加速度,得到了在簧载质量有、无干扰力下主动悬架的控制力,如图11所示。由图可知,与无干扰相比,有干扰的控制力偏大。

图11 在簧载质量上有、无干扰力时主动悬架的控制力Fig.11 Control force acting on the sprung mass in active suspension systems with and without external disturbance force
4 主动悬架系统性能指标的计算分析
在阶跃路面激励下,基于非线性二自由度主动悬架模型,计算了线性二次型最优控制 (LQR)、具有扰动观测器的滑模控制 (DOSMC)和基于天棚模型和扰动观测器的滑模控制 (RMDOSMC)下主动悬架系统中簧载质量加速度、悬架动行程和轮胎动载荷的性能指标,以评价本文提出的滑模控制的主动悬架控制系统性能。
根据文献[19],LQR控制算法针对的是线性二自由度悬架模型,因此,忽略悬架弹簧力与悬架动行程的非线性特性。当使用LQR控制主动悬架系统时,将悬架刚度和减振器阻尼分别设置为k2和c2。与LQR控制相比,基于天棚模型和扰动观测器滑模控制下主动悬架系统可以获得更好的控制效果。为了验证上述结论,在阶跃路面激励下,不考虑外界的干扰力,对比分析了 LQR控制、DOSMC控制和RMDOSMC控制下主动悬架系统中簧载质量加速度 (¨zs)、悬架动行程 (zsu)和轮胎动载荷 (ft)的性能指标。
图12为LQR控制、DOSMC控制和RMDOSMC控制下二自由度主动悬架系统的性能指标。与LQR控制相比较,RMDOSMC控制下主动悬架系统中的簧载质量加速度和悬架动行程绝对值的最大值偏小,轮胎动载荷绝对值的最大值稍微偏大。


图12 LQR控制和滑模控制的主动悬架系统的性能指标Fig.12 Performance index of active suspension systems with LQR control and sliding mode control
与DOSMC控制相比,RMDOSMC控制下主动悬架系统中的簧载质量加速度绝对值的最大值稍微偏大,轮胎动载荷绝对值的最大值比较接近,但RMDOSMC控制下主动悬架系统中的悬架动行程绝对值的最大值偏小。在0.5 s以后悬架系统处在平衡位置时,DOSMC控制下主动悬架系统中悬架动行程不为零。主要原因为DOSMC控制下主动悬架系统中簧载质量的位移接近于零,然而非簧载质量位移等于路面激励振幅的最大值 (25 mm),这会使得悬架处于压缩状态。研究结果表明:对于非线性二自由度悬架系统,RMDOSMC控制下主动悬架系统可以获得更优的性能指标。
当汽车遇到上坡工况或者下坡工况时,坡度越高会使得DOSMC控制下的悬架动行程越大,出现悬架撞击车身和轮胎脱离地面的现象,严重影响汽车的平顺性和汽车零件的疲劳寿命。
5 结论
(1)试验证实了基于天棚模型和扰动观测器的滑模控制算法对非线性二自由度主动悬架系统的有效性。在阶跃路面和随机路面激励下,与无控制相比,滑模控制下簧载质量的加速度偏小;主动悬架模型的簧载质量加速度与天棚模型中的簧载质量加速度有较好的一致性。
(2)试验分析了外界的干扰对所设计的滑模控制下主动悬架系统控制效果的影响。在存在较大的外界干扰下,基于天棚模型和扰动观测器滑模控制下的主动悬架系统有较好的控制效果,所提出的滑模控制算法具有良好的鲁棒性。
(3)分析了LQR控制和滑模控制下簧载质量加速度、悬架动行程和轮胎动载荷的悬架性能指标。与LQR控制比较,基于天棚模型和扰动观测器滑模控制下的簧载质量加速度和悬架动行程绝对值的最大值偏小。与具有扰动观测器的滑模控制比较,基于天棚模型和扰动观测器滑模控制下的悬架动行程在有限的时间内收敛于零,不会出现悬架被击穿的现象。因此,基于天棚模型和扰动观测器滑模控制下的主动悬架可以获得更优的性能指标。

