RV传动机构用转臂轴承的受力及接触特性分析

吴素珍 何卫东 张迎辉

(1.大连交通大学机械工程学院，辽宁大连116028;2.河南工程学院机械工程学院，河南郑州451191)

RV传动是在摆线针轮传动基础上发展起来的一种新型传动，广泛应用于机器人、工程机械、能源及医疗、卫星接收系统等领域［1］。转臂轴承是RV传动机构中支撑传递扭矩的关键零部件，由于尺寸受限，通常由曲柄轴外圈和摆线轮内孔分别作轴承内圈和外圈，是RV减速器的薄弱环节。RV传动属于静不定系统，其受力分析十分复杂，既要满足静力平衡条件，又与有关弹性环节的变形协调条件有关，因此，如何准确获得曲柄转臂轴承的受力，进而分析转臂轴承的接触特性，是寻找延长其寿命的有效途径。

目前，国内外学者针对圆柱滚子轴承开展了一系列研究［2-7］，圆柱滚子轴承的受力分布及接触特性基本得到解决。Yang等［8］采用有限差分法(FDM)分析了四列圆柱滚子轴承在平滑状态下的弹性流体动力润滑特性，总结出不同表面粗糙度条件下，四列圆柱滚子轴承的载荷和压力分布;Liu等［9］创新地提出了一种分析动力学模型，分析在离心力和外部载荷作用下滚子变形、滚道变形、外部载荷和转速对圆柱滚子轴承振动特性的影响;刘延斌等［10］基于牛顿-欧拉动力学及接触力学理论，建立了轴承的动力学模型，分析了兜孔的弧面偏置角、弧面半径对滚子打滑和保持架涡动的影响规律。RV传动机构用转臂轴承为无内、外圈的圆柱滚子轴承，对于RV传动机构的特殊性，要准确分析不同工况下转臂轴承的受力及接触性能，存在较大难度。由于国外的技术封锁，了解该方面的新技术研究十分有限。姚文席等［11］采用解析法分析了RV传动机构中转臂轴承的载荷分布，得到该轴承即使承受恒定负载，也受有动载荷;张振强等［12］从RV减速器的运动原理和结构特点出发，采用理论力学法分析了RV减速器中转臂轴承、曲轴支撑轴承和圆锥滚子轴承的受力状况，结果表明主轴承受力最大，转臂轴承次之，圆锥滚子轴承受力最小;何卫东等［13］考虑摆线轮体变形及滚动轴承初始径向间隙等因素，运用有限元法分析了摆线轮和曲柄轴承的应力分布规律，得到由于摆线轮结构分布不均，产生结构大变形，进而导致啮合齿存在不连续现象;Li等［14］建立了滚子轴承受力分析模型和刚度矩阵计算模型，计算了曲柄轴承的时变轴承刚度，得出修形、转矩和偏心距对扭转啮合刚度、承载传动误差和载荷分布因子具有重要影响。

综上所述，针对RV减速器用转臂轴承的受力分析和接触特性分析，现有研究未考虑或仅考虑了部分部件变形及各部件相互作用间的影响。为更精准计算转臂轴承受力，本文考虑修形、弹性变形、间隙、摩擦等多个因素，以及摆线轮、针轮、中心轮、3个行星轮、3个曲柄轴、3个转臂轴承等多传动部件间相互耦合在传动系统中的传播特性，同时考虑摆线针轮和中心轮行星轮的接触非线性以及摆线针轮传动受力的时变性，构建了考虑非线性和时变性的多因素、多部件RV传动机构整机系统多体动力学模型。利用该模型分析不同转速和负载工况下转臂轴承受力特性;同时采用解析法计算其受力，并将解析法与多体动力学法对比。文中还在转臂轴承受力特性分析的基础上，进一步建立含有曲柄轴、滚子和摆线轮的有限元模型，分析不同负载工况下RV转臂轴承的接触应力特性，研究负载对转臂轴承疲劳寿命的影响。

1 传动机构的相关参数

RV传动机构属于曲柄式封闭差动轮系，是由渐开线传动和摆线针轮传动组成的两级新型传动机构，其基本技术参数如表1所示。该RV减速器额定转矩为784 N·m，额定输出转速为15 r/min，能承受的最大转矩为2.5倍额定转矩，在外壳转动时，转速比为120。用来支撑摆线轮的转臂轴承基本设计参数如表2所示。

2 解析法计算转臂轴承受力分析模型

根据RV传动机构的工作原理可知，转臂轴承对摆线轮的作用力，与针齿摆线轮啮合的作用力及输出机构对摆线轮的作用力相平衡。

表1 RV-80E减速器基本技术参数Table 1 Basic technical parameters of RV-80E reducer

表2 转臂轴承基本设计参数Table 2 Basic design parameters of rotary arm bearing

2.1 针齿对摆线轮的作用力合力

针齿作用在摆线轮上的力都通过节点D，现将各啮合点中的作用力沿作用线移到节点D，并分解成沿X轴的分力P1x，P2x，…和沿Y轴的分力P1y，P2y，…，如图1所示。各作用力在X轴方向的分力和∑Px为［15-17］

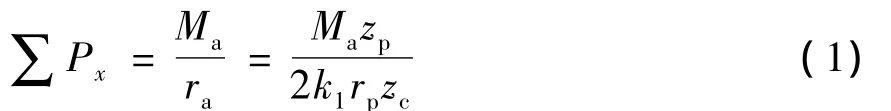
式中:Ma为RV机构承受的负载;ra为摆线轮理论齿廓的平均半径;zp为针齿齿数;k1为短幅系数;rp为针轮中心圆半径;zc为摆线轮齿数。

各作用力在Y轴方向的分力和∑Py为

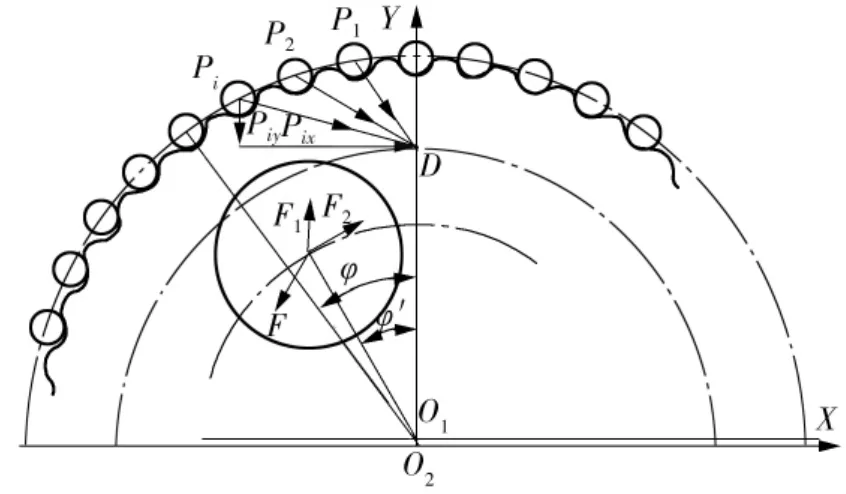
图1 转臂轴承受力分析Fig.1 Analysis of rotary arm bearing force

式中:i为针齿号，i=1，2，…，zp/2;φ为针轮绕其中心的转角，φ=ω2t(ω2为针轮的旋转角速度，t为旋转时间);φ′为摆线轮的转角，

2.2 输出机构对摆线轮的合力

RV传动机构中有n个曲轴且呈圆周均布，曲轴上的每个转臂轴承对摆线轮的力都可以分解为两个分量F1和F2，其中F1=-F/n，其对摆线轮中心的合力矩为零，F2表示轴承为摆线轮提供扭矩的力，F2的方向垂直于摆线轮的半径，其合力为零，对摆线轮的合力矩为M，F的大小为F=a22Ma/［nm(z1+z2)］，其中m为中心齿轮、行星齿轮的模数。

2.3 转臂轴承的受力

根据作用力的平衡条件，转臂轴承的受力大小F为

式中，Fx、Fy分别为转臂轴承在X方向、Y方向的受力。

编制Matlab程序，计算转臂轴承于极限工况下在X方向、Y方向的分力及合力大小，结果如图2所示。从图2可看出，当曲柄轴旋转一周时，转臂轴承受力F呈现一定周期性的波动力，合力F最大值为12134N，最小值为948.52N。

图2 转臂轴承受力结果Fig.2 Rotary arm bearing force result

3 基于多体动力学的转臂轴承受力分析

3.1 建立RV传动机构整机多体动力学模型

考虑各传动部件间的相互耦合，在广义坐标系OXY下，构建了含有第1级中心轮、3个行星轮，第2级摆线轮、针轮、针齿壳、3个曲柄轴、左右行星架等多部件的RV减速器整机系统多体动力学模型。在模型中，输入轴轴线方向与X方向一致，Y、Z方向与摆线轮平面的水平方向和竖直方向一致。根据精密摆线减速器各部件的材料属性，定义各部件材料属性。材料类型定义为steel，其密度设定为7801kg/m3，杨氏模量为2.07×109N/m2，泊松比为0.29。

为准确计算多个部件间的相互耦合，同时减小3D模型误差的影响，RV减速器多体动力学模型中各部件间的约束分配设置如表3所示。此外，中心轮与行星轮齿轮副、摆线轮与针轮齿轮副间的接触不做假设和简化，接触状态由多体动力学模型自行判断，转臂轴承、曲柄支撑轴承、主轴承采用旋转副模拟。

表3 RV减速器仿真模型的约束分配Table 3 Constrained allocation of RV simulation model

3.2 转臂轴承动力学分析

由于紧急停止或外部冲击，载荷瞬时剧增，出现最大工作载荷为2.5倍的额定载荷，从而给RV传动装置施加较大的转矩，造成RV传动装置转臂轴承破坏。为了解RV传动装置处于不同负荷下的轴承受力情况，本文对额定转速下的额定负载、极限负载和轻载工况下的轴承受力进行了动力学分析，分析工况如表4、5所示。

对工况1进行仿真分析，固定支撑法兰，在外壳旋转反方向上加载784×2.5N·m的转矩，在输入轴上加载额定转速15×120r/min，工况1转臂轴承的受力结果如图3所示。

表4 极限载荷、不同输入转速工况表Table 4 Working conditions at different input speeds with ultimate load

表5 额定转速、不同载荷工况表Table 5 Working conditions under different loads with rated speed

从图3的动力学分析结果可以看出，摆线轮上的转臂轴承1在Y向和Z向分别承受周期性正弦载荷，Y向最大值为12295 N，Z向最大值为9421 N。Y、Z方向受力分别为转臂轴承所受的径向、切向方向的力，X方向受力为零，说明转臂轴承不受轴向方向的力。

同一摆线轮均布有3个转臂轴承，工况1下3个转臂轴承的受力仿真结果如图4所示，从图4得出，同一摆线轮上的3个转臂轴承受力大小和周期性一致，相位差为120°。

极限载荷情况下，不同输入转速下的转臂轴承受力分析结果如图5所示。从图5的动力学分析结果来看，在相同负载、不同输入转速情况下，轴承受力的极值无影响，但是转速越快，轴承在相同时间内承受的交变载荷次数越多，会相应影响其疲劳寿命。

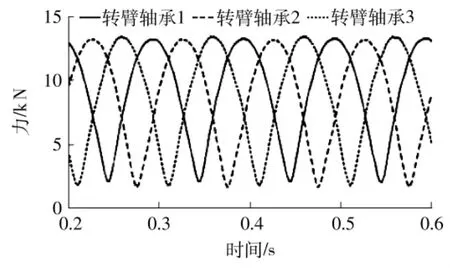
图4 工况1下同一摆线轮的3个转臂轴承受力Fig.4 Bearing forces of three rotary arms of the same cycloidal force under the first working condition

图5 工况1、2、3下的转臂轴承受力Fig.5 Bearing force of rotary arm under working conditions 1，2 and 3

额定输入转速时，额定负载、极限负载及轻载工况下转臂轴承的受力如图6所示。从动力学分析结果可看出，转速相同、负载不同情况下，轴承承受载荷各异，转臂轴承受力大小随施加负载的增加倍数成倍增长。极限工况下，转臂轴承受力最大值为13244.5N;额定工况、轻载工况下的最大值分别为5284.4N、2143.5N。

图6 工况4、5、6下的转臂轴承受力Fig.6 Bearing force of rotary arm under working conditions 4，5，and 6

3.3 转臂轴承受力结果对比

采用解析法和多体动力学法计算了2.5倍额定输出转矩工况下的转臂轴承受力，计算结果对比如图7所示。

图7 转臂轴承受力结果对比Fig.7 Comparison of bearing force of the rotary arm

由图7可知，极限工况下，多体动力学法计算出的轴承受力最大值为13 244.5 N，最小值为2031.5N，变化周期为0.1s;解析法计算出的转臂轴承受力最大值为12134.0 N，最小值为948.5 N，变化周期为0.1 s。两种方法得到的转臂轴承受力最大值、最小值不同，总体来说，两种方法得到的转臂轴承受力规律一致，均呈一定周期性波动，而多体动力学计算出的转臂轴承受力偏大，原因为多体动力学考虑了摆线轮、针轮、曲柄轴、转臂轴承、针齿、针齿壳等各部件与部件间的相互耦合作用。

4 转臂轴承的接触特性分析

4.1 有限元模型的建立

从上面的动力学分析可知，RV传动机构中圆周均布的3个曲轴上的每个转臂轴承受力大小和周期性是一致的。为此，在不影响计算结果的基础上，考虑到计算时间成本和结果精度问题，建立如图8所示模型，包括摆线轮、曲轴与轴承滚针。因保持架对轴承径向影响微弱，模型中未考虑保持架。为减小网格单元过大而造成的接触面穿透现象，设置模型滚针单元尺寸为0.2 mm、摆线轮与滚针的接触面单元尺寸为0.2mm、其他为1.0mm，本模型共形成1789408个节点、1397850个单元。曲轴、摆线论、滚针材料分别为18CrNiMnMoA、20CrMo和GCr15，即定义的曲轴、摆线论、滚针材料弹性模量分别为:2.12×1011、2.19×1011、2.1×1011Pa，密度分别为7860、7830、7850kg/m3，泊松比均为0.3。

图8 转臂轴承有限元模型Fig.8 Finite element model of rotary arm bearing

4.2 约束和加载

根据实际工况，转臂轴承在RV减速器中的受力情况为:偏心轴中心线承受载荷，然后通过轴承滚柱传递到摆线轮的轴承孔内表面，驱动摆线轮转动。在设置边界条件时，考虑了转臂轴承的具体结构、受力情况，并尽量与实际使用状态相一致。偏心轴外圈是轴承内圈，摆线轮内孔是轴承外圈，在各个啮合位置上轴承的载荷和受力方向都是变化的，而在固定外壳的情况下，摆线轮只在平面上做摆线运动，不存在转动现象，在每个时间点上摆线轮可看作是固定的，故在有限元分析边界条件中，固定摆线轮1、2、3三个方向的自由度，释放滚针在径向方向的自由度，固定其他方向的自由度。在截取的曲轴中心加载Y向和Z向在一个周期内的载荷。选取0.2s至0.3s之间的周期载荷，加载载荷为前面动力学分析中图6的结果。

4.3 接触特性分析

由上面的转臂受力分析可知，转臂轴承受力是具有一定周期性的波动力，即不同时刻转臂轴承受力不同。为分析转臂轴承运转一个周期内的接触应力分布情况，分析了转臂轴承工作一个周期内旋转到6个不同位置的接触强度分析模型，选取的几个时间点 (t)分别为 0.21、0.23、0.25、0.27、0.29、0.30s。图9所示为极限载荷工况下，转臂轴承一个周期载荷下不同时刻的应力、应变云图。

从图9的分析可知，在固定法兰盘、外壳转动的情况下，各时间点上各滚针应力各异，其主要应力分布在轴承左上方，存在单边受力的现象，排除t=0.30s上应力云图上的一些应力奇异点，其最大应力出现在t=0.29s时，最大应力为945.6MPa。

为模拟实际使用时的应力状态，分析额定载荷、极限载荷、轻载3种负载工况下，轴承各部件的应力、应变。在输出端加载，加载载荷为1个周期内的最大载荷，转臂轴承外圈、滚针和内圈的应力、应变规律如图10所示。

图9 一个周期内转臂轴承的应力云图Fig.9 Stress cloud diagrams of a slewing bearing in one cycle

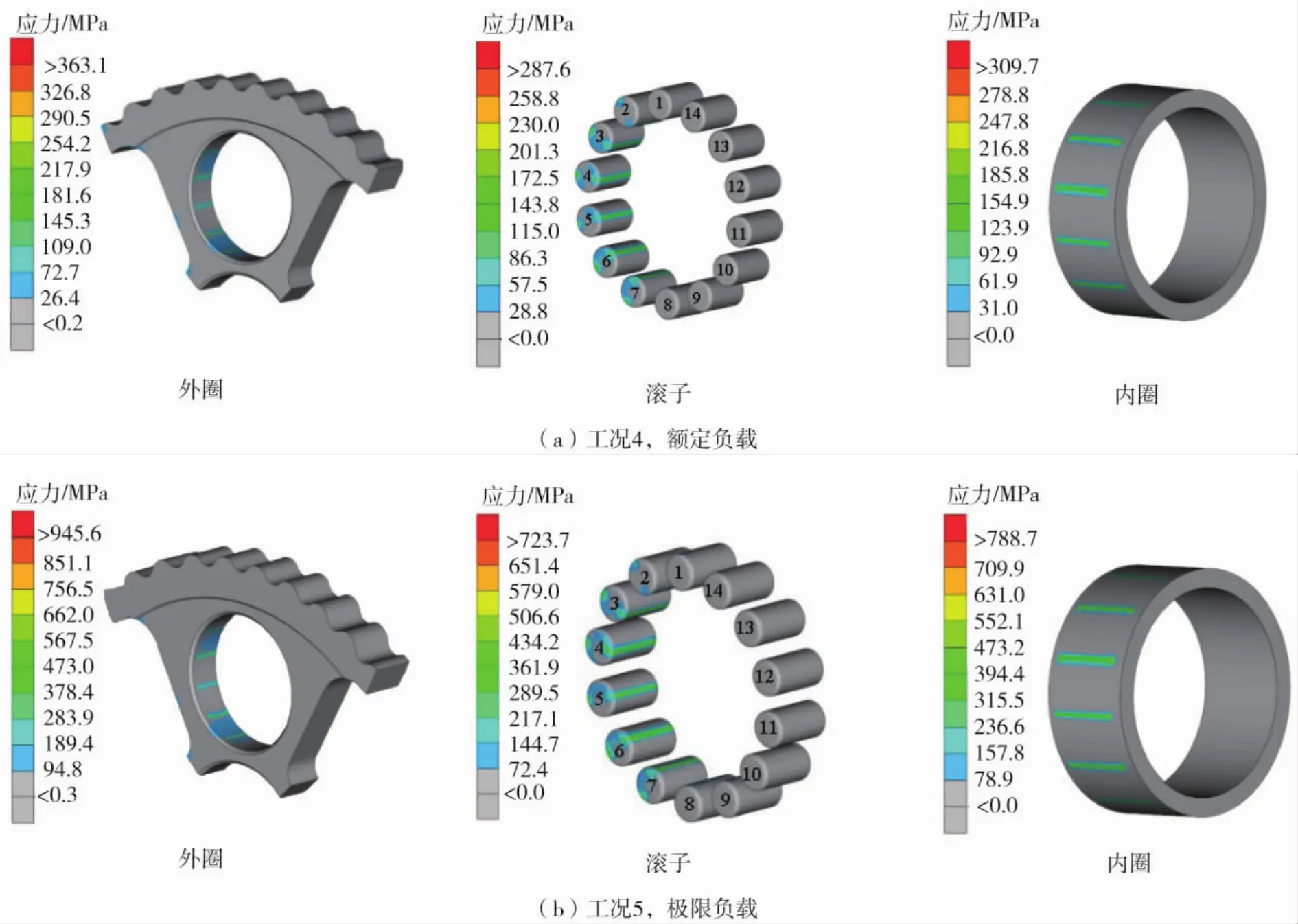
图10 3种负载工况下轴承各部件的应力云图Fig.10 Stress cloud diagrams of the bearing components under three load conditions

从图10可得出，在不同负载工况下，轴承应力大小不同，但其大小在材料的线性区域内的接触应力最大值与所受载荷呈线性关系，应力分布云图类似。在额定载荷下，摆线轮内圈最大接触应力为363.1MPa，轴承滚针的为287.6MPa，曲轴外圈接触面最大应力为309.7 MPa。在极限载荷下，摆线轮内圈最大接触应力为945.6 MPa，轴承滚针的为723.7 MPa，曲轴外圈接触面最大应力为788.7MPa。在轻载载荷下，摆线轮内圈最大接触应力为139.7MPa，轴承滚针的为109.2MPa，曲轴外圈接触面最大应力为116.4MPa。

图11为不同时刻各滚针与摆线轮内圈接触中心点的应力。从图11的接触应力可以得出转臂轴承的14个滚针应力各异，应力主要存在滚针1、2、3、4、5、6、7、14上面，其中滚针5上的应力最大，最大值为453.5 MPa，其余方向的滚针应力较小。

图11 滚子和摆线轮接触区域中心点应力曲线Fig.11 Center point stress curve of contact area between roller and cycloidal wheel

5 结论

(1)基于多体动力学，提出一种可精确计算转臂轴承的受力分析方法，并运用该方法进行实例分析，得到曲轴转臂轴承的受力呈周期性变化，并且动力学仿真结果与解析法计算吻合良好，从而验证了仿真模型的合理性。

(2)通过动力学模型分析可得，RV传动机构的输入转速对转臂轴承受力幅值无影响，但输入转速越高，转臂轴承在相同时间内承受的交变载荷次数越多，进而影响其疲劳寿命;RV传动承受的负载大小不同使转臂轴承承受的载荷各异，并且转臂轴承受力最大值随施加负载的增加倍数而增加。

(3)通过有限元法分析不同负载工况下转臂轴承接触应力、应变，结果发现:承受载荷越大，转臂轴承接触应力越大，轴承接触应力最大值增加量与载荷增加量近似线性关系;并且各时间点上各滚针应力各异，存在单边接触受力现象。