隧道监控量测数据反分析技术研究

侯光辉

（山西路桥第六工程有限公司，山西 晋中 030600）

1 隧道监控量测数据反分析研究现状

隧道监控量测数据反分析是根据隧道围岩位移监测数据的变化来反算岩体初始应力场及力学参数。1976年由Kirsten提出[1]，并先后在日本、意大利等国家得到推广与发展；国内1979年杨志法等学者首先提出了应用三维有限元图谱法进行位移反分析的计算方法，得到了国际专家的认可[2]；并于1985年通过建立流变模型进行了黏弹性反分析，此后多名学者投入研究并取得了很多成果；近年来，国内学者通过收集隧道监控量测资料建立BP网络模型[3]，对弹性模量E和侧压力系数K0进行验算，进一步分析隧道在初期支护后、仰拱开挖后、仰拱回填后、二次衬砌施作后等施工阶段的位移变化情况，并与监控量测实测数据对比分析，验证位移反分析计算数据的准确性，结果表明计算结果与现场隧道变形情况一致。通过位移反分析方法建模计算隧道围岩和支护结构的变形情况，预测变形规律，可为隧道支护结构的设计提供参考依据，合理确定隧道施工安全距离和支护参数。

2 工程概况

某公路隧道进口里程为K219+291，出口里程为K219+719，隧道全长436 m。隧道位于黄土高原干湿过度区，最大埋深159 m。穿越南东向展布的脊状山梁，为越岭隧道，两端为沟谷。地面高程1 154 m，相对高差约162 m，自然坡度20°～45°，地表植被发育。隧道出口段与当地乡镇道路相通，交通便利。隧道围岩主要为Ⅴ级围岩，局部分布有Ⅳ级围岩。隧道洞口段覆盖层厚度为2～5 m，围岩主要为砂岩，节理裂隙发育，岩体较破碎，稳定性差。隧道内不良地质主要有危岩落石、岩溶、松软土等，隧道施工中可能会遇到突水、突泥、塌方等地质灾害。隧道所在区域地表径流量较小，雨季水量大，地下水类型主要为裂隙水。隧道围岩结构稳定性差，在施工中布置测点进行监控量测，对地表下沉、拱顶下沉、周边位移收敛量测数据进行监测。

3 隧道监控量测数据位移反分析计算

3.1 隧道模型的建立

依托某在建公路隧道工程，采用MIDAS GTS软件建立三维模型[4]，对K219+320—K219+400施工段进行模拟。模型中通过有限元对初期支护、仰拱开挖和填充施工、二衬施工等施工阶段隧道变形情况进行了模拟。该段隧道属深埋区，覆盖层厚度在70～75 m。选取断面中心桩号K219+360，模型以隧道中线为基准，左右方向和上下方向各延伸40 m。由于隧道埋深大，且隧道内围岩分布均匀，模型中忽略了地形地貌，将隧道原地面当作平面进行模拟[5]。隧道模型特性参数如表1所示。

通过在模型中添加边界条件和荷载，模拟各个施工阶段，使用MIDAS GTS软件分析后得出不同施工阶段隧道各部分的变形和受力情况，图1为隧道整体竖向变形位移模拟。

表1 隧道模型特性参数统计表

图1 隧道整体竖向变形位移模拟图

3.2 位移反分析的计算方法

模型建立过程中，固定参数选择隧道的围岩参数，待定参数为弹性模量E和侧压力系数K0，需要通过反分析计算确定[6]。为完成对待定参数计算，进行以下假定：

a）假定G（x）为隧道变形函数，则隧道变形方程为：G（x）=G（E，K0），G（E，K0）可以通过数值模拟计算得出。

b）隧道施工过程中的实际变形量为D，为隧道各施工阶段实测值，假定构造函数：f（x）=│G（E，K0）-D│。

c）当f（x）取最小值时，此时（E，K0）为最优解。

3.2.1 弹性模量E的计算步骤

对弹性模量E和侧压力系数K0应用多参数的黄金分割法进行分析，计算得出取值范围，进行模型分析后确定最终值。弹性模量E计算步骤如下：

a）根据黄金分割法，取侧压力系数K0=0.5，将弹性模量E的取值区间确定为（2.0，6.0），取黄金分割系数α=0.618，根据黄金分割计算公式计算确定c=4.486，d=3.544，将 c，d 代入模型。

b）当E=4.486时，拱顶最终沉降量DZ=19.40 mm，计算变量：

c）当E=3.544时，拱顶最终沉降量DZ=19.40 mm，计算变量：

d）根据上述计算结果，得出f（4.486）＜f（3.544），重新划分分割区域，取a1=3.544，b1=6.0，c1=5.058，d1=4.486。将E=5.050代入模型进一步计算最终沉降量。计算变量：

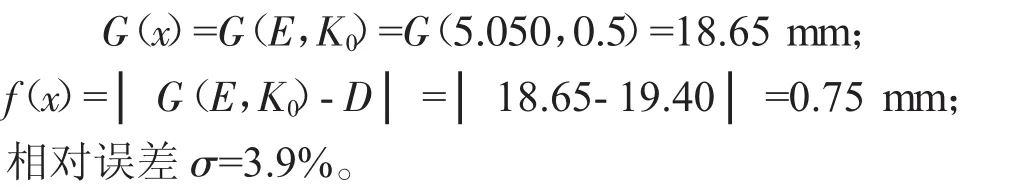
e）由于f（5.050）＜f（4.486），重新划分分割区域，得出c2=5.436，取E=5.436，计算得出最终相对误差σ=10.32%。

f）以同样的方法进行计算，最终得出当E=4.846时求得的绝对误差 σ=0.49%，f（4.846）=0.11 mm＜1 mm；当E=5.058时，f（5.058）=0.75 mm＜1 mm。因此，得出弹性模量E的取值范围为（4.846，5.058）。

采取同样的计算方法，确定侧压力系数K0的取值范围为（0.931，0.973）。在这两个值的取值范围内将不同的取值进行模型分析，并结合实测结果，最终确定 E=4.952 GPa，K0=0.955。

4 位移反分析结果对比分析

为了确定模型计算数据的准确性，在K219+340—K219+400段选取K219+360断面对隧道拱顶下沉和净空位移进行量测，并将位移反分析计算结果与实测结果进行对比分析，如表2所示。

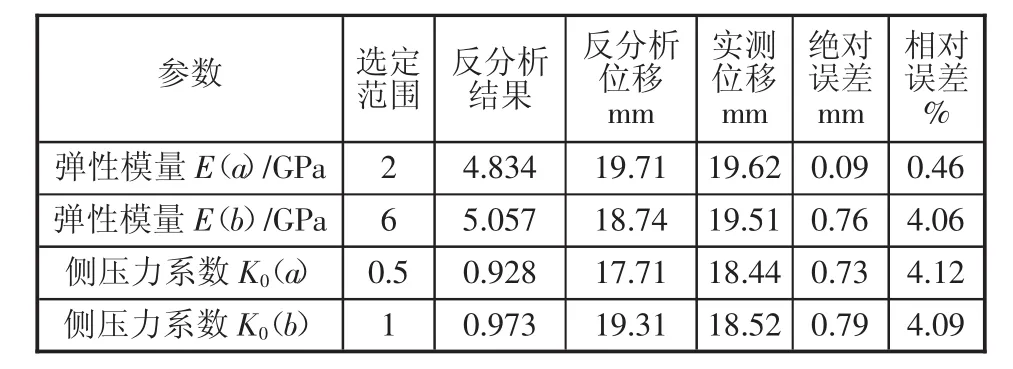
表2 K219+360断面反分析结果统计表

通过对表2结果分析，得出采用软件建模反分析计算所得出的位移计算值与实测位移值相差较小，其中绝对误差最大值为0.79 mm，相对误差最大值为4.12%，均在允许范围内，说明模型计算数据的准确性符合要求。

通过反分析计算，确定E=4.952 GPa，K0=0.955，将该值代入MIDAS模型中，在隧道K219+360断面开挖、初期支护、仰拱开挖和填充施工、二衬施工等施工过程中进行模拟计算，对拱顶下沉和净空位移变形情况进行位移反分析，得出各阶段隧道反分析结果如图2～图5所示，本文只对隧道初期支护和仰拱开挖阶段的分析结果进行分析。

图2 初期支护后K219+360断面拱顶沉降模型图

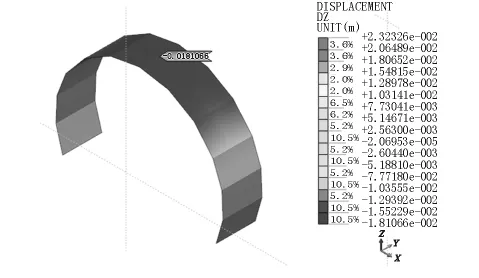
图3 仰拱开挖后K219+360断面拱顶沉降模型图

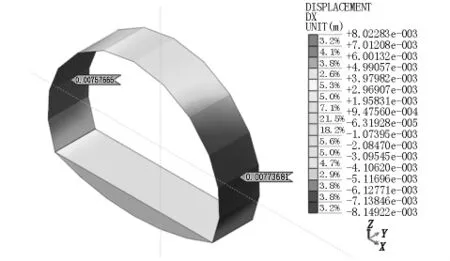
图4 仰拱填充K219+360断面水平位移模型图

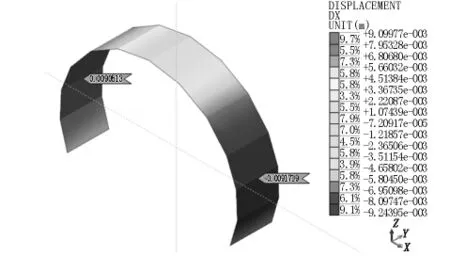
图5二衬施工K219+360断面水平位移模型图

根据模型中给出的K219+360断面初期支护后、仰拱开挖后的位移反分析结果，结合隧道仰拱填充后、二次衬砌施工后的计算结果，对断面拱顶下沉和净空位移变形情况的模型计算结果和实测值进行对比分析，如表3所示。

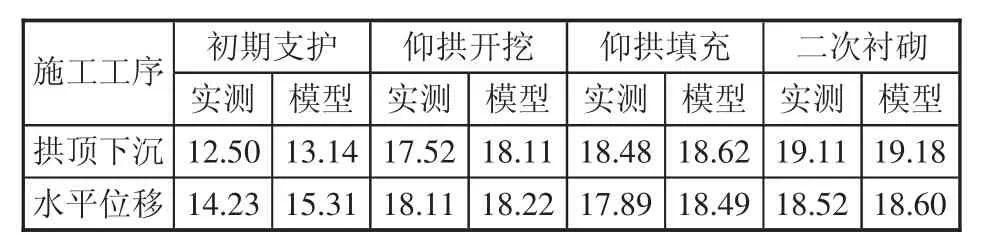
表3 K219+360断面位移变形对比表 mm

根据表3数据，绘制各施工工序拱顶下沉和净空位移实测值与模型计算值变化曲线，如图6和图7所示，图中1、2、3、4分别代表初期支护、仰拱开挖、仰拱回填、二次衬砌4个施工工序。

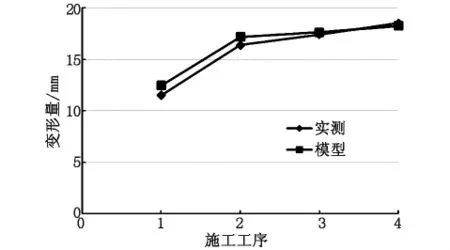
图6 拱顶下沉实测值与模型计算值变化曲线

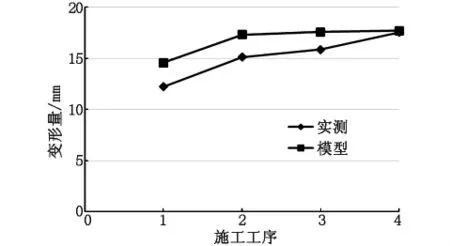
图7 净空位移实测值与模型计算值变化曲线

通过对表3数据和图6、图7曲线进行分析，得出反分析计算结果可以与实测数据相符合，数据相差较小，曲线变化趋势基本相同。应用同样的方法对其他断面量测数据进行反分析计算，分析后得出了相似的结论，说明应用模型对隧道各施工阶段的变形量测反分析计算结果准确可靠。

5 结语

结合在建隧道工程，采用MIDAS GTS软件对K219+340—K219+400段建立三维模型，对初期支护、仰拱开挖和填充施工、二衬施工等施工工序隧道变形情况进行模拟，并应用黄金分割法对隧道位移量测值进行了反分析计算，与实测值对比分析后得出以下结论：

a）建立有限元模型，应用黄金分割法，通过反分析计算得出弹性模量E的取值范围为（4.846，5.058），侧压力系数 K0的取值范围为（0.931，0.973）。

b）通过对比分析K219+360断面初期支护后、仰拱开挖后、仰拱填充后、二次衬砌施工后拱顶下沉的反分析计算结果，得出反分析计算结果可以与实测数据相符合，数据相差较小，曲线变化趋势基本相同，说明对拱顶下沉和水平位移反分析计算结果准确可靠。