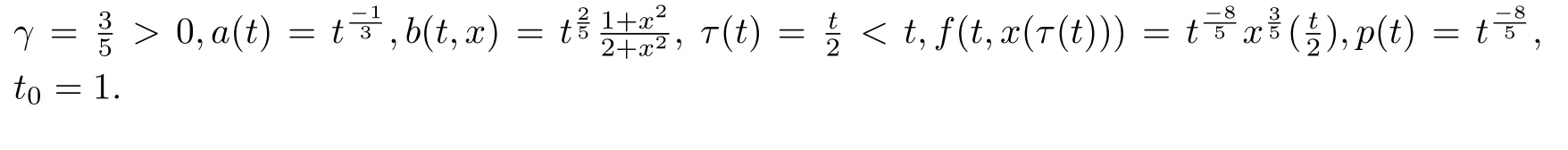时标上三阶非线性时滞动力方程的振动性定理

冯瑞华, 仉志余

(1.中北大学理学院,山西太原030051;2.太原工业学院理学系,山西太原030008)

§1 引 言

1988年德国学者Stenfan Hilger在其博士论文中首次提出了测度链分析理论,既适合连续系统也适应于离散系统,把微分方程和差分方程理论和方法统一了起来.但起初关注的学者并不多,后来随着时标上微积分知识的积累,人们发现时标上动力方程在理论物理,核动力学,物理化学,电子工程和经济学领域有着广泛的应用前景,例如可以用来描述电路中电流的改变率,经济学中的蜘蛛网模型等.于是近年来涌现出了大量的研究成果,研究范围也不断拓宽,如时标上动力方程的振动性、渐近性的判定定理等,见文献[1-17]及其引文.

本文研究时标T上三阶非线性时滞动力方程

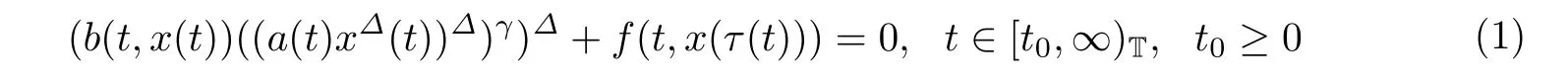
的振动性,并假设以下条件始终成立.

(H1)γ>0是两个正奇数之比的常数.

(H2)正值函数a(t)∈Crd(T,(0,∞))满足

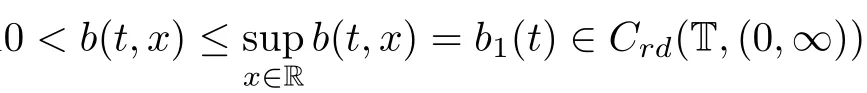
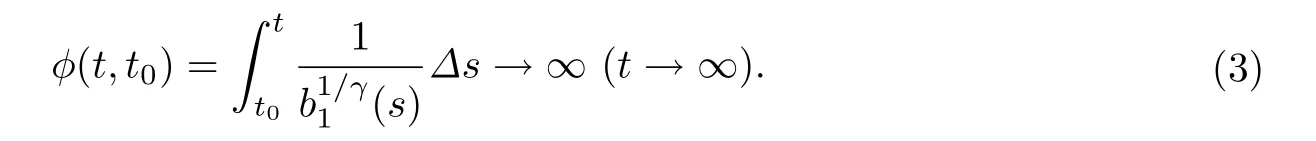
(H3)时滞函数τ:T→T单调增,且τ(t)≤t,limτ(t)=∞.

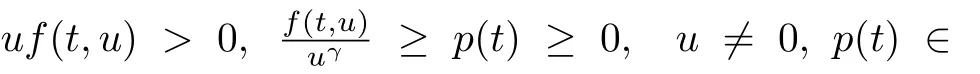
关于时标(或时间尺度)T及其上的微积分基本概念,性质,运算法则和记号可参见文献[8,9]等,这里不再重述.方程(1)的解是指定义在时间尺度T上满足方程(1)的非平凡实值函数x(t),t∈T.因为这里研究方程的振动性,所以假设时间尺度T是无界的.方程(1)的解x(t)称为振动的,如果既不最终为正,也不最终为负;否则,称为非振动的.方程(1)称为振动的,如果它的所有解都是振动的.

近年来对于三阶动力方程的振动性和渐进性的研究日趋活跃,并涌现出了不少具有启发意义的成果,例如:

当a(t)=1,b(t,x(t))=b(t)时方程(1)可以化为三阶非线性动力方程

或者

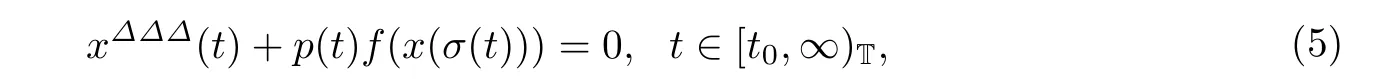
2007年Erbe等[1]研究了方程(4)的Hille和Nehari型振动准则,2017年魏会贤等[12]研究了方程(4)的变形方程(5)的渐进性态.

当a(t)=1,b(t,x(t))=b(t)时方程(1)可以化为三阶非线性动力方程

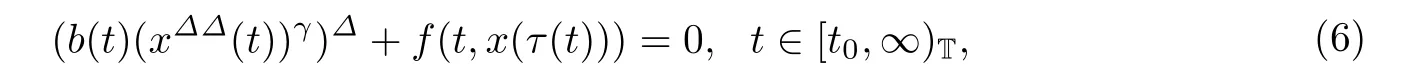
或者拓展为中立型的

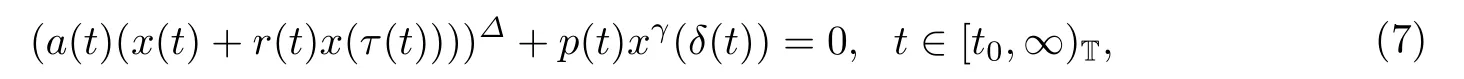
2011年李同兴等[4]研究了当f(t,x(τ(t))=p(t)xγ(τ(t))时方程(6)的振动性,给出了两个有效的振动定理.2017年王一拙等[14]研究了方程(7)的振动性.

当γ=1,τ(t)=t,b(t,x(t))=b(t)时方程(1)可以化为三阶非线性动力方程

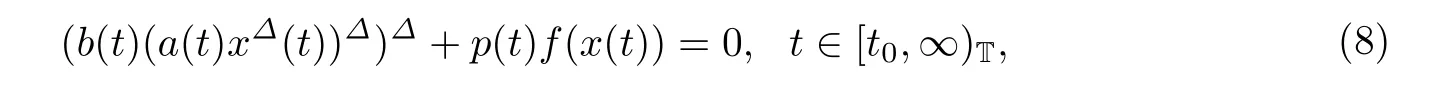
或者

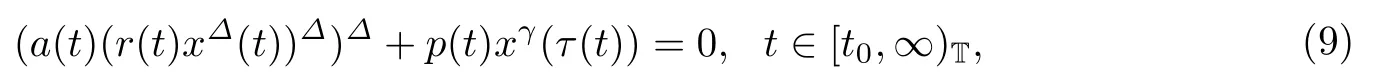
2005年Erbe等[2]建立了方程(8)的振动准则.2012年李同兴等[15]对方程的特形方程(9)的振动性给出了更精妙的结果.

当b(t,x(t))=b(t)时方程(1)可以化为三阶非线性动力方程

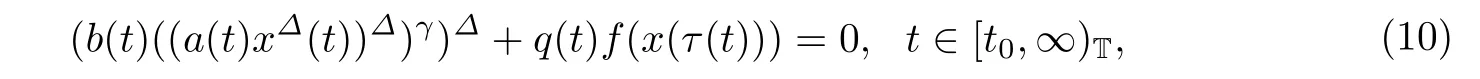
或者拓展为中立型的

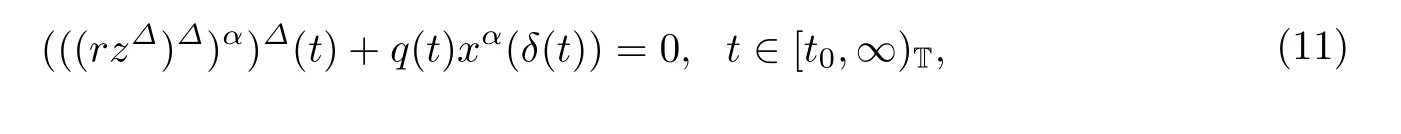
其中z(t)=x(t)+p(t)x(τ(t)).李同兴,Hassan和高丽等[3,5-8]分别研究了方程(10)在不同条件下的振动性,Candan和石云龙等[13,16]分别建立了中立型方程(11)的振动准则.

本文将运用不同于上述文献的Riccati变换和不等式技巧,得到方程(1)几个新的Leighton型,Philos型和Kamenev型振动定理,从而推广和丰富已有文献中的结果.

§2 基本引理

为了证明主要结论,需要用到下面的Keller链锁规则公式[9]:

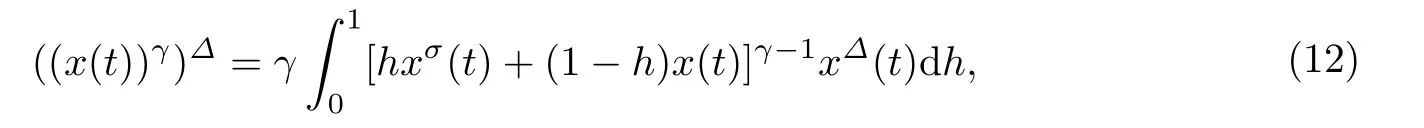
其中x(t)是∆可微的,γ>0,xσ=x◦σ.

下面给出几个引理,它们将对主要结果的证明起到至关重要的作用.

引理2.1设x(t)是方程(1)的一个最终正解,则存在t1∈[t0,∞)T,使得当t∈[t1,∞)T时,有且仅有下列两种情形之一:

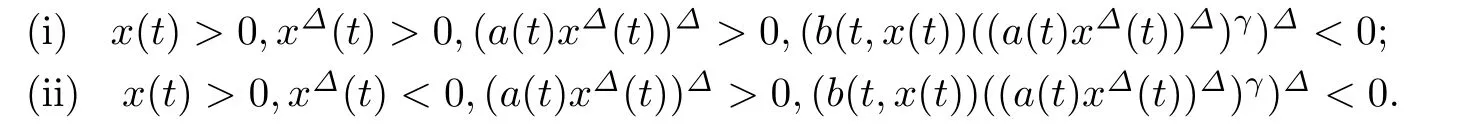
引理2.2设x(t)是方程(1)的一个最终正解并满足引理2.1中的情形(i),又设a∆(t)6 0和

成立,则存在t1∈[t0,∞)T,使得当t∈[t1,∞)T时,有严格单调减.

证设x(t)是方程(1)的一个最终正解并满足引理2.1中的情形(i).由于(a(t)x∆(t))∆=a∆(t)x∆(t)+a(σ(t))x∆∆(t)>0,并且有a∆(t)≤0和x∆(t)>0,t∈[t1,∞)T,因此可得x∆∆(t)>0,t∈[t1,∞)T.令X(t)=x(t)−tx∆(t),则有

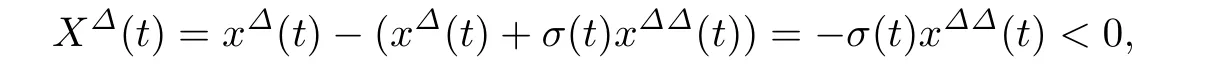
可知X(t)在[t1,∞)上是严格单调减的.可以断言,存在t2∈[t1,∞)T,当t∈[t2,∞)T时有X(t)>0.否则若X(t)<0,可推得

其中φ(t,t1)由(3)式定义.

证设x(t)是(1)的一个最终正解且满足引理2.1中的情形(i),则b(t,x(t))((a(t)x∆(t))∆)γ是单调减的.于是对(a(t)x∆(t))∆>0从t1到t>t1积分,可得

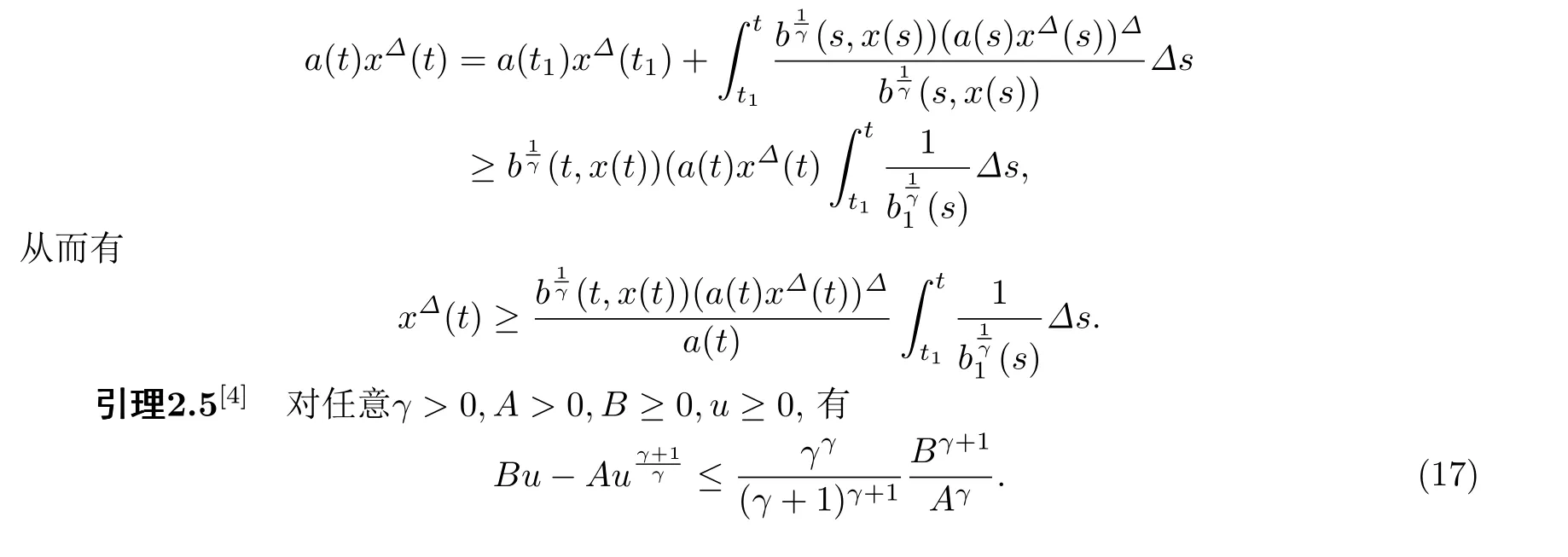
§3 主要定理及其证明

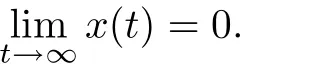
注1容易看出当b(t,x(t))=b(t),a(t)=1时,方程(1)将变为方程(6).因此本文定理3.1完全包含了文献[4]中的定理2.1.文献[6]研究了γ≥1,b(t,x)=b(t)时方程(10)的振动性,本文的γ>0,因此,本文定理3.1也拓展了文献[6]定理4.1的应用范围.

注2由定理3.1可知选择不同的δ(t)函数,可以得到不同的振动条件,例如当取δ(t)=1时,可得著名的Leighton型振动定理,当δ(t)=t时,也可得到相似的重要振动定理,限于篇幅,这里从略了.因此,本文丰富和统一了所列文献及其引文中包括三阶微分方程和差分方程的振动性结果.

下面的定理是关于方程(1)的Philos型振动准则.

证假设方程(1)有一个非振动解x(t),不失一般性,可设存在足够大的t1∈[t0,∞)T,使得当t∈[t1,∞)T时,有x(t)>0,x(τ(t))>0.则对于所有t∈[t1,∞)T,由引理2.1可知x(t)满足情形(i)或情形(ii).

如果情形(i)成立,则类似于定理3.2的证明可得(29)式成立,即

注3本文定理3.2和定理3.3推广了文献[4,6]的研究,即同时将函数b(t)拓展到b(t,x),将函数H(t,s)的定义域

扩展到

和将γ≥1扩展到γ>0的情形.易见本文定理3.3完全包含了文[4]的定理2.2和文[6]的定理4.3并将其条件中的积分上限σ(t)精确为t,且本文定理3.2拓展了文[6]定理4.2关于γ的应用范围.

下面的定理是关于方程(1)的Kamenev型振动准则.

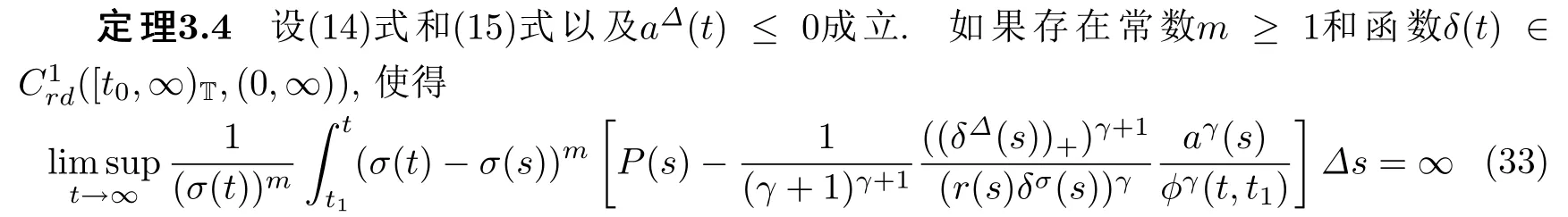
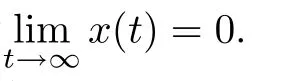
证假设方程(1)有一个非振动解x(t),不失一般性,可设存在t1∈T,使得当t∈[t1,∞)T时,有x(t)>0,x(τ(t))>0.由引理2.1,可知x(t)满足情形(i)或情形(ii).

若为情形(i)成立,则类似于定理3.1的证明可得(25)式成立,即有

§4 应用举例

考虑三阶非线性时滞微分方程

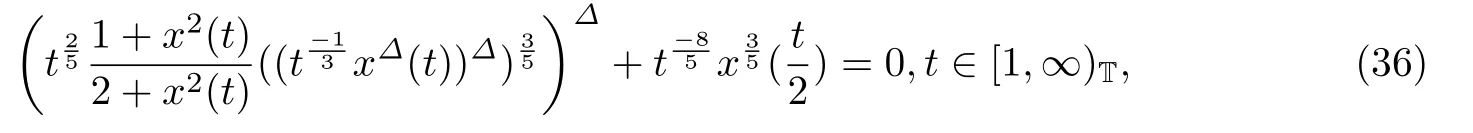
的振动性.

对照方程(1),这里