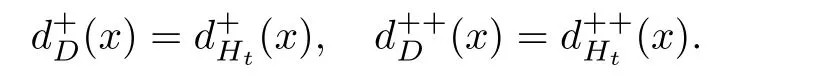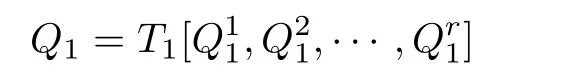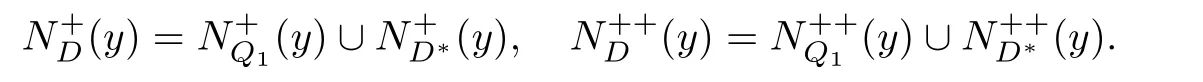准传递定向图上的Seymour点
李瑞娟,史 杰,张新鸿
(1.山西大学数学科学学院,山西太原030006;2.太原科技大学应用数学系,山西太原030024)
§1 引 言
Seymour提出的关于定向图的二次邻域的问题是有向图理论中最有趣,最具挑战性的问题之一.这里,定向图是指没有2圈的有向图.本文涉及到的有向图是无环,无平行边的简单有向图,相关的术语和符号参看下一小节以及文献[1].
猜想1.1[2](Seymour二次邻域猜想) 在定向图D中,总可以找到一个顶点x,这个顶点的二次外邻域至少和它的外邻域一样大,即d+(x)6d++(x).
根据文献[3],这样的顶点x称为Seymour点.
值得注意的是,猜想1.1只适用于定向图,并不适用于一般的包含2圈的有向图.例如,n个顶点的完全有向图,对于每个顶点,都有即

把Seymour二次邻域猜想限制到竞赛图上,称为Dean猜想.Fisher在文献[4]中,利用Farkas引理,证明了Dean猜想[2],得到以下结论.
定理1.1[4]在任何一个竞赛图T中,都包含一个Seymour点.
Havet和Thomass在文献[5]中给出了Dean猜想更基本的证明,并介绍了一种叫中间序的方法.他们的证明也得到了以下更强的结果.
定理1.2[5]若竞赛图T无出度为零的顶点,则T至少包含两个Seymour点.
文献[6]进一步发展了中间序的方法,证明了猜想1.1对于最小度为|V(D)|−2的有向图D也同样适用.同样地,猜想1.1对于竞赛图减去一颗星,竞赛图去掉子竞赛图的弧集也同样适用.Ghazal在文献[7]中也使用了中间序的方法,证明了猜想1.1对于加权竞赛图去掉广义星同样适用.Kaneko和Locke在文献[8]中证明了猜想1.1对于最小出度最多为6的定向图也同样适用.Cohn,Godbole,WrightHarkness和Zhang在文献[3]中证明了该猜想对于某些随机定向图也适用.
证明猜想1.1的另一种方法是确定极大值γ,使得在每个有向图D中存在一个顶点x满足. 在猜想1.1中,γ=1.Chen,Shen和Yuster在文献[9]中证明了γ≥r,其中r=0.657298···是2x3+x2−1=0的唯一实根.若对证明方法细化,他们还可以得到r≥0.67815···.近年来,二次邻域问题被更多人研究,参看文献[10-12].
本文将证明Seymour二次邻域猜想在准传递定向图上的正确性,通过研究准传递定向图的Seymour点与扩张竞赛图的Seymour点之间的关系,得到:每个准传递定向图至少包含一个Seymour点;无出度为零的点的准传递定向图至少包含两个Seymour点.
§2 术语,符号和基本结论
设D是一个有向图,分别用V(D)和A(D)表示D的顶点集和弧集.
若有向图D中的不同顶点u和v,存在从u到v的弧,则称u控制v,写成u→v,并称v是u的外邻点或者u是v的内邻点.若对于D的一个子有向图或仅仅是D的一个顶点子集H(可能有H=D),H中顶点u的外邻点的集合用表示,称它为H中顶点u的外邻域.另外,称为u在H中的出度.设

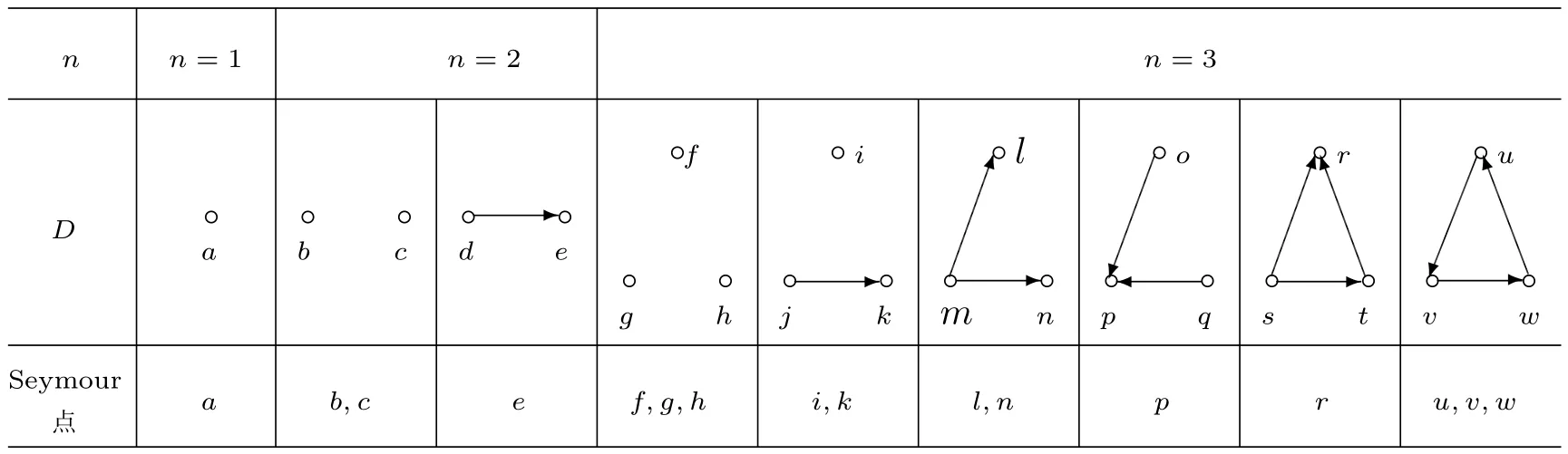
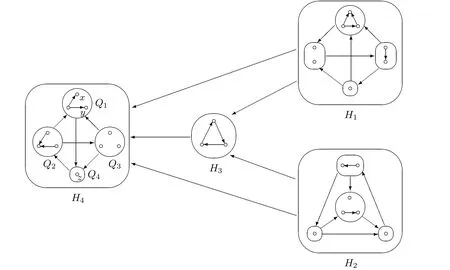
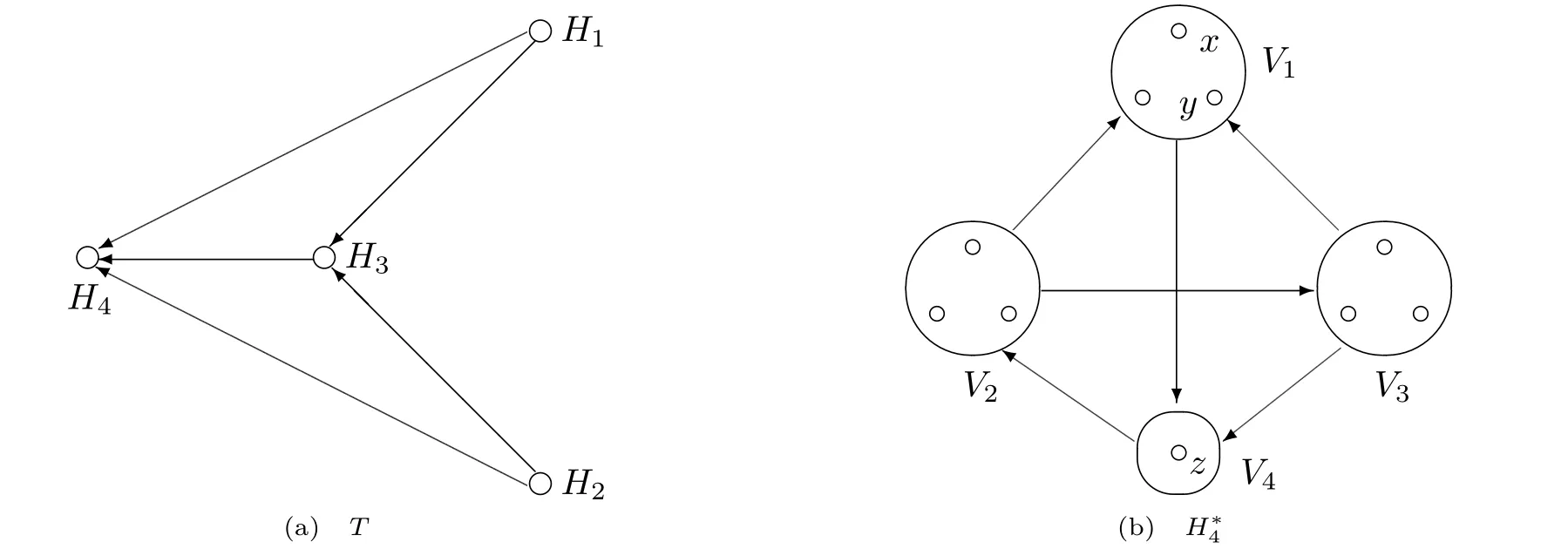
如果有向图D没有有向圈,那么它就是无圈的.如果对于无圈有向图D的每一对弧xixj∈A(D),满足i 若D=H[S1,S2,···,Sh],且每个有向图S1,S2,···,Sh都没有弧,则称D是H的扩张.这时对每个i∈{1,2,···,h},Si称为D的部集.若有向图中每对不同的顶点都相邻,则称这个有向图为半完全有向图.没有2圈的半完全有向图称为竞赛图.扩张竞赛图是指一个竞赛图的扩张.对于有向图D中的三个不同的顶点x,y和z,若在D中存在弧xy,yz,在x和z之间总存在一条弧,那么称有向图D是准传递的.若在D中存在弧xy,yz,在x和z之间总存在弧xz,那么称有向图D是传递的.显然每个传递有向图是准传递的,每个扩张竞赛图也是准传递的. 为了简化准传递有向图上某些结论的证明,Bang-Jensen和Huang在文献[13]中给出了这类有向图的结构刻画. 定理2.1[13]设D是一个准传递有向图,则 (a)若D是非强连通的,则存在一个传递定向图T,它的顶点集为{u1,u2,···,ut},还存在强连通的准传递有向图H1,H2,···,Ht,使得D=T[H1,H2,···,Ht],其中对于任意的i∈{1,2,···,t},Hi代替了ui. (b)若D是强连通的,则存在一个强连通的半完全有向图S,它的顶点集为{v1,v2,···,vs},还存在准传递有向图Q1,Q2,···,Qs,使得Qi不是单点就是非强连通的,且D=S[Q1,Q2,···,Qs],其中对于任意的i∈{1,2,···,s},Qi代替了vi. 定理2.1中描述的分解称为准传递有向图D的典型分解. ' 图1 一个非强连通的准传递定向图D的典型分解 更多有关准传递定向图的结论参看文献[14-20]. 本文研究的是Seymour二次邻域猜想对于准传递定向图同样适用,因为准传递定向图是准传递有向图没有2圈时的特殊情况,所以在运用定理2.1时,需要取其没有2圈的情况,也就是要把准传递有向图用准传递定向图代替.同样地,半完全有向图用竞赛图代替. 如图所示,给出了一个非强连通准传递定向图D的典型分解,这个典型分解可表示为D=T[H1,H2,H3,H4],其中,T为一个传递定向图,如图2(a)所示;对于任意的i∈{1,2,3,4},Hi是强连通的准传递定向图.图1中的大弧表示不同框集之间在显示方向上有一个完全控制. 这部分考虑强连通准传递定向图的Seymour点与扩张竞赛图的Seymour点之间的关系.为此,先考虑图1的最后一个强分支H4,它是一个强连通的准传递定向图,对于任意的i∈{1,2,···,s},用Qi的顶点集Vi代替Qi,得到一个扩张竞赛图,如图2(b).容易验证,V1和V4中的点都是中的Seymour点;x,y是Q1中的Seymour点;z是Q4中的Seymour点;x,y,z是H4中的Seymour点.由此可得,Q1和Q4中的Seymour点都是H4中的Seymour点. 图2 传递定向图T和扩张竞赛图 引理3.1设D是一个强连通的准传递定向图,它的典型分解为D=S[Q1,Q2,···,Qs].设D∗=S[V1,V2,···,Vs]是一个扩张竞赛图,其中,对于任意的i∈{1,2,···,s},Vi是子有向图Qi的顶点集.若存在一个顶点v∈Vi,使得v是Qi的一个Seymour点,同时也是D∗的一个Seymour点,那么v也是D的一个Seymour点. 证因为v是Qi中的一个Seymour点,也是D∗中的一个Seymour点,则有 由于D∗是扩张竞赛图,显然有 这部分考虑扩张竞赛图上的Seymour点.首先证明猜想1.1对扩张竞赛图是成立的. 定理4.1每个扩张竞赛图至少包含一个Seymour点. 证设D=S[V1,V2,···,Vs]是一个扩张竞赛图,其中每个Vi都是一个独立集.现用一个和Vi有相同顶点集的传递竞赛图代替每个Vi,这样就得到了一个新的有向图D0.显然,D0是一个竞赛图,由定理1.1得,D0存在一个Seymour点,设为x,即有又有 此外,定理1.2也可以推广到扩张竞赛图中.事实上,可以得到更强的结论,即如果这两个Seymour点在同一部集中,则至少有一个点的二次外邻域的顶点个数严格大于一次外邻域的顶点个数. 定理4.2设D=S[V1,V2,···,Vs]是一个扩张竞赛图,且每个Vi是独立集.若D中无出度为零的顶点,则 (a)D中至少包含两个Seymour点; (b)D中至少存在一个Seymour点x,使得,除非存在另一个和x在不同部集的Seymour点y. 证设D=S[V1,V2,···,Vs]是一个扩张竞赛图.现用一个和Vi有相同顶点集的传递竞赛图代替每个Vi,这样D就变成了一个新的竞赛图T.因为D无出度为零的顶点,所以T的每个顶点出度也不为零.根据定理1.2,T中至少包含两个Seymour点x,y,则显然 则x,y也是D上的Seymour点,故(a)成立. 若这两个Seymour点x,y在不同的部集中,则(b)成立.故假设这两个Seymour点x,y在相同的部集中,即有某个i∈{1,2,···,s},x,y∈Vi.不失一般性,假设在T中x控制y.因此 由此可得(b)成立. 这部分考虑准传递定向图上的Seymour点.设D是一个准传递定向图,它的阶数为n.表1列出了当n=1,2,3时所有的准传递定向图,并在表1的第三行中指出对应图的Seymour点. 表1 n=1,2,3时所有的准传递定向图及其Seymour点 下面证明猜想1.1对准传递定向图是成立的. 定理5.1每个准传递定向图至少包含一个Seymour点. 证设D是一个准传递定向图,通过对D的阶数n进行归纳证明.参看表1,易知当1≤n≤3时,结论成立.现假设n≥4. 情形1D是非强连通的. 设D=T[H1,H2,...,Ht]是D的典型分解,其中,T是传递定向图,且对i∈{1,2,···,t},Hi是强连通的准传递定向图.不失一般性,现假设H1,H2,···,Ht是D的强分支无圈序.通过归纳假设,设x是Ht的Seymour点,则.显然 情形2D是强连通的. 设D=S[Q1,Q2,···,Qs]是D的典型分解,其中,S是强连通的竞赛图,且对i∈{1,2,···,s},Qi是单点或者非强连通的准传递定向图.设D∗=S[V1,V2,···,Vs]是一个扩张竞赛图,其中,对i∈{1,2,···,s},Vi都是子有向图Qi的顶点集.由定理4.1可知,D∗有一个Seymour点x.现假设x∈Vi,则Vi的每个顶点都是D∗中的Seymour点.由归纳假设,Qi有一个Seymour点,也记为x.则由引理3.1可知,x也是准传递定向图D中的一个Seymour点. 根据定理5.1的证明,在图1所示的准传递定向图D中,最后一个强分支H4中的Seymour点就是D中的Seymour点.通过观察,顶点x,y,z是H4中的Seymour点,也是D中的Seymour点.又注意到,在图1所示的准传递定向图D中,每个顶点的出度都不为零,且D包含的 Seymour点多于1个.现证明,定理1.2可以推广到准传递定向图中. 定理5.2设D是准传递定向图,若D中无出度为零的顶点,则D中至少包含两个Seymour点. 证现通过对D的阶数n进行归纳证明.显然n≥3.参看表1,易知当n=3时,结论成立.现假设n≥4. 情形1D是非强连通的. 设D=T[H1,H2,···,Ht]是D的典型分解,其中,T是传递定向图,且对i∈{1,2,···,t},Hi是强连通的准传递定向图.不失一般性,假定H1,H2,···,Ht是D的强分支无圈序.因为D无出度为零的顶点,所以最后一个分支Ht至少包含3个顶点,即Ht是一个每个顶点出度都不为零的准传递定向图.通过归纳假设,在Ht中至少包含两个Seymour点.因为Ht中的每一个Seymour点也是D的Seymour点,所以D中至少包含两个Seymour点. 情形2D是强连通的. 设D=S[Q1,Q2,···,Qs]是D的典型分解,其中,S是强连通竞赛图,且对i∈{1,2,···,s},Qi是单点或者非强连通的准传递定向图.设D∗=S[V1,V2,···,Vs]是一个扩张竞赛图,这里对i∈{1,2,···,s},Vi是子有向图Qi的顶点集.显然D∗是强连通的且无出度为零的顶点.由定理4.2(b)可得,要么存在一个Seymour点x,使得;要么存在另一个和x在不同部集的Seymour点y.在后面这种情况下,D∗有两个属于不同部集的Seymour点,记这两个部集为Vα和Vβ.由归纳假设,对每个i∈{1,2,···,s},Qi都至少包含一个Seymour点.特别地,Qα和Qβ中都包含Seymour点.再由引理3.1可知,Qα和Qβ中的Seymour点也是D的Seymour点.因此在这种情形下D包含两个Seymour点. 现考虑前面一种情形,即D∗中存在一个Seymour点x,使得为了方便,设x∈V1.如上所述,Q1中的Seymour点,仍记为x,也是D的Seymour点.下面寻找D的另一个Seymour点. 首先断言部集V1中至少包含2个顶点.否则,x是V1中的唯一顶点.由定理4.2(a)知,D∗中存在另一个不在V1的Seymour点y.如上所述,y所在的部集中必存在D的另一个Seymour点.结论成立.故假设V1至少包含2个顶点. 如果Q1至少包含两个Seymour点,则它们也是D中的Seymour点.故假设Q1恰好只有一个Seymour点x. 现断言V1中存在一个不同于x的顶点y,使得.设 是Q1的典型分解,其中,T1是一个传递定向图,且对是强连通的准传递定向图.类似地,假定是Q1的强分支无圈序.易知,是唯一的终止强分支,且x是中唯一的顶点.否则,Q1中会有除x外的其它Seymour点,与假设矛盾.由归纳假设,在中存在一个Seymour点y,则.现有 从而断言成立. 因为y和x在D∗的相同部集V1中,所以它们的外邻域和二次外邻域在D∗中是相同的,从而不等式也成立.显然 综上所述,该定理成立.
§3 准传递定向图和扩张竞赛图的Seymour点的关系
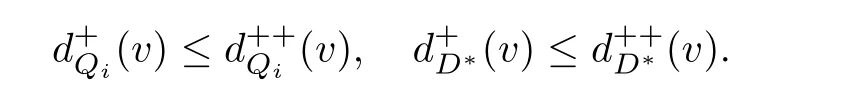

§4 扩张竞赛图的Seymour点
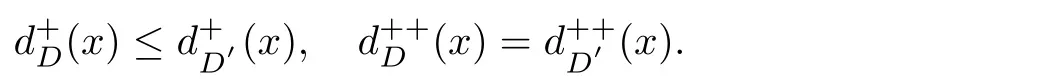
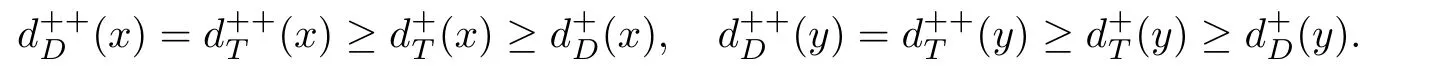
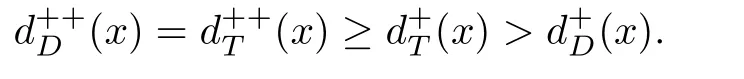
§5 准传递定向图的Seymour点