基于对偶的不精确交替方向乘子法求解核范数正则化最小二乘问题

史冰冰, 王青松

(1.西南交通大学数学学院,四川成都611731;2.北京航空航天大学数学科学学院,北京100191)

§1 背景简介

核范数正则化最小二乘问题来源于仿射秩最小化问题,而秩最小化本质为矩阵补问题,即通过矩阵的一部分信息,求解整个矩阵信息对其补充.矩阵秩最小化在图像恢复,图像去光照影响,图像矫正与去噪及智能系统推荐等各个领域取得了相应的成果.

可以通过求解以下优化问题恢复秩为r的大多数矩阵M:

其中M∈Rn×n,并且该矩阵有m个采样项Mij:(i,j)∈Ω,其中Ω是基数m的随机子集.然而问题(1)通常是NP难的非凸优化问题,[1]证明了经过突松弛最小化了核范数,进而将问题转化为:

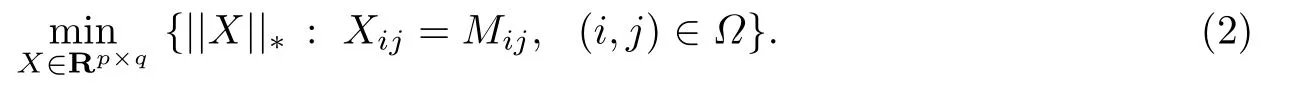
此处考虑更一般的形式[2]:

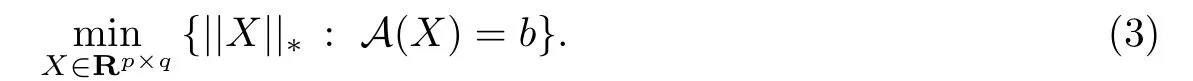
若从问题(1.1)的约束角度考虑,Fazel[3]和Boyd[4]对仿射秩最小化问题做凸松弛转化为以上核范数问题(3).此类一般约束形式的核范数最小化问题早已在各个领域得到充分发展,包括机器学习[5-6],控制问题[4,7-8]以及欧几里德嵌入[9]等.

但是实际观测到的b往往带有噪声,那么A(X)=b可能是不可行的,必须放宽该约束.因此寻求最小化残差||A(X)−b||2,并考虑如下核规范正则化最小二乘问题[10],即:

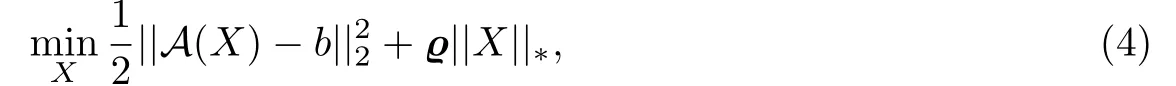
其中A:Rp×q→Rm是一个线性映射,||X||∗是迹范数(也被称为核范数)为矩阵X的所有奇异值之和,%>0为正则化参数,b∈Rm.

针对问题(4)已经有很多种求解方法.根据[11]的工作,问题(4)可以等价转化为半正定规划问题(Semidefinite Programming Problem(SDP)),用求解SDP的方法来求解,比如[12-13].然而,这些求解器不适用于p,q规模较大的问题,因为在这些求解器的每次迭代中,即使数据稀疏也必须求解大规模的线性方程.

为了克服求解SDP的缺陷,最近也出现很多方法.Cai[2]等人提出的奇异值阈值算法求解(3)的相似模型,即

其中τ>0为给定的参数,||X||F表示矩阵X的Frobenius范数.

最近Ma等人[14]通过逼近奇异值分解过程提出了固定点连续算法(Fixed Point Continuation with Approximate SVD)用以求解(4).另外Chen[15]等人利用交替方向法求解类似(2)的带有噪音的矩阵完备化问题,经过对问题形式转换分解为可分割的两项交替求解.

Toh和Yun[16]提出了一种加速的临近梯度法来求解问题(4),该文章的工作中通过线性搜索来加速算法收敛速度,但是在做线性搜索时需要随时注意参数的选择,以使得不至于步长过小而收敛速度变慢.本文将考虑从问题(4)的对偶形式出发利用交替方向乘子法求解该问题.

§2 预备知识

2.1 基本概念及符号说明

本节来说明优化中常用的一些符号以及概念[17].

1)若H1和H2是希尔伯特空间,A:H1yH2是一个有界线性算子,如果算子A∗:H2yH1,对于所有的x∈H1,y∈H2,满足:hAx,yi=hx,A∗yi则称A∗为A的希尔伯特伴随(共轭)算子.

2)对于某一实的有限维希尔伯特空间X上的子集C,C上的指示函数定义为:δC(x),即:δC(x)=0,当x∈C；δC(x)=+],当x/∈C.

3)函数f:Rn→R,那么函数f的共轭函数f∗定义为:

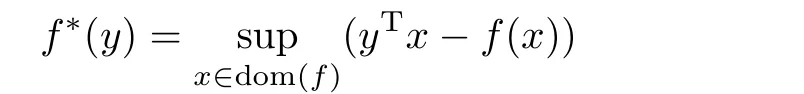
4)对于给定的闭的真凸函数f:X→(−∞,+∞],与f相关的临近点映射Proxf(.)定义为:

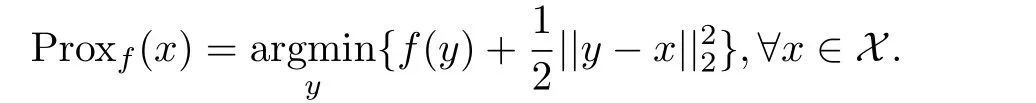
5)矩阵内积:设A,B∈Rn×n,称(vecA)T(vecB)为矩阵的内积.其中Trace(A)为矩阵A的迹,简记为Tr(A);vecA=(a11,a12,···,a1n,a21,a22,···,a21,···,an1,an2,···,ann)为矩阵A的向量化.

2.2ADMM

简单介绍一下ADMM算法框架,该方法用以求解带有等式约束或小于等于型不等式约束,并且其中变量可分开交替求解的模型.最早由Glowinski和Marrocco[18]以及Gabay和Mercier[19]提出,该方法普遍应用于大规模问题及机器学习等领域.此类问题一般形式如下:

其中f:Xy(−],+]]和g:Xy(−],+]]是闭的真凸函数,A:XyZ和B:XyZ是线性算子,X,Y,Z是实有限维欧几里得空间,该空间上内积定义为:h.,.i,其诱导范数为:||.||.此问题增广拉格朗日函数:

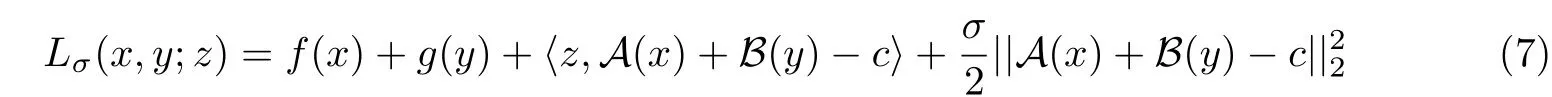
求解(6)的ADMM具体算法框架如下:

§3 算法

3.1 求解问题(1)的不精确dADMM

令p(X)=%||X||∗,则可以将问题(4)改写为:

现在给出求解问题(9)的不精确dADMM算法.

3.2 子问题

本小节给出不精确dADMM算法中求解子问题的详细步骤,即关于变量z和W的求解,具体过程如下:

问题(14)有唯一解析解,可以通过对G作奇异值分解求解.假设G的奇异值分解为:

其中U∈Rp×s和V∈Rq×s都是具有正交列的矩阵,ξ∈Rs是分量为矩阵G的正奇异值组成的向量,按降序排列ξ1≥ξ2≥···≥ξs>0,s≤min{p,q}.对于给定的向量X∈Rs,令x+=max{x,0},其中最大值是按分量获取的,即x每个分量与0的最大值.由[16],问题(14)的解为:

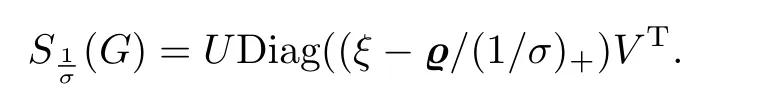
因此根据G的奇异值分解,可以解得关于w的闭形式的解

3.3 不精确dADMM算法的收敛性

本节说明求解对偶问题的不精确dADMM算法的收敛性.参照文献[20]和[21]的定理5.1建立该算法的全局收敛性,具体过程可参考文献[21],此处只考虑其中S=0,T=0的情况:

式中：α和β分别为价值函数收益区域和损失区域的凹凸系数[24]，表示X方主体对待收益和损失的风险态度，α,β∈(0,1);λ为损失规避系数[25]，表示X方主体的损失规避程度，λ>1。

推论1假设对偶问题(11)的解集非空,约束条件成立.若(zk+1,wk+1,Xk+1)是由不精确dADMM算法产生,其中,那么序列(zk+1,wk+1)收敛到对偶问题(11)的最优解,而Xk+1收敛到原问题(4)的最优解.

§4 数值实验

实验在64位Windowins 10操作系统的联想笔记本电脑上实现的,电脑配置为:Intel(R)Core(TM)i7-7500U CPU@2.70GHz 2.90GHz,4G运行内存,运行环境为MATLAB 2017b.

以下实验中,对于给定的p,q,m,映射A(X)=(hA1,Xi,hA2,Xi,···,hAm,Xi),A∗(y)=,即矩阵A的每一列为Ai的向量化,定义A的矩阵形式

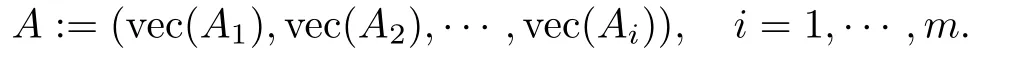
4.1 停机准则

为了检测逼近最优解的程度,定义KKT(Karush−Kuhn−Tucker)残差：

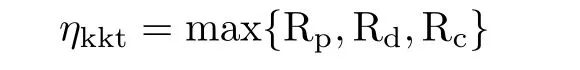
其中

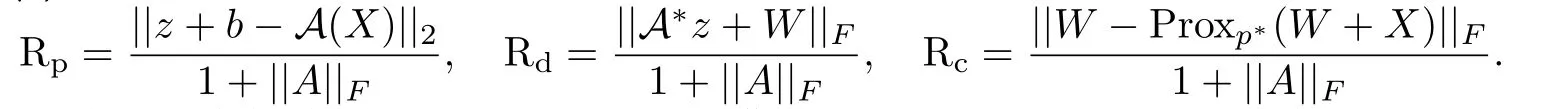
对于给定的精度,算法如果满足ηkkt<10−5或者迭代次数超过10000次,则停止迭代.

4.2 实验

1)不同维度对比

本小节通过随机数据对比不同维度的矩阵,迭代步数,满足停机准则时的误差及对应时间的变化.对于给定的p,q,m,Ai和b都是随机产生的稀疏数据.计算单位为:秒(s)

表1 dADMM算法下不同维度数据数值结果

2)对比从原问题和对偶问题用不精确ADMM算法

通过引入变量Y,问题(4)转化为:

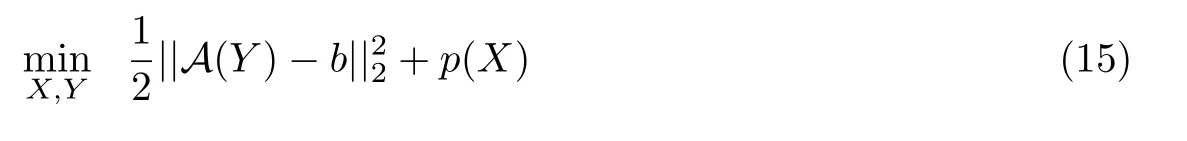
问题(15)的增广拉格朗日函数为:

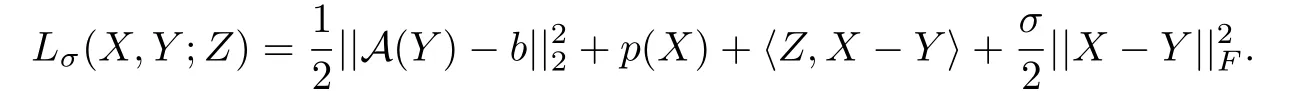
现在给出求解问题(15)的不精确ADMM算法.

通过将核范数最小二乘问题原始模型形式转化与对偶问题做迭代次数,停机准则及计算时间上的对比.对于给定的p,q,m,Ai和b都是随机产生,计算单位为:秒(s),具体比较结果如下:

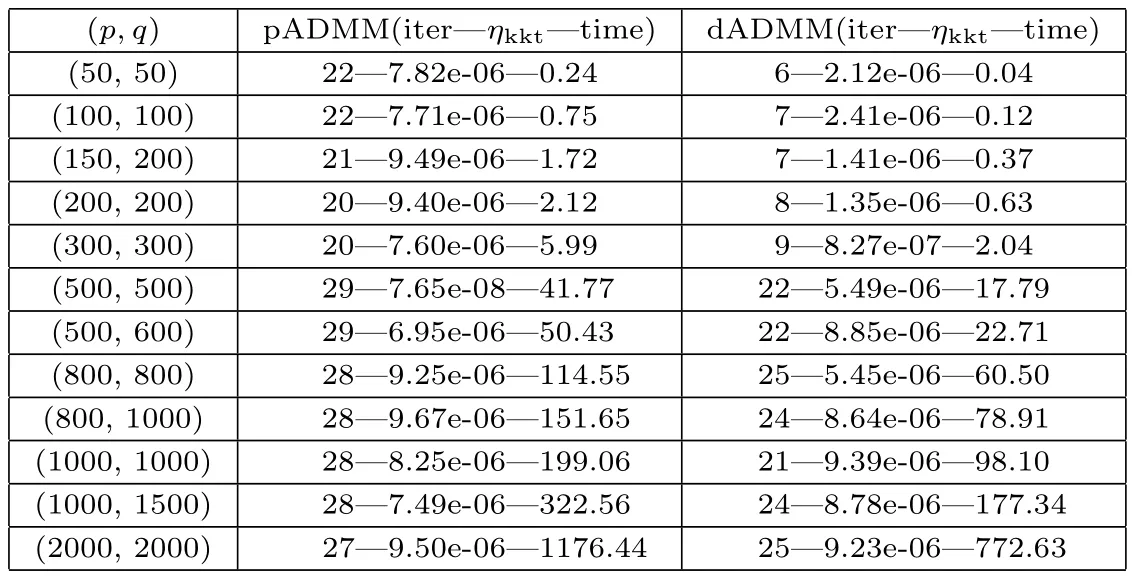
表2 dADMM算法和pADMM算法对比

通过对比以上结果,得到从对偶解决该问题明显比从原始问题做消耗时间更少,迭代次数也相对较少,成本更低.

另外对比对偶和原始不精确ADMM算法迭代计算中前后两次解的相对误差

此处令p=100,q=100,产生随机数据做数值实验,随着迭代次数变化规律,误差对比如下:

图1 dADMM算法和pADMM算法前后两次解误差对比

随着迭代次数增加相对于从原问题出发的不精确ADMM,不精确的dADMM方法前后两次求解所得最优解的相对误差明显变化趋势波动较小且接近于0.因此足够说明我们从对偶问题出发求解核范数最小二乘问题的优越性和稳定性.

3)多变量线性回归模型

本节将参照文献[16]中的做法,对多变量线性回归模型[22]通过形式转换,求解如下拉格朗日松弛问题.通过随机产生数据来说明不精确dADMM方法在多变量线性回归问题中应用的优越性.

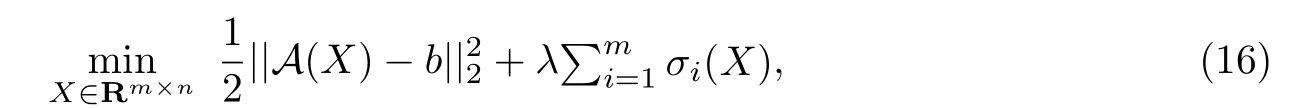
其中A(X):=vec(ΛX),Λ∈Rm×m是一个正定对角矩阵,λ≥0.

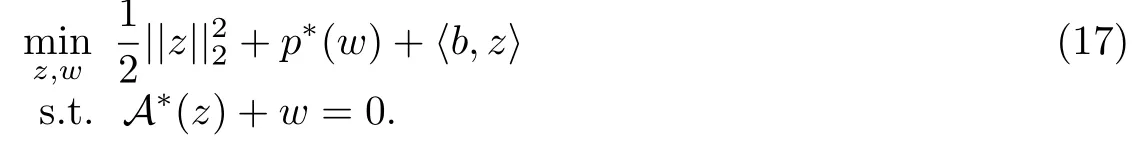
其中w∈Rm×n.

如下对不精确的dADMM与文献[16]中的APGL做KKT残差和时间对比,其中对于给定的m,n及Λ=diag(rand(m,1)),M=randn(m,r)∗randn(r,n),R=randn(m,n),b=vec(ΛM+0.01||ΛM||F/||R||FR),计算单位为:秒(s).通过以上对比可以得到,随着维度增大不精确的dADMM算法迭代次数变化并不是多大,所用时间明显增加.相比于APGL算法,不精确dADMM算法所需时间及迭代次数更少,更具有稳定性.

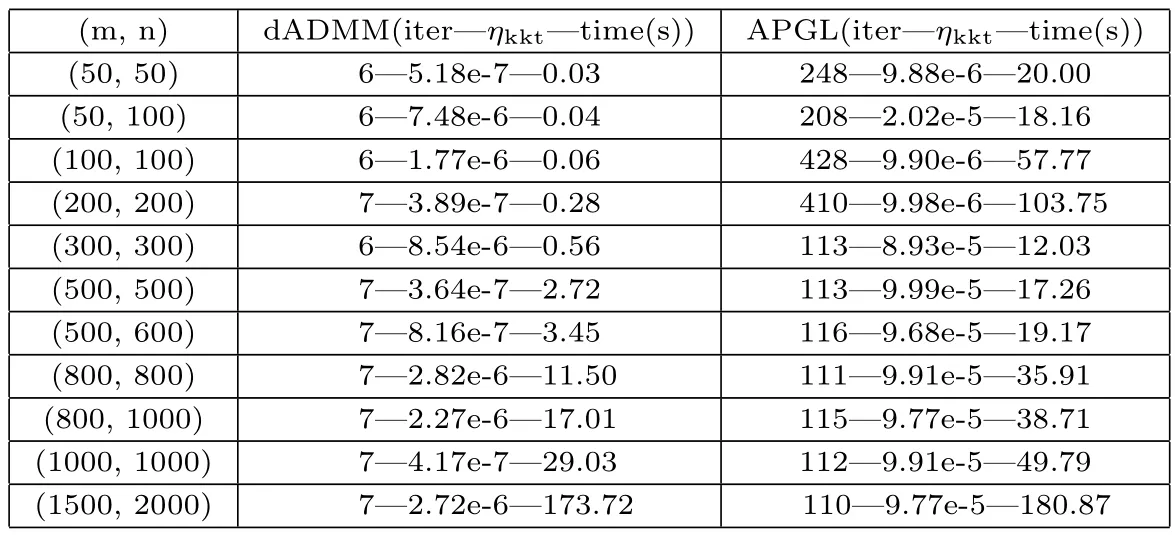
表3 dADMM算法和APGL算法对比

此处令m=n=1000,按上述方法产生随机数据,分别从KKT残差和每次迭代所需时间对比不精确dADMM算法和APGL算法,计算单位为:秒(s).

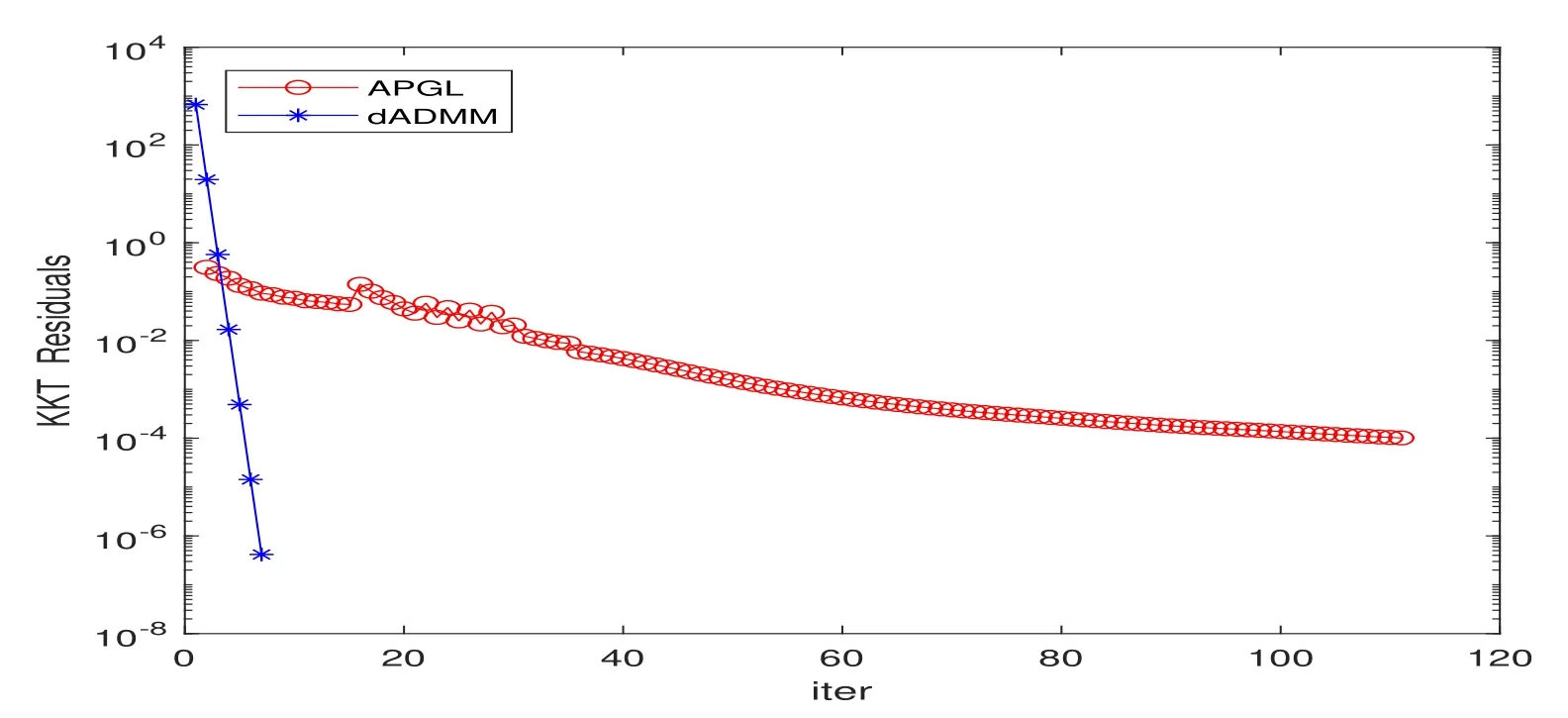
图2 dADMM算法和APGL算法KKT残差对比

从不精确的dADMM算法和APGL算法下的多变量线性回归模型的对比,明显不精确的dADMM算法KKT残差收敛后相对更小,且收敛更快.

图3 dADMM算法和APGL算法时间对比

对不精确的dADMM算法和APGL算法下的多变量线性回归模型做每步时间上的对比,明显不精确的dADMM算法每步迭代时间相对更少,更具高效性.

§5 总结

通过不精确的ADMM算法求解核范数正则最小二乘问题的对偶模型进而解得原问题,同时在一定假设条件下说明该优化算法的全局收敛性.通过相应的实验,说明了本文算法的高效性和稳定性,可以在更少的迭代次数内求得该问题.