基于Hoek-Brown准则和极限分析的极软岩临坡地基承载力计算方法及应用

孙立川，赵在立，张清林

(河北中核岩土工程有限责任公司，河北省石家庄市裕华区兴苑街53号 050021)

在工程建设实践中，由于地形条件的限制及工程需要，常常要将构筑物的基础放置在斜坡地基上或者是临近斜坡坡肩的位置。此外，在已有建筑基础附近进行基坑开挖，也会引起地层变形和建筑物地基承载力减损。而对于岩质边坡，当出现临坡地基问题时除了按照岩质边坡进行局部稳定分析(平面滑动、楔形体滑动、倾倒破坏)和整体稳定性计算外，也应研究岩质边坡的临坡地基承载力减损问题。

现有文献中对于临坡地基承载力问题的研究大都集中于基于摩尔-库伦准则(也即c～φ边坡)的土质边坡，对于岩质边坡的临坡地基承载力问题，特别是极软岩边坡的临坡地基承载力鲜有涉及。

近年来，基于经验且适用于岩石和岩体的广义Hoek-Brown非线性经验破坏强度准则得到了广泛的应用。我国学者进行了大量的把Hoek-Brown非线性经验破坏强度准则转换成摩尔-库伦强度准则的研究[1-6]。

现有规范中地基承载力计算公式是基于半无限空间的普朗德尔承载力公式[2-3]，是根据均质、无重土体等假设推导的。而临坡地基的承载力问题是半无限空间被破坏，形成了斜坡地基的承载力问题，因此文中应用Hoek-Brown准则和极限分析原理进行临坡地基承载力计算。

1 相关理论和规范简述

1.1 临坡地基承载力的概念

郑刚[9]等研究了c～φ边坡的坡面破坏、坡趾破坏、基底破坏、坡体失稳破坏和普通破坏共5种破坏模式对极限承载力的影响，各种破坏模式形态如图1所示。对于相同的边坡坡体，当破坏模式不同时，地基承载力会有显著不同。此类地基承载力受边坡存在的影响，与地表水平的半无限空间中的地基承载力有质的区别。

图1 边坡滑动破坏模式[9]Fig.1 Slope sliding failure mode[9]

印度学者Saran等[10]考虑“边坡-地基”的应力扩散特征和破坏变形形状，基于极限平衡理论，采用极限分析法，分析了基底三角形楔体的不对称性以及边坡的存在对地基极限承载力的影响(见图2)。

图2 Saran斜坡极限承载力理论示意图[10]Fig.2 Theoretical sketch of Saran ultimate bearing capacity of slopes[10]

胡卫东基于梅耶霍夫理论，考虑基础两侧埋深土体抗剪强度、基础两侧侧壁与土体摩擦作用对承载力的影响，建立了单侧滑移破坏模式的临坡地基承载力公式[11]。

1.2 规范对临坡地基承载力的规定

1.2.1 建筑边坡工程技术规范

《建筑边坡工程技术规范》(GB 50330-2013)[12]对如何确定坡顶地基承载力没有明确规定，仅在7.2.1.5-6条笼统地指出：在坡顶有重要建筑物时，应考虑边坡变形对地基承载力和基础变形的不利影响，并应对建筑物基础和地基稳定性进行验算；边坡支护结构距离基础外边缘的最小安全距离应满足坡顶建筑物抗倾覆、基础嵌固和传递水平荷载的要求，其值应根据设防烈度、边坡稳定性、岩土构成、边坡高度和建筑物高度等因素结合地区工程经验综合确定，不满足时应采取有效加固措施。

1.2.2 建筑地基基础设计规范

《建筑地基基础设计规范》(GB 50007-2011)[13]指出，位于稳定土坡坡顶上的建筑物，对于条形基础，当垂直于边坡边缘线的基础底面边长小于或等于3 m时，其基础至坡肩的水平距离应符合下式要求，且不得小于2.5 m，即

(1)

式中：a为基础至坡肩水平距离；b为垂直于坡顶边缘线的基础底面边长；d为基础埋深；β为边坡坡角。

当不考虑基础埋深时(即式(1)中d=0 m)，基础应置放于3.5倍基础宽度之外。

1.2.3 重庆市建筑地基基础设计规范

重庆市建筑地基基础设计规范[14]给出了按照岩体完整性和坡角估算坡顶承载力的经验公式(平地承载力折减)：“对位于无外倾结构面、岩体完整、较完整或较破碎且稳定的岩质边坡上的基础(见图3)，边坡地基承载力特征值可根据平地地基承载力特征值折减估算，折减系数可根据基础外边缘与坡脚连线倾角按表1确定”。该折算方法适用于较破碎、较完整、完整岩体且坡体稳定的岩质边坡。

图3 边坡滑动破坏模式Fig.3 Slope sliding failure

表1边坡地基承载力折减系数
Tab.1Reductioncoefficientofbearingcapacityofslopefoundation

边缘与坡脚连线倾角90°～75°75°～50°50°～15°折减系数0.33～0.500.50～0.670.67～0.85

1.3 极限分析上下限定理简述

针对符合正交流动法则及直线强度包线的材料(即标准Coulomb材料)，Drucker等人将静力场和运动场结合起来，并提出极值原理，建立了极限分析理论[15-16]。

极限分析法是通过一组极限定理即上限定理或下限定理，推求极限荷载的上限或下限。上限解仅满足机动条件与屈服条件，应力场服从机动条件或塑性功率不为负的条件；下限解仅满足平衡条件和不违背屈服条件。上限解和下限解彼此独立从极限荷载的上限方面和下限方面逐渐趋近极限荷载。

文中利用optumG2软件通过极限分析上下限定理求解临坡地基承载力问题。

1.4 基于波速的Hoek-Brown准则简述

E.Hoek和E.T.Brown在狭义Hoek-Brown准则的基础上，于2002年提出了广义的Hoek-Brown非线性经验破坏强度准则经验公式[17-20]：

(2)

式中：σ1，σ3分别为破坏时岩体的最大和最小主应力，MPa；σc为岩块单轴抗压强度；mb为岩体的Hoek-Brown常数，与完整岩块的mi相关；s，α为取决于岩体特征的系数。其中，mb，s，α均可表示为地质强度指标GSI(Geological Strength Index)和岩体受扰动程度参数D的函数：

(3)

式中：GSI为与岩体结构、岩体中岩块的嵌锁状态及结构面表面特征有关的参数；D为爆破破坏和开挖卸荷对岩体的扰动程度；mi为完整岩块的Hoek-Brown准则常数，反映岩石的软硬程度，可由室内三轴试验计算或者查文献[1]确定。

李硕标[2]推导出岩体纵波速度与RMR的关系：

RMR=(40VP+10)/3

(4)

其中，RMR为1976版本RMR76(不考虑结构面产状影响)，当RMR76>18(VP>1 100 m/s)时，GSI=RMR。

用Dv表示扰动因子D，将GSI和Dv代入式(2)，得到改进公式：

(5)

式中下标v代表岩体参数。

岩体抗剪强度参数内摩擦角φ和黏聚力的计算式[3-4]，[21]为：

(6)

其中

(7)

另外，对于均质岩石边坡工程和隧道工程，最小主应力上限值σ3max表示如下[3-4]，[21]：

(8)

式中：γ为岩体重度，Hs为边坡的坡高，Ht为隧道埋深，σcm为岩体抗压强度。

岩体抗压强度按下式计算：

σcm=σc×

(9)

林达明[6]基于宋建波[21]公式推导的岩体地基极限承载力为：

qult=q0+(mq0σc)αv+{mσc[q0+(mq0σc+

(10)

2 工程应用

2.1 工程概况

国外某核电站按照中国规范设计、施工、建造。该核电项目需开挖JB廊道，断面如图4所示，北边坡坑深(图4右侧边坡)10.12 m。坡顶距离基坑边缘4.265 m处有一个核岛施工用自重式塔吊，塔吊基础为8 m×8 m筏板基础，基础及塔吊总重约11 000 kN。根据塔吊基础设计计算书，塔吊基础埋深0 m，工作状态时最大偏心荷载240 kPa，非工作状态时最大偏心荷载302 kPa。拟建场地基岩为晚第三系上新统泥岩和砂岩，主要为泥岩(见表2)。

图4 基坑开挖断面图及塔吊位置示意图Fig.4 Section diagram of foundation pit excavation and sketch diagram of tower crane position

根据建设周期和甲方要求，自重式塔吊属于重要设备，使用周期大于2年，JB廊道施工周期约1年。根据《建筑边坡工程技术规范》(GB 50330-2013)，基于安全考虑，按照一级临时边坡考虑，边坡稳定安全系数不能小于1.25。

表2 岩石的主要指标Tab.2 Main indicators of rocks

根据甲方提供的塔吊设计计算书，塔吊基底最大偏心压力为302 kPa。由于塔吊吊臂方向的随机性，按照均布荷载等于最大偏心荷载考虑，即JB管廊基坑开挖后坡顶塔吊位置处地基承载力不得小于302 kPa，且总体沉降和差异沉降(倾斜)不得大于原设计要求的数值以及规范要求，以保证塔吊设备正常运转。

边坡坡体为中风化泥岩和微风化泥岩，属于极软岩。虽然对工程场地曾进行过详细勘察，但详勘报告中没有提供岩体的抗剪强度指标黏聚力c和内摩擦角φ(仅有岩石抗剪强度指标)，也没有提供岩体的GSI或者RMR指标，但提供了跨孔波速测试结果以及常规物理力学参数(表2)。现甲方要求验证边坡稳定性，并分析边坡开挖对塔吊基础的影响，以便在保证塔吊正常运转不受影响的情况下，确保边坡稳定和施工安全。同时，限于管沟施工时大型预制管道吊装要求，不能使用内支撑形式的支护结构。

2.2 抗剪强度指标

利用式(4)得到中等风化泥岩和微风化泥岩的RMR，分别为24.49和31.84。因这2种岩体的纵波波速均大于1 100 m/s，故GSI=RMR，则中等风化泥岩和微风化泥岩的GSI分别为24.49和31.84。由式(5)计算Hoek-Brown准则参数，结果如表3所示。

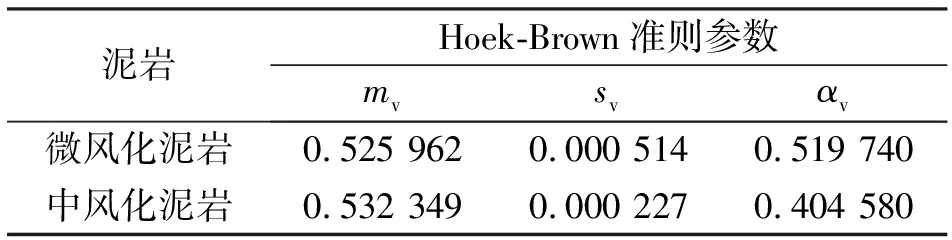
表3 Hoek-Brown准则参数表

根据式(8)，抗剪强度指标因工程性质(隧道或者边坡)而不同，且与围压σ3max密切相关。根据本工程设计数据(图4)，边坡总高度12.4 m，其中中风化深度约6 m，微风化岩体深度12.4 m(其中微风化泥岩厚度约6.4 m)。根据现场地质情况和施工条件，可以确定不用炸药即可机械开挖施工，故没有爆破扰动。另自然地坪标高不大，开挖深度不大，卸荷影响可忽略不计，故Dv=0。由式(5)计算中等风化泥岩和微风化泥岩岩体抗剪强度指标，见表4。

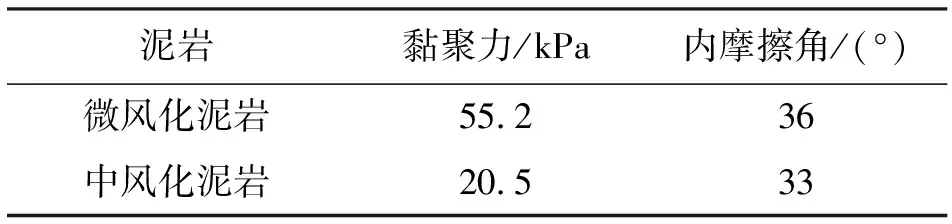
表4 岩体抗剪强度计算结果Tab.4 Shear strength of rock mass calculated by Hoek-Brown criterion

需要指出的是，上述岩体黏聚力为岩块相互嵌合形成的机械咬合力，不同于粘性土的化学胶结、黏粒间的电荷吸力和分子吸力等所形成的黏聚力。与之类似的实例可参考炸山块石回填层的开挖坡角可做到很陡却不坍塌，表现出一定的“黏聚力”。

2.3 抗剪强度指标的合理性验证

把上述计算所得到的各个参数代入式(10)即可计算岩体极限承载力。按照规范规定，岩体地基承载力安全系数取3.0，由此可得地基承载力(表5)。

采用optumG2软件进行数值极限分析时，按照半无限空间体，考虑地层岩性为中风化泥岩、微风化泥岩建立计算模型，分别进行极限分析。岩体黏聚力和摩擦角采用表4中的数值，分析所得的剪切耗散图见图5，每种风化程度的上下限的乘数荷载(数值上等于极限荷载)见图表说明，将其除以安全系数3.0即得每种风化岩体的地基承载力上下限解，真实的地基承载力解即位于上下限解之间，见表5。

表5 平板载荷试验成果和计算值对比表

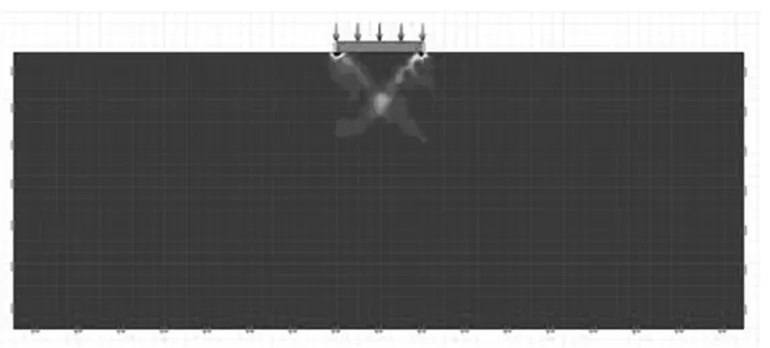
(a)下限解(乘数荷载2783)

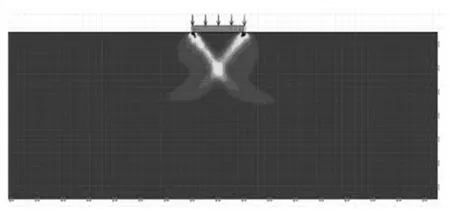
(b)上限解(乘数荷载3953)图5 中风化泥岩半无限空间的极限分析剪切耗散示意图Fig.5 Shear dissipation schematic of limit analysis in semi-infinite space of moderately weathered mudstone

对该工程核岛详勘时，曾经在中等风化和微风化泥岩埋深较浅的位置开挖至相应地层，对2类风化程度岩体进行了6组岩基平板载荷试验(表5)。

从表5可见，根据Hoek-Brown准则计算的地基承载力、按照极限分析上下限定理采用optumG2软件计算的地基承载力与载荷试验结果吻合度很高，说明了上述各个参数的准确性。故此，由上述Hoek-Brown准则的各个参数所计算的抗剪强度指标黏聚力c内摩擦角φ是合理、可靠的。

3 边坡稳定性

3.1 考虑结构面确定滑动破坏模式及可能性

根据节理调查结果，对边坡按照节理面进行组合，分析不同节理面交叉组合形成的块体滑动可能性，结果表明，此岩质边坡主要的潜在破坏方式为直接倾倒破坏。但需要指出的是，以上仅为节理切割的块体沿节理面有滑动的可能性，是否滑动还取决于岩体强度和结构面强度以及外荷载作用情况。

3.2 不考虑岩体结构面的整体稳定性

把该边坡视为均值边坡，按照上述计算所得的岩体抗剪强度指标，坡顶均布荷载取前述塔吊基础最大荷载302 kPa，采用optumG2软件按强度折减法计算的安全系数FS仅为1.15，位移为6.9 mm；而用GEO5软件按照极限平衡法计算的安全系数FS也只有1.14，边坡稳定安全系数不满足规范要求(见图6)。

(a)强度折减法(FS=1.15)

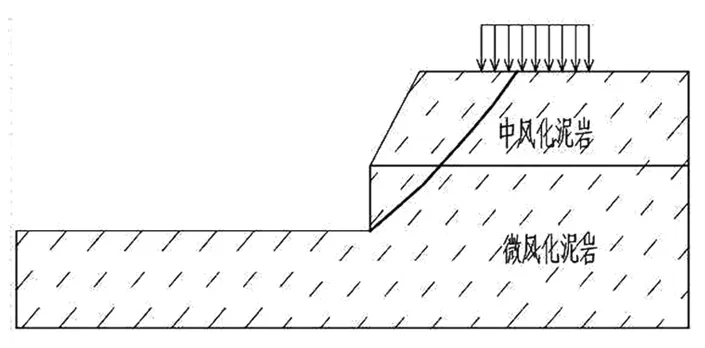
(b)极限平衡法(FS=1.14)图6 强度折减法(下限解)和极限平衡法计算结果示意图Fig.6 Schematic diagrams of strength reduction method(lower bound solution) and limit equilibrium method

4 重庆市基础设计规范适用性的讨论

本工程边坡岩体为极软岩，岩体完整性指数为较完整，从前述极限平衡法和强度折减法的计算结果来看，属于潜在不稳定边坡。

现暂不考虑边坡的潜在不稳定性(FS=1.14>1.0)，也即假设该边坡属于稳定边坡。按照表1和图4所示边坡坡角52°考虑，则折减系数保守取值为0.5，按照载荷试验确定的中风化泥岩平地地基承载力见表5，计算折减后的坡顶地基承载力约为650 kPa，大于302 kPa。而即使按照表1中最小折减系数0.33进行计算，坡顶承载力约为430 kPa，也满足302 kPa的要求，但是这个承载力是否可靠存疑。

由于上述边坡为极软岩，而规范的建议更多的是考虑普遍的、常见的情况，从上述计算的边坡稳定性不满足要求，而承载力计算结果却大于302 kPa要求来看，重庆市建筑地基基础设计规范[14]地基承载力经验折减法不适用于本工程极软岩边坡。

上述问题的关键在于载荷试验确定的承载力与基于半无限空间、地表水平的普朗德尔公式相统一，在基础两侧均存在“无限”的土体(岩体)阻挡滑移线的扩展，滑移线上由岩土体自重以及黏聚力等提供的剪切阻力对承载力有很大的贡献作用(图2)。而本工程由于挖除了侧边岩土体，减少了这种阻力，导致承载力降低。

当岩体强度较高时，岩体自身的抗剪强度就可以提供这种剪切阻力，故基础侧边部分挖除后对岩质边坡坡顶地基承载力的影响相对较小，此时，可以按照重庆市建筑地基基础设计规范进行折减后使用。而极软岩岩质边坡的岩体强度很低，岩体自身抗剪强度提供的这种剪切阻力也很小，对挖除基础侧边岩土体非常敏感，此时按照规范经验进行折减的承载力就会与实际情况相去甚远。

总之，该工程边坡属于潜在不稳定边坡，重庆市建筑地基基础设计规范[14]确定地基承载力的方法不适用于本工程极软岩岩质边坡。

5 临坡地基承载力的上下限数值解和极限平衡解

按照塑性力学上下限定理，进行数值极限分析，可分析复杂应力、复杂边界条件下的地基极限承载力问题。当上下限解相等时为精确解，当上下限解不等时，真实的承载力数值介于上下限解之间。

采用由Hoek-Brown准则计算的抗剪强度指标参数(表4)进行极限分析，地基极限承载力上下限解结果分别为673 kPa和781 kPa，即地基极限承载力真实解介于673 kPa和781 kPa之间(限于篇幅，图7仅列出下限解的剪切耗散示意图)，考虑可静应力场的下限解和考虑可动应力场的上限解差别不大，所得结果近乎地基承载力的精确解。根据规范，岩质地基安全系数取3.0，则地基承载力为224～260 kPa，小于302 kPa，不满足要求。

另外，根据胡卫东[11]基于梅耶霍夫理论建立的临坡地基承载力公式计算的极限承载力为636 kPa，安全系数同样取3.0，则得地基承载力为212 kPa，计算结果与下限解相近，同样不满足要求。

图7 下限解剪切耗散示意图(乘数荷载673)Fig.7 The calculation model diagram of slope top and the upper bound solution shear dissipation diagram

6 加固后的边坡稳定性和地基承载力

考虑到工程地点位于国外，采购备料、运输存在困难，决定采用两根φ25螺纹钢，钻孔直径φ110的全长粘结型锚杆进行加固。横向间距2.0 m，竖向间距1.5 m，长度7.0～13.5 m不等，为此建立计算模型，如图8和图9(a)所示。

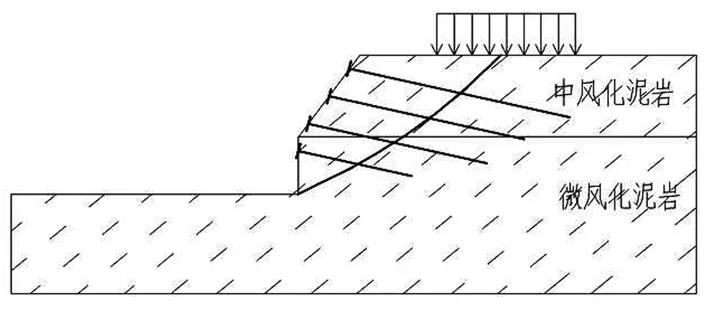
图8 极限平衡法模型计算结果示意图Fig.8 Schematic diagram of calculation results of limit equilibrium method model

(a)计算模型

加固后，用极限平衡法计算的边坡稳定系数FS为2.15，满足要求。用optumG2软件按强度折减法计算的边坡安全系数为2.14，最大位移为4.48 mm，同样满足规范要求(图9(b))。

加固后地基极限承载力下限解为3 177 kPa，上限解取平地承载力上限解3 953 kPa和加固后的上限解5 463 kPa中的小值(见图10)。安全系数同样取3.0，地基承载力为1 050～1 320 kPa，大于302 kPa，满足要求。加固后边坡最大位移4.48 mm。

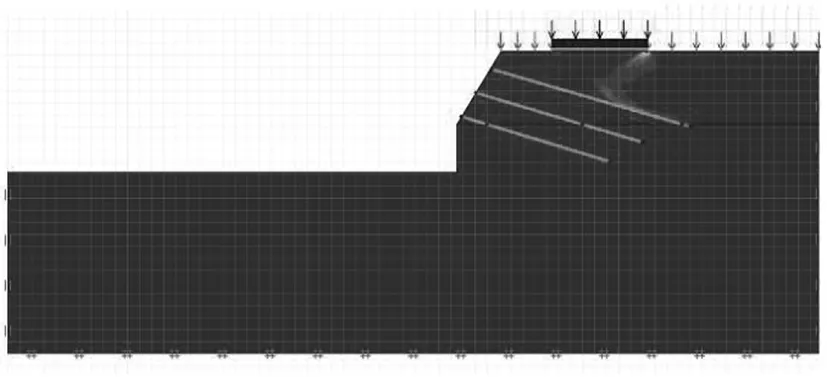
(a)下限解(乘数荷载3177)

(b)上限解(乘数荷载5463)图10 加固后极限分析剪切耗散示意图Fig.10 Shear dissipation diagram of limit analysis after reinforcement

7 结论

(1)采用广义Hoek-Brown非线性经验破坏强度准则结合勘察报告中纵波波速可以较为准确地推算地质强度指标，从而获得Hoek-Brown强度准则的参数，并据此计算摩尔库伦抗剪强度指标。

(2)从地基承载力的计算结果(公式(10)和极限分析法)和平板载荷试验结果对比来看，采用上述Hoek-Brown强度准则参数计算的摩尔库伦抗剪强度指标符合工程实际情况，参数合理、可靠。

(3)使用软件利用极限分析上下限定理计算斜坡坡顶地基承载力合理可行，有准确的理论依据，能解决复杂应力条件、复杂边界条件下的地基极限承载力问题。

(4)采用文献[11]基于Meyerhof理论建立的临坡地基承载力公式的计算结果和利用极限分析下限定理的计算结果相近，两者相互印证，进一步说明了结果的合理性。

(5)未加固的边坡，稳定性安全系数1.15，小于最低1.25的规范要求，坡顶地基承载力仅为224～260 kPa，小于302 kPa，不满足要求，且塔吊基础也不稳定，边坡需要进行加固。

(6)采用锚杆加固后的边坡是稳定和安全的，安全系数FS=2.14，大于建筑工程边坡技术规范最低1.25的要求。加固后的坡顶地基承载力为1 050～1320 kPa，大于302 kPa，承载力满足要求。加固后塔吊所在边坡最大沉降仅为4.48 mm，经计算，塔吊基础总体沉降和倾斜均满足要求。

综上，文中极软岩临坡地基承载力和稳定性问题的求解方法对于开挖引起地层变形和建筑物地基承载力减损等方面有借鉴意义。对于城市建设中地铁隧道开挖对已有建筑物地基承载力减损、新开挖基坑对地铁的影响等也有一定借鉴意义。