一类食饵有传染病的捕食者-食饵模型的动力学分析
刘宣亮,熊 艳
(华南理工大学数学学院,广东 广州 510640)
1 数学模型
近几十年来,人们在种群动力学和传染病动力学方面做了大量的研究工作,随着研究的深入,疾病在种群之间传播的生态-流行病模型也引起广泛的关注和研究[1-7],如文献[3-4,7]研究了疾病在食饵中传播的捕食者-食饵模型,文献[5-6]研究了疾病在捕食者中传播的捕食者-食饵模型.本文考虑疾病仅在食饵者中传播,且具有垂直传染和饱和传染率的一类捕食者-食饵模型:
(1)

为简化模型,做如下变换:
则由方程(1)可得到系统
(2)
2 解的有界性


(ⅰ)若s(τ)+i(τ)≥1对任意的τ≥0都成立,则当τ→+时,(s(τ),i(τ),y(τ))→(1,0,0)或(s(τ),i(τ),y(τ))→(0,1,0);
(ⅱ)若存在某个时间τ0≥0,使s(τ0)+i(τ0)<1,则当τ>τ0时,s(τ)+i(τ)<1.
证明:(ⅰ)对于任意的τ≥0,s(τ)+i(τ)≥1.由系统(2)的前两个方程可得
(3)

矛盾,所以有
(4)
由方程(3)、(4)有
(ⅱ)若存在τ1>τ0,使得s(τ1)+i(τ1)=1,则有

于是当s(τ0)+i(τ0)<1时,对τ>τ0,有s(τ)+i(τ)<1成立.证毕.

证明:令X(τ)=a3(s(τ)+i(τ))+y(τ),则
-a4(a3s+a3i+y)+a3[(a1+a4)s-a1s2+(a2+a4)i-a2i2)]≤
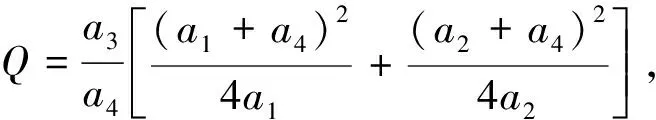
a3(s(τ)+i(τ))+y(τ)≤max{a3(s(0)+i(0))+y(0),Q},

3 边界平衡点及其稳定性
(ⅰ)平衡点P1(0,0,0)和P2(1,0,0)总是存在且是不稳定的.
(ⅱ)平衡点P3(0,1,0)总是存在,当a3
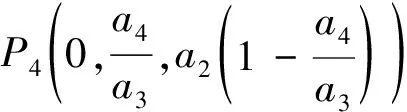
4 正平衡点及其存在性

(5)
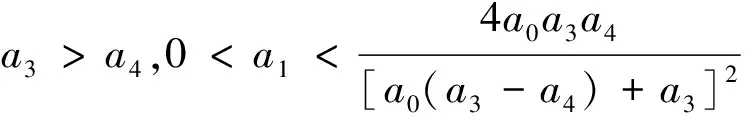
5 正平衡点的分支
(6)
下面讨论系统(6)在正平衡点P0(s0,i0,y0)附近的Hopf分支和Bogdanov-Takens分支.
系统(6)在正平衡点P0处的雅可比矩阵为
其中:
其对应的特征方程为
λ3+c1λ2+c2λ+c3=0,
(7)
其中:c1=-(a+d),c2=ad-bc-ef,c3=aef.
5.1 Hopf分支
对系统(6)作如下变换
v1=s-s0,v2=i-i0,v3=y-y0,
则系统(6)变为
(8)
其中:V=(v1,v2,v3)T,F(V)=(F1,F2,F3)T,
若矩阵A1的特征方程(7)有一对纯虚根±iω0(i为虚数单位,ω0>0),将iω0代入方程(7),可得c1c2-c3=0,即
Δ=-a2d-ad2+abc+bcd+def=0.
(9)

由系统(8)的非线性项以及文献[9],取关于x=(x1,x2,x3)T,y=(y1,y2,y3)T和z=(z1,z2,z3)T的对称多线性向量函数
根据文献[9]中一阶Lyapunov系数的计算公式:
可求得l1(0).但由于l1(0)的表达式太长,不易讨论其正负.下面取一组特定的参数值来计算l1(0),从而得到此时的Hopf分支的方向.
故在正平衡点P0附近有超临界Hopf分支产生.当0 设系统(6)在正平衡点P0(s0,i0,y0)的特征方程(7)有两个零特征值,于是有 c2=0,c3=0, 则有 a=0,bc+ef=0. 此时特征方程(7)的特征值分别为0、0、-c1,且-c1=d<0. 将上式代入bc+ef=0,可得 其中:X=(s,i,y)T∈3,U=(a1,a2)T∈2.记则F(X0,U0)=0,DF(X0,U)=A1.F(X,U)在(X0,U0)处的泰勒展开式为 F(X,U)=DF(X0,U0)(X-X0)+FU(X0,U0)(U-U0)+ 注意到b0c0+ef=0,由A0p1=0,A0p2=p1,A0p0=d0p0,可得 现规定记号如下: 利用文献[10],计算可得 (q2·(FUX(X0,U0)-(A2FU(X0,U0))TD2F(X0,U0)))p1= 其中: (10) (11) 其中: 由文献[10],可得如下结论: (ⅱ)有Hopf分支曲线:H={(λ1,λ2):η1=0,η2<0}; 相应的分支曲线如下: 本文对一类食饵有传染病且有垂直传染的捕食者-食饵模型进行了动力学分析,首先得到了模型的解的有界性,即随着时间的增加,捕食者、易感食饵及染病食饵的数量都是有界的,然后讨论了正平衡点的Hopf分支和Bogdanov-Takens分支. 根据5.1节的Hopf分支的结论可知:当初值和参数适当选取,模型(2)可产生稳定极限环,即随着时间的增加,易感食饵、染病食饵和捕食者数量呈周期性变化而不消失.根据5.2节的Bogdanov-Takens分支的结论可知:当参数选取适当,可分别出现三种分支曲线SN、H和HL,表明模型(2)除可由Hopf分支产生极限环外,还可通过鞍结点分支产生两个正平衡点(即有地方病出现),以及通过同宿分支出现同宿轨和产生极限环,即模型中易感食饵、染病食饵和捕食者数量将产生周期性震荡.5.2 Bogdanov-Takens分支


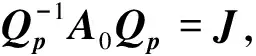

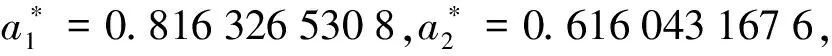
6 结 论

