浅谈小学低年级数学《几何直观》画图教学策略
曾庆欣

数学是一门抽象、高度概括性的学科。对于思维相对简单的小学生而言,要学好数学这门学科并不简单。低年级的学生以形象思维为主,抽象思维能力较弱,作为“几何直观”教学的重要途径之一——“画图策略”的地位就尤为重要。这种教学方法对教师教学和学生学习都有极大的帮助。
一、激发“画”的意识,感知“几何直观”的优越性
低年级学生思维较为简单,对比较抽象的数量关系,或者条件更为复杂的题目,理解起来是有一定困难的。如低年级教材里面,经常会看到类似这样的题目,“小东前面有5人,后面有6人,这一行一共有多少人?”一开始,80%的学生都会列了5+6=11的算式,能正确解答的学生少之又少。可如果当你画出这样的一幅图:
学生们一定会冲口而出,说出正确答案。
解决“比多少”的实际问题,一直是低年级学生学习的难点。谁和谁比,谁比谁多,谁比谁少难以分清,甚至一看到题目出现“比多”就加,“比少”就减的错误逻辑情况。曾做过一实验,如教师只是出现文字信息:红花有8朵,比黄花多3朵,黄花有多少朵?部分学生还是会用“5-3=2”来解答,因为他们分不清谁比较多,谁比较少。而若用图示法:
再次让学生回答谁比较多,谁比较少时,意见非常统一,全部正确。
通过纯文字及图示两种方法的对比,学生能明显感受到画图策略,利用几何直观的好处。同时,教师亦可顺势引导,可以通过圆圈、三角形、其他符号等去表现人或事物。
二、掌握“畫”的方法,为运用“几何直观”提供保障
“画”的方法不是与生俱来的,几何直观教学也必须是一个长久的过程。在一年级的学习中,学生在教材与学习过程中已初步感知到,可以用小圆片等表示具体物体的数量,如:5个苹果,可以用5个小圆形表示,进而再抽象出可以用数字“5”来表示。当然,想学生学会用线段去表示“5”,直接告知,并不是最好的方法。在解决问题的过程中产生冲突,进而想方法解决才是最优的。如,可以用5个小圆形表示数字“5”,那怎么去表示“50”呢?当然,还是会有学生提出用50个小圆形来表示,教师可以让其上来黑板画;另外再询问还有没有其他的方法,由聪明的学生或教师介绍画线段的方法。只需要在画上一条小横线,上面标上“50”,就可以代表“50”了。而此时,刚才提议画小圆形的学生还在黑板上画,强烈的对比,让学生显而易见地感受到,有时候用线段比画图形来得更简便。教师继而发问:“这是一条表示50的线段,那如果表示30,用线段怎么表示?40呢?100呢?”同时,教师在日常教学中,也可继续介绍大括号、集合圈等符号的作用。
在潜移默化的渗透过程中,学生便渐渐掌握了“画”的方法,为以后运用“几何直观”解决问题提供了保障。
三、激发“画”的兴趣,规范“几何直观”的表达
当然,画图的策略对于低年级学生来说,没有唯一性,教师只是起到了示范、启发与指导的作用。
在课堂上,鼓励学生用自己喜欢的方式画图,激发学生画图的兴趣,并抓住教学契机让学生展示自己的作品,说出自己的想法,及时对学生进行表扬鼓励,激发学生运用画图策略的热情。并采取了一系列的措施,来激发学生的画图兴趣:比如上课时让学生在黑板上画图,然后师生共同评析,看哪个同学画得好,优点在哪里,存在哪些毛病;印发常见的基本直观图给学生,让学生反复观摩,然后再画出来;数学活动课中还组织学生进行“画直观图比赛”。这些措施激发了学生的学习兴趣,使学生认识到规范作图的重要性,增强了学生的画图能力。
学生爱“画”还要会“画”,教师要规范学生的画图习惯。首先,通过多种途径和方式,使学生真正体会画图对理解概念、寻求解决思路带来的益处。其次,要求学生解决问题时能画图的尽量画图,将相对抽象的思考对象“图形化”,尽量把数学的过程变得直观,直观了就容易展开形象思维。再次,要让学生规范画图,能准确直观的表达题意。
四、培养“画”的意识,提升“几何直观”解决问题的素养
将几何直观用于描述和分析“非几何与图形”领域的问题时,恰恰最能彰显几何直观的价值。这样教学,能更好地培养学生的几何直观意识与能力,最终提升几何直观素养。
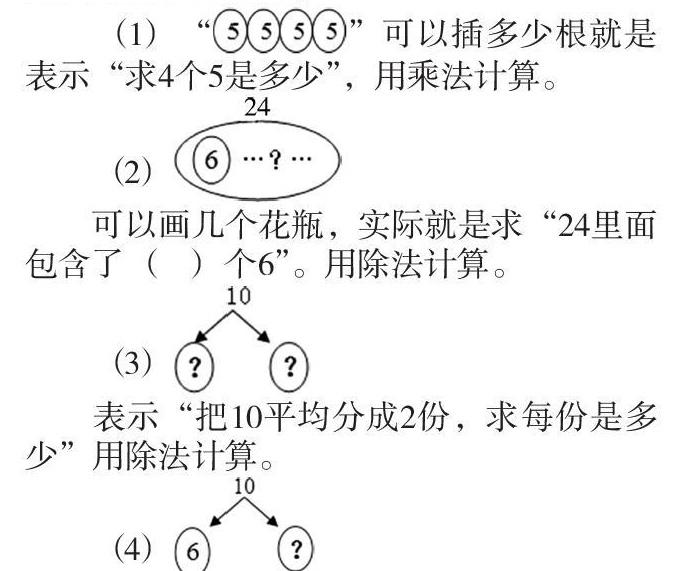
教学二年级《表内除法》这一单元时,学生常常会对信息复杂而又相近的题目无所适从。如书本第27页第4题,这是一道综合性非常强的一道题。(1)每个花瓶插5根羽孔雀毛,4个花瓶可以插多少根?(2)每个花瓶插6根孔雀羽毛,24根孔雀羽毛可以插几个花瓶?(3)有10根孔雀羽毛,平均插在2个花瓶里,每个花瓶插几根?(4)有10根孔雀羽毛,插在2个花瓶里,一个花瓶插6根,另一个花瓶里插几根?
在集备时,教师们对此内容进行过探讨,方法各异:一种是认为要教给学生数量关系式,如:每份数×份数=总数;总数÷份数=每份数;总数-部分数=部分数……依据这样的关系式子,让学生去“分析”,去“用”,好比建筑工地的脚手架。但是,从学生们一脸茫然的表情中,我们得知,套用公式的做法并不能让学生真正理解算理。另一种声音就是靠“多说”,教师示范学生跟说,多说几次学生就能理解了。可是,这样做,忽视了“理解不是建立在说之上,而是会说应该建立在理解之上”。还有一种就是,“让学生画图理解”。拿到题目,可以边读边根据题意画出草图,根据草图再一次理解题意,然后寻求解决问题的办法。
如刚才的4小题我们可以通过这样的直观图帮助学生理解:
经过一段时间的训练,我们发现,学生若能画出草图,对题目的意思也就理解相当正确了,在解决问题列式时也就显得颇有头绪了。
总之,“画”在探究数学知识中确实藏有博大精深的奥妙。画图策略与几何直观有着千丝万缕的关系。借助画图教学,可以培养和发展学生的几何直观能力,感悟初步的数形结合思想。重要的是,学生能通过画图将复杂的数学问题变得简明、形象,以便更快地找到解决问题的方法。发展好学生的图形语言,培养几何直观能力,能为后续更好地学习较复杂的几何知识打下良好的基础。

