儿童空间观念的发展策略
杭菁


摘 要:“空间观念”作为新课标十个核心概念之一,高度凸显了其内涵特征和价值,儿童空间观念的培养需要我们重新考查衡量图形几何教学的实质,让学生形成独特的思维方式。本文从作图教学、联结迁移两个方面,对儿童空间观念的发展策略展开阐述。
关键词:空间观念 发展策略
在几何课程中,空间观念被认为是数学能力中的重要部分,儿童空间观念的发展,对于帮助他们理解、解释和欣赏我们现实的几何世界是十分关键的,也能为今后进一步系统学习几何知识打下良好的基础。下文从两个方面对儿童空间观念的发展策略展开阐述。
一、作图教学:铺好空间观念发展的奠基石
美国数学家斯蒂思曾指出,如果一个特定的问题可以转化为一个图形,那么就整体地把握了问题,并且能创造性地思考问题的解法。因此,学会作图是学生的空间观念、解决问题能力得以发展的基本途径 ,我们要帮助学生建立“画图是一种发现问题、分析问题、解决问题的策略”的意识,将作图教学贯穿始终,使学生形成用图说话,用图推理,用图解决问题的良好习惯。
1.培养读图能力
纵观教材我们可以发现图文并茂是一大特点,无论是例题还是练习的设计,都需要学生去阅读、发现、理解图中隐含的线索,因此,提高学生的读图能力刻不容缓。
如:《观察物体》中的习题
教学中应引导学生观察:①和③虽然都是三个正方形,但由于方向不同,①是竖着的,③是横着的,因此①是从上面看到的形状,而③是从右面看到的形状。
小学生的思维模式,以感性思维比较多,也是向抽象思维过渡的一个阶段,这个阶段可以以读图为起点,配合实物或者模型操作,图形结合、化虚为实,给学生带来真实、丰盈的感知,积累大量的表象,建立起图像与立体图形的空间联系,形成“空间知觉”。
2.示范作图方法
儿童模仿能力强,他们的作图习惯、作图方法、作图能力往往是從教师的作图示范中模仿学来的。因此,教师的言传身教极为
重要。
例如在教授画一定长度的线段时,教师应一边示范,一边讲解:先确定线段的一个端点,再将直尺的0刻度线对齐这个端点,再从左往右根据线段长度确定另一个端点并画出线段。虽然这些内容看起来很细小,但却是学生作图能力后续发展的基础。
3.体会作图价值
要让学生心甘情愿作图,那就首先要让学生体会作图价值:图形特点越画越鲜明,数量关系越画越清晰,思维越画越顺畅,思考越画越深入。激发了学生运用作图解决问题的意识,他们才会产生作图的意愿。
以《长方形的周长》一课中的习题为例:一块长方形木板,长24米,宽16米,锯下一个最大的正方形,正方形的周长是多少米?剩下木板的周长是多少?这一题如果让学生想象,空间思维好的学生能想象出来,但对于基础较差,空间思维较薄弱的孩子来说肯定有一定难度,如果画画图,这道题的难度就大大降低了。
这张图将锯下的正方形和剩下的长方形特征直观表现出来,文字信息缩减了,却更明了了,既能帮助孩子解题,又能让孩子在想象的基础上将所想表达出来。有了这样的成功体验,相信学生会更愿意画图。
二、联结迁移:降低空间观念发展的难度
苏教版教材注重对各个板块内容之间的衔接,各个知识点前后都有关联。如果将看起来分散的知识点编织成一张知识网,形成知识的点上开放、线上关联、整体建构,可使儿童的思维向长度、深度和广度延展,那将大大降低空间发展观念的难度。
1.知识联结
在教学中,教师应引领儿童理清知识的来龙去脉,整体、系统、联系地把握知识的结构,达到同类知识在儿童知识体系中自然生长的状态。
比如,以《多边形的面积》教学为例,长方形、正方形、平行四边形、三角形、梯形等平面图形的公式,如果将它们看作独立内容,那么学生要记忆的是五个又难记又易混淆的公式,这对本就有记忆障碍的孩子来说无疑雪上加霜。其实它们看似独立实则关联。
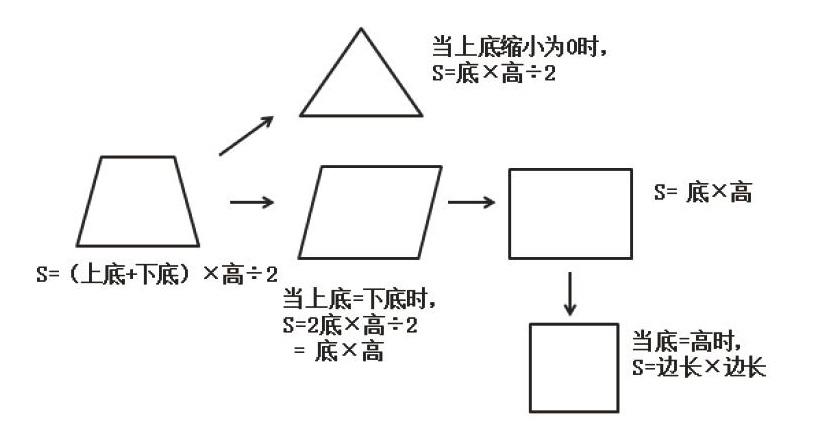
如果以梯形的面积计算公式为中心,向外发散:把梯形的上底缩小为0,成为一个三角形,三角形的面积=底×高÷2;如果上下底变成一样长,就变成了平行四边形或长方形,平行四边形(长方形)=底×高;如果将底和高变成一样长,就是一个正方形,正方形面积=边长×边长。如此,一个公式关联着四个公式,降低了记忆难度,也能让学生知道图形之间的关系。
看来,知识联结可以化多为少,化繁为简,降低空间观念的发展难度。
2.方法联结
在知识学习过程中,方法迁移能正向指引学生在遇到新问题时的思考方向。
比如,在“图形和几何”这一部分内容中,“转化”策略贯穿前后,不管是推导平面图形的面积:平行四边形转化成长方形、三角形(梯形)转化成平行四边形、圆转化成长方形……还是推导立体图形的体积:圆柱转化成长方体……都会发现是“转化”这种思想起着链接的桥梁作用。
在教学中经常会发现,只要题目稍稍一变,有的学生就不会做了,究其原因就是思维的断链:就题论题,没有想到题目不同,但思想方法是相通的。看来,小学数学教学中思想方法的渗透是必然与要求,提炼和感悟数学思想方法是发展空间观念的精神桥梁。
总之,空间观念的培养和提高,不是“一朝一夕,一招一式”之事。在教学中,我们应根据教学目标、教学内容合理选择教学手段和方法,更有效地促进学生数学素养的发展。

