例谈如何设计具有思考性的计算试题

曾荣章

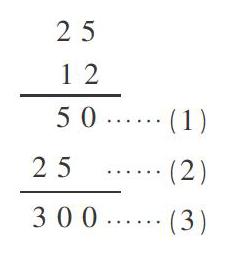
测试作为对学生学习数学和发展状况评价的一种工具，命题应该立足于对学生“过程性”思考的考查，试题素材应该注重考查学生运用所学知识技能来解决真实情景中的数学问题的综合能力。学生经历算理算法的认知过程，有助于促进其计算能力的提升。下面，笔者从六种计算试题的设计方法入手，介绍如何通过试题考查学生对计算的算法算理的过程性思考，促进学生在思考过程中进行知识建构。

一、设计“位值”试题，渗透数学思想方法

设计需要呈现计算思路、探究算理和算法过程的试题，应该从计算的深层次意义进行考查，根据位值原则让学生真正体会掌握每一步计算所表示的含义。

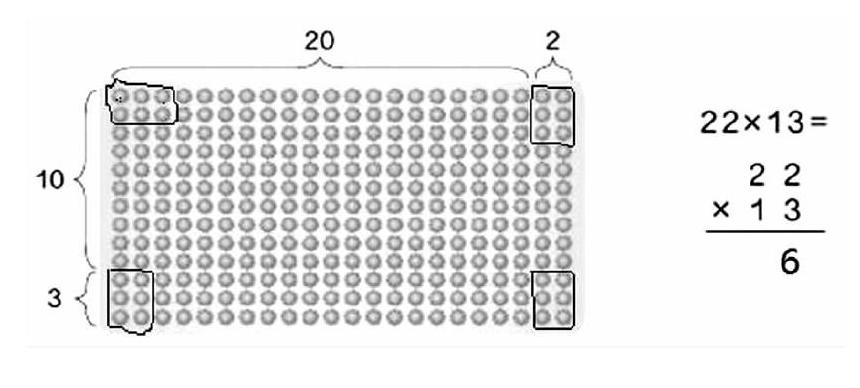
如下图，算式中的“6”在图中表示的位置在（  ）。

A. 左下角？摇？摇B. 右下角？摇？摇C. 左上角？摇？摇D. 右上角

本道题把两位数乘两位数的计算过程融入点子图，让学生发现竖式计算的每一步都可以用点子图表示出来，进而引导学生理解掌握每个位值的具体含义，体会到乘法算式的简捷有效，渗透数学思想方法。

二、设计“说理”试题，促进理解算理算法

设计“说理”练习让学生通过描述计算思路、表达算理和算法的过程探究策略，既培养了学生思维和表达能力，又促进学生应用所学知识站在新的高度去理解原来学过的算理算法。

一共有50个樱桃，陈希自己留下10个，剩下的分给3个小朋友，每个小朋友可以分到几个？陈希这样解答：50-10=40（个），40÷3=13. 33……（个）。

陈希想：按这样计算，每个小朋友分到的不是整数，要把自己留下的樱桃调整成多少个，才能使每个小朋友分到的樱桃变成整数，又与原来的数量最接近呢？请你帮陈希解决这个问题，写出思考过程。

以上设计的例题为学生呈现真实的生活问题情境，便于让学生读懂信息，找到数量关系来解决问题。通过让学生运用数学的知识说理，紧扣各种运算意义引导他们进行描述，大胆给学生“说理”的机会，让他们进一步理解并掌握算理算法。

三、设计“灵活”试题，培养多维思维能力

设计灵活性的计算题，学生要掌握运算法则、定律、公式等，然后在此基础上灵活运用解决问题。灵活性计算题主要考查学生计算方法的多样性、思维的灵活性。通过灵活性计算题的训练，可培养学生的发散思维意识和多角度解决问题的能力。

林老伯买了14个橘子共重2. 1千克，如果买这样的橘子13千克，大约有（  ）。

A. 200个以上  B. 不到50个  C. 80多个

本道题可以先计算每个橘子的质量，再用13千克除以每个橘子的质量，从而求出个数。也可以估计13千克大约是2. 1千克的6倍，个数大约就是14的6倍。此题通过引导学生从不同角度去观察同一个数学问题，使学生产生不同的体验，形成不同的解法。

四、设计“错误”试题，提升自我反思能力

小学生由于受到生理与心理发育水平的限制，缺乏精细理解和自我评价的能力，常有注意力不集中、解题粗枝大叶的习惯。如在计算36×8÷36×8时，由于该题的结构与36×8÷（36×8）相似，学生在计算时往往容易错误地算成288÷288=1。所以，教师可以通过设计“错误”练习，利用错误资源，让学生在反思中明确算理、修正错误、完善认知、突破难点。

小雨在计算一道除法算式时，不小心把被除数和除数末尾的两个0都去掉了，所得的商是9，余数是5，算式正确的商是（  ），余数是（  ）。

A. 9？摇？摇？摇？摇 B. 900？摇？摇？摇 C. 5？摇？摇？摇？摇 D. 500

本道题是在学生学习“商不变的性质”的基础上，深层次地引导在有余数的除法中如何巧妙地应用这一性质，学生能更有深度地感悟到被除数和除数同时除以100，商不变，余数跟着缩小到原来的的算理。

五、设计“情境”试题，提高解决问题能力

把计算教学融入现实生活情境中，有利于学生在解决问题的过程中掌握计算方法，形成技能。把计算和解决问题融为一体的试题，解决问题以计算为载体，感受“为什么这样计算”，计算以解决问题为目的，理解“怎样计算”，解决问题又以计算教学为媒介，提高解决问题的能力，以达到“以算促用，以算强用”的目的。

笑笑写作业时列了这样的算式“120-20×4”，下面哪个选项是这道算式求的问题。

A. 买一双120元的球鞋和4双单价为20元的袜子，一共花了多少钱？

B. 用120元去超市买东西，买了4双单价是20元的袜子，还剩多少钱？

C. 每双120元的球鞋和每双20元的袜子各买4双，一共花了多少钱？

D. 原价120元的球鞋降价20元后，买了4双花去多少钱？

通过创设生动的具体情境，让学生把计算方法应用到与自己生活实践紧密联系的真实情境中来，学生通过分析数量关系来真正理解四则运算的实际意义，从而培养学生用自己所学知识解决实际数学问题的技能。

六、設计“深刻”试题，挖掘学生潜在能力

教师教学的内容要触及学生的思维深处，以体现对学生的情感、态度和价值观的培养。通过设计隐藏丰富的，可以引发学生深度学习的数学知识的试题，让学生经历知识构建和方法迁移，可不断提升学生的思维水平，挖掘学生潜在的数学能力。

观察右面竖式，步骤（1）（2）（3）的计算思路是应用了（  ）。

A. 乘法交换律？摇？摇？摇？摇  B. 乘法结合律

C. 乘法分配律？摇？摇？摇？摇  D. 加法结合律

这道竖式，可以分解为25×12=25×（10+2）=25×10+25×2=250+50=300，试题把乘法分配律融进具体的竖式计算，让学生通过对每一个位值计算步骤的深层次思考，把每个步骤有机结合起来，完美地呈现出乘法竖式计算过程和结果中的深刻内涵。

总之，考查学生的计算能力，不仅要考查学生对计算基本方法、基本技能的掌握程度和计算结果的准确度，更重要的是要考查学生对算法算理的思考，从而让学生真正掌握计算所含的精髓，也让他们在思考的过程中进行知识的建构。

（作者单位：福建省云霄县下河中心小学？摇责任编辑：王振辉）