卷积神经网络数字识别系统的FPGA实现

孙敬成，王正彦，李增刚

青岛大学 电子信息学院，山东 青岛 266071

1 引言

卷积神经网络（Convolutional Neural Networks，CNN）是一类包含卷积计算且具有深度结构的前馈神经网络，是深度学习的代表算法之一[1]。近年来，卷积神经网络在多方向持续发力，已成为图像识别和语音分析领域中的研究热点[2]。相较BP神经网络结构，引入卷积层与混合层，降低了运算量。

手写数字识别是模式识别领域中热点问题，有着重要的理论价值[3]。识别过程首先通过网络反向传播训练样本数据，提取识别率较高的权重与偏置用于前向传播，通过计算带权输入与激活值，以输出层中激活值最大值所对应的位置表示识别值。训练样本数据来源于MNIST 数据库，数据库中为人工手写的0～9 的数字图片，包括50 000 训练样本和10 000 验证样本，灰度值于0～255之间，像素大小均为28×28[4]。尽管数字识别类别较小，但却有利于深入分析以及验证新结论，能够推广其他相关问题，一个直接应用即英文字母的识别。

2 卷积神经网络

神经网络的组成单位为神经元，神经元规则的连接形成网络[5]。BP神经网络连接方式为全连接，即相邻层神经元相互连接，使权重偏置数量大。而卷积神经网络则凭借卷积层的区域连接以及混合层的压缩，减少了参数数量，简化了网络结构[6]，使训练变的简单。但作为BP神经网络研究的产物，也保留部分特性，仍离不开带权输入(z)与激活值(a)的计算。公式如式（1）、（2）：

其中w为权重，b为偏置，l为当前层，j、k为神经元位置顺序，x表示输入神经元数据，σ为激活函数，激活函数选择Sigmoid 函数，其特性可将激活值压缩到（0，1）中[7]。

卷积神经网络结构主要由输入层、卷积层、混合层、全连接层、输出层五部分构成。采用了3 种基本概念：卷积核、局部感受野、混合层。卷积核由共享权重与偏置组成，对应不同的特征映射，用于卷积运算，考虑到FPGA资源，该系统选择一个卷积核。局部感受野与卷积核大小对应，表示区域性连接，区别于BP 的全连接。混合层，又称池化层[8]，可压缩数据内容，减小计算量。

传统网络结构如图1 所示。输入层输入图片像素数据；卷积层，令卷积核数目为3，分别与像素数据作卷积，得到3组数据；混合层压缩卷积层的输出，每2×2矩阵可用平均数或最大值表示。上述对于3 个卷积核的卷积、混合运算，利用硬件实现可同时完成，软件则需分3次计算，体现了硬件实现并行性的优点。之后两层均为全连接，全连接层需将3 组神经元矩阵转换为1 组列矩阵，以便于综合所有特征；最终计算输出层的激活值，最大值所在的位置即判别结果[9]。

图1 卷积神经网络结构图

参数设置如下所示。

输入层神经元数量：28×28

卷积核大小：5×5

卷积层输出：24×24（28−5+1）

混合层输出：12×12

全连接层神经元数量：100×1

输出层神经元数量：10×1

卷积神经网络一次完整的训练包括前向和反向传播。前向传播依靠权重与偏置计算带权输入和激活值，求得识别结果；反向传播推导和优化权重与偏置，以求高识别率。为使网络的输出能够拟合所有的训练输入，定义代价函数[10]，公式如式（3）：

式中，n为训练输入个数；y为标签值，a为输出层的激活值。反向传播的目的找到一系列让代价函数C尽可能小的权重与偏置，采取梯度下降法来达到目的[11]。梯度下降需要引入神经元误差，公式可表示为代价函数对带权输入的偏导，该过程存在激活函数导数。公式如式（4）：

权重与偏置的更新梯度可表示为神经元误差对该层w、b的偏导，公式如式（5）、（6）所示，由公式可得权重梯度可在偏置梯度基础上求得。以梯度下降法计算更新梯度，原数据与梯度对应相减，得到更新权重与偏置，反复训练，以求最高识别率：

3 前向传播实现方案

3.1 样本读取

网络前向传播输入层需读取图片像素，网络计算需读取权重与偏置。初始化均值为0，方差为1 的高斯分布网络权重与偏置。反向传播需读取标签值，标签值对应输入图像的值。训练过程小批量处理，即输入层一次训练输入MNIST 数据库中10 个样本，将样本像素数据输入到输入层神经元矩阵。

由于FPGA 不能够识别小数，所以，要经过浮点转定点处理，规定定点数位宽16 位，选择S3.12 进行转换。其中S表示符号位，3为整数位个数，12为小数位个数[12]。权重、偏置及标签值都应扩大4 095（位宽12 位）倍。以上均为有符号数。转换定点数后进行计算时，注意位宽的匹配。

3.2 激活函数的实现

Verilog 语言存在数学运算上的弊端，例如不能进行矩阵运算、不能够识别对数、更不能够计算导数等。为了设计的进行，对曲线函数采用分段拟合近似表示。通过分割将每段曲线近似为直线，将曲线线性化[13]。卷积神经网络用到激活函数及其导数，均可采用该方法处理。图2 为Sigmoid 激活函数在区间（−6，6）的图像，值域为（0，1），且单调递增。求解每段函数时，可以借助Matlab 基本拟合功能。激活函数求导过程类似，不作讲解。

图2 Sigmoid函数

令分割区间为0.5，并进行定点化，曲线代码如下：

上述代码将线性化函数的斜率、截距进行浮点转定点出理并以二进制数表示，因此横坐标也要做出相应调整。在（−6，6）两端，因变量结果趋近于0、1。代码中不再细分区间，直接令其值固定。将Sigmoid 函数及其导数作为底层，直接调用。

3.3 卷积层计算

如图3所示，输入层排列为28×28的神经元矩阵，卷积核大小为5×5，令跨度为1，卷积核与局部感受野对应乘加，最终与共享偏置求和得到带权输入z，经过激活函数得到激活值a，卷积后可得576 个神经元，维数转换后得下一层24×24的神经元矩阵。

图3 卷积计算结构

卷积过程重点即提取矩阵中局部感受野。提取方法可对矩阵首个元素进行控制，局部感受野其余元素均可导出。首元素移动，带动局部感受野移动。因此，仅控制a、b即可。由时钟控制a、b变化，直至扫描结束。

代码如下：

因此，一个时钟可得一组局部感受野，进而与卷积核进行卷积，最终求得带权输入与激活值，总耗时576个时钟周期，得到卷积层输出神经元。

3.4 混合计算

将卷积计算所得24×24 激活值矩阵划分2×2 小矩阵，并将矩阵中四个数据用平均值一个数据表示[14]，跨度为2，如图4 所示。提取2×2 矩阵与局部感受野方式相同，每一个时钟计算一组矩阵的平均值，耗时144 个时钟周期，得到下一层12×12神经元矩阵。该层不涉及权重与偏置，仅求激活值的平均数。

图4 混合运算结构

3.5 输出值计算

卷积神经网络混合层之后连接方式均为全连接，神经元排列由二维矩阵转为一维矩阵。如图5 所示，al-1表示混合层144 个神经元，与下一层的100 个神经元两两连接，求得带权输入与激活值；再与输出层10个神经元两两连接，计算求得输出值。每个连接对应一个权重，每个被连接神经元对应一个偏置，可见fully层权重、偏置个数为144×100、100；soft 层权重、偏置个数为100×10、10。

图5 全连接输出

该过程中，两层计算方式相同，以计算fully 层带权输入为例。Verilog 不能进行矩阵运算，根据矩阵定义，在for 循环中需对应好计算变量的位置。如图6 所示，x_pool表示混合层神经元，fully_w、fully_b表示该层权重、偏置，最终求得带权输afullyresult和激活值afullyresult，即图5中

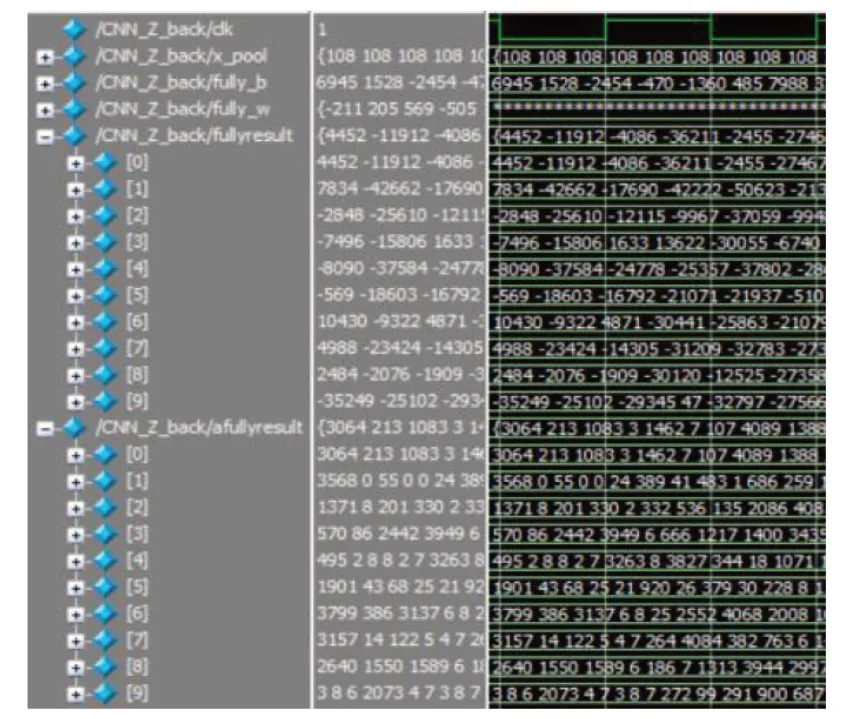
图6 fully层仿真

带权输入代码实现（fully层）：

输出层计算方式类似，100个激活值与10个神经元全连接，最终获得10个神经元激活值。加入比较器，比较激活值的大小，大小所对应的位置即检测样本数据。由于线性分割不够精确，激活值存在相等的情况，可根据激活函数单调递增特性，比较带权输入值即可。

3.6 小结

前向传播主要识别输入样本的值，即便采用一个卷积核，计算量仍较大，尤其在矩阵运算时，必须对应好相乘的量。Verilog语言实现特点就是加入了时序，例如卷积层计算应用576 时钟周期、混合层144 时钟周期等。总结前向传播电路结构，如图7所示，其中Sconv对应卷积层、fully对应全连接层、Soft对应输出层，给出每层的数据结构。由权重、偏置计算带权输入，并求得激活值（池化层除外），激活值作为为下一层的输入，经过混合层、输出层的计算，最终求得判别结果。

图7 前向传播电路结构图

4 反向传播实现方案

4.1 标签值读取

反向传播需读取标签值y，与输入样本类似，每个训练周期读取10个标签值。同样标签值需进行浮点转定点，因此列矩阵由0与4 095组成，标签值所在位置对应4 095。仿真结果如图8。

图8 标签值读取

4.2 权重与偏置的更新

权重与偏置共3 组，代码中分别表示为：con_w、core_b（输入层→卷积层），fully_w、fully_b（混合层→全连接层），soft_w、soft_b（全连接层→输出层）。更新梯度主要依靠公式计算，以下根据代价函数及神经元误差定义所做出的公式推导、实现方案。

公式如式（7），(a-y) 对应输出激活值与标签值的差，为 10×1 列矩阵；asoftresult'表示asoftresult对softresult的导数（激活函数的导数），得10×1列矩阵；两者点乘得到soft_b的更新梯度。

公式如式（8），包含soft_grad_b，为10×1 列矩阵，afullyresult激活值存于100×1列矩阵，两个矩阵相乘不能得到soft_grad_w的100×10 矩阵。因此根据公式进行计算不可行，需根据网络结构设定。令afullyresult的100×1 矩阵与soft_grad_b转置后得到的 1×10 矩阵相乘。因前向过程中，afullyresult中100个神经元与下一层10 个神经元连接；反向过程10 个神经元对应值为soft_grad_b。因此，afullyresult中每一个仍与soft_grad_b中10个计算，满足梯度对应关系。

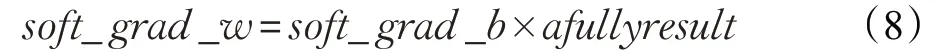
代码实现的关键即处理矩阵运算，必须要对应好因数位置[15]。全连接层梯度的推导方式大同小异，以权重更新梯度计算为例。

代码如下：

卷积神经网络一次训练十幅图片，目的是在更新梯度时，取平均得到较为准确的更新梯度[16]。以上代码即求得十组更新梯度。仿真结果如图9。all表示梯度和，ave表示平均值，即真正更新梯度。与原始数据求差，得到更新值。

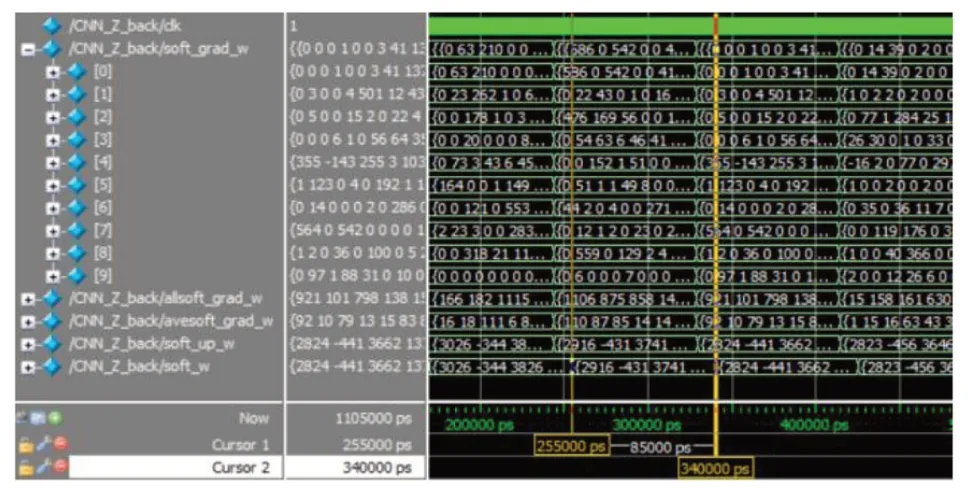
图9 soft_w更新仿真

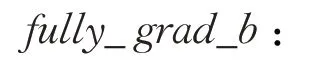
公式如式（9），soft_w为100 行10 列，此处不用更新值，矩阵乘积后得100×1矩阵，与afullyresult′（导数）作点乘。计算结束后求平均值得到100个fully_b的更新梯度。

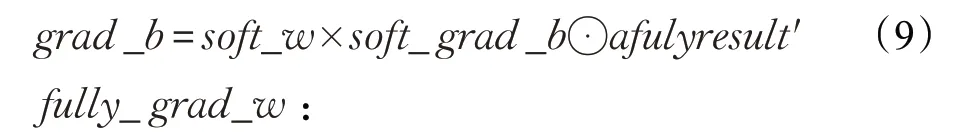
公式如式（10），结果是在fully_grad_b的100×1矩阵基础上与混合层x_pool的144×1矩阵进行乘积。同样矩阵要进行转置，换序，与计算soft_grad_w原理相同，最终得到144×100矩阵。

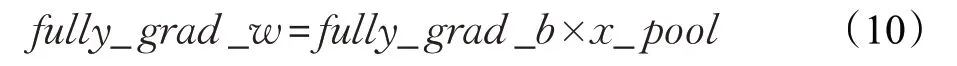
以上为以全连接方式连接的权重与偏置梯度的推导。卷积层计算方式与以上不同，但也离不开前一层神经元误差。

卷积层误差前向传播时，混合层将卷积层24×24神经元矩阵压缩为12×12。若要求得卷积层的误差，首先求得混合层误差，将混合层12×12 误差矩阵恢复至24×24神经元矩阵，处理称为Unsample[17]。混合计算利用平均值，展开过程将混合层的误差除以4，分布到每一个2×2的矩阵中。举例如图10所示。

图10 Unsample示例

卷积层与混合层之间不存在激活函数，x_pool即带权输入z，所以fullyresult对x_pool求导时结果为1，如公式（11）：

fully_grad_b为 100 行 1 列矩阵，fully_w为 144 行 100列，相乘得144 个神经元误差。进行unsample 处理，为了计算方便，将误差存入二维矩阵进行扩展，扩展结果即卷积层神经元误差。

共享权重与偏置数目较少，梯度推导方式也有所不同。25个权重梯度依靠输入图片像素与卷积层误差的卷积，即28×28矩阵卷积24×24矩阵，最终得到5×5的矩阵，对应共享权重的梯度，公式如式（12）；偏置梯度更为特殊，由于δ是高维张量，而core_b只是一个向量，通常的做法是将δ的各项分别求和，得到一个误差向量[18]，即为偏置更新梯度，公式如式（13）：

4.3 小结

反向传播通过更新权重与偏置，使代价函数降到最低，以求最大识别率。主要工作为公式计算，难点在于对梯度下降法的原理、公式推导的理解；利用Verilog代码实现，难点在于解决矩阵的运算、激活函数求导。该过程同样以时序控制，总结反向传播电路结构，如图11所示，权重、偏置梯度倒序计算，各层数据结构如图。矩阵相乘、转置对应4.2节中的公式计算，可以看出前两层的计算方式相同，计算输入为带权输入、激活值以及原始权重，输出为更新梯度。卷积层则依靠卷积、叠加计算方式求得更新梯度。提取全部更新梯度与原数据作差，求得更新值。该结构可由一条总线连接，是因为后一层的梯度由前一层梯度求得，公式中可以体现。

图11 反向传播电路结构图

5 网络的循环与实现

卷积神经网络一次完整的训练为10 幅图片，实际应用中需要训练MNIST 数据库中所有图片，因此在时钟控制下，网络的训练持续进行。一次训练的周期约为850个时钟周期，以时钟控制，每850个时钟周期输入新的训练样本，并更新权重与偏置。如图12所示，每个周期的训练，仅需要上次更新的权重与偏置，因此，在提取出新的权重与偏置后，可认为周期训练单独运行，互不影响。以计算fullyresult为例，如图13所示，每850周期计算一组。

图12 网络时序结构图

图13 fullyresult运算仿真结果

6 RTL级电路设计

在行为级描述及仿真正确的基础上，进一步进行RTL 级设计，以便进行硬件测试，该设计针对Altera 芯片Cyclone®IV 4CE115 及友晶开发板DE2-115。考虑到芯片资源有限，将卷积神经网络结构进行修改，卷积核由5×5 修改为3×3，全连接层由100 个神经元修改为30个神经元，小批量数据选择3个样本。训练系统框图如图14所示。

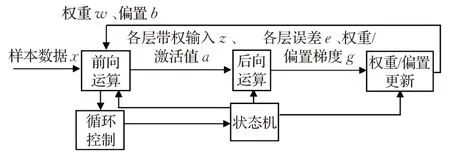
图14 卷积神经网络训练系统框图

样本数据经前向运算、后向运算后获得权重梯度和偏置梯度，然后进行权重、偏置更新，根据更新后的权重偏置继续对新的样本进行训练，反复循环进行。同时计算识别准确率，当准确率达到设置的阈值时，停止训练。由状态机控制各个运算过程的进行，当准确率达到设置阈值时，状态机停止运行。

由于样本数据需要输入电路进行处理，故采用双口RAM 存取样本[19]。权重和偏置需要更新处理，也采用RAM 存取。经过详细分析处理过程，将一次训练过程分解为7个状态。

S0：空闲状态。

S1：卷积运算，求卷积层带权输入；输入新样本（乒乓输入）。

S2：池化运算，求池化层激活函数；求全链接层带权输入/激活值。

S3：输出层带权输入/激活值；判决输出；计算准确率；求输出层误差；输出层偏置梯度；更新输出层偏置梯度。

S4：求全链接层误差、全链接层偏置梯度；更新全连接层偏置。

S5：求全连接层权重梯度；更新全连接层权重；求池化层误差；卷积层误差，卷积层偏置梯度；更新卷积层偏置。

S6：求卷积层权重梯度；更新卷积层权重。

S7：停止状态。

时序图如图15。其中卷积层的卷积运算及卷积层的权重梯度需要时间最长。

图15 训练电路时序图

根据时序分析，进行状态机设计。状态机的状态转换图如图16 所示。S7 状态即正确率达到设定阈值，停止训练，此时保留权重与偏置，直接用于识别数字即可。

图16 状态机状态转换图

7 结果与总结

7.1 行为级描述仿真结果

构造卷积神经网络，用于手写数字的训练与识别。利用quartus II编写 Verilog代码并进行编译综合，同时调用ModelSim 软件进行仿真，仿真结果如图17 所示，compare 表示样本标签，max_addr 表示识别值，right 表示正确识别的个数，count 为表示训练的总样本数计算准确率，统计结果如表1。当样本数目为20 000时，准确率达到最大值95.4%，继续训练识别率降低。分析原因，当参量、类别过于复杂时，神经网络训练时的收敛压力则越大，效果降低。因此，合适的网络参量数目是卷积神经网络达到良好实验结果的必要条件[20]。

图17 行为级训练结果

卷积神经网络训练60 000样本，将代码下载至工作频率可达 100 MHz 的 FPGA 中，训练耗时约 50 ms，而python训练耗时约8 min。因此速度显著提高。对于硬件描述语言在数学计算上的缺点，也得到了良好解决。即便存在浮点转定点、激活值计算所造成的误差，也并不影响识别结果。因此，以硬件实现卷积神经网络，保证了实时性、高准确性。

表1 识别率统计结果

7.2 RTL设计结果

在Quartus II 13.0 中对RTL 级前向电路进行了全编译及硬件测试，选取训练好的权重和偏置，电路可正确识别样本数据。网络结构在Quartus II 13.0 中进行了逻辑综合，并利用Modelsim-ASE进行了仿真，正确率可达96%。该设计基于Intel 公司的Cyclone IV 系列FPGA 芯片EP4CE115F29C7N 进行了验证，并在DE2-115 开发板上进行了硬件测试，输入样本数字进行识别测试，随机选取样本库中数据，灰度值排列如图18 所示，连接数码管引脚，直接显示识别结果，完成数字识别，结果正确如图19 所示。该设计可直接用于小型嵌入式系统进行数字识别。

图18 数字样本

图19 识别结果

8 结束语

本文以硬件描述语言（Verilog）实现卷积神经网络，并以手写数字识别为测试应用。相较软件实现而言，在保证准确率的情况下，满足了实时性的要求。尽管硬件描述语言在数学计算上存在缺点，但也得到了很好的解决。实现过程存在浮点转定点、激活值计算、求导所造成的误差，对识别结果影响较小。卷积神经网络作为图像识别的重要工具，要保证识别率足够高，才可真正应用于嵌入式设备，后续工作还需深入研究，例如增加网络层数将准确率再度提高或者实现其他识别应用等。