面向RDF图的多模式匹配方法

孙云浩，李逢雨，李冠宇，韩 冰，邢维康

大连海事大学 信息科学技术学院，辽宁 大连 116026

1 引言

在语义网中，资源描述框架[1]（Resource Description Framework，RDF）是一种基于图的数据模型，用于Web端的信息共享。给定一个数据图G和一个模式图Q，模式匹配（子图同构）问题是指搜索数据图G 中所有同构于模式图Q 的数据子图。多模式匹配问题是对模式匹配问题的一种扩展，其主要的挑战是多个模式图之间的并行策略。为了提高匹配执行效率：一方面，对于存在包含关系的多个模式图，需要避免对公共查询子图的重复计算；另一方面，在匹配执行过程中，尽量减少候选数据子图的量。因此，本文提出一种面向RDF 图的快速多模式匹配方法。

模式匹配问题是一种子图同构问题。子图同构问题是一种典型的NP 完全问题，随着数据图规模的不断增大，匹配的时间效率呈指数级变化。在面向RDF 图匹配处理中，大部分的研究者将RDF 数据存储到关系表中。Hexastore 采用一种基于索引的解决方案，将RDF 数据直接存储在B+树[2]。SW-Store 通过模式集合中的常量标签将RDF数据存储到一系列的垂直分片表中[3]，然后，通过构建关系表的索引快速地定位到需求的表。Jena 和Sesame 是基于图数据库的思想[4-5]，其抽离出RDF数据的概念构成属性表。基于关系表的研究者采用了相似的匹配策略。首先，其通过模式集合的有界标签来缩减对数据关系表的搜索空间；其次，过滤表中不需要的RDF数据，以便于达到对局部结果的存储，降低匹配处理过程的执行代价；最后，对局部结果进行连接运算，最终形成匹配的子图集合。然而，由于RDF数据的索引构建和预处理会有大量的时间消耗，因此，对于RDF数据的匹配处理具有相当大的延迟。

面向一般图的子图同构算法主要分为三类，基于树搜索[6-7]、基于约束传播[8-9]和基于图索引[10-11]的子图同构算法。其中，基于图索引的子图同构算法与基于关系表的模式匹配算法类似，通过构建图索引，减少搜索空间，快速搜索到模式图的匹配子图。然而，这种方法需要对整个数据集进行全存储，从而导致大量的时间消耗和存储代价。基于树搜索的子图同构算法利用可行性规则对一个树型搜索空间中不需要的候选集进行裁剪，以达到快速匹配的目的。基于约束传播的子图同构算法是将子图同构问题同构于约束传播问题，其目的是找寻那些分配到满足共同约束的变量集中的值。其主要的思想是基于局部约束的传播特性，节点或者边的一致性会传播到图中的其他部分。因此，在图中只有很少的候选集被保留。

多模式匹配问题是对模式匹配的一种扩展，其主要的挑战是多个模式图之间的并行执行策略。多模式匹配处理过程主要包括多模式图匹配序列优化和匹配策略。多模式图匹配序列优化一般通过计算多个模式图之间的包含关系构建多模式图的依赖图或者依赖树。文献[12]通过计算多个模式图之间的包含关系，生成最小依赖树，并利用依赖树的执行序列进行多模式匹配，一定程度上减少了候选集规模。文献[13]提出多模式图的依赖图构建和优化方法，其通过一个启发式算法制定模式图执行序列，减少了冗余计算以及候选集缓存。多模式图匹配策略主要的挑战是候选集的计算代价。文献[14]提出一个动态解决方法。该方法能够避免形成冗余候选集，并且可以在形成最大候选集之前到达结果集。文献[15]提出一种最大公共子图的优化算法，通过代价模型计算确保匹配代价最小。文献[16]通过提出的三元节点标签序列计算分组因子，从而得到模式包含映射，通过模式包含映射得到模式执行序列。

本文提出一种面向RDF 图的快速多模式匹配算法。首先，在D-Tree 构建算法中加入剪枝策略，通过剪枝策略使得构建的D-Tree最优。其次，提出节点分片表的概念。为了编排多个模式图之间的执行序列，构建了一种多模式图的依赖树。然而，包含关系是一种单一、抽象的表示，它不足以表示多个查询节点间的交叉关系。因此，提出了一个NFT的概念，用来表示节点间的执行关系。最后，提出一个基于D-Tree 和NFT 的多模式匹配算法，通过遍历一次RDF 数据图就可以得到多个模式图匹配的数据子图。当然，本文方法同样适用其他的所有有标签、无标签的图结构，对于无标签的图，可以对其定点和边进行唯一标识。如通过统一字典编码技术对属性图编码等。

2 依赖树和节点分片表

2.1 问题定义

定义1（基本模式图）一个基本模式图p(Vp,Ep,Lp,ϕp,varp)是一个有向标签图，其中Vp表示节点集；Ep表示有向边集；是一个有向函数，表示从u到v的一条有向边，其中u,v∈Vp；Lp表示边和节点标签集；varp表示一个标签变量集；表示一个将节点和边映射到对应标签的标签函数。在一个模式集中，不存在任意一个模式图同构于模式p，则p为基本图模式。

定义2（数据图）一个数据图是一个有向标签图，其中Vd表示节点集；Ed表示多个有向边集；是一个有向函数，表示从u到v的一条有向边，其中u,v∈Vd；Ld表示边和节点标签集；ϕd:Vd⋃Ed→Ld表示一个将节点和边映射到对应标签的标签函数。

基本模式图与数据图区别在基本模式图的标签可以为变量，变量标签指的是常量标签的一个集合，也可以称为标签的值域。因此，给定一个常量标签c和一个变量标签v，如果c是v值域内的一个常量，那么c∈v。

定义3（子图同构）给定一个基本模式图p(Vp,Ep,Lp,ϕp,varp)和一个数据图当且仅当存在一个双射函数f:Vp→Vd满足：

子图同构处理方法是找寻所有满足子图同构的节点对。给定一个基本模式图中节点vp和数据图中的节点vd，如果f(vp)=vd并且满足定义3中（1）和（2），那么搜索到的节点对为(vp,vd)。多模式匹配问题是对模式匹配的一个扩展，其侧重于多个模式图之间的并行执行策略。因此，避免多个模式图之间的重复计算问题是本文研究的重点。

定义4（多模式匹配问题）给定一个基本模式图集和一个数据图d，m∈N+。给定任意的一个基本模式图p∈P，多模式匹配指的是依次地搜索d中同构于p所有匹配的数据子图。

图1 描述的是多个模式图以及它们之间的公共子图。图（a）表示多个基本模式图，图中符号分别表示顶点和边的标签，“？”表示当前标签为变量。任意一个基本模式图都不同构于其他的基本模式图。图（b）表示多个基本模式图的公共子图，其中p6为模式图p1、p2、p4和p5的公共子图。

图1 基本模式图及其公共子图

2.2 依赖树

依赖树的构建能够清晰地描绘出多个基本模式图之间的依赖关系。大部分研究者通过计算多个基本模式图之间的公共查询子图，依靠基本模式图与公共查询子图的包含关系构建依赖树和依赖图。然而，并不是所有的公共查询子图都要构建到最终的依赖树或者依赖图中的，因为公共查询子图可能存在重叠的部分或者多个公共查询子图依赖一个相同的基本模式图集。因此，提出一种公共子图的裁剪策略。

依赖树的构建过程主要包括依赖图的生成和生成树的构建。依赖图的生成是通过计算多个基本模式图之间的公共查询子图，依靠基本模式图与公共查询子图的包含关系构建依赖图，生成树的构建是通过代价评估模型对依赖图的剪枝操作，为了能够清晰地表述出代价评估模式，给出了残差图的定义。

定义5（残差图）给定两个模式图pa和pb，并且pa子图同构于pb，那么pb相对于pa的残差图为pb-pa，包含pb中除去子图同构于pa部分后剩余部分的节点和边。这些顶点和边被称之为残差点和残差边。依赖树索引构建过程分为以下几步：

（1）依赖图生成（算法1，2～9 行），目的是找到模式间的包含关系。首先采用子图同构算法找寻多个基本模式图的子图同构关系，若存在子图同构关系，则构造它们之间的依赖关系。若不存在子图同构关系，则计算多个基本模式图之间的公共查询子图，然后构造基本模式图与公共查询子图之间的依赖关系。

图1 所示的模式图集构建的依赖图如图2（a）所示。依赖图为一个有向图，图中每条边连接的两个节点间具有子图同构关系，如p1子图同构于p4。图（a）中，p6也子图同构于p4，但是由于p6通过p1连接到p4，因此省略p6指向p4的边。图中实线节点表示模式集中存在的节点，虚线节点表示加入到模式集中的最大公共子图。

图2 依赖树构建过程

算法1 BuildDTree(P,∂)

Input：pattern graph setP={p1,p2,…,pn}，user specified parameter for VFT building

Output：D-Tree

1.InitialT=∅

2.for each petternpiinPdo

3. for each patternpjinPdo

4.if（SubgraphIsomorphism(pi,pj)）then

7. end if

8. end for

9.end for

10.CutRedundantEdge(T)

11.ReturnT

依赖图构建时间复杂度为O(N2)，N为模式图的个数。

（2）代价评估模型，目的是对依赖图的冗余节点和边进行裁剪操作。根据定义5，生成树的代价函数表示为：

其中，eij为基本模式图pi到pj的一条有向边和表示中节点和边的数量。∂为人为给定的参数。通过公式（1），可以为每条边赋予一个代价，表示基于pi的匹配结果执行pj匹配的代价。为了对节点进行评估，本文设计了一个权重函数，对虚线节点代价评估。权重函数构建为：

定义6（可裁剪节点）给定虚线节点pi，若其满足以下条件：①；②，则称其为可裁剪节点。其中，parent[pj]表示pj的父亲节点。

例1（可裁剪节点举例）如图2 所示，节点p6有两个孩子节点分别为p1、p2，p1有两个父亲节点分别为p6、p7，p2有两个父亲节点分别为p6、p8，因此p6满足定义6 中两条约束为可裁剪节点，在其同一层次中p7、p8也为可裁剪节点。

（3）依赖树构建，目的是为了最小化整体的匹配代价，减少重复计算。这一步对依赖图进行节点和边的裁剪，裁剪后的依赖图称为依赖树。裁剪节点时，由于虚线节点不需要结果集的输出，因此只对虚线节点及其相连的边进行裁剪。由出度为零的节点出发向上遍历，若某个节点为可裁剪节点，且同层次（从根节点向下遍历路径长度相同的节点为同一层次）上有多个可裁剪节点时，比较这些节点的权重，将权重最大的节点裁剪掉，直到这一层无可裁剪节点为止。重复此裁剪过程，直到依赖图中不存在可裁剪节点，则停止裁剪。图2（a）中可裁剪节点为p6、p7、p8，设 ∂=0.5，则分别为4.5、3.5、5，p8权重最大，将p8及其相连节点裁剪，此时p6、p7不再是可裁剪节点，且同层以及依赖图都无可裁剪节点，则停止裁剪，得到图2（b）。裁剪边时，使用最小生成树算法，对于每个节点只保留代价最小的入度边，以此保证每个节点只有一个父节点。裁剪边后得到图2（c）。时间复杂度为O(N)，N为模式图的个数。

依赖树的存储引入了模式边表（图3）的形式。模式边表（PE 表）分为三列，第一列表示所有依赖树中的节点（基本模式图或者公共模式图），第二列表示第一列中节点的父节点，第三列表示第一列中节点与第二列中父节点的残差边。

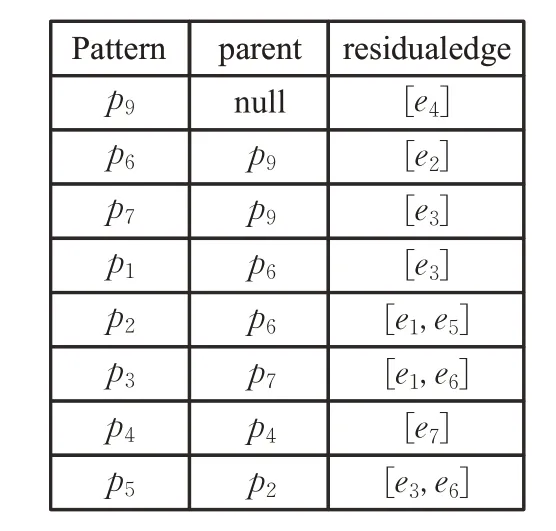
图3 模式边表

2.3 节点分片表

依赖树是对多个基本模式图之间依赖关系的一种描述。这种依赖关系可以以理解为对残差边的抽象。通过这些依赖关系可以有效地制定多个基本模式图之间的执行序列。然而，很难在这些单一的，抽象的依赖关系中发掘出有助于匹配效率的辅助信息。因此，提出了一个可以细化、实例化依赖关系的节点分片表。首先，给出了内部边和外部边的定义。

定义7（内部边和外部边）由D-Tree根节点依次向下遍历，给定两个模式图p1、p2，p1∈D-Tree，p2∈D-Tree且。存在节点，且存在节点，，边e(u,v)为节点u、v的内部边，记为i-edge。存在节点，且存在节点则为节点u的外部边，节点w的内部边，记为o-edge。

NFT由内部节点片表（简写为iNFT）和外部节点分片表（简写为oNFT）组成，其中包含内部边的为iNFT和包含外部边的为oNFT。NFT 包含两列：节点和边。在NFT 每行中，节点列只存放一个节点v，边列存放与v节点相连的内部或外部边，因此iNFT和oNFT被形式化为和

NFT 是基于D-Tree 构建的（算法2、算法3）。在DTree 中，由于没有其他节点同构于根节点，因此根节点的节点和边被直接存入iNFT 中（算法3 的5、6 行）。给定一个节点p1（不是根节点），它的父亲节点p2和一个节 点u∈Vp2，存 在 节 点v∈Vp1，使 得e(u,v)∈Ep1，，则为u的外部边，v的内部边。u和被存入oNFT（算法3的8、9行），v和e(u,v)被存入iNFT。算法伪代码如下：

算法2 NFT(P,∂)

Input：pattern graph setP={p1,p2,…,pn}，user specified parameter for NFT building

Output：NFT={nft1,nft2,…,nftn}

1.Initial NFT=∅

2.T=BuildPatternTree(P,∂)

3.P← {b|a=root，child[a]}

4.for each patternpinPdo

5.nft←sub-NFT(p,T,NFT)

6. NFT←NFT ∪nft

7.end for

8.return NFT

例2（NFT 构建过程举例） 图 2 为 D-Tree 构建的构建过程，图4表示的是NFT表。p9：由于p9为根节点，p9中节点？B、？D以及边e4被存入iNFT中。p6：对于p9中节点 ？B，在p6中存在节点？E，使得e2={?B,，因此e2为节点？B的外部边；对于p6中节点？E，在p6中存在节点？B，使得，因此e2为节点？E的内部边。

图4 节点分片表

3 多模式匹配算法

描述多模式匹配算法前，首先给定基本模式图与数据图之间的节点关系。给定数据图中的任意节点vd，模式图中存在节点vp与vd匹配，则vd是vp的一个实例，被表示为节点对(vp,vd)。给定数据图的任意两个节点，模式图中存在节点，满足的一个实例，的一个实例，且的一个三元组实例。

算法3 sub-NFT(P,T,NFT)

Input:pattern graph setP，PatternTreeT，NFT

Output：NFT

1.Initial NFT=∅

2.for each patternpinPdo

3. for eachvin patternpdo

4. ifv∄NFT then

5.E(v)={e|eu,v,u∈V(v)} is i-edge

6. iNFT (v)←E(v)∪iNFT(v)

7. else

8.E(v)={e|eu,v,u∈V(v)}-iNFT(v) is o-edge

9. oNFT (v)←E(v)∪oNFT(v)

10. end if

11. end for

12. if child[p]≠∅ then

13.P=child[p]

14. sub-NFT(P,T,NFT)

15. end if

16.end for

17.return NFT

多模式匹配算法基于D-Tree和NFT，多模式匹配结果是通过先序遍历D-Tree 逐步得到的。得到根节点proot的结果集分为以下几步：

（1）给定proot中的一个固定节点，在数据图中获得一个的实例节点vd，并且把它做为一个初始的数据节点。固定节点是由和D-Tree得到的。若节点为固定的，当且仅当固定节点由函数确定。

（2）顺序遍历vd的一阶邻居节点获得节点序，并设置为下一跳遍历的初始数据节点。下一跳遍历数据图时，给定一个初始数据节点和由它获得的节点，存在节点vp，满足是vp的一个实例且则被写入p9的结果集中。若，则被存入临时结果集Temp中。

算法4 Multi-pattern Matching(D,P,∂)

Input：pattern graph setP={p1,p2,…,pn} ，Data graph setD={d1,d2,…,dn}；user specified parameter for VFT building

Output：matching set ofp

1.Initialize Temp=∅ ，VFT=∅ ，set=∅

2.VFT，collectionlable=VFT(P,∂)

3.for eachdinDdo

4. get any nodev∈basicpattern ind

5. Temp←addnode(v,d,VFT,Temp)

6. While Temp≠∅ do

7. while Tempinnode≠∅do

8. TraverseInnerNode (Temp,NFT)//遍 历 内 部 节点，并存到Temp中

9. end while

10. ifTempinnode≠V（basicpattern） then

11. traverse the next data graph

12. end if

13. basicset←d∪ basicset

14. whileTempoutnode≠∅do

15. TraverseOuterNode（Temp，NFT）//遍历外部节点，并存到Temp中

16. end while

17. ifpiin collectionlable ∈Tempinnodethen

19. end if

21. end while

22.end for

23.return set

（3）执行proot匹配，直到没有新的三元组实例被加入到结果集中。

孩子节点结果集获得过程不同于根节点，需要通过父亲节点的结果集和临时结果集来获得，主要分为以下几步：

（1）将父亲节点的结果集复制到孩子节点中。

（2）给定孩子节点pchild的一个固定节点，在数据图中找到的一个实例节点vd，并把它做为临时结果集中的初始节点。若节点为固定的，当且仅当固定节点由函数确定。

（3）顺序遍历vd的一阶邻居节点获得临时结果集的节点序，并设置为下一跳遍历的初始数据节点。下一跳遍历临时结果集时，给定一个初始数据节点和由他获得的节点，存在模式节点vp，满足是vp的一个实例且，则被写入pchild的结果集中。在临时结果集上重复执行一跳遍历，直到没有新的三元组实例被添加到临时结果集中。

（4）将临时结果集上最终的初始化数据节点做为数据图上的初始数据节点，并执行（2）、（3）两步获得孩子节点结果集。

（5）重复执行（1）～（4）直到获得所有模式的结果集为止。

图5 面向RDF图多模式匹配过程

例3（面向RDF 图多模式匹配过程）多模式匹配过程如图5 所示。图（a）表示一个待匹配的数据图，图（b）、（c）表示D-Tree进行多模式匹配过程中结果集的变化，其中Result表示结果集，Temp表示临时结果集。

p9：由于p9是D-Tree的根节点，它的匹配过程只需要借助内部表。首先，，从?C、?D中任意选择一个节点做为固定模式节点。假设?B为固定模式节点，在数据图中b1为?B的实例节点，并把b1设置为一个（a）的初始数据节点。通过一跳遍历b1，三元组实例被写入p9的结果集中，三元组实例被写入临时结果集。之后，顺序的得到d1、d2并将它们设置为下一次遍历的初始节点。通过一跳遍历d1、d2，三元组实例被写入p9的结果集中，三元组实例被写入临时结果集中。

p6：p6的匹配过程需要借助内部表和外部表。由于p6为p9的父节点，把p9的结果复制到p6的结果集中。图5中由于图片大小问题，将不复制结果，只显示新遍历得到的结果。首先，由公式得到固定节点为?B，b1为?B的实例节点，并把b1设置为临时结果集的一个初始数据节点。通过一跳遍历b1，三元组实例被写入p6的结果集中，之后获得节点e1，由于e1在结果集中不存在，因此将其做为下一次遍历的初始节点。由于，三元组实例被写入p6的结果集中。至此，p6的结果集便得到了。其他模式的模式匹配过程与p6相似。通过M-PM 算法，通过遍历一次数据集便可得到所有模式图的结果集。

将本文多模式匹配算法分别与基本多模式匹配算法、文献[12]的多模式匹配算法以及文献[16]多模式优化算法进行比较。其中，基本多模式匹配思想是将DTree 中父节点的匹配结果集做为其孩子节点的输入的局部结果集，因此，它能够很好地降低父节点与孩子节点之间重叠部分的计算。假设模式图集大小为n，数据集数量（指三元组模式的数量）为m，基本多模式匹配的时间复杂度为。文献[12]中多模式匹配算法（MPT），分为基本模式匹配和扩展模式匹配两步，每次将基本模式的匹配结果集作为扩展模式匹配的输入，因此仍然有一部分数据图需要多次遍历，时间复杂度为，且其每次都需要对中间结果进行保存，大大增加了空间复杂度，其空间复杂度为。而此多模式匹配算法不需要对中间结果进行保存。文献[16]中多查询优化算法（MQO），通过模式包含映射确定一个多模式匹配序列，匹配时多个父模式的匹配结果集作为子模式的匹配数据集，因此时间复杂度为同时需要对中间结果进行缓存，空间复杂度为。本文多模式匹配算法的时间复杂度为因此本文的多模式匹配效率高于其他三个多模式匹配算法。

4 实验结果与分析

4.1 实验设置

基本模式图集。在选择模式集时，基本模式图之间的残差图是一个重要影响因素。在D-Tree 中，非叶节点的残差图与模式子图重叠部分相关联。D-Tree 的深度不断增加，越靠近根节点的模式图，匹配执行的次数越多。

数据集：实验中，选择一个仿真数据集。DBpedia 2015A描述了运动和运动事件的相关信息，它包含20个三元组模式的30 000多个RDF三元组实例。由于现有较大的真实数据集中三元组模式种类较少（如DBpedia、WikiData、YAGO），很难反映模式图残差边数量对多模式匹配效率的影响，因此，对三元组模式图进行了仿真扩展，用于提高三元组模式的维度，生成了一个基于DBpedia 2015A的仿真数据集，它包括300个三元组模式的300万个RDF三元组实例。

为了得出多模式匹配与D-Tree深度、宽度以及残差边数量之间的关系，同时为了更准确的进行实验，合成的数据集要符合现实世界中观察到的一般特征，如模式、结构、大小、分布等。在生成仿真数据集时，首先采用文献[17]中的方法对原始数据进行一定的扩展，为某些实例引入新的谓词，增加三元组模式的个数，同时删除某些三元组，这个过程生成了更加现实和复杂的数据集，增加了边的多样性，符合现实世界的现状和特征。

其次，采用一个随机生成器对上一步生成的数据集进行规模扩展。以数据图节点数N和最终数据集大小S作为输入，每次随机选择S/N个节点作为核心数据节点，对于每个核心数据节点v，选择10～15 个与v距离为5 跳的节点，并且用边将它们随机连接起来，重复多次，直到达到需要的数据大小。

实验配置：实验环境为Intel Xeon 5118，拥有24 GB RAM。

4.2 实验分析

在自己生成的仿真数据集上进行实验，分析D-Tree具有不同深度、宽度以及深度改变时的多模式匹配效率。

图6 描述具有相同深度不同宽度D-Tree 的执行时间，图7 描述具有相同宽度不同深度D-Tree 的执行时间。根节点包含80 个三元组模式，并且每个孩子节点比其父亲节点多10 条边。随着深度的增加，本文算法时间消耗与基本多模式匹配算法、MPT算法、MQO算法相比分别提高约70%、50%、30%的时间效率。由于子图同构是一个NP 完全问题，其随着数据的规模不断增加呈现指数级的时间复杂度，因此，在图6 和图7 中，随着深度和广度的增加，三元组模式的数量也在不断的增加。从线性的变化趋势中，可以发现其近似于指数型的变化，然而，由于三元组模式图的数量远远小于数据图数量，因此，实验线性的指数型变化不够明显。

图6 不同宽度D-Tree的执行时间

图7 不同深度D-Tree的执行时间

从图6和图7综合来看，当宽度和深度相同时，算法执行时间相同，因此算法的执行时间受深度和广度的影响相似。

采用相同数量的三元组模式和残差边，改变残差边在D-Tree中不同深度位置，执行时间如图8所示。随着D-Tree深度改变，深度越深，模式间残差边越少，本文算法比其他多模式匹配算法波动小，更加稳定。而其他算法随着深度的增加，执行的时间消耗呈现增大。因为，深度越高，公共部分的重复计算的次数越多，然而，其对本文算法的影响微乎其微。因此，本文算法仅与残差边的数量有关。

图8 模式图深度改变的执行时间

为增加实验的真实性和可靠性，在仿真数据集Wet-Div 上进行对比实验，如图9 所示。WatDiv 是一个关于电子商务的合成数据集，包括购买产品并撰写评论的用户，以及提供产品的零售商等。本文采用扩展因子为30，生成有300万个RDF三元组的数据集。

图9 仿真数据集WatDiv实验

为增加实验的真实性和可靠性，同样在真实数据集YAGO上进行对比实验（如图10），采用的数据集中包含900多万个三元组模式。

图10 真实数据集YAGO实验

由图9、10 在仿真数据集WatDiv 以及真实数据集YAGO上的实验可以看出，在仿真和真实数据集上本文算法同样优于其他算法，且算法时间复杂度只与残差边的多少有关，与D-Tree的深度、宽度无关，当深度改变时本文算法更加稳定。

5 结束语

本文提出了一种面向RDF 图的多模式匹配方法。为了表示模式间的依赖关系，减少重复计算，它构建了树形索引结构（依赖树），制定了模式间的执行序列。同时利用节点分片表，表示节点间的执行序列，根据节点序和模式序进行多模式匹配，进一步减少了重复计算，而且能在很大程度上提高模式匹配的效率。尽管此种算法很大的优点，但仍有许多可改进之处，故在今后的研究中会对此算法进行进一步的优化并增加真实数据的实验评估。