基于问题学习的数字图像均值滤波器教学研究

傅志中，李晓峰，周 宁，徐 进，何 翔

（电子科技大学通信与信息工程学院，成都611731）

0 引 言

“百闻不如一见”凸显了人类在生产和生活中对图像信息认知与获取的重要性。近年来，随着处理器计算能力的快速发展和机器学习等人工智能技术的进步，数字图像处理技术在工业、农业、国防和医疗等各个领域都得到了越来越广泛的应用，数字图像处理课程已经逐渐成为高校电子信息类专业的一门重要专业课程。

数字图像处理课程是一门涉及多学科交叉领域的综合课程，其理论性和实践性都较强。其中，图像滤波算法是一种广泛应用于数字图像处理的基本图像处理技术，在经典的图像数字图像处理教材［1-3］中都进行了详细的原理阐述。但是，限于教材的整体结构组织及教材的时效性特点，上述教材对于图像滤波算法的原理性阐述都是片段化、离散化的，没有及时吸收最新的图像滤波算法，没有从系统性的角度对图像滤波算法的发生、发展及其滤波算法之间的内在联系进行阐述。因此，尽管学生学习了各个滤波算法，但都不能对滤波算法有一个整体的认识和理解，缺乏理论联系实际的工程应用过程，导致学生在面对工程问题时，缺乏解决问题的创新性思维和方法。

韩智等［4］把基于项目学习的教学策略引入到数字图像处理的实验课教学中，以指纹图像的特征提取为例，引导学生将多个知识点进行有机联系，提高学生解决实际问题的能力。这种教学模式，需要学生已经学习或掌握相关知识点内容，不适合于初学者对图像处理算法的学习与理解。吴冬梅［5］将研究性教学引入到课堂教学中，对研究性教学的目的、课堂教学模式、教学内容设置和教学实施方式等多个方面都进行了较为详细的阐述，但是，该文没有详细的教学案例。张显斗等［6］在研究生数字图像处理课程教学中，探索了以拟讲授知识点的相关研究论文为导向的教学模式，实践了以一个完整的成像系统实验内容为依托的实验内容改革。这种探索，对于提高学生的工程认知与研究能力具有重要意义。陈青［7］探索了以学生已有知识为基础，采用启发式、探究式和研讨式等多种教学方法，提高学生的创新思维能力。盛敏［8］根据数字图像处理的多学科交叉特性，探索图像处理算法的来龙去脉，针对学生个体差异，实施分层教学方案，并将理论教学与实践教学紧密结合。实践表明，该教学方法能显著提高具有较好数学基础和较强计算机操作能力学生的学习效果。但是，这些教学模式，对于拟讲授的知识点而言，没有深入挖掘知识点之间的内在关联。吴兴华等［9］以突出算法的应用性能和特点，针对不同的图像噪声，分析了图像均值滤波、中值滤波、高斯滤波和频域滤波等多种滤波器原理，并根据其原理，以实际案例进行讲授。该教学方法对于学生理解不同滤波器原理具有重要意义，但是，由于该文讨论的滤波范围宽，因此没有给出不同滤波器之间的内在联系。

基于问题的学习方法［10-11］对学生创新实践能力培养的具有重要意义，刘春城等［12］从教学问题设计及问题库建设等方面进行了有益的探索，梁佩鹏等［13-14］将该方法引入到课堂与实验教学中，取得了良好的教学效果。以图像线性均值滤波算法为例，首先分析图像均值滤波器、高斯滤波器、双边滤波器［15］和非局部均值滤波器［16］的算法设计思想及其之间的内在联系。之后以问题为导向，逐步将不同应用环境中的图像滤波问题呈现给学生，引导学生运用已有知识、分析不同应用环境中面临的实际问题。通过该引导过程，培养学生从应用中提出问题、解决问题的工程素质，实现创新人才的培养。

1 教学内容

受零均值噪声污染的图像，根据随机信号分析理论，采用均值滤波器能有效抑制图像噪声、提高图像输出的信噪比。图像线性均值滤波可根据其滤波器特性，分为常规均值滤波［1］、高斯滤波［1］、双边滤波［15］和非局部均值滤波［16］等4类。

1.1 常规均值滤波原理

常规均值滤波算法，也称为邻域均值滤波法，是最基本和简单的一种图像滤波方法。设待滤波图像为｛Ip，p＝（i，j），i∈［1M］，j∈［1N］｝，其中M和N分别是图像的水平和垂直方向的像素数，Ip是图像在位于坐标p处的像素取值。δp是位于坐标p处像素的邻域坐标集合，也称为滤波模板。则邻域均值滤波算法为：

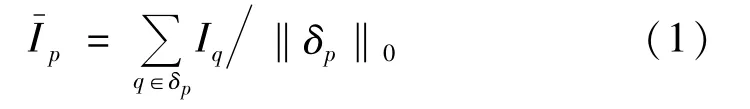
式中：‖δp‖0为δp的零范数，即邻域中的像素个数，也称为滤波模板尺寸；p为位于坐标p处滤波后的像素取值。模板尺寸对滤波的效果有显著的影响，需要根据图像特性选择合适的模板尺寸。邻域均值法在抑制噪声的同时，也会使图像变得模糊。模板尺寸越大，滤波后的图像就越模糊。模板的尺寸大小一般为奇数。

1.2 高斯滤波原理

如果噪声源是零均值高斯噪声类型，则最佳的噪声抑制滤波器是采用高斯滤波器。高斯滤波器的模型为：

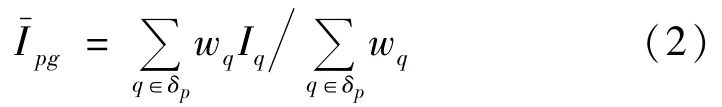
式中：wq为服从二维高斯分布的加权函数，Ipg为高斯滤波器输出结果。该模板取值由如下的高斯函数决定：

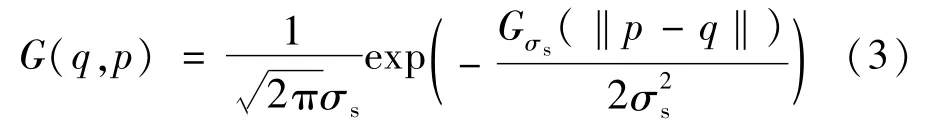
式中：Gσs（·）的定义与高斯滤波器类似；‖p-q‖为邻域δp内所有像素q与邻域中心像素p的距离；σs为高斯模板的标准差。标准差越小，二维高斯模板图像越小，平滑效果不明显；标准差越大，高斯模板图像越大，滤波效果比较明显。

1.3 双边滤波原理

应用均值滤波或高斯滤波对图像信号进行滤波时，图像信号必须是平稳的，否则图像的边缘将被模糊掉。为适应非平稳图像信号的噪声抑制，Tomasi［15］于1998年提出了双边滤波算法。该滤波器不仅考虑了图像像素空域位置之间的距离，还考虑了像素之间亮度或色彩差异，使得在有效滤除图像噪声的同时，保持图像边缘锐利特性。双边滤波器的模型为：

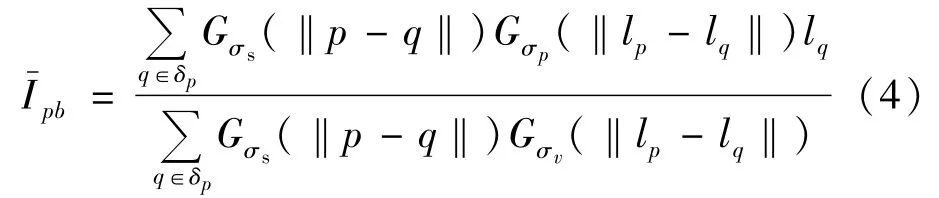
式中：Gσs（·）和Gσv（·）的定义与高斯滤波器类似；为双边滤波器输出结果。‖Ip-Iq‖为邻域δp内所有像素位置q的像素值与邻域中心像素位置p的像素值差异；σv为像素值差异高斯模板的标准差。类似高斯滤波器，标准差越小，二维高斯模板图像越小，平滑效果不明显；标准差越大，高斯模板图像越大，滤波效果比较明显。

1.4 非局部均值滤波原理

研究发现，图像信号的局部特征在空域具有重复特性，即图像中的任意一个像素位置的局部取值特性，在当前图像中的其他像素位置也会出现。基于图像像素的该特性，Buades等［16］提出了一种非局部均值滤波算法。即根据待滤波的像素位置的局部取值特性，根据一定的相似性准则，在整幅图像的其他像素位置，寻找具有相似特性的像素q，由于单个像素易受噪声影响，因此在计算相似性时，通常以像素的局部邻域特性来计算相似性。非局部均值滤波器的模型为：

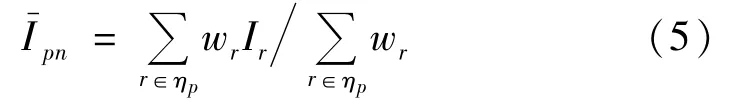
式中：ηp为根据相似性计算方法得到的相似性像素集合，r∈ηp，pn为非局部均值滤波器输出结果。计算两个像素相似性的最常用方法是计算其所在区域图像块的欧氏距离为：

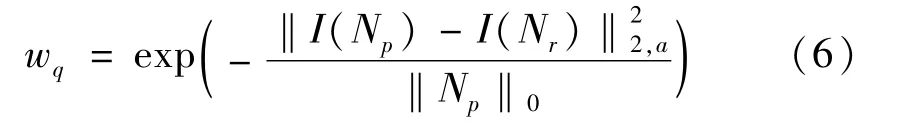
2 教学案例设计

从上述滤波器的原理描述可知，常规均值滤波、高斯滤波、双边滤波和非局部均值滤波等4类，都是针对零均值高斯噪声设计的滤波算法，对高斯噪声都有显著的噪声抑制作用。目前的教材和相关教学中，没有将这几种滤波器进行对比，学生在学习了这几种滤波器之后，不能深刻理解这几种滤波算法之间存在的紧密联系和差异，因而不能有效地激发学生的学习兴趣和创新思维及解决问题的能力。

（1）设计一幅同时有局部均值平稳和非平稳区域的棋盘格仿真图像，以案例方式，逐渐展开不同滤波算法的优缺点。以解决工程问题为导向，引导学生思考问题，解决问题。最后以实际图像滤波为例，进一步揭示仿真测试与实际工程应用之间存在的差异。从原理描述可知，常规均值滤波算法，对于图像局部均值平稳的图像信号，其滤波效果显著，能显著抑制噪声。但是，对于实际的图像信号，在图像平坦区域，其均值在小范围内存在均值平稳性。随着滤波器模板尺寸扩大，其均值是非平稳的。特别是位于图像边缘的像素，其相邻像素的统计均值是不平稳的。因此，高斯均值滤波算法，相对于常规均值滤波算法，对位于平坦区域的像素，具有更好的噪声抑制。双边滤波算法和非局部均值滤波算法能更好地适应均值非平稳的图像信号，特别是非局部均值滤波算法，能更好地抑制位于图像边缘处像素的噪声。

图1（a）所示是黑白相间的棋盘格，灰色区域部分的像素取值为0，白色区域部分的像素取值为1。在白色或灰色区域的各自区域内，所有像素的邻域均值是等同的，即均值是平稳的。但不同区域之间的像素的均值是非平稳的。图1（b）所示是均值为0，方差为0.001噪声污染图像，图1（c）所示是污染图像的局部放大图。

图1 黑白相间的棋盘格

首先应用常规均值滤波算法，滤波模板尺寸为3×3，对图1（c）进行滤波，其滤波图像如图2所示。

图2 常规均值滤波结果

图2（a）和（c）所示分别是3×3和7×7模板的常规均值滤波结果，图2（b）和（d）所示分别是图2（a）和（c）的局部区域放大结果。在局部放大图2（b）和（d）中，平滑区域的噪声都得到了明显的抑制，但噪声的影响还存在，同时，在两种平滑区域的交界处，边缘都因为模板的平滑作用而变得模糊。

针对此问题，教师要求学生自主提出解决方案。根据实验结果，学生能给出增大模板尺寸、实现平滑区域的噪声抑制的建议。但对于边缘平滑问题，未能给出有效建议。在给出高斯噪声在空间分布呈现中间高，边缘低的提示后，学生能给出采用高斯滤波的建议。

图3（a）、（b）和（c）所示分别是3 ×3、7 ×7 和15×15模板的高斯均值滤波结果的局部放大图。结果显示，高斯滤波相对于常规均值滤波能取得更好的噪声抑制效果，并且随着模板尺寸增加，噪声抑制效果更好，并且边缘模糊更低一些。但是，在两种平滑区域的交界处，边缘仍然因为高斯模板的平滑作用而变得模糊。

图3 高斯均值滤波结果

针对边缘仍然模糊的问题，教师与学生一起分析问题。指出，在平稳区域，上述滤波算法都能取得较好的噪声抑制效果，但在非平稳区域，噪声被抑制的同时，图像质量出现恶化。引导学生思考，是否可以对不同的区域，采用不同的方式来处理？基于该处理思想、给出了双边滤波算法的实现结果。

图4（a）和（b）所示分别是双边滤波结果及局部放大图像。图4（b）中，噪声被显著抑制的同时，图像的边缘也没有因为滤波而恶化，得到了良好的保持。至此，通过逐次展示各种滤波算法的实验结果，使得学生理解了不同滤波算法在图像噪声抑制中的特点及其关系。

图4 双边滤波结果

（2）设计了一个问题：针对高斯噪声，是否双边滤波就是最好的滤波器了？还有更好的滤波算法吗？针对上述的棋盘格仿真图像，学生对此展开讨论并指出双边滤波算法确实已经满足要求，应该能满足工程应用了。针对学生的讨论结果，教师随后给出了受高斯噪声污染的Lena图像。学生才发现，基于仿真图像得到的结论，还不能代表实际图像的测试结果。

针对此问题，教师给出提示，是否可以借鉴双边滤波算法的思想。滤波算法中，参与滤波的像素是否必须具有相同的特性。由于实际图像的复杂性，要求学生思考如何选择参与滤波的像素，以什么准则来选取性质相同的像素等问题。从而引出了非局部均值滤波算法原理。

以图5为示例，揭示非局部均值滤波思想。图中p为当前待滤波的像素，取p的一个矩形邻域δp，在整幅图像中，采用最小均方误差准则，搜索出与δp相似的像素点，如图所示的q1，q2，q33个像素点。之后，采用式（6）得到像素点p的滤波结果。

图5 非局部均值滤波算法相似性原理［16］

至此，通过仿真图像和实际图像的算法测试、问题分析及问题解决，引导学生完成了从理论仿真、算法分析至工程应用的整个过程，实现图像处理中创新思维的培养。

3 结 语

针对几种图像均值滤波器算法的内在逻辑关系和不同应用环境所面对的图像滤波问题，以解决工程问题为中心，引导学生运用已有知识，在案例中发现问题、解决问题，培养学生从工程应用中提出问题、解决问题的工程素质，实现创新人才的培养。