基于波浪衰减分析的快速率定造波方法

刘亚伊，陶爱峰，张海明，徐 伟，徐 啸，张珍瑶

（河海大学港口海岸与近海工程学院，海岸灾害及防护教育部重点实验室，南京210098）

0 引 言

波浪水槽实验是波浪有关科学研究与教学演示常采用的实验手段。受黏性耗散和边壁摩擦的影响，波浪在水槽内的传播过程中会产生能量衰减，波高会逐渐减小。为了使水槽实验段的波高满足需求，需要通过率定来控制造波板输入参数，而率定的过程往往只能靠经验和多次尝试。迄今为止，尚没有支撑率定过程快速准确开展的技术手段。

黏性耗散是波浪能量衰减的主要原因之一。水的黏性虽然很小，但在波浪作用下水的雷诺数达到某一临界值时，其流动即失去稳定性而产生紊动，从而损耗波浪的大量能量，引起波浪能量的衰减。赵子丹［1］基于微幅波理论分析了二维深水波浪的耗散衰减过程，但实验室中更多的是过渡水深情况，相应的衰减机理需要进一步探讨。程苏闽等［2-3］对黏性底层对波浪的能量耗散影响分别进行了理论推导与试验，得到了衰减系数随波浪频率的变化关系，但由于试验设备较为简单，结果精度有待提高。

文献［4-5］中基于高阶谱数值方法讨论了黏性耗散对调制波列不稳定演化的影响，主要考虑的是黏性衰减对波波相互作用的影响。孙哲［6］基于FLUENT建立黏性数值波浪水槽模拟了较大范围的规则波，发现波浪沿程衰减基本符合对数规律，但其测点较少且间隔较长，不能精确地测量波浪的沿程变化。赵艳等［7］通过模拟具有不同波长、波高的余弦波研究黏性在数值波浪水池中的影响，发现波高沿水池长度方向发生了明显的衰减，衰减幅度与波陡呈正比，衰减形式符合指数规律。尽管这些研究都从某种程度上解释了波浪的衰减规律，但并未给出一个显性的波浪衰减公式，不能直接应用到实验过程中。

除了黏性耗散外，水槽侧壁对波浪传播衰减也有一定影响，但相关研究较少，且大多集中于水槽底部边界层对衰减的影响［8-10］以及侧壁对结构物受波浪力的影响探讨［11-12］。文献［13-14］中分别从能量和压力做功两方面研究了波浪在水槽传播过程中的衰减规律，但其理论分析基于线性和层流假设，不能直接应用到更广泛的非线性波浪条件；秦崇仁［15］根据波能守恒原理研究了水槽侧壁摩阻对波浪衰减的影响，但其衰减系数计算公式较为复杂，波浪边界层流态难以精确测量。本文结合前人通过理论推导和数值模拟得出的波浪耗散衰减规律，通过多组次规则波试验，对波浪衰减影响因子进行分析，以得到更准确的波浪衰减公式，为波浪演变研究及实验室精准造波提供理论支撑。

1 实验装置及方法

1.1 造波水槽

实验在河海大学港口海岸与近海工程学院实验中心一个长70 m，宽0.5 m，高1.3 m的玻璃边壁平底矩形水槽内进行。水槽一端配备数字控制的液压伺服推板式造波机，另一端有斜坡消浪网，以减小反射波浪的影响。实验系统由推板式造波系统和数据采集系统两部分组成。实验中波面高度的测量采用南京水利科学研究院所研制的DJ800型多点测波系统，所有仪器均在实验中多次使用，性能可靠；在实验期间不定期做检测和率定，确保其正常运行。

1.2 波高仪布置

波高仪在造波机前5～35 m布设，共布置24根波高仪。波浪水槽及波高仪布设位置如图1所示。水深、周期和波高作为造波控制参数，波高仪采样频率均为50 Hz，当波浪传播到最后一根波高仪时开始采样，采样时长为100个波周期。

图1 实验装置及波高仪布设示意图（m）

1.3 实验参数及工况

影响波浪运动和变形的主要因素有水深、周期和波高等参数。本实验分别通过改变实验水深h、周期T和波高H的输入，共组合出43组实验工况来研究相对水深hk、波陡ak和厄赛尔数Ur等参数对波浪沿程衰减的影响。实验工况见表1，为确保实验的可重复性，实验中每种工况重复做3次，取3次的平均值进行数据分析。

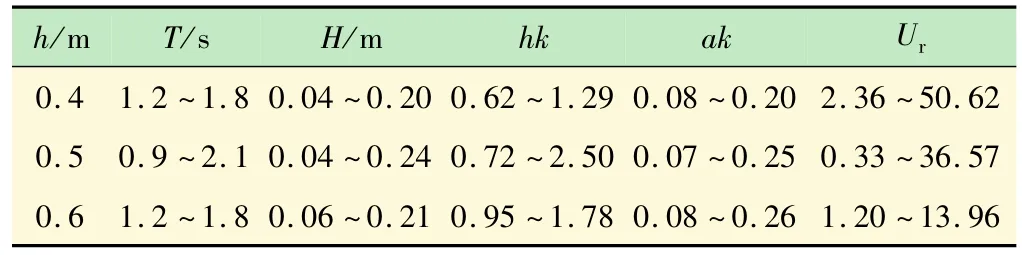
表1 实验工况组次

1.4 实验与分析过程

（1）设计好实验方案并确定实验工况，包括水深，周期和波高等波浪基本要素；

（2）架设波高仪等测量仪器，在造波系统输入波浪基本要素进行造波，采集所需的波浪数据；

（3）基于波高仪记录的波面过程，利用上跨零点法求得每根波高仪在稳定传播过程时无反射波浪的波高；

（4）对沿程波高进行指数拟合得到波浪衰减系数，并分析其与波浪基本要素的关系；

（5）根据衰减系数影响因素分析的结果，基于目标波浪要素计算需要输入造波系统的率定波浪要素并重新造波，实现在水槽中快速、精准地模拟目标波浪。

2 实验结果

2.1 波浪沿程衰减规律

通过上跨零点法可得到每根波高仪所测得的波高，以工况M501216 组次的第1、6、12、18、24 根波高仪为例，其波面过程η-t及所得波高如图2所示。由图2可知，每根波高仪所记录的波面是稳定传播的，但沿程5根波高仪记录波面所得波高不是固定不变的，在30 m距离的传播过程中波高存在近20%的衰减。

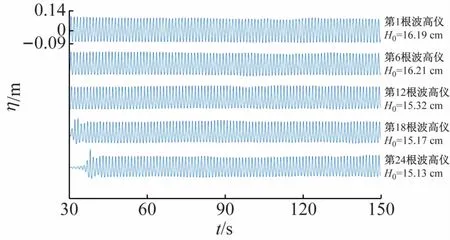
图2 不同波高仪所测波面过程

为研究波浪的沿程变化规律，将每根波高仪的波高按照其对应位置绘出波高沿程分布图，如图3所示，可以看出，距离造波板越远其波高的沿程衰减越小，大致符合负指数规律：

式中：Δx＝x-x0为波浪传播距离；H（x）和H（0）分别为x和x0处的波高值，此处x0为第1根波高仪的位置；δe为衰减系数。

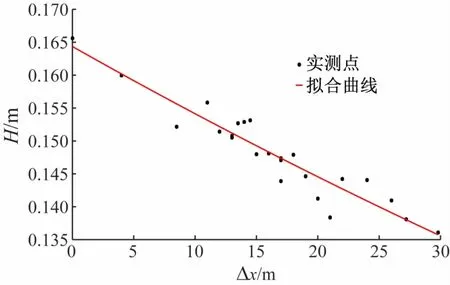
图3 24根波高仪所测波高沿程衰减规律

按照最小二乘法原则，对M501216组次沿程波高进行指数拟合的结果，δe＝0.006 4。由

计算得到残差平方和（SSE）为1.16×10-4，拟合结果较好。式中：n为数据总量；yi为实测值；y′i为拟合值。

2.2 衰减系数影响因素分析

为了探讨δe的影响因素，分别根据43组工况的实验结果讨论水深、周期和波高对衰减系数的影响。

M401212～M601812共9组工况的δe与水深h的关系如图4所示。由图可知：周期T和波高H不变时，δe与h呈正相关，即h越大，δe越大，沿程波高衰减越严重。由于水深变化，主要改变的是水槽侧边壁的影响，水深越大，水槽侧边壁淹没面积越大，摩擦耗散影响越大，说明水槽侧边壁确实会影响波浪衰减。

h＝0.5 m 时，M500909～M502118共22组工况的δe与T的关系如图5所示。由图可知：h和H不变，δe与T呈负相关，即周期T越小，δe越大，沿程波高衰减越严重。同时，由于h和H不变，波数k随着周期T增大而减小，说明波数k越大，衰减系数δe越大，这与Wu 等［5］的结论是一致的。

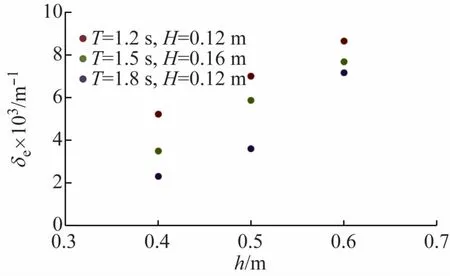
图4 衰减系数与水深的关系

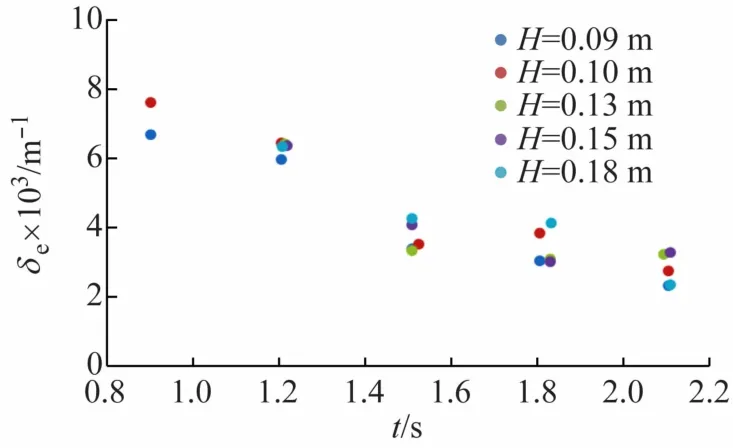
图5 衰减系数与周期的关系

h＝0.5 m 时，M500904～M502124共27组工况的δe与H的关系如图6所示。由图可知：h和T不变，δe与H成正相关，即波高H越大，衰减系数δe越大，沿程波高衰减越严重。同时，由于h和T不变，波陡ak随着H增大而增大，说明ak越大，δe越大，这与赵艳等［7］的结论是一致的。

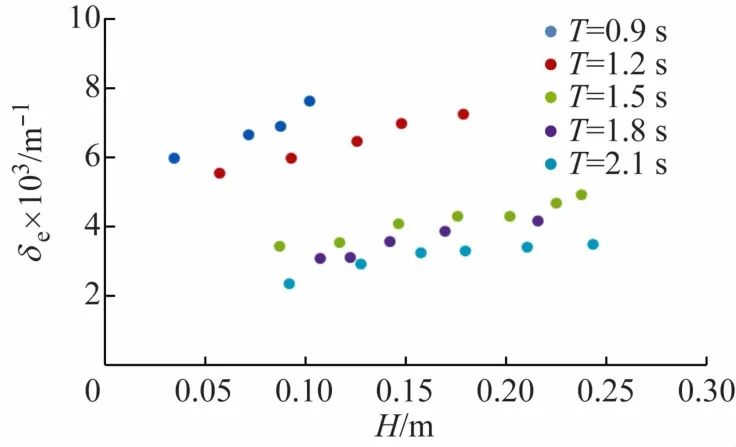
图6 衰减系数与波高的关系

2.3 厄赛尔数与衰减系数的关系

通过h、T和H3个基本波浪要素对δe的影响分析，发现三者均与δe存在一定的相关性，但三者又相互影响。综合考虑三者的多元函数作为率定波浪要素的计算公式，在公式拟合和实用价值方面都存在较大困难。为了进一步探讨过渡水深下三者对δe的共同影响，结合前人对波浪传播衰减的研究，本文考虑将厄赛尔数作为影响δe的综合指标。

厄赛尔数Ur来自非线性周期波的Stokes展开，是衡量波浪非线性强弱的一个无量纲参数，其定义如下：

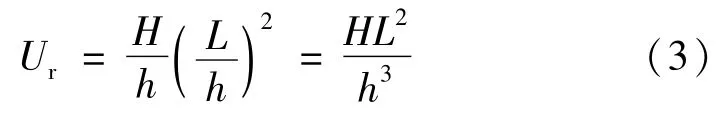
根据式（3）将所有试验组次的Ur算出后与δe的关系如图7所示，得到波浪沿程δe与Ur呈现较明显的负相关关系，且δe随着Ur的增大，变化率逐渐减小。对图7中的数据点拟合得到δe与Ur的幂函数关系式：

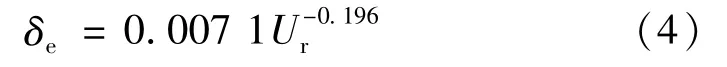
拟合公式的残差平方和为7.28×10-4，拟合结果较好。

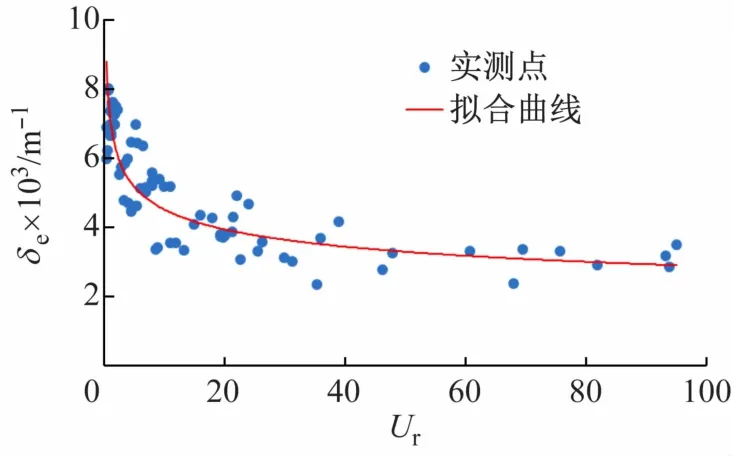
图7 衰减系数与厄塞尔数的关系

2.4 波浪快速率定方法

根据厄塞尔数和衰减系数的关系，计算目标波浪所需的初始造波波高，率定输入的波高计算方法如图8所示。

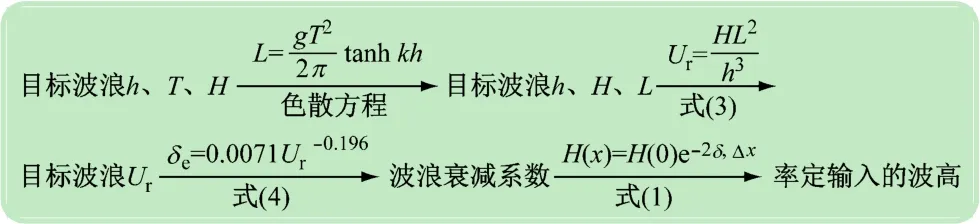
图8 率定波高计算方法

以M501216组次为例，根据图8所示计算过程，依次通过色散方程、式（3）、（4）和（1）得到L＝2.05 m，Ur＝5.38，δe＝0.005 1，目标波浪处（＃18 根波高仪）距造波板25 m，代入式（1）中求得率定输入的波高H（0）＝0.207 m。由此算例可知，虽然衰减系数只有10-3量级，但对波浪长距离传播的波高的影响会通过指数函数放大，所以在波浪实验尤其是Ur较小时的率定需要认真考虑衰减的影响。

M501216组次未考虑衰减H（0）＝0.16 m和考虑衰减H（0）＝0.207 m目标波浪处的稳定的波面过程η-t对比如图9所示，考虑耗散衰减前后的波高分别为0.128 m和0.156 m，考虑耗散衰减的波高更符合目标波浪要求，实际波高与目标波高的误差由20%减少至2.5%，较好地提高了造波精度。

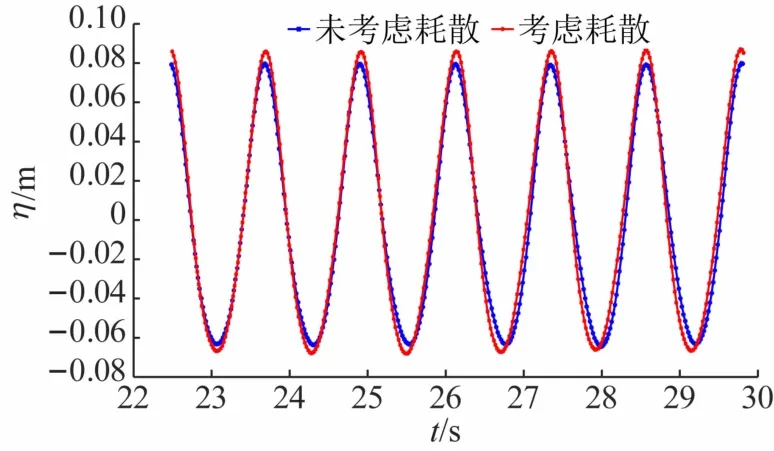
图9 考虑衰减前后指定位置处的目标波浪对比

3 结 语

基于波浪沿程衰减规律以及衰减系数与厄塞尔数的关系，可以通过目标波浪基本要素计算得到控制造波板运动的率定波高，快速地在特定位置模拟得到所需的目标波浪。在水槽中进行波浪实验时，率定波高的准确输入，不仅能够提高造波效率，还能预判目标波浪出现的区域并实现目标波浪的精准测量。通过该实验的学习，学生可掌握波浪测量方法，波浪耗散影响因素，微幅波理论无粘假设的适用范围以及精准快速造波的方法，有利于学生更好地理解和学习波浪理论相关课程并提高波浪试验能力。