砂土剪胀特性的试验研究

卢真辉，戚承志，姜 宽，李太行，崔英洁

（北京建筑大学土木与交通工程学院，北京未来城市设计高精尖创新中心，北京100044）

0 引 言

土具有诸多特性，如硬化或软化特性、压硬性以及剪胀性等。其中，剪胀性是砂土最重要的特性之一。砂土的剪胀性是指土体在活动过程中由于土颗粒之间的排列方式改变引起相互位置的变化，从而使土体产生膨胀或剪缩的特性。为了探究砂土剪胀特性的影响因素及变化趋势，国内外的专家学者对此做了大量的试验研究。Dafalias［1］发现砂土的剪胀性会受砂土的密度和围压的影响；Vaid等［2］发现，初始状态相同的同种砂样在不同应力路径下表现出不同的剪胀性；邵生俊等［3］认为应力路径会引起土体的剪缩剪胀；李广信等［4］、刘元雪等［5］认为砂土的体缩与土的物理性质、试验的应力路径、边界条件等因素有关；罗汀等［6］对黏土和砂土剪胀性的应力路径依存性做了系统的分析和比较；孙汉芳［7］发现在不同的应力路径下砂土表现出不同的剪胀特性；蒋立［8］通过模拟砂土的流滑应力路径三轴试验，探究了流滑应力路径下砂土的剪胀性。

国内外学者虽然研究了多种应力路径对于砂土剪胀性的影响，但是对于建立一种能够反映两者之间关系的本构模型而言，现在的试验数据还远远不够；目前的大多数试验主要集中在简单的应力路径，但这些试验是否能够反映砂土在复杂加载路径中的剪胀规律还鲜有研究。

为了探究应力路径对于砂土剪胀性的具体影响关系，建立能够合理反映砂土应力路径与剪胀性关系的本构模型，更好地描述砂土的剪胀特性，本文在不同固结方式、应力路径、围压下开展了砂土的三轴压缩试验，探究了砂土在不同条件下的剪缩、剪胀变化规律以及剪胀性变化趋势的影响因素。

1 试验土样及方案

1.1 试验仪器功能

本试验采用英国GDS伺服电动机控制的（DYNTTS）动三轴测试系统。通过GDSLAB软件可以准确地完成试验控制和数据采集功能。压力室包括一个内置传感器和量程为2 MPa的围压、孔压传感器。轴向力和轴向位移通过压力室底座的一体化马达驱动螺旋驱动器提供。通过变换内置底座和三轴拉伸顶盖，可制作直径为38、50、70、100、150 mm 的试样。为了操作方便，采用直径为38 mm的底座。压力室内部有可以根据试验要求进行调换的荷重传感器，它可以将比较松软的土质材料变成很硬的土质。因为荷载传感器决定试验系统测试时的最大轴向承载能力，为了满足试验的轴向力的设定，同时也为了能够准确地表示试验时的轴向力，所以本试验选择了量程为2 kN的传感器，压力测量精度0.1%，轴向位移精度0.07%，位移分辨率0.08 μm。围压和反压控制子系统由GDS数字压力/体积（2 MPa/200 cm-3）控制器完成，其分辨率可达1 kPa。

1.2 试验土料

采用筛析法测量级配，砂土试样的颗粒级配分布如表1所示。

表1 砂土颗粒级配

将试验中材料，按《GB/T 50123-1999土工试验方法标准》进行试验。经过测定，得到了土样的基本物理力学指标。其中，密度Gs＝2.66，相对密度Dr＝65%，砂土为中密砂；泊松比ν＝0.33，最大、最小孔隙比分别为：emax＝0.76，emin＝0.47；制样干密度ρd＝1.65 g/cm3。

1.3 试验方案

按照《GB/T 50123-1999土工试验方法标准》的要求制成试验需要的试样尺寸（直径38 mm，高度76 mm）。制样时，不同的装样方法会对试验结果造成影响。采用干装法装样，试样都会表现为应变软化以及剪胀现象；而采用湿装法装样，试样基本上都会体现出应变硬化和剪缩现象［9］。为了考虑应变硬化阶段的变化规律，采用湿装法进行装样。首先称取150 g标准砂，经过煮沸、冷却。装样前，检查仪器各阀门管路是否完好，进行设备调零。所有设备都检查合格后，进行装样。正确安装压力室后进行通水，然后通二氧化碳15 min、水头饱和30 min，该过程试样内的气体被排出；最后通过五级反压饱和，反压饱和过程中有效围压始终保持在20 kPa，该过程由于反压增大，试样内部孔隙水承压增大，饱和度增加，以便使试样的饱和度能够达到实验要求。

通过测量孔隙水压力参数B（B值为Δu/Δσ3＞0.95）检查试样是否充分饱和。当B＞0.95时，即认为土样达到饱和要求，可以进行固结试验，否则需要进一步加压饱和。随后通过GDSLAB软件中的固结模块对试样进行固结；如果超过5 min而试样体积变化小于5 mm3，则认为固结试验完成。固结完成后，按照设定好的Stress Path试验模块进行应力路径三轴试验。图1为试验过程中剪胀破坏前后的试样。

图2是4种应力路径的加载示意图。路径Ⅰ：常规三轴试验，试验时围压保持不变，轴向应力不断增大；路径Ⅱ：等p试验，轴向应力不断增大时，围压减小，而平均主应力保持不变；路径Ⅲ：等σ3试验，轴向应力增大的同时，围压保持不变；路径Ⅳ：等σ1试验，轴向应力保持不变的同时，围压不断减小。路径Ⅰ是等压路径试验；而路径Ⅱ、Ⅲ、Ⅳ路径都是在偏压固结条件下（kc＝2.0）的试验。

图1 试验中的试样

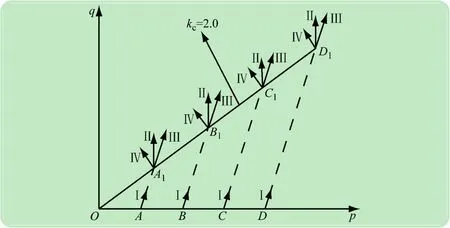
图2 应力路径示意图

2 试验加荷控制方式的影响

GDS多功能三轴仪不仅可以实现应变控制加荷，即按照设定的加载速率进行加荷；也可以实现应力控制加荷，即按照设定的应力路径进行加荷。为了探究剪切方式对砂土力学特性的影响，分别进行了应力、应变控制式下的常规三轴试验，将两组试验结果进行对比分析，讨论控制加载方式的影响。

图3是有效围压100 kPa下常规三轴试验的应力控制式和应变控制式的试验结果对比图，表示的是剪应力q与轴向应变ε1的关系曲线。从图中可以看出，采用应力控制方式时，应力-应变曲线的初始阶段数据点比较密集，后面材料达到屈服状态时数据点较少；而采用应变控制式时恰恰相反，初始阶段数据点比较少，后期数据点显得比较密集。不管是应力控制式，还是应变控制式，这两种加荷方式下的剪应力与轴向应变的关系曲线基本上是处于重合的状态，说明控制加载方式对于砂土的试验结果几乎没有影响。因此，通过这两组试验结果的对比，在一定程度上认为剪切控制方式不会影响本次实验的所有试验结果。

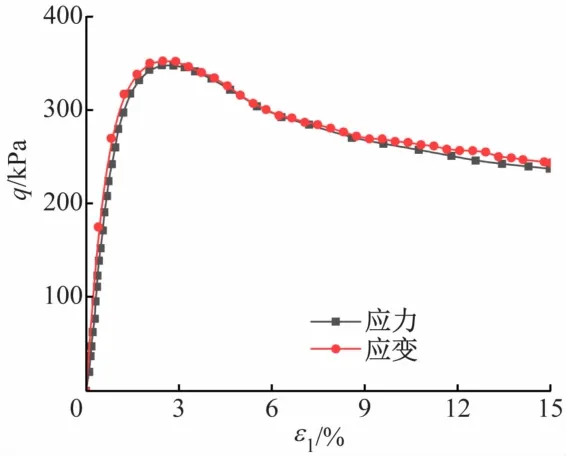
图3 应力、应变控制方式试验结果对比

本试验主要讨论不同固结方式、不同应力路径对砂土试验结果的影响。所有试验都是在固结排水（Consolidated Drained，CD）条件下进行的，试验时采用应力控制式加荷。常规三轴试验，当试样的轴向应变ε1达到15%时，认为试验加载到破坏状态，试验会自动终止；偏压固结试验时，当试样的轴向应变ε1达到5%时，认为试样达到破坏标准，试验终止（见图3）。

3 试验结果分析

3.1 应力路径分析

图4 为等压固结（kc＝1.0）和偏压固结（kc＝2.0）两种固结方式下，从初始状态点（p0，q0）即（0，0）按照原先设定好的固结路径分别到点D（400，0）、D1（533.3，400），然后按照应力路径Ⅰ、Ⅱ、Ⅲ、Ⅳ进行试验的平均主应力p与剪应力q的关系曲线。从图可知，初始状态相同，加载的应力路径不同，每一组试样所表现出的强度特性具有明显的差异性；不同的固结方式，沿着相同的加载路径，得到的强度基本一致。等压固结和偏压固结这两种固结方式，在保持围压σ3＝400 kPa不变的情况下，后期的有效应力路径基本重合，符合试验要求。由图中的有效应力路径可以看出，试验准确地实现了预先设定的应力路径，达到了试验要求。前期固结方式不同，后期加载路径相同，达到的强度值也相同，说明不同的固结方式基本上不影响饱和砂土的强度。

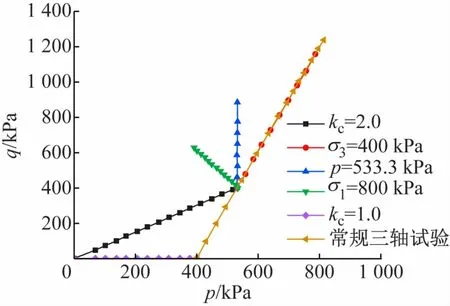
图4 有效应力路径

p-q关系曲线中，砂土试样的平均主应力p和初始剪应力q为：

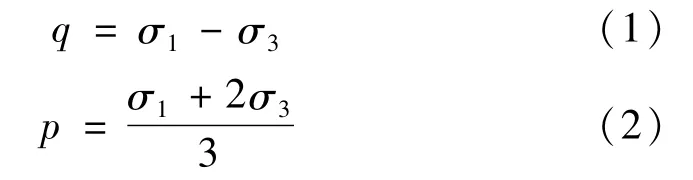
固结过程分为等压、偏压固结，不同的固结方式表示不同：

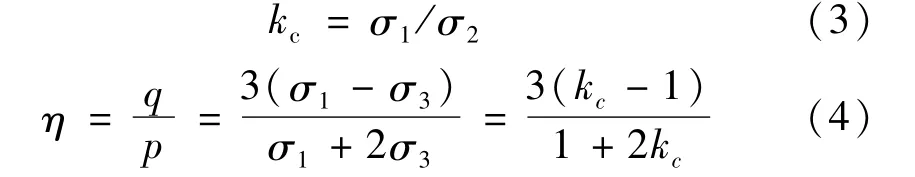
式中：kc为固结应力比；η为应力比。当kc＝1.0时，η＝0；kc＝2.0时，η＝0.75。

实验中不管偏压固结试验，还是等压固结试验，对于等σ3试验阶段来说，路径Ⅰ、Ⅲ加载时都是η＝3.0，即认定为p-q曲线的斜率。但是对于偏压固结下的路径Ⅱ、Ⅳ来说，由于在加载过程中有效围压会不断地发生变化，它们加载时分别对应的应力路径斜率又有所不同，路径Ⅱ：η＝0；路径Ⅳ：η＝-1.5。

3.2 强度分析

图5所示为4种应力路径共计16组试验的峰值强度与平均正应力的关系曲线。从图中可以明显地看出，所有的峰值点基本上是在一条直线上，拟合曲线更是证明了这一点。拟合线表示剪应力与平均主应力是一种线性关系，这符合图2中的应力路径的设定。

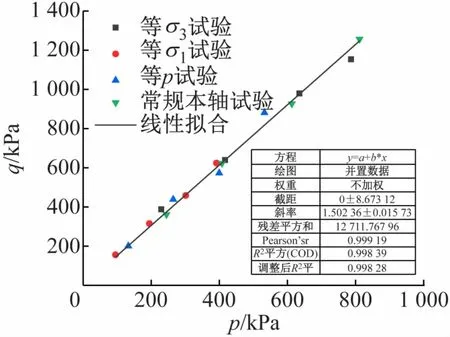
图5 峰值强度与平均正应力关系曲线

临界状态是指土体在整个变形过程中所能达到的一种极限状态，此时不管是土体的体积，还是有效平均正应力、剪应力都不会再改变［10］。砂土还有另外两种状态，相变状态是紧砂或中密砂在不排水过程中出现的状态，是指孔隙水压力由增加到减小的突变状态。而砂土的特征状态是紧砂或中密砂在排水过程中出现的状态，是指土体体积变形由压缩到开始膨胀的突变状态。临界状态土力学一般都被认为是土体本构模型发展的基础，经常用来描述黏性土的应力-应变关系。对于砂土而言，它与黏土不同，在q-p平面内存在一条临界应力比线，其斜率M为临界应力比（见图5）。将这条关系线定义为本文试验材料的临界状态破坏线，即Mf＝1.50。根据临界状态，当在临界状态破坏线以下时，说明该砂土试样比临界状态“紧密”，处于相对紧密状态，剪切时会发生“剪胀”，而且越接近临界状态，其剪胀性就越强；反之，当位于临界状态线以上时，说明砂土比临界状态更加“疏松”，处于一种相对比较疏松的状态。在试验加载过程中，一旦剪应力与平均主应力中的任何一个值达到状态破坏线，则表明试验中的试样将要达到设定的目标值，试验会随之终止。

从图中可以看出，峰值点在平均主应力较小时比较密集一些，离散性比较小，而随着平均主应力的增大，峰值点变得比较稀疏，离散性比较大，说明峰值强度点的离散性随围压的增大而增大。4种应力路径Ⅰ、Ⅱ、Ⅲ、Ⅳ的峰值强度与破坏时的围压的关系曲线是基本一致的，而且所有的加载路径都是处于三轴压缩的状态。说明在三轴压缩的应力状态下试样的峰值强度和破坏围压的关系受应力路径影响较小。

3.3 砂土剪胀性趋势分析

图6所示为一种非常典型的关于砂土类材料的三轴试验的结果对比图［11］。从图中曲线趋势分析可知，砂土开始试验时初始状态不同，则砂土所表现出来的应力-应变关系和剪胀性也不相同。一些学者通过大量的试验研究得出了具有一些规律性的结论：当砂土材料密度比较小时，在试验初始阶段砂土比较容易出现体积收缩现象，试样开始排水，随着试样体积的不断减小，相对密度逐渐增加，呈现出应变硬化的特性，整个过程只有剪缩，根本没有剪胀，体现为图中的曲线3；不同的是，当砂土材料密度比较大时，试样在加载前期容易从剪缩状态慢慢地变为剪胀状态，在CD试验中，剪胀现象主要表现为试样的体积发生膨胀变化，在这个膨胀过程中，试样的密实状态会随着轴向应变的不断增加逐渐变得松软，这就会表现出一定阶段的应变-软化；与此同时，也会出现应力跌落现象。总之，砂土越密实，试验时剪缩过程就会越短，而剪胀过程就会变得越明显，体现为图6中的曲线1和2。而且从曲线1、2的变化趋势可以看出，低应力水平情况下的应变软化、应力跌落现象会比中等应力水平情况下更加显著，表现的比较明显，能够更好地研究砂土的软化现象。

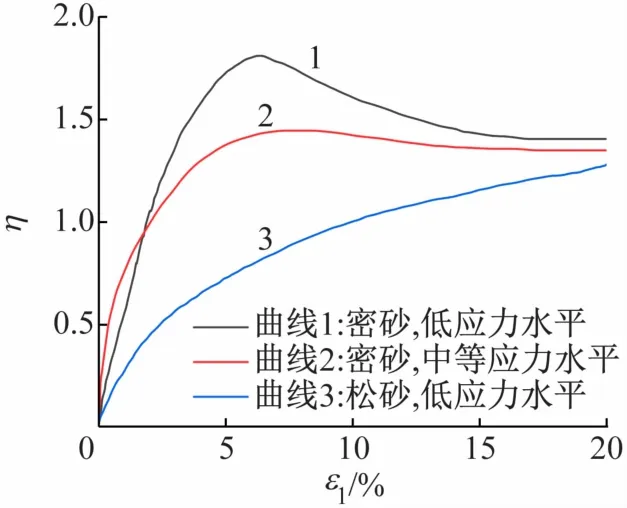
图6 典型的排水三轴剪切试验结果

3.4 围压对砂土剪胀性的影响

图7所示为应力路径Ⅰ～Ⅳ试验的应力比与轴向应变的关系曲线。由图可见，4种应力路径都是从剪缩到剪胀，从应变硬化到应变软化，再到应力跌落的，关系曲线的变化趋势完全符合图6中密砂的特征。这也符合前期测定的该土样的基本物理力学指标中的相对密度Dr＝65%。另外可以看出，路径Ⅰ的关系曲线符合曲线1，表明等压试验试样处于低应力水平；路径Ⅱ、Ⅲ、Ⅳ符合曲线2，说明了这3种应力路径试验的试样处于中等应力水平。

从图7还可以看出，应力路径Ⅱ、Ⅲ、Ⅳ的试验结果都表现出相同的变化趋势，前期偏压固结应力比η＝0.75；而应力路径Ⅰ是等压固结，应力比从初始值η＝0开始。另外，应力路径Ⅰ～Ⅳ试验的峰值应力比都为1.50，这也符合前面得到的临界状态破坏线Mf＝1.50。在同一种应力路径中，当选择不同的有效围压时，虽然整个加载阶段是具有相似性，但是还会存在一定的差异性。在前期的应变硬化试验过程中，在达到相同的应变时，同一种应力路径中不同的有效围压所对应的应力比是不同的，随着围压的增大，对应的应力比在逐渐减小，说明试样的剪缩性随围压的增大而减小。随着轴向应变的不断增大，由应变硬化过渡到应变软化阶段，在应变软化阶段所表现出来的变化趋势与应变硬化阶段恰恰相反，有效围压越大，应力比越大。

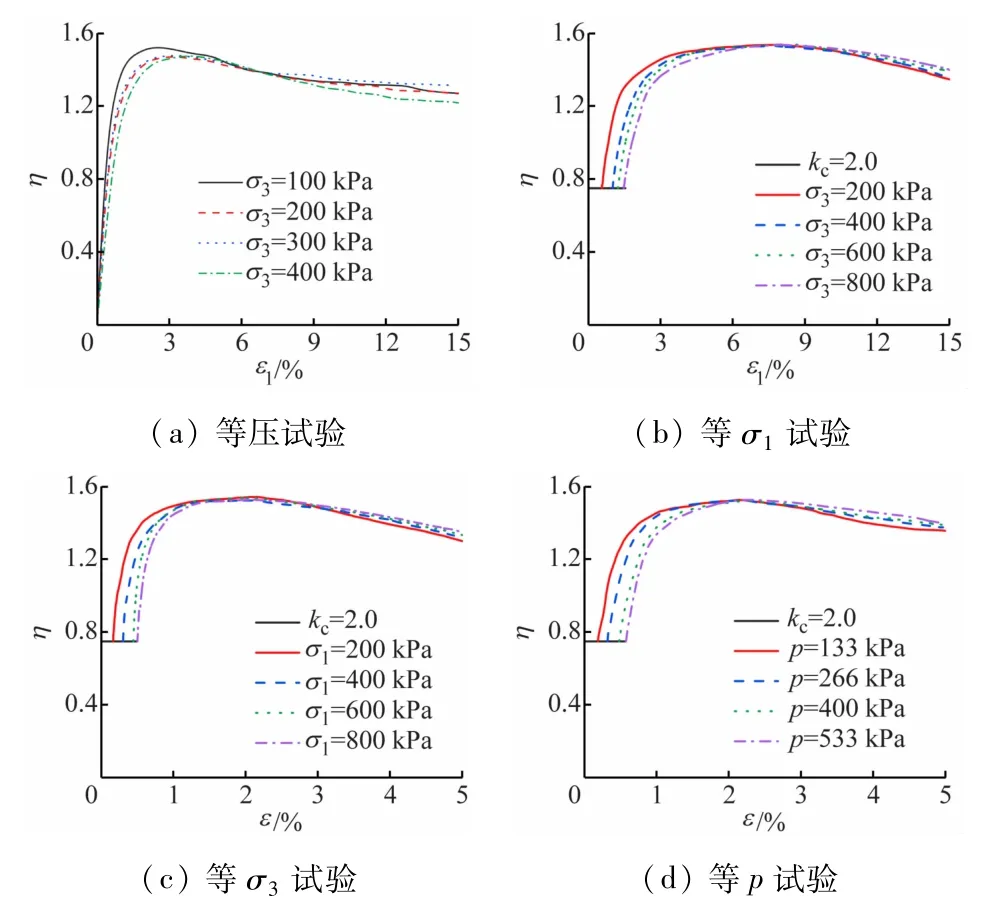
图7 应力比与轴向应变关系曲线

从图7（a）等压试验中可以看出，应力路径Ⅰ在应变软化阶段，不同围压的应力比在减小的过程中会在轴向应变达到6% 时交于一点，说明此时各个试样达到相同的应力状态。从图7（b）、（c）、（d）可以看出，偏压固结下应力路径Ⅱ、Ⅲ、Ⅳ试验的结果则不同，基本上是在轴向应变达到2% ～3%时，就已经交于一点了，相比路径Ⅰ要早一些。不仅如此，等压固结达到相同状态是在应变软化阶段，而偏压固结是在应变硬化阶段，这说明应力路径Ⅰ～Ⅳ试验表现出的剪胀特性在一定的阶段有所不同。

图8所示为在偏压固结条件下，从相同的初始状态点出发的路径Ⅱ、Ⅲ、Ⅳ试验的应力比与轴向应变的关系曲线，由于篇幅限制，在这里只分析C1点。由图可知，CD试验条件下，即使试验的初始状态相同，对于不同的应力路径，试样也是会表现出完全不同的剪缩、剪胀特性。从图中可以看出，初始状态相同，在应变硬化阶段，3种应力路径达到相同的轴向应变ε1时，路径Ⅳ所对应的应力比最大，路径Ⅲ 最小，而路径Ⅱ处在两者中间，说明路径Ⅲ、Ⅱ、Ⅳ的剪缩性是依次增强的；这是因为，路径Ⅲ试验中，平均主应力是逐渐增加的；路径Ⅱ试验中，平均主应力是不变的，而在路径Ⅳ试验中，平均主应力是逐渐减小的，此时起作用的是平均正应力，同时也说明了应力路径对砂土的剪胀性是有影响的。

图8 C1点应力比与轴向应变关系曲线

国内外的专家学者做了大量有关砂土剪胀特性的试验［12-16］，并对试验结果进行了系统的分析。不管是CD试验还是CU（Consolidated Undrained）试验中，试样的剪缩性都会随加载时方向角的增大而逐渐增强。如果定义应力路径加载方向与平均主应力正方向的夹角为应力路径的加载方向角，则路径Ⅲ、Ⅱ、Ⅳ 对应的方向角分别为71.57°、90°、146.31°，角度是逐渐增大的，这就使得上述结论的准确性从另外一个方面也得到了证明，同时本文的试验也对其进行了补充说明，使其更加完善。

3.5 应力路径对剪胀特性的影响分析

图9所示为在偏压固结条件下，初始状态不同时，依次进行路径Ⅱ、Ⅲ、Ⅳ试验的体应变与轴向应变的关系曲线。

图9 Ⅱ、Ⅲ、Ⅳ路径试验体应变与轴向应变关系曲线

根据试验结果，得到了整个加载过程中试样的轴向应变Axial Strain与径向应变Radial Strain的试验数据；然后依据体应变、径向应变、轴向应变三者之间的关系，通过换算得到了加载过程中体应变的变化趋势：

式中：ε3为径向向应变；εv为体应变。

在加载的初始阶段可以明显看出，随着压力的增大，砂土的剪缩性也在变大；这是因为随着加载的进行，初始状态的试样土体颗粒之间的孔隙比随着固结压力的增大而逐渐减小，使得试样的剪缩现象越来越明显，这一复杂现象从砂土的剪胀性机理可以得到合理的解释［17］。密实砂土在开始加载时都会出现剪缩现象，一段时间后出现剪胀现象，砂土的剪缩、剪胀现象会有一个临界点存在，称之为相变点；试样越密实，相变点越靠前，则剪缩过程会越短，而剪胀过程就会变得越来越明显。

由图9可以看出，偏压固结完成后，试样会发生体缩现象以及体胀现象。在后期的剪胀阶段，路径Ⅱ、Ⅲ、Ⅳ试验的体积应变与轴向应变在一定程度上表现为线性关系，而且3种路径的关系曲线基本上是保持平行状态，其斜率大致上是一样的，这也符合试验设定，也说明加载速率保持一致。从图9整个过程中可以看出，在加载的初期阶段，路径Ⅲ、Ⅳ的剪缩性基本上不明显，都体现出较强的剪胀性，而路径Ⅱ表现明显的剪缩性。从图中还可以看出，路径Ⅱ、Ⅲ、Ⅳ在达到相同的轴向应变时，路径Ⅲ、Ⅳ、Ⅱ的体积应变是依次增大的，说明加载后期阶段，Ⅱ、Ⅲ、Ⅳ都表现出强烈的剪胀性，而且路径Ⅲ、Ⅳ、Ⅱ的剪胀性是依次增强的，这与之前通过应力比与轴向应变的关系曲线分析得到的结论：应力路径会影响砂土的剪胀性，基本上是吻合的。

4 等p试验结果及讨论

图10所示为在偏压固结时，以4个不同的初始状态点进行路径Ⅱ试验的体应变、径向应变与轴向应变的关系曲线。由于篇幅限制，本文只对路径Ⅱ的试验情况进行讨论。从图中可以看出，在剪胀阶段，体应变与轴向应变呈现出一定的线性关系。虽然在不同的加载路径下，轴向应变与径向应变的关系曲线不同，但是轴向应变和径向应变也表现出一种线性关系，说明相同的路径下试样的剪胀趋势保持一致即剪胀速率一致。

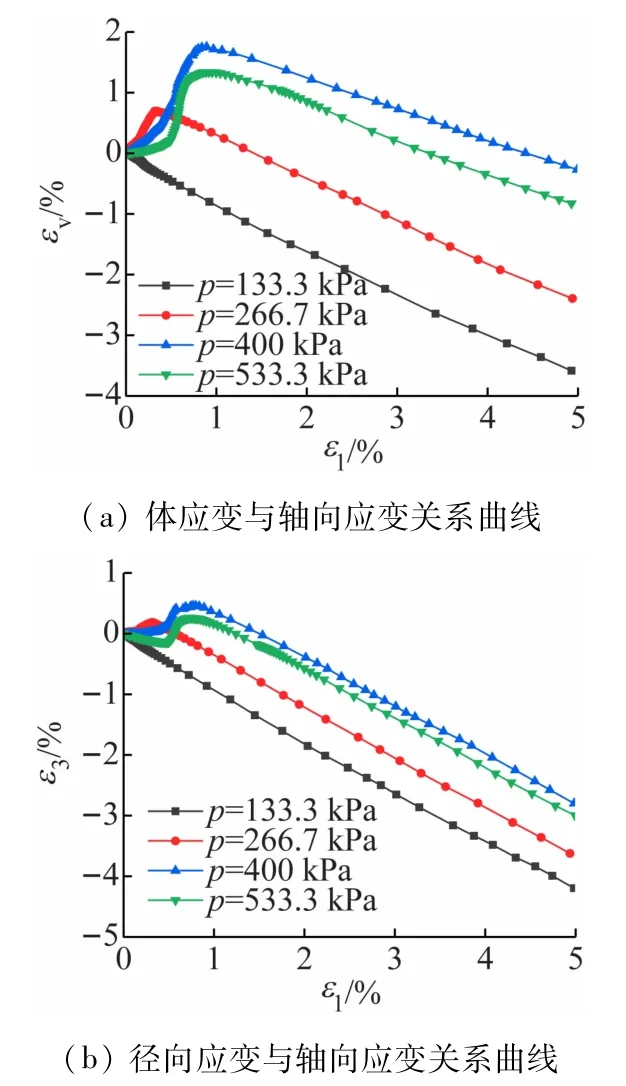
图10 等p试验结果

由图10可以看出，路径Ⅱ的4组试验，虽然固结方式相同，加载路径相似，但是初始加载点不同，得到的试验结果也不一样。在较低围压p＝133.3 kPa时，砂土试样表现出非常明显的剪胀现象；但是随着围压的逐渐增大，可以看出剪胀的趋势在缓慢减弱，向剪缩现象靠近，围压较高时，则先发生剪缩，再发生剪胀。从图中可以看出，每一组试验所达到的最大体应变不同；围压p＝266.6 kPa的试验在应变0.5% 时开始剪胀，而在较高围压p＝400、566.7 kPa试验时应变达到1% 才开始出现剪胀现象，说明不同的等p试验所对应的相变点也不一样。在围压低于p＝400 kPa时，随着围压的增加，试样达到峰值体应变，即相变点时，所对应的轴向应变也在增加，同时剪胀性越大。另外可以看出围压越小，越快出现剪胀；围压越大，前期剪缩现象越明显。但是当围压达到p＝533.3 kPa时，可以明显看出，体应变相对于p＝400 kPa反而减小了，即剪缩性减弱了，这说明在两者之间一定存在一个转变的围压值。通过对等p试验的结果分析可以知道，不同围压下的剪胀性是不同的，而且高围压下试样的剪胀性与低围压也不一样，说明围压对砂土的剪胀性有影响。

5 结 论

由上面的分析可以得到以下结论：

（1）在相同的有效围压下，两种不同固结方式试验的试样强度保持一致，说明固结方式基本上不影响饱和砂土的强度。应力路径Ⅰ～Ⅳ的峰值强度与破坏围压的关系曲线基本上是一致的，而且所有的加载路径都处于三轴压缩状态，说明在三轴压缩的应力状态下峰值强度和破坏围压的关系受应力路径影响较小。

（2）根据不同的应力路径进行试验加载，试样会表现出完全不同的剪缩、剪胀特性。等压固结的常规三轴试验和偏压固结的等σ3试验、等p试验、等σ1试验，在应变硬化阶段的剪缩性是随着围压的增大而减小的，而在应变软化阶段的剪胀性是随围压的增大而减小的，说明围压会影响砂土的剪胀性。偏压固结条件下初始状态相同时，3种应力路径等σ3试验、等p试验、等σ1试验的剪胀性是依次增强的，说明应力路径会对砂土的剪胀性造成影响。

（3）偏压固结条件下，在等p试验的剪胀阶段，试样的体应变、径向应变随着剪应力的增大而与轴向应变呈现一种线性关系；相同的路径下，试样的剪胀趋势保持一致即剪胀速率一样。围压低于p＝400kPa时，围压越大，剪缩现象越明显；围压越小，剪缩现象越不明显，越快出现剪胀。随着围压的逐渐增加，试样达到相变点时所对应的轴向应变也在增加，剪胀性越大。当围压达到p＝533.3kPa时，其所对应的体应变相对于p＝400kPa时反而减小了，剪缩性减弱了，这说明在两者之间一定存在一个转变的围压值，也说明高围压下的剪胀性与低围压剪胀性有所不同。