大功率并网逆变器多采样控制研究
江宏玲,周 成
(1.安徽省·水利部淮河水利委员会水利科学研究院,合肥230088;2.安徽省建筑工程质量监督检测站,合肥230088;3.安徽国际商务职业学院,信息工程学院,合肥231131)
0 引 言
随着新能源市场的蓬勃发展,大功率光伏逆变器的应用越来越广泛,而电压和电流等级的不断增大使得大功率逆变器在控制上有诸如:考虑降低损耗而不得不使用较低开关频率、LCL谐振峰过大等难点。因此,其控制策略上的探究热点包括:如何在控制时采用尽可能低的开关频率,如何对LCL滤波器的固有谐振峰进行抑制、采取何种采样(单采样、双采样、多采样)方法进行控制。一般大功率逆变器采用低开关频率控制时所普遍采用的脉宽调制(Pulse Width Modulation,PWM)控制通常为单/双采样调制模式,低开关频率导致引入的控制延时对系统的控制性能有较大危害,电流谐波抑制和动稳态性能等方面效果较差。如何减小计算延时和PWM延时是完成低开关频率下控制的关键,而文献[1-2]中所提出的研究方法,如:虚拟电阻法、陷波器法、基于状态反馈法等均无法减小PWM控制延时。对于大功率逆变器所普遍使用的LCL结构存在的较大谐振峰问题,目前的解决方案有有源、无源、无阻尼控制等方法。改进控制算法实现阻尼的增加的有源阻尼控制能够抑制谐振峰,但文献[3]中虚拟电阻法无法减小PWM控制延时,文献[4]中陷波器法由于磁饱和影响LCL滤波器参数致使控制效果较差,文献[5-6]中基于状态反馈法由于需要额外的传感器使得系统成本增加。相对于有源阻尼控制的无源阻尼法[7-8],虽然算法简单有效但存在系统损耗较大、衰减高频谐波能力差等缺点。其实,解决上述问题的关键是如何在低开关频率控制下有效减小计算延时和PWM控制延时,通过使用多采样控制策略能够解决。
1 并网逆变器的多采样有源阻尼控制
传统的逆变器控制策略中所普遍采用的是单、双PWM调制采样模式,这种采样模式使得系统在控制时的计算延时和PWM控制延时较大,导致系统的电流谐波抑制和动稳态性能等方面效果较差。将多采样PWM调制方法应用于有源阻尼控制策略中,能够维持在较低的开关频率同时减小计算延时和PWM控制延时,从而对谐振峰进行抑制提高控制性能。
1.1 多采样PWM调制原理
在传统采样PWM调制模式下,调制波装载采样值的时刻是在三角载波的波峰或波谷处,其中,单采样是在波谷或者波峰处装载而双采样是在波峰和波谷处装载。在进行采样PWM调制时,一般都采用在当前采样时刻采样计算而在下一个采样时刻装载的滞后一拍控制,这样使得无论采用何种采样模式都存在计算延时。但是,在一个开关周期内采样次数越多会使采样计算延时越小,所以采样计算延时可以表示为
Ts/N
式中:Ts为开关周期;N为采样次数,N越大则计算延时越小。图1所示为多采样PWM调制原理,其中采样频率fc与开关频率fs满足fc=Nfs,多采样引入的计算延时Ts/N(其中,N>2)较单/双采样减小,若将多采样PWM视为纯延时环节,则PWM控制延时为Ts/(2N)。采样总延时:
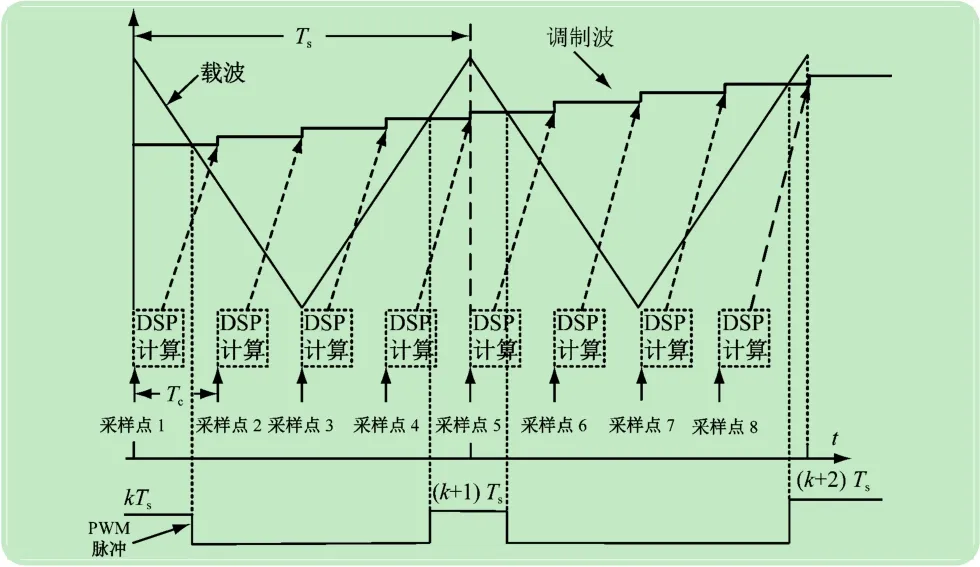
图1 多采样PWM调制原理图
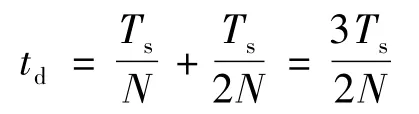
td和Ts成正比[9],较低的开关频率fs会使总延时td增大危害系统性能,维持fs不变增大N,可减小总延时td。对不同的采样次数N的Matlab仿真延时如图2所示,实线为仿真结果与虚线计算值基本吻合。
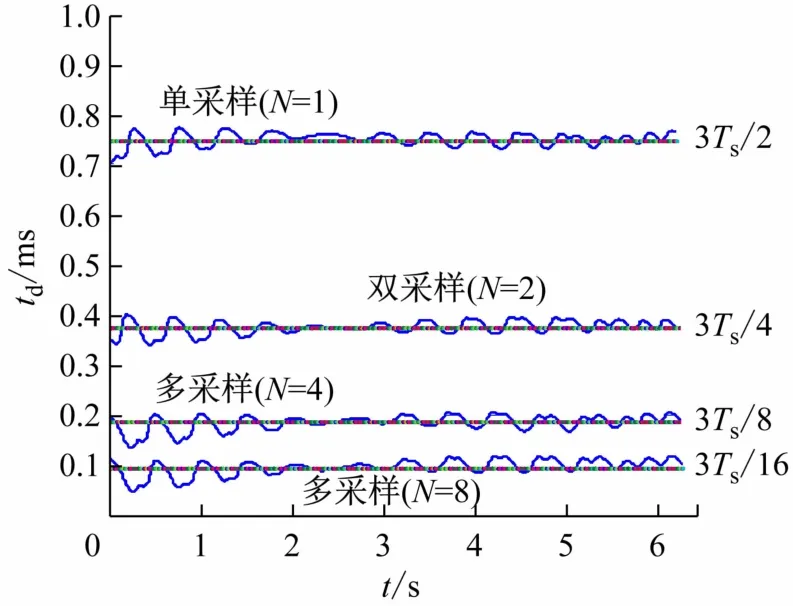
图2 不同PWM采样下的总延时td
1.2 大功率并网逆变器的有源阻尼控制
在大功率逆变器中,由于控制时要求采用较低的开关频率,产生的较大的谐振会影响了系统整体性能。为解决这个问题,常用的方法有有源、无源阻尼法,无源阻尼法虽然简单易行但增加的实际阻尼会大大增加损耗。有源阻尼法有效解决了无源阻尼法的不足,即对谐振峰进行了有效抑制又提高了控制性能。很多文献对其进行过研究[10-11],其中文献[12]中所探究的方案应用较为广泛,如图3所示。本文采用这种有源阻尼控制方式进行算法仿真和实验研究。
图3(a)中,ea、eb、ec分别为电网三相电源,C为滤波电容器,L1、L2为逆变器侧和网侧滤波电感器,ia、ib、ic为逆变器测电流,UDC为直流侧电压。uca、ucb、ucc为电容器C上采样的电压,经过图3所示的[12]环节,式中:k、s、ωfres、Gf()s分别为比例系数、微分算子、谐振频率以及低通滤波器,将有源阻尼环节Q(S)叠加到电流PI调节器的输出。图3(b)中,GR(s)和Gt(s)分别为PI控制器和控制延时。其中GR(s) 和Q(s)[13]为:
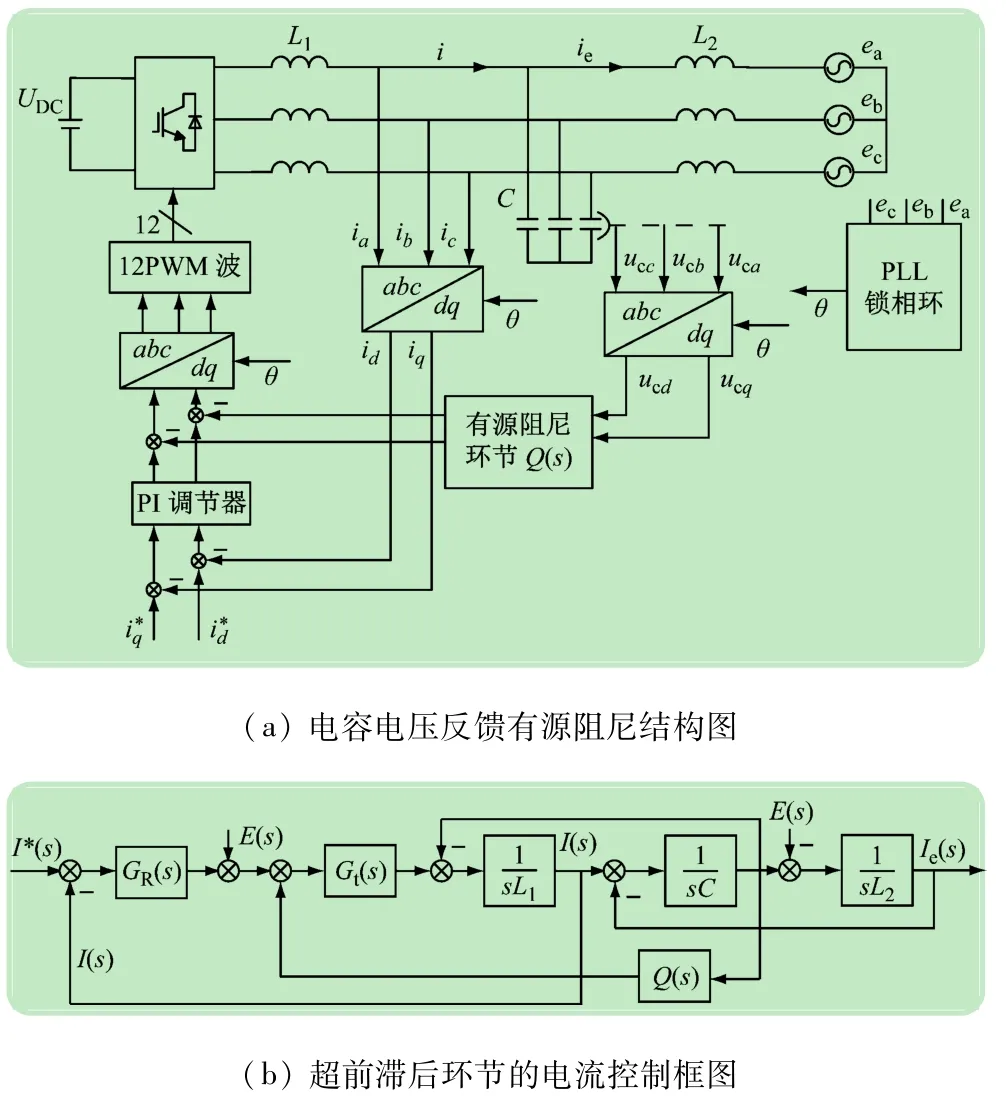
图3 有源阻尼控制结构和电流控制框图
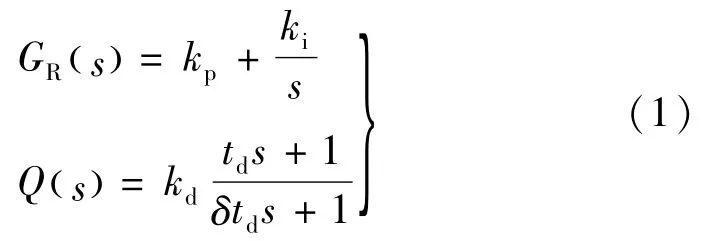
式中:kp为比例系数;ki为积分系数;kd为增益系数;td为时间系数;δ为分度系数。不考虑控制延迟,若采用图3(a)并配置有源阻尼Q(s)为超前滞后环节对抑制谐振峰有较好的效果[13]。但实际上对于大功率逆变器来说,图3(b)所示的延时环节Gt()s不可忽略。而若采用传统的单/双采样,引入的计算延时和控制延时对系统的性能有较大损害,而通过将多采样技术应用于图3所示的控制方案,由于一个开关周期内进行更多次数的采样从而在一个开关周期内达到了减小计算延时和控制延时的效果,实现了系统性能的提高。
1.3 多采样PWM调制存在的问题及解决方法
将多采样PWM调制用于有源阻尼控制策略中,通过增大并选择合适的采样次数N,可以减小系统总延时td从而提高系统控制性能。但与传统的单/双采样相比,多采样PWM调制技术在实现过程中主要存在的两个问题需要解决,一个是调制波与三角载波多次相交造成的多次比较引起的竞争冒险问题;一个是调制波与三角载波可能出现的垂直相交所引起的PWM脉冲丢失问题。本文通过对算法进行改进有效解决了这些问题。
(1)PWM调制波与三角载波多次相交。图4所示为多采样PWM调制条件下PWM调制波与三角载波的多次比较示意图。由图4可见,三角载波在上升段和下降段均与PWM调制波出现多次相交的问题,这样会导致三角载波与PWM调制波出现多次比较的问题。以三角载波下降段为例(三角载波上升段同理),PWM调制波幅值为P3时与载波相交于t4时刻,而在t5时刻调制信号装载更新为P4,又与三角载波相交于t6,产生的多次比较问题会引起的竞争冒险。竞争冒险可能会产生的窄脉冲会引起开关频率变化或系统开关器件误动作、产生额外谐波等危害[14]。本文在算法设计时,采用文献[14]中所述配置方法对DSP的EPWM模块进行相应配置来消除窄脉冲。
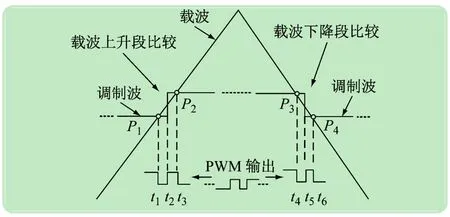
图4 多采样PWM多次比较现象
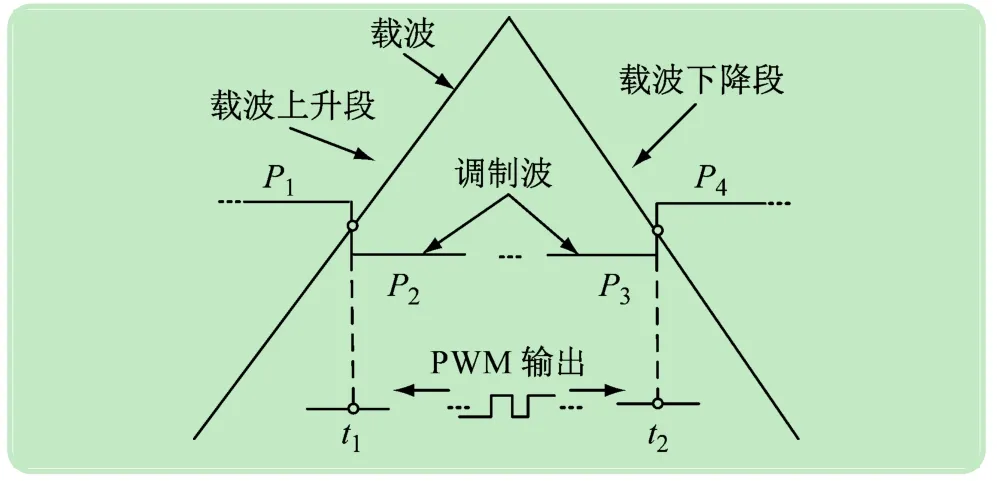
图5 调制波与三角载波垂直相交

图6 PWM调制信号延时输出
(2)PWM脉冲丢失。多采样时,在一个三角载波周期内的上升或下降段都有可能因为多次装载导致如图5所示的三角载波与PWM调制波垂直相交问题。在工程实现时,调制波的装载时刻一般为中断时刻而中断触发到信号写入寄存器之间的延时ΔT会使得在垂直相交发生时造成脉冲丢失。以图6中的三角载波的上升段为例(下降段同理),t1时刻调制波装载,在中断触发的t1时刻若不考虑延时则调制波装载后,幅值由P1变为P2,t1时刻是对应时间基准计数器值TC1,此时计数器值TC1<P2。若不考虑延时,当时间基准计数器值TC1递增到P2时t2时刻电平会翻转,但实际上进入中断后才会进行调制信号更新(ΔT1延时的存在),实际上在t3时刻才会输出P2,此时的计数器值为P1>TC2>P2无法满足计数器的值(TC)等于比较器中的值(CMP)[14]从而造成脉冲丢失。
为了解决多采样条件下出现的垂直相交问题,本文通在算法设计时,叠加一个ΔT延时补偿量到计数器后得到新的TC后再进行比较,有效避免了延时输出造成脉冲丢失。以载波的上升段为例(下降段同理),当TC>P1,则使PWM输出持续低电平,当TC<P1,则将P1正常写入比较器。
2 仿真与实验验证
2.1 仿真结果与分析
为验证上述分析,使用Matlab进行仿真分析,系统仿真的参数设为直流侧电压是220 V,网测线电压110 V,开关频率选择2 kHz,逆变器侧和网侧电感分别为2.2 mH 和1.1 mH,滤波电容60 μF,额定功率5 kW。图7所示仿真结果为在将如图3(b)所示的超前滞后环节Q(S)中kd取不同值的情况下,对双采样(N=2)和多采样(N=4)进行的仿真。
图7中的ic、iec分别为逆变器侧和网侧C相电流,可知kd的选择是否合适,将决定电流波形是否发生失真。超前滞后环节的PI调节器中kp的增大会导致电流波形失真和THD的增大从而影响系统的稳定裕度[15]。图8所示是将如图3(b)中的PI调节器在kp=110情况下对双采样(N=2)和多采样(N=4)进行的仿真。
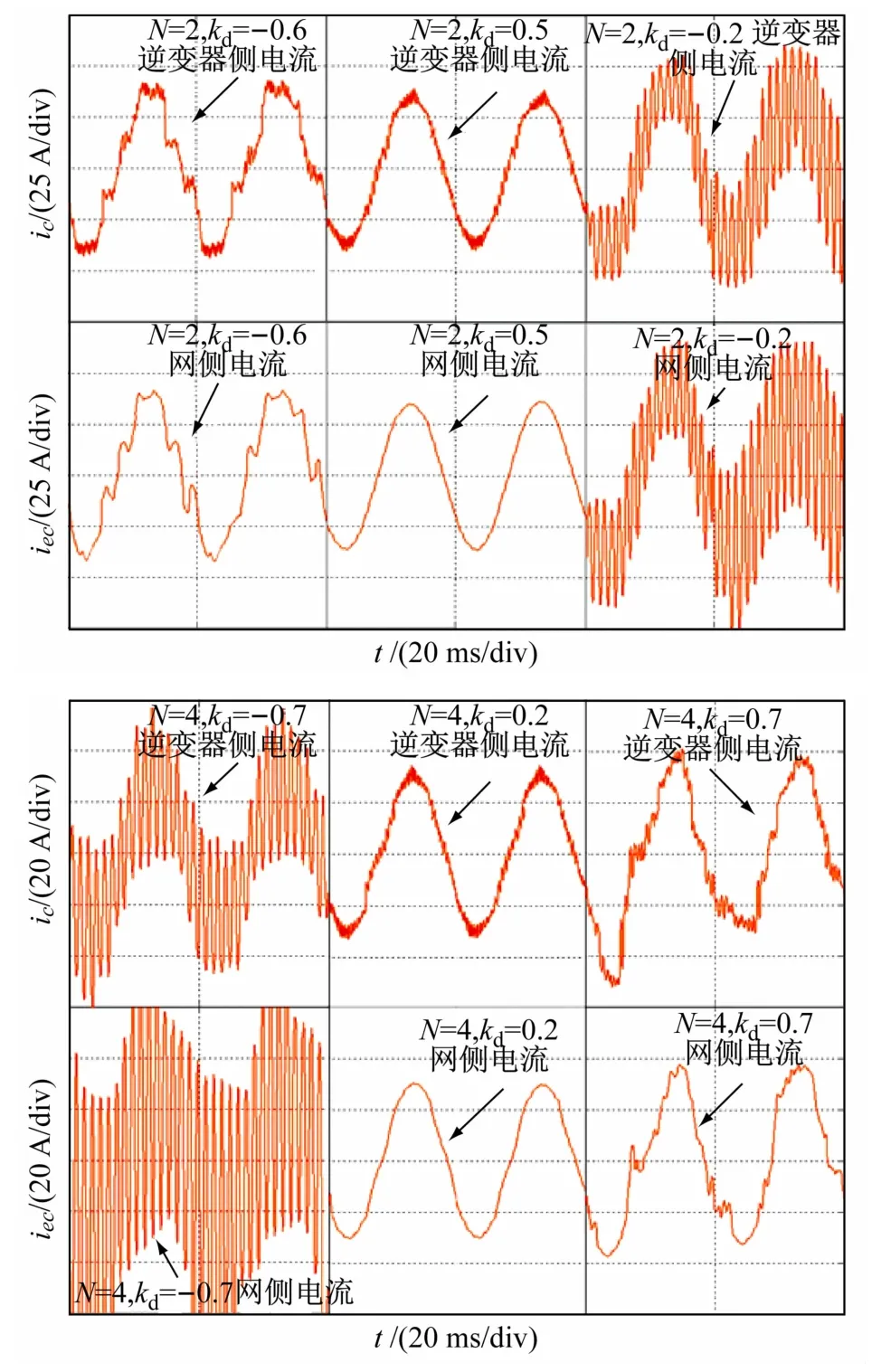
图7 kd值对双/多采样电流波形的影响
图8中的ic、iec分别为逆变器侧和网侧C相电流,可知由于多采样对计算延时和控制延时的减小导致系统在较大的kp下仍能保持良好的电流波形和减小低次谐波幅值和总谐波失真。
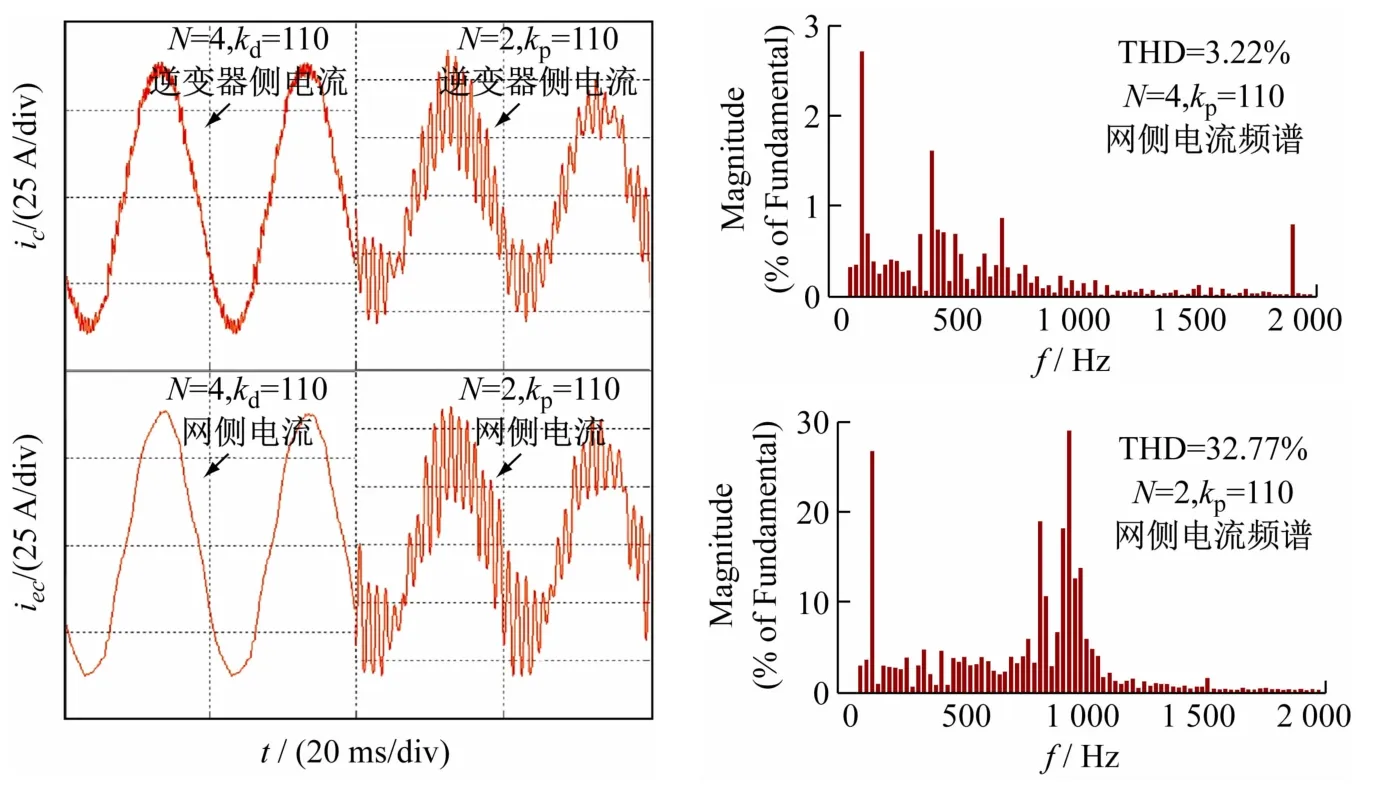
图8 双/多采样电流波形和频谱(kp=110)
2.2 实验结果与分析
在对上述的多采样控制方案进行仿真分析的基础上,构建了DSP+FPGA双芯片实验平台,用于实验验证。实验平台如图9所示。
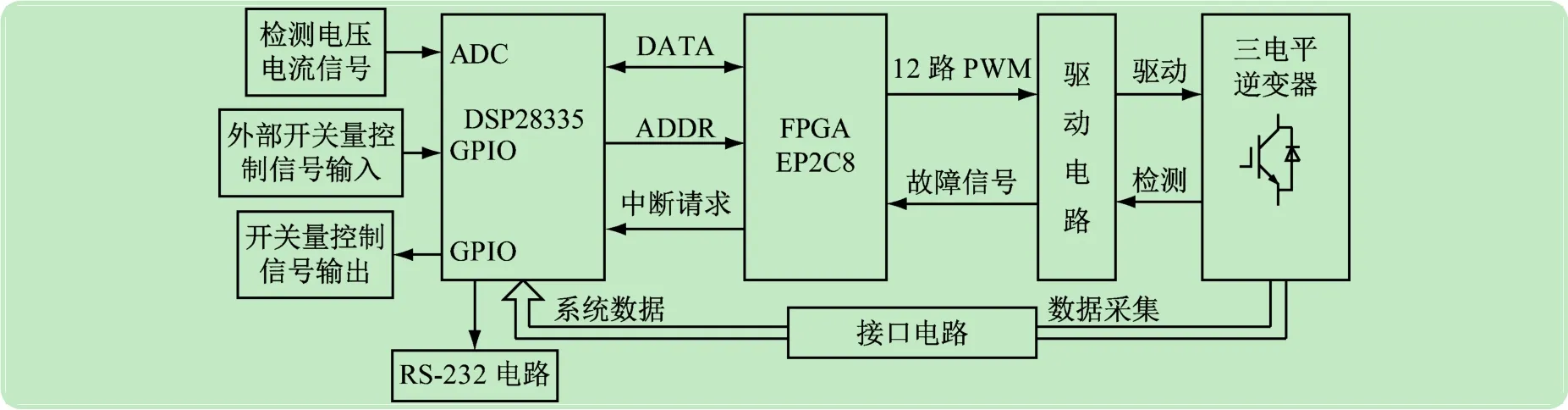
图9 系统控制框图
其中FPGA完成与DSP的数据交换并输出驱动控制信号控制逆变桥,DSP完成信号采集和多采样无阻尼控制以及并网控制功能。图10为基于多采样技术的超前滞后环节的电容电压反馈的实验波形。
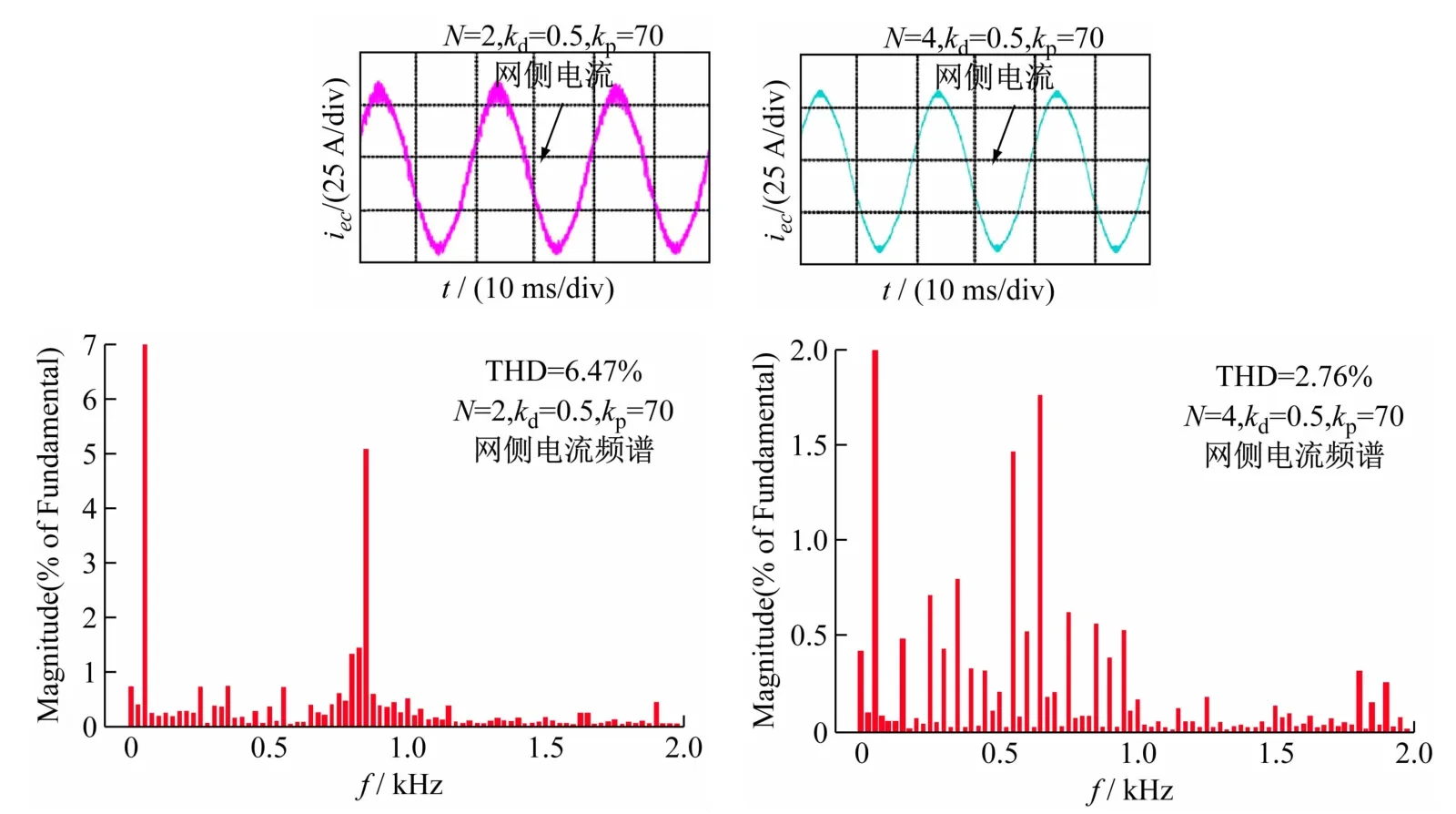
图10 双/多采样网侧电流波形和频谱
为了使双/多采样都能得到较好的网侧电流波形,取kd=0.5、kp=70进行实验。由图10的实波形可知,双采样(N=2)和多采样(N=4)的实验结果对比,多采样的网侧电流iec波形更好且总THD为2.76% <5%,满足并网条件。实验结果表明,采用改进算法解决了多采样的两个主要问题后,可以有效降低计算延迟和控制延迟,提高系统控制性能。
3 结 语
传统采样在NPC三电平大功率逆变器控制时不可避免的引入了计算延时和控制延时,导致系统控制性能不佳。通过在有源阻尼控制中加入改进后的多采样PWM控制技术,在维持较低的开关频率的前提下能够有效减小计算延时和控制延时从而解决低开关频率和采样频率的矛盾并对LCL谐振峰抑制有较好的效果,提高了系统的稳定裕度和控制性能,实现了有源阻尼的高性能控制。

