3层材料层合梁纯弯曲实验测试与分析
蒋 泉,任良琨,丁华建
(南通大学交通与土木工程学院,江苏南通226019)
0 引 言
梁在结构中起承载作用。为了实现特定功能,将几种的材料组合在一起承受结构荷载,称之为层合梁。层合梁具有许多优点,如较高的比刚度和比强度,在土建、机械和航空航天领域具有广泛的应用。於红梅[1]通过测量指定截面上的弯曲正应力,将实验值与理论值对比,分析得出夹层梁纯弯曲时基本满足平面假设条件。唐晓雯等[2-3]对双层金属层合梁弯曲正应力进行了实验测试和分析,验证了双金属层合梁的理论推导正确性,其研究成果可用于材料力学的课程教学及工程实践。马功勋[4]在层合梁应力研究中得到了规则非对称正交层合梁的应力具有非对称的特性。卢玉林等[5]通过实验与数值模拟研究给出了弯曲梁正应力的弹性力学解。杨创战等[6]利用ANSYS的数值计算给出了纯弯曲梁的正应力分布,得出的结果与理论值、电测值基本一致。赵人达等[7]基于ANSYS建立的模型,分析了叠合梁的极限承载力。张士保等[8]通过实验分析了叠合梁的受力性能,给出了拟合公式,可作为工程应用的参考。李杰[9]对双层叠合面组合梁进行了研究,给出界面应变沿梁长的分布规律。刘寒冰等[10]推导出了竖向集中力作用下组合梁的各部分应变,与实验对比误差较小,理论公式正确可行。Keer等[11]研究了半无限层的混合边值问题,可进一步推广至层合梁的分析和研究。Han等[12]基于一阶剪切变形梁理论,给出的层合梁解析解与有限元结果吻合。Hu[13]应用三维应力应变变换关系,建立了T型截面叠层组合梁的总刚度矩阵。Soldatos等[14]提出了适用于任意边界条件下层合梁的精确应力分析方法,通过数值计算,验证了其解析解的正确性。以上工作对层合梁理论和实验等方面的研究提供了参考。
根据现有单、双层层合梁理论和实验分析,基于平面假设给出了3层材料组成的层合梁的弯曲正应力理论公式,并通过层合梁的弯曲实验进行验证,可作为教学实验和实际工程应用的参考。
1 层合梁基本方程
如图1所示,假定3层层合梁的宽度为b;上层、中层和下层材料弹性模量和厚度分别为E1、h1,E2、h2和E3、h3,层合梁总高度h=h1+h2+h3。且x轴位于中性层,与轴线方向一致,y轴为横截面纵向对称轴,z轴为横截面中性轴,距离横截面横向对称轴y0,梁横截面上承受z方向弯矩M。假设层合梁的中性轴位置计算、纵向线应变计算、应力公式推导同样适用。与单层梁类似,在横截面上距离中性轴为y处的纵向线应变为
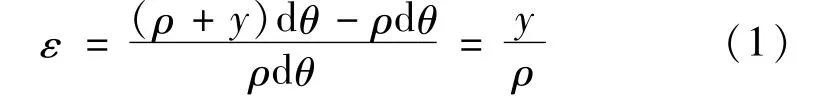
式中:ε为线应变;ρ为中性层曲率半径;y为研究点到中性轴距离;dθ为所研究微段对应圆心角。
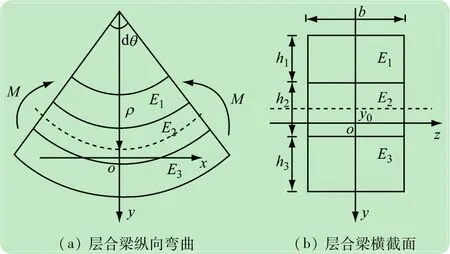
图1 层合梁弯曲示意图
根据胡克定律,在距离中性轴y处的正应力可以表示为

式中:σ为正应力;Ei为各层材料的弹性模量。
对于纯弯曲问题,横截面上轴力FN=0,有如下关系:
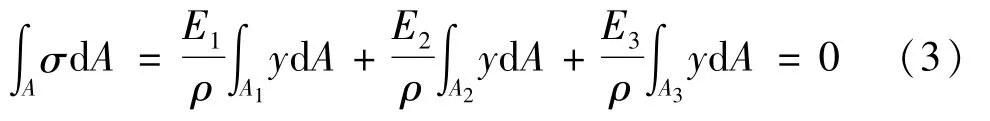
式中:A1、A2、A3和A为各层横截面面积和总面积,进一步整理得到:
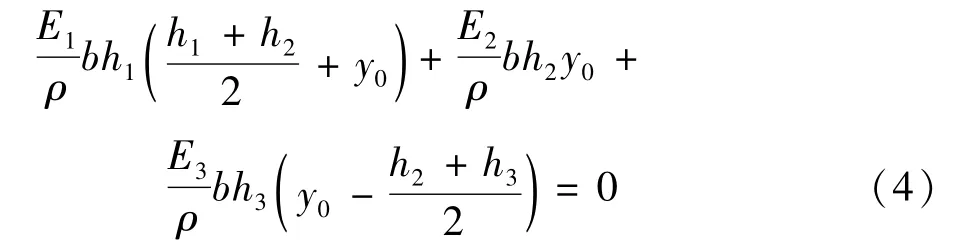
当h1=h2=h3=h/3时,可以得到中性轴y0的位置:
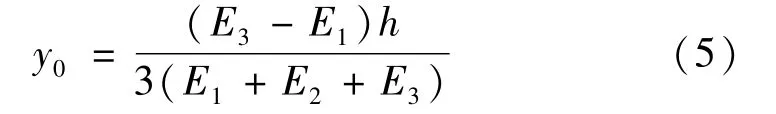
弯矩My的平衡条件为
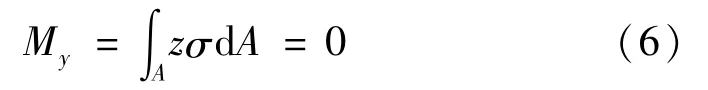
根据对称条件,该静力学自然满足。横截面上的弯矩Mz的静力学条件满足如下关系:
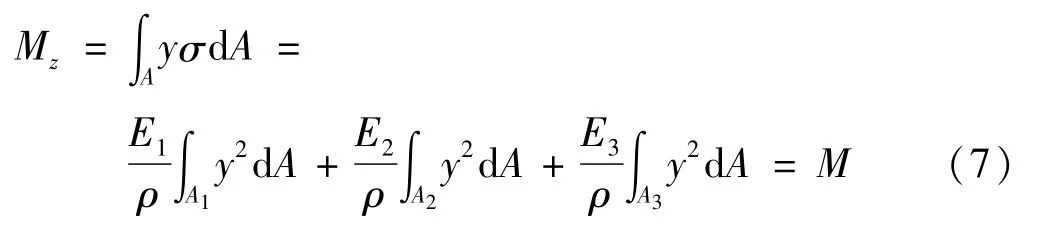
则中性层的曲率为
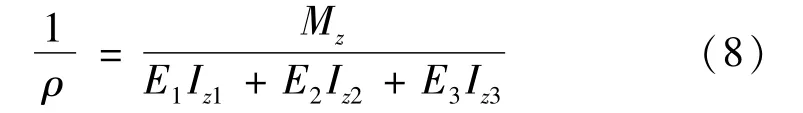
式中:Iz1、Iz2和Iz3分别为各层截面对中性轴的惯性矩。根据式(4)和移轴公式可得到各层惯性矩的具体表达式。将式(8)代入(2)可得各层正应力分布:
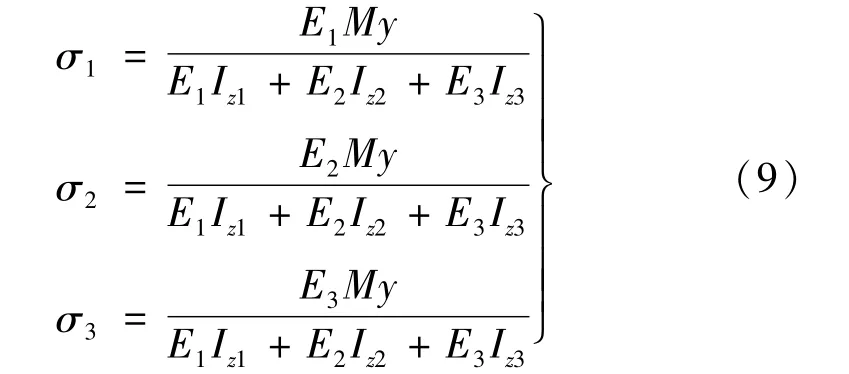
式中:σ1、σ2和σ3分别对应层合梁上、中和下层的应力分布。
2 层合梁弯曲实验测试与分析
实验所用仪器设备为DH3818-1静态应变测试仪、CLDT-C型材料力学多功能实验台(见图2)。共使用了2组层合梁进行应力测试,每组中的3层材料几何尺寸、形状相同,皆为矩形截面梁,尺寸均为b×h=20 mm×14 mm。

图2 层合梁弯曲实验装置
第1组实验对象为由上下两层铜合金和中间一层低碳钢组成的3层层合梁,E1=89 GPa,E2=201 GPa,E3=89 GPa。第2组实验对象为由铜合金、低碳钢、铝合金3种材料组合,E1=110 GPa,E2=230 GPa,E3=75 GPa。将已选择打磨光滑的层合梁使用丙酮擦净,待表面干洁,在每层梁上确定应变片位置并记录具体距离数值,共使用11个应变片,最上层与最下层使用4个应变片,中间层使用3个应变片,每层内的每个应变片之间垂直方向距离为3.5 mm,具体如图3所示。
在实验中,采用0.3 kN的分级加载,一直加载至最大荷载值3.0 kN,记录完数据后卸掉荷载,再进行2次实验,取3次应变测量值的平均值(精确到0.5个微应变)进行分析,具体实验结果如表1和表2所示。
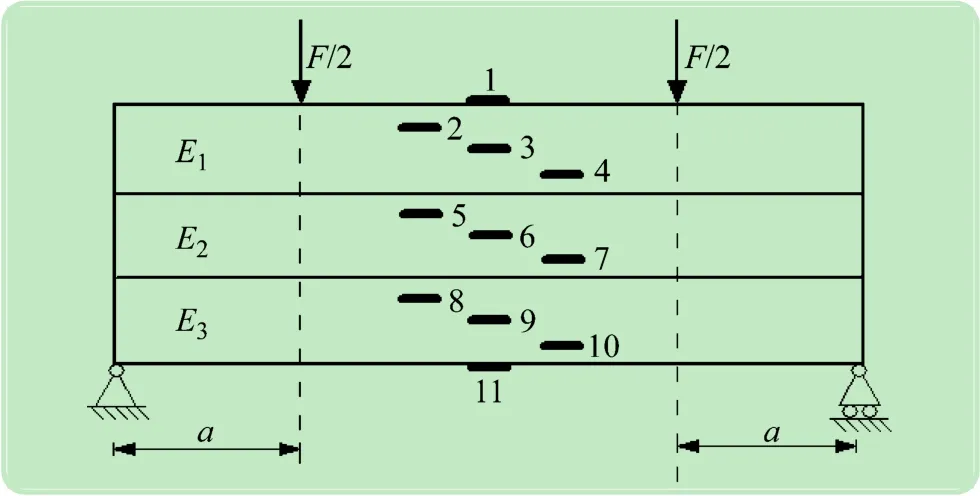
图3 层合梁加载和应变片粘贴情况
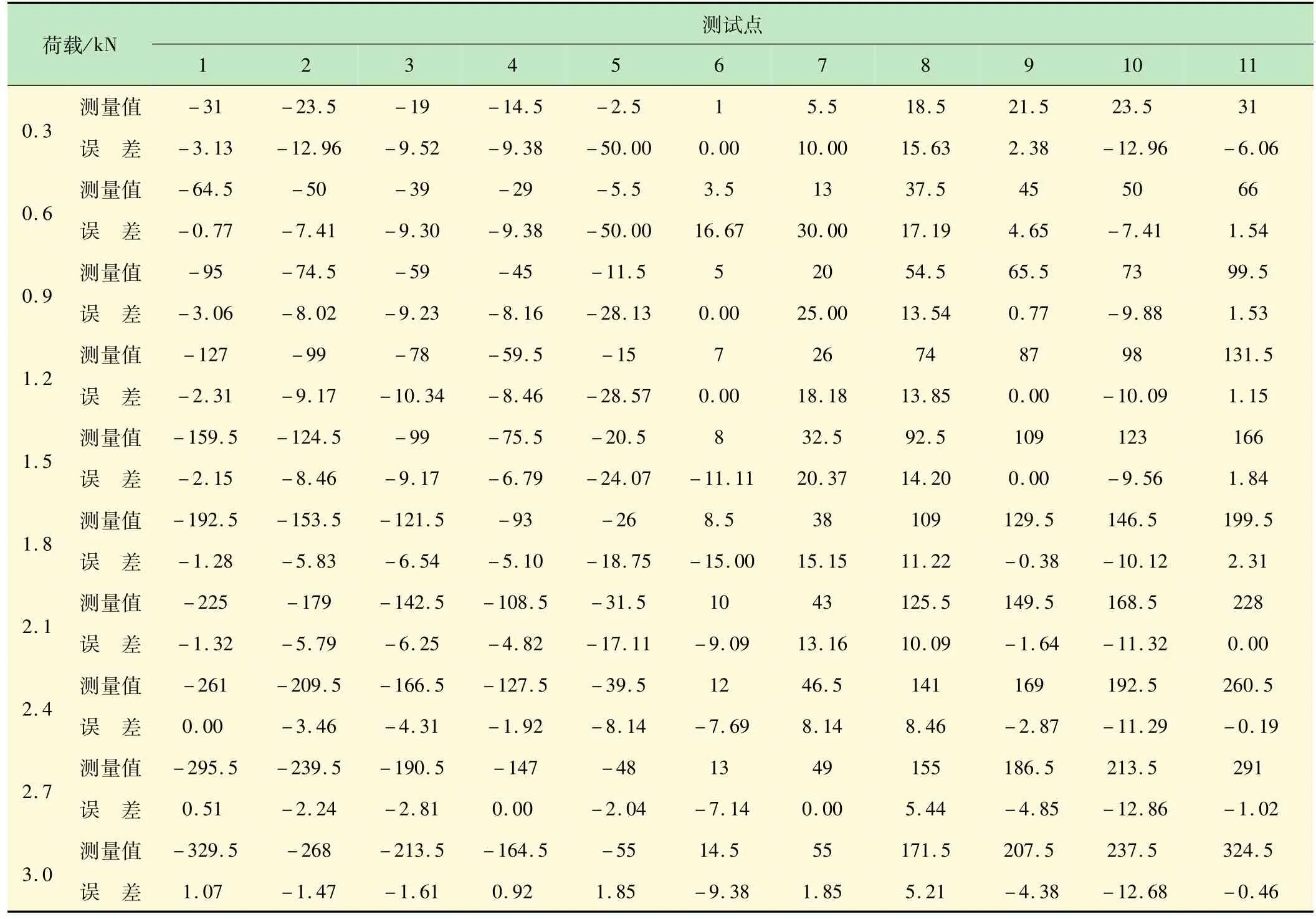
表1 第1组层合梁应变测量值(10-6)与测量误差 %
在第1组实验中,根据式(4)和(5)得到,中心轴位置y0=0,此时6号应变片位于层合梁的中性轴上,理论上应变片测量值为零。考虑到实际粘贴应变片时会有轻微偏离则会导致误差,因而在实验完成后精确测量了第6号应变片的位置及实际距离,并对理论值进行修正,得到表1中修正后的数据后进行误差分析。
此组实验实验值经初步分析符合线性分布,且同级荷载下,1~11号应变片数据呈线性增长与理论计算值一致。本组实验误差基本都在20%以内,大多为10%以内,误差较小,最大误差为50%,最小误差为0%,误差较大情况皆出现在5号应变片,初步分析是第1层材料与中间层材料间的胶水存在一定厚度,5号应变片距离中性轴较近,较小的位置偏差将会引起较大的测量误差。
对于第2组实验,同样根据式(4)、(5)得到中心轴位置y0=-1.69 mm。如表2所示,此组实验测量值随载荷增加均呈线性增长,除7号应变片之外,实验误差基本在20%以内,与理论值符合较好。较大的误差出现在7号应变片,与第1组实验分析一致,其距离中性轴最近,很小的位置误差会引起很大测量误差。6~11号应变片的实验值比理论值稍大,初步分析原因为层合梁在胶合粘结时胶水涂抹较厚,对整个梁的截面高度产生一定的影响。
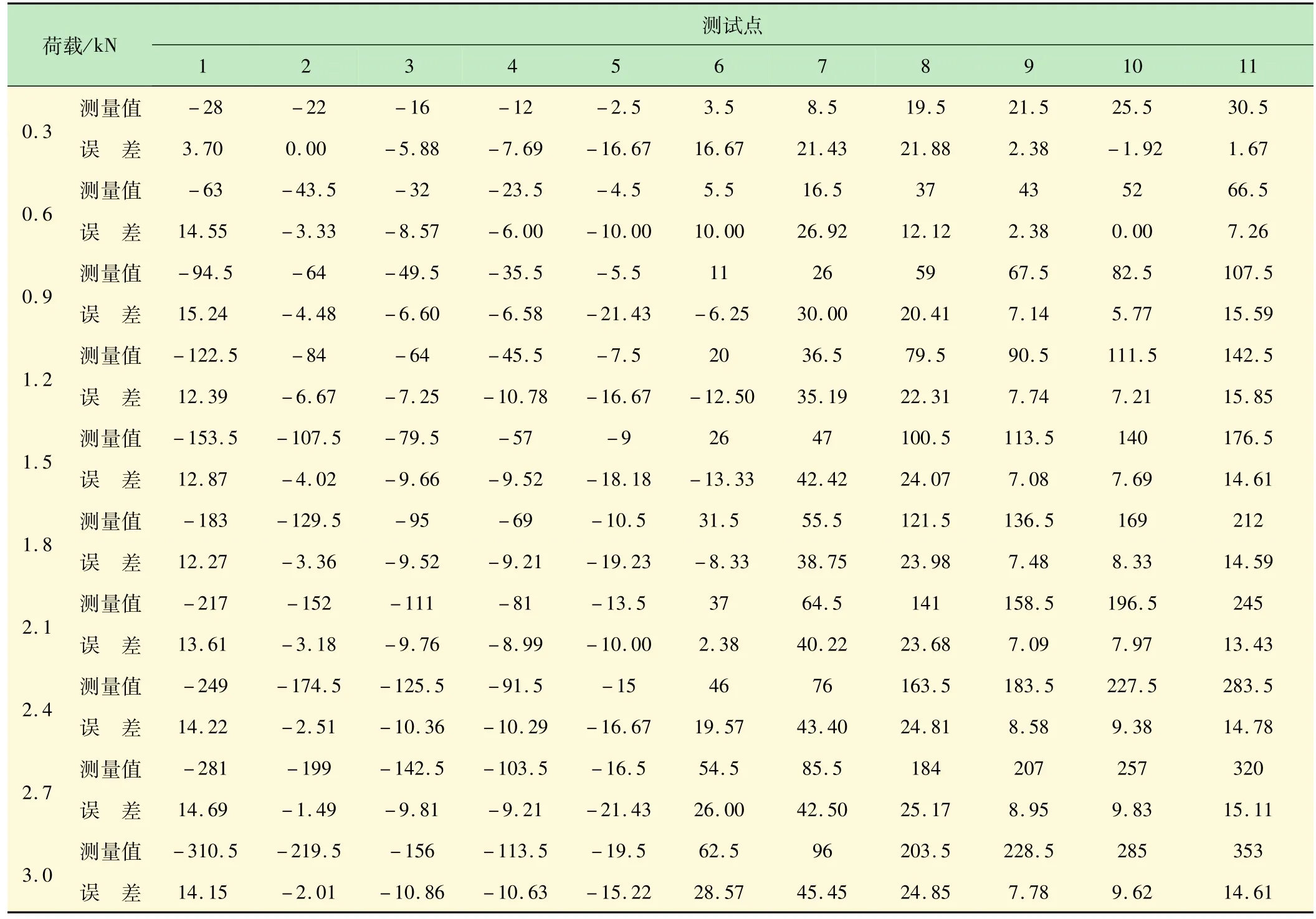
表2 第2组层合梁应变测量值(10-6)与测量误差 %
3 结 语
本文对3层材料层合梁纯弯曲问题进行了实验测试和分析,结果表明层合梁平面假设的有效性。上述内容可以与材料力学纯弯曲梁的弯曲实验与复合材料力学中关于梁的理论教学相结合,培养学生分析、解决力学问题的实践创新能力,为传统材料力学实验教学提供参考。

