在几何问题教学中培养学生多视角思维
江苏省盐城市射阳外国语学校 陈素兰
现在大多数学生用一种方法解答出题目后,不再考虑其他途径,导致这种现象的原因为思维长期受到束缚,只重结果,忽略了过程,从而忽视了一题多解与多变的意义,尤其在几何部分,在教学中教师需及时地引导和锻炼学生,全面提高学生的综合素质,学生具有的发展空间很大。
一、一题多解中求同性思维
在学习平面几何这块知识的时候,很多学生仅了解并掌握教材中的基本知识,对于解题的方法和思路却没有深挖,思考问题的思维往往易受到固定思维的限制,从而不利于教学的实施,教师可在课堂的例题中采用一题多解的解题方法来培养学生思考问题的求同性思维,有效解决数学问题。
例如,已知在四边形ABCD中,∠A为60°,∠B与∠C均为直角,且CD长为a,AB长为b,求BC的长。学生在做这种题型时,最常见的是两种方法:一种是作延长线,一种是作垂线。学生在拿到这种题型不知如何着手时,教师可以引导学生,让学生自己作辅助线解题。延长AD交BC于M点,因为∠A为60°,∠B为直角,则三角形ABM为直角三角形,AM长度为AB的二倍,DM长度为CD的二倍,BM和CM长度均能求出,则就可得出BC的长度。学生解到这里的时候就可以再次提问了,询问有没有其他方法可以解答,学生再次思考,如果学生通过第一种方法已经理解了这道题的精髓,就会想到过D点向AB作垂线,从而也能得到同样的结果。
上面这个例子可以很好地反映出求同性思维,采取多种途径得到所需结果。在一题多解中,教师逐步引导,抓住核心,有效地激发学生潜在的思维,锻炼学生的求同性思维,可使学生的思维更加条理化、逻辑化和严密化,因而实现教有所长,学有所得,当然整个过程中也需对学生表扬鼓励,让学生朝着更好的方向发展。
二、一题多解中求异性思维
对于数学这个科目,其核心素养是培养学生学习知识的能力,因此在教学中需要对几何知识点以点带面,逐步加深,并可采用一题多解,看是否有更好的解题方法选择,打开学生思维定势,多角度分析问题,激活学生的求异性思维。
例如,在三角形ABC中,CD为AB的中线,且CD为AB的一半,求∠ACB为直角。学生在拿到这个题目的时候,应该首先第一反应是求∠ACB为直角,即证三角形ABC为直角三角形,且直角三角形斜边上的中线等于斜边的一半。这题就可通过题目所给边的关系入手,再得出角的关系,最后根据等边对等角和其内角和为180°,即可得出结论。教师在这里还可以再次引导学生,可建议学生通过圆的知识点来解答,通过圆建立关系式,由直径到圆周角,再到直角三角形,即可推导出结论。
第一种解法为常规解法,学生顺利得出结果只能说明针对这块知识点掌握不错,多次练习可提高这块知识点的熟练度。但第二种解法就很巧妙,能很好地反映出对初中几何知识点的整体掌握,多角度思考,找出问题的本质。
三、一题多变中创造性思维
解题中培养学生的创造性思维,是在学生对教材中知识点了解及掌握的前提下进行的,是对知识点进一步的升华,创造性思维将贯穿整个数学学习阶段。因此教师可在几何教学中科引导学生善于发现问题,分析问题并从多角度运用所学知识解决问题。
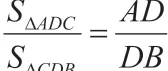
首先可以由简单的几何知识点引出,如线段、角度等,接着用三角形的有关性质和方法,这块知识点是学生原有认知中熟悉的知识模块,应很容易,最后再上升难度,升华一下 。这种由一题多变的方式即让学生复习了旧知识点,学会将不同知识点联系起来,同时还可让学生体会到一道题原来可以有这么多的创造,培养学生的创造性思维,懂得灵活应用。
总之,在数学教学中注重学生掌握知识点的同时要培养学生的思维习惯,一题多解及一题多变就是很好的途径,不仅可以激发学生的学习兴趣、理清知识体系、提高解题效率,对学生思维能力也能得到很大的提高。培养学生多视角的思维,重在平时教育教学中的渗透,教师要持之以恒。

