Franc3D 裂纹扩展计算中初始裂纹的参数确定

李 岩 冯永志 丁继伟 石多奇

（1、哈电发电设备国家工程研究中心有限公司，黑龙江 哈尔滨150028 2、北京航空航天大学能源与动力工程学院，北京100191）

涡轮盘承受着离心力和温度引起的复杂载荷。载荷和几何特征共同决定了轮盘上的多为复杂的复合型裂纹扩展。基于franc3d 的裂纹扩展分析已广泛应用[1-3]。国内许多学者已进行了Franc3D 准确性验证工作，证明其是裂纹扩展和寿命预测的可靠手段[4-8]。关于初始裂纹位置选取、初始裂纹尺寸和形状假设的相关报道很少。

本文基于静强度计算分析了涡轮盘的Mises 应力及周向和径向应力分布情况，确定了该轮盘的裂纹关键位置点；参考无损检测的统计结果假设裂纹尺寸。正确的选择和假设裂纹的位置和尺寸是获得准确寿命预测的前提。

1 裂纹位置确定

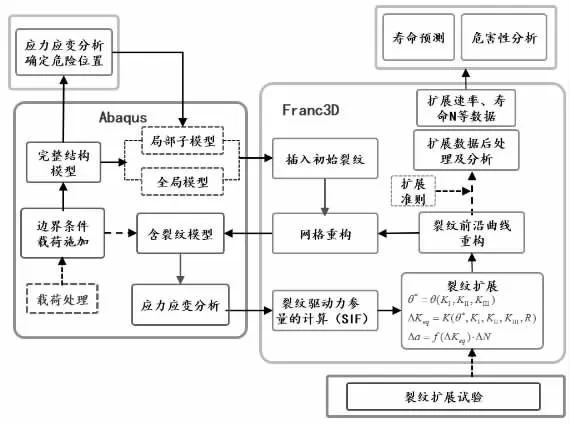
图1 裂纹计算原理流程示意图

要进行涡轮盘的裂纹扩展模拟，则需要进行静强度计算确定工作状态下轮盘容易萌生裂纹的位置。首先，通过MISES 应力初步判断可能的裂纹位置[9]。图2（a）所示，该轮盘榫槽底部MISES 应力最大、盘身两处圆角位置和中心孔的应力水平较高，这些是最可能出现裂纹的位置。其次，通过径向应力分布分析，进一步判断裂纹可能的位置。如图2（b）所示，盘身的两处圆角位置径向应力高，应力在900MPa 左右，也是可能出现裂纹的位置，该位置裂纹面法向与径向重合。再次，通过周向应力分布分析，更进一步判断裂纹可能的位置。如图2（c）所示，周向应力分布较为均匀，应力水平600MPa 左右，该处承担较大离心力盘，也是可能出现裂纹的位置，该位置裂纹面法向与周向重合。最后，结合表1，可认为通过静强度计算的应力分布判断的裂纹位置的假设是可能的。当应力计算结果出现超过材料在该温度下的屈服时则需要进行弹塑性分析[9]，例如本文轮盘榫槽底部。对于根据圣维南原理[10]，我们可认为该处的局部高应力并不影响对盘身位置的应力分析。线弹性假设仍适用于盘身裂纹初始位置的判定。

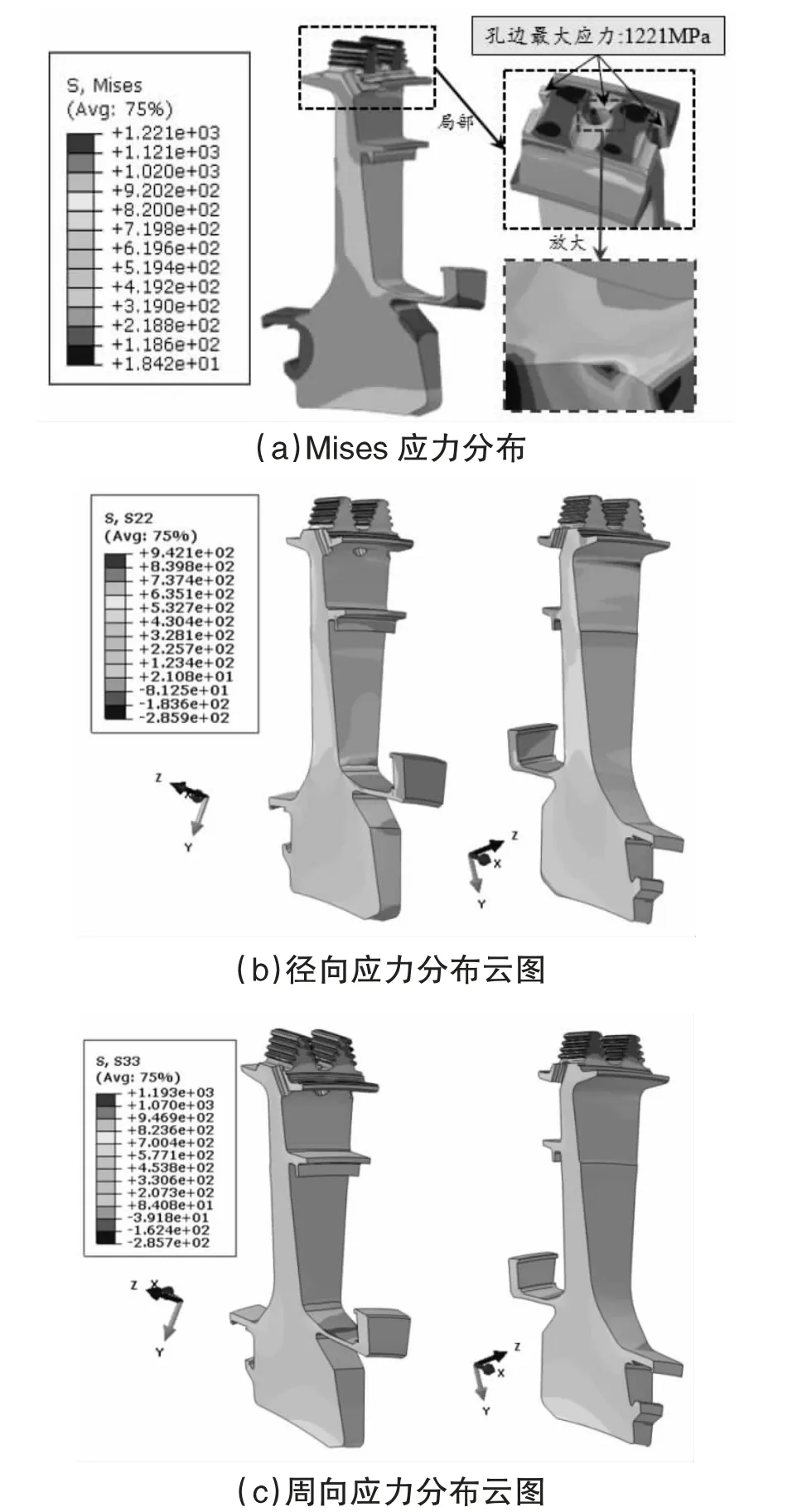
图2 线弹性等效应力云图

表1 盘类零件故障模式及成因[11]

2 初始裂纹尺寸设置

实际轮盘的裂纹形貌是复杂多样的，对于形式多样复杂的裂纹，在仿真计算过程中不能一一重现，需要对这些裂纹进行简化处理，使得结果向有利于轮盘安全性设计的方向进行。对于裂纹形状的简化，可以将任意形状的表面裂纹简化为半圆形或椭圆形片状裂纹，可以将任意形状的角隅裂纹简化为四分之一圆形片状裂纹，可以将任意形状的内部裂纹简化为圆形或者椭圆形片状裂纹。当轮盘裂纹已经过较长时间扩展，深度较深时，可简化为穿透裂纹。例如图2（a）中，轮盘榫槽底部最大Mises 应力出现在圆孔的边缘采用角偶裂纹；图2（b）中，盘身的两处过渡圆角位置采用半椭圆或半圆表面裂纹。

在轮盘损伤容限中，将轮盘服役前或服役过程中极少可能超过的裂纹尺寸作为初始裂纹尺寸。一般情况下，会按照轮盘设计准则、固有缺陷分布和制造及服役过程中使用的无损检测技术确定初始裂纹尺寸。目前无损检测技术可检最小裂纹尺寸情况如表2 所示。

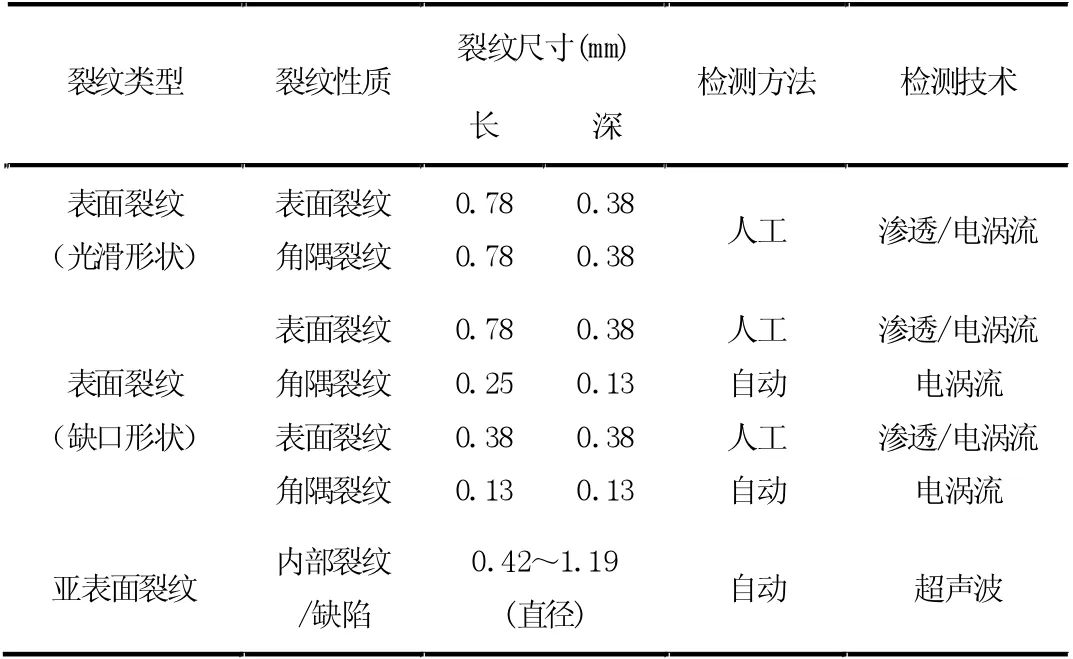
表2 无损检测技术可检最小裂纹尺寸[11]

当使用了更加先进有效的无损检测技术，或者在生产和维修中特别增加了许多高精度检测仪器，也可以假设更小的初始裂纹尺寸。美军标中半椭圆裂纹的尺寸为0.78mm×0.38mm，角偶裂纹半径尺寸为0.38mm[12]。轮盘的初始裂纹尺寸与夹杂尺寸有关，如某型压气机轮盘材料夹杂尺寸为100μm 左右，根据目前无损检测技术水平，可以假设轮盘初始裂纹为0.1mm。可见初始裂纹的尺寸受多方面的因素影响，为了尽可能模拟轮盘裂纹扩展的全过程，可以设置的初始裂纹尺寸比一般无损检测技术可检出最小裂纹尺寸更小。

3 结论

以断裂力学为理论基础的裂纹扩展分析和剩余寿命预测是损伤容限的核心，能够准确地判断危险位置和合理假设裂纹尺寸和形状是准确预测剩余寿命的前提。

通过Mises 应力、周向应力、径向应力分析能够有效判断裂纹的危险位置和初始裂纹面方向；结合无损检测的统计结果能够确定初始裂纹的半径尺寸；根据危险位置处轮盘的几何形状能够确定初始裂纹的形状。这是裂纹扩展分析的关键步骤，是开展某型燃气轮机第一级轮盘裂纹扩展特性及危害性分析的前提，只有当裂纹的位置和形状更加接近真实情况，才能准确预测剩余寿命。