基于API函数序列的勒索病毒家族同源性研究
岳 婷, 蔡满春, 芦天亮
(中国人民公安大学警务信息工程与网络安全学院, 北京 100038)
0 引言
近年来,勒索病毒一直处于猖獗态势,给企业和政府部门带来了不可估量的损失。CNCERT2018报告[1]称,伴随“勒索软件即服务”产业的兴起,活跃勒索软件数量呈现快速增长势头,且更新频率和威胁广度都大幅度增加,变种数量不断攀升,对重要行业关键信息基础设施的威胁加剧。据Malwarebytes发布的《2019年勒索软件回顾报告》[2],勒索病毒攻击将重点从消费者转移至企业,针对企业的勒索病毒攻击数量首次超过了针对消费者的数量,前者在2019年第二季度比2018年第二季度增长了363%。《2019年SonicWall网络威胁报告》[3]显示,全球勒索病毒攻击增加了15%,Cerber家族仍是黑客攻击企业最常采用的勒索病毒。因此,对勒索病毒的分析和研究尤为重要和迫切。
根据学界对恶意代码同源性的理解[4],加之勒索病毒是恶意代码的一个分支,给定本文的同源性研究是针对同一家族勒索病毒的同源性,即通过勒索病毒家族特征分析家族的同源性。由于勒索病毒的家族特征,每个家族又会衍生出不同版本的变种,因此,同一家族的勒索病毒与不同家族的勒索病毒之间在相似性上存在一定差异,有学者通过研究勒索病毒的演变和特征给出了证明[5]。最早将生物信息学上的多序列比对应用到恶意代码同源分析上的是官强[6],但其使用的是IDA Pro静态提取系统调用函数序列。随着勒索病毒的发展,强壳、花指令等使得通过逆向静态分析获取其行为特征越发困难,为了更加全面准确获取其行为特征,本文使用Cuckoo沙箱动态监测并提取API函数调用序列。
在使用生物信息学的序列比对方法研究恶意代码的同源性上,针对勒索病毒家族同源的研究较少,截至目前,只有文献[8]针对勒索病毒家族同源在序列比对方法上做了探究。总体来说,序列比对方法在恶意代码同源性研究的应用上,目前存在以下几个问题:(1)多使用ClustalX/W2系列多序列比对软件[7-8],目前的T-coffee 在多序列比对准确性上要优于ClustalX/W2系列[9];(2)通过多序列比对得出家族图谱时,一般是从样本中选择代表性序列[8,10-11]或者是共性水平为100%的共性序列[7],由于实验数据集家族样本在变种的数目和分布上的差异,可能会丢失某些重要的序列片段。目前,在对勒索病毒未知样本家族进行预测时,选择的是全局比对算法[8],由于勒索病毒实现某些行为是由API函数子序列片段实现的,因此,使用局部比对相较于全局比对在相似性计算上更有指导意义。针对基于序列比对方法的勒索病毒家族同源性研究,为了解决以上问题,本文综合了Multalin、Clustal Omega、T-coffee 3种方法分别进行多序列比对,并设置了不同的共性水平,通过计算,从中选出最佳共性序列代替从样本中选择代表性序列作为家族图谱序列,实验结果表明,使用最佳共性序列作为家族图谱序列且使用局部比对在区分不同的勒索病毒家族的效果上更佳。
1 研究思路
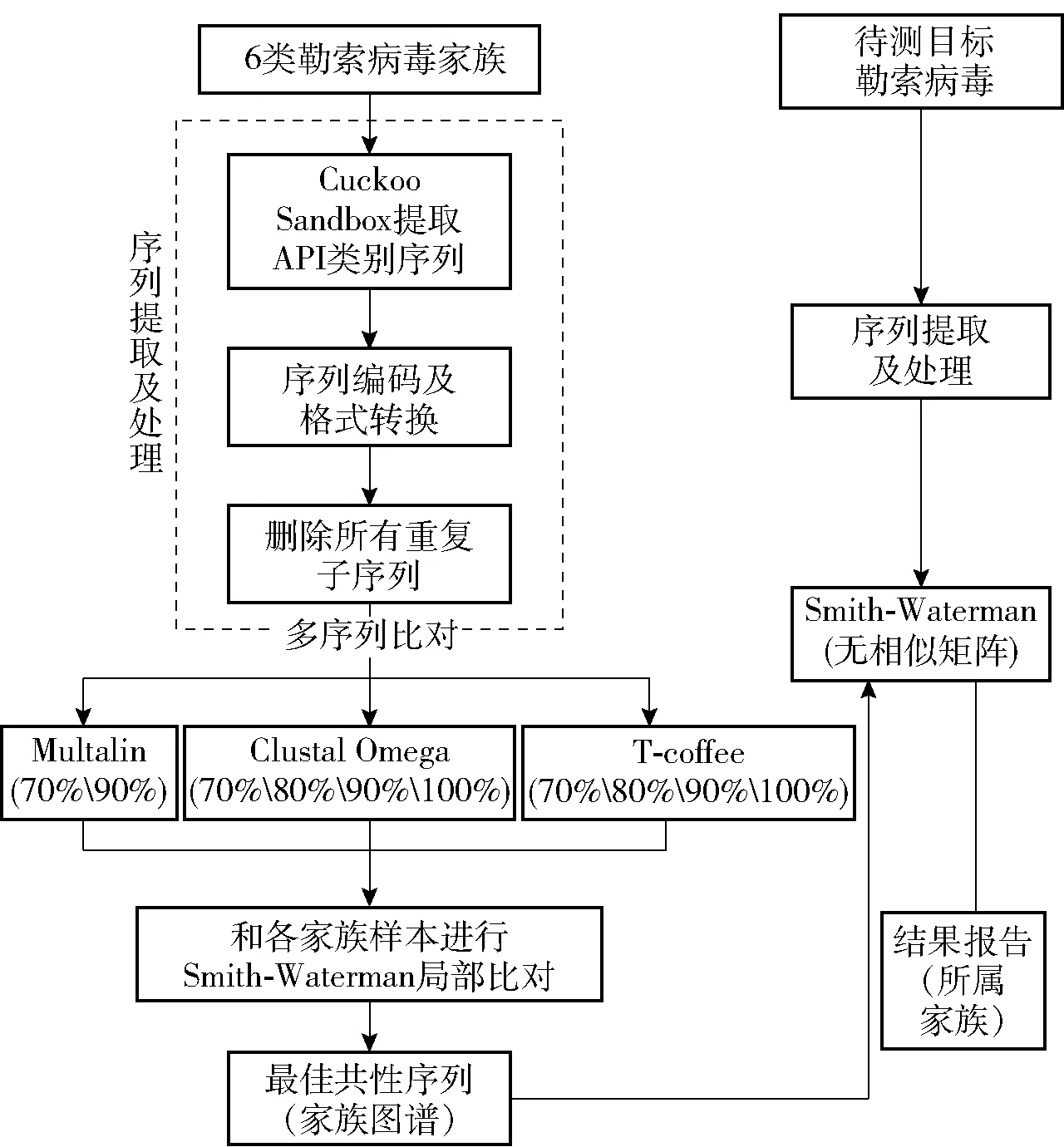
图1 研究思路整体架构
勒索病毒家族同源性研究思路的整体架构如图1,主要分成3个部分:一是序列提取及处理,先使用Cuckoo 沙箱自动化分析勒索病毒样本,监测其动态行为,提取API函数类别序列并对其进行编码,转化为fasta文件格式,在此基础上去除所有重复子序列;二是通过3种多序列比对方法,分别设置并提取不同水平的共性序列,通过局部比对,以“家族内相似性较高,家族间相似性低”为标准,择优选出最佳共性序列作为家族图谱序列;三是对已进行序列提取及处理的待测数据样本序列和家族图谱序列进行局部序列比对,通过计算得到相似性进行比较,进而对其所属家族进行判断。
2 API函数序列提取及处理
2.1 API函数类别序列提取及编码
因为静态分析使用的是已知恶意代码特征信息,难以检测到勒索病毒变种,且静态分析难以规避勒索病毒强壳、花指令等情况,因此本文采用动态分析的方法。Cuckoo sandbox是一款开源的自动化恶意软件分析系统,本文使用它在受控环境中跟踪和捕获勒索病毒动态行为,提取勒索病毒进程的API函数类别序列以表征其恶意行为。
由于某些勒索病毒存在反虚拟机制,在Cuckoo自动化分析过程中存在逃逸行为,通过实验观察,这类情况会导致Cuckoo分析中止、Cuckoo分析日志完整但分析报告不完整以及Cuckoo分析日志和分析报告均完整但未提取到API函数调用等情况,这类黑样本由于未提取到实验所需要的API函数类别信息,这里未予采用。
在Windows 平台上,勒索病毒实现某些特定行为,不可避免会使用到大量的API函数调用,因此分析系统API函数调用,可以分析和判断一个程序的行为[12]。但是由于API函数调用的种类繁多、数目较大,提取得到的序列长度不利于进行多序列比对,消耗的时间复杂度较高。结合Cuckoo行为分析报告,统计API函数调用类别,共计16类,具体见表1。因此,按照时间顺序提取API函数调用类别序列表征勒索病毒行为特征,并参考生物信息学上蛋白质序列的表示方法,使用英文大写字母进行编码。
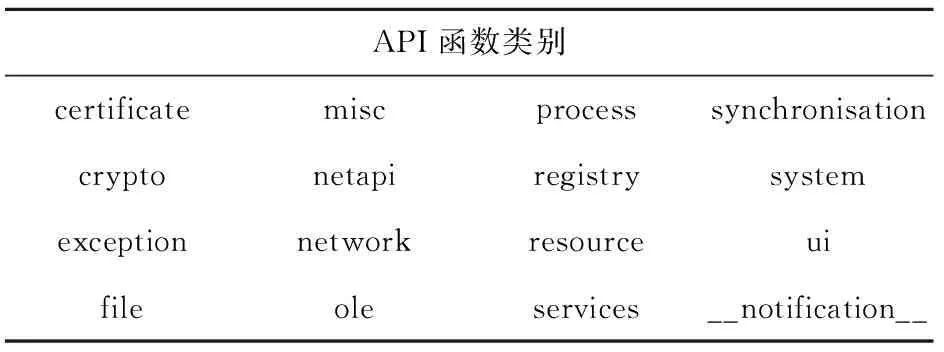
表1 API函数类别表
2.2 序列去重算法
由于勒索病毒在读写文件和加密文件等情况下存在频繁的调用模式,且重复次数可能根据环境差异也有所不同。此外,也有可能刻意添加频繁调用或无用代码以逃避检测。因此提取到的API函数类别序列存在着大量的重复子序列,因为序列比对算法对序列的长度敏感,会对对齐结果产生干扰,参考一些研究方法[8-11],这里设计了一种去除所有重复子序列的方法,研究表明,删除所有重复子序列不会损失总体精度。假设ls是需要去重的单条序列,DelRepeatSeq函数相应的伪代码如下:
Input: ls
Output: ls_afterrepeatdel
Begin
before_ls = ls.copy()
step←1; p_start←0
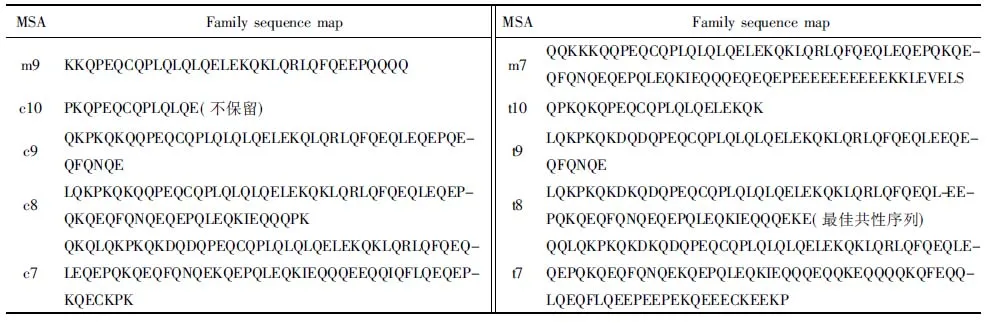
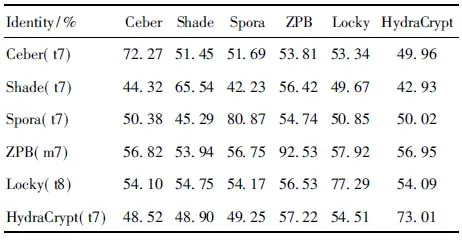
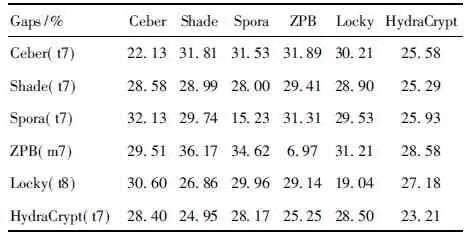
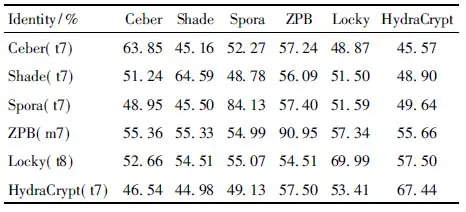
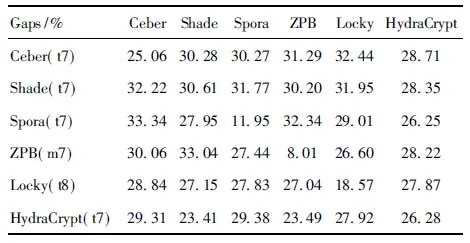
while step+p_start i←0 ∥如果剩余的元素小于步长,则可以停止循环 while ls_length-i>=2 * step do if ls[i:i+step]==ls[i+step:i+2 * step] del ls[i:i+step] ∥删除元素后,索引会改变 i←i-step len(ls)←len(ls)-step i←i+1 END while p_start←p_start+1 step←step+1 END while print(len(before_ls), len(ls)) ∥如果删除后的ls的和初始结果不同,再重新遍历一次 if ls == before_ls return ls else return DelRepeatSeq(ls) END 序列比对广泛运用于生物信息学,由于由相似的序列可以推断出相似的结构或相似的功能,因此可以通过检测未知序列与已知序列的相似性来确定未知序列的功能。参考生物信息学领域使用多序列比对提取图谱序列对未知样本序列进行判断的方法,这里针对不同家族序列使用多序列比对方法提取家族图谱序列,之前研究者[7-8]大多选用ClustalW,通过共性水平为100%的比对结果从样本中选择代表性序列或者共性序列作为家族图谱序列。由于各家族中都存在变种,变种的版本和数目在分布上也有所不同,因此选择共性水平为100%时,会导致无法获取某些子序列特征段,设置不同共性水平可以一定程度避免这个问题。本文选取了Multalin、Clustal Omega和T-coffee 3种工具[13-14],并且提取不同共性水平下的共性序列,共计10条,再通过计算比较从共性序列中得到最佳共性序列作为家族图谱序列,最终使用局部序列比对的方法对未知样本进行判断。 Multalin[13]是一种具有层次聚类的多序列比对方法,它首先通过双序列比对得出一个得分矩阵,根据矩阵中最佳得分对应的两条序列,依次进行层次聚类,直到序列的聚类不变,即序列比对完成。Clustal Omega[15]是Clustal系列的升级版,在原有的基于快速词成对对齐的基础上,使用时间复杂度为O(NlogN)的mbed算法,可以处理大数量级(数万个)的数据集;其次,改用隐马尔可夫模型(HMMs)对齐,大幅提高了精度。T-coffee[9]的基本原理是:首先进行预处理,分别使用ClustalW进行双序列全局比对和Fasta进行局部比对,构建库以整合比对结果信息,针对比对的每个元素综合库中相应的信息赋予合理的权重值,再进行渐进式序列比对。该方法的优势在于能够整合各种信息,可扩展性强,准确率高。但是时间复杂度为O(N2L2)+O(N3L)+O(N3)+O(NL2),比对速度较慢,适合于数据集较小(n<100)时使用。 双序列比对分为全局比对和局部比对。全局序列比对算法旨在对齐序列的每个元素,适合于比对两条序列相似且序列长度大致相等的序列。局部序列对齐算法更倾向于在整个序列中对齐某些相似的序列片段。参考局部序列比对的生物学基础,勒索病毒实现某个功能是由于某些特定的API函数序列来完成的,尽管在序列的其他部分可能存在一些操作的增删改动,但是这些序列段有一定的共性,在做未知序列判断时相比全局比对而言更具有指导意义。Needleman-Wunsch[16]算法和Smith-Waterman[17]算法分别是经典的全局比对算法和局部比对算法。这里重点对Smith-Waterman算法进行说明。 Smith-Waterman算法主要包括确定置换得分矩阵和空位罚分、初始化得分矩阵、计算打分和回溯4个步骤。假定两条序列A=a1a2a3…am和B=b1b2b3…bn,s(ai,bj)是序列A和B中元素ai和元素bj的相似性,Wk是在序列中插入长度为k时的罚分。 由于这里的API函数序列各个元素之间相互独立,不用考虑序列中元素之间的相似性量化关系,因此没有使用生物上的置换得分矩阵,空位罚分Wk=-5k。 初始化得分矩阵H首行首列: Hk0=H0l=0,0≤k≤n,0≤l≤m (1) 按照从左到右,从上到下的顺序进行打分,计算得到H: (2) (3) 最后从矩阵H中得分最高的元素开始回溯路径,直至遇到得分为0的元素,即得到最佳局部对齐。 在生物信息学[18]上使用一致度和相似度来衡量序列之间的相似性,由于不用像生物学那样考虑序列元素之间的相似度量化,因此只需考虑一致度即可。在序列比对中,一致度是指比对结果中它们对应位置上相同的元素数目占总长度的百分比。 设序列A,B匹配的结果中的元素数目为L,序列A或B中‘-’出现的数目为G,对齐后的长度(含空隙)为L_aligned,则序列A,B的相似性和空隙值为 (4) (5) 以序列“LQCQQKQQLKE”“LQCQLQELKQLQ-KLQE”局部对齐为例,对齐后的效果如图2。aligned是指sequen1和sequen2对齐后的结果,长度为12;匹配的元素数目即aligned不含空隙的长度,即为8;空隙值为“-”的个数,即为4。综上,得出图2对应的相似性和空隙值。 图2 示例比对结果图 通过设置不同共性水平的3种多序列比对方法得到10条共性序列之后,通过局部序列比对,进行相似性计算后,再参考方差计算方法,设N为勒索病毒家族种类数,X0表示共性序列与本家族样本的平均相似性,Xi表示共性序列与非本家族第i个家族样本的平均相似性。取M最大的序列作为本家族最佳共性序列,公式如下: (6) 本文使用的勒索病毒家族样本采用公开数据集(http:∥www.malware-traffic-analysis.net/),为了确保实验数据无污染[19],勒索病毒样本数据集均上传至Virus Total网站进行检测分析,并选择44家以上报毒且5家以上报出对应家族名称的样本作为实验数据集。最终使用的实验数据集情况如表2,其中6个家族勒索病毒共计96个。为了数据表示方便,Zeus Panda Banker在后文中简称为ZPB。 表2 实验数据集情况 对于勒索病毒实验数据集,通过搭建Cuckoo Sandbox沙箱虚拟环境对其进行自动化分析,实验搭建的具体环境如下: 4.2.1 对比实验设置 表3 沙箱监测实验环境 为了验证本文提出的综合多种多序列比对方法使用最佳共性序列作为家族图谱序列,并使用局部比对方法对未知勒索病毒家族进行判断的方法有更好的效果,设置了两组对比实验,均采用控制变量法。第一组实验中,家族图谱序列使用现有研究中多使用的ClustalX/W2系列方法中最新的Clustal Omega方法得出的家族样本代表序列,分别使用全局比对Needleman-Wunsch算法和局部比对Smith-Waterman算法对家族样本代表序列和各家族样本序列进行相似性计算,设定家族样本代表序列与各家族样本序列的相似性平均值为该家族图谱序列与各家族的相似性,通过该相似性的比较确定效果较佳的双序列比对算法。第二组实验,根据第一组实验所确定的双序列比对方法,设置变量为家族图谱序列的选择,分别使用家族样本代表序列和最佳共性序列作为家族图谱序列,家族样本代表序列选定为某家族中确定为最佳共性序列所使用多序列比对方法结果中的参考性序列,如图5中的reference sequence,然后通过所确定双序列比对方法计算相似性,进而对方案的有效性进行验证。 4.2.2 实验结果及分析 从6个勒索病毒家族96个勒索病毒样本的Cuckoo报告文件中提取对应勒索病毒进程的API函数类别序列,并使用序列去重算法对其进行处理,以Spora-bc799544a序列为例,删除所有重复子序列前后的数据大小和数据内容的变化如图3和图4所示。 图3 Spora-bc799544a序列去除重复子序列后的数据大小变化 图4 Spora-bc799544a序列去除重复子序列后的内容变化 第一组实验中,使用ClustalX/W2系列方法中最新的Clustal Omega方法,并设置共性水平为100%,取各家族多序列比对结果中的参考序列为各家族样本代表序列,分别使用全局比对和局部比对进行相似性计算,结果如表4和表5所示。 图5 Locky家族样本使用T-coffee得出的四条共性序列(部分) 表4 使用家族样本代表序列和全局比对结果 表5 使用家族样本代表序列和局部比对结果 通过全局比对和局部比对的实验结果可知,局部比对在6个勒索病毒家族上的结果均优于全局比对结果,且表现更为稳定,因此在对未知勒索病毒家族进行判断时选择局部比对算法更佳。 由第一组实验确定了在第二组实验中使用局部比对方法,实验二在进行多序列比对时,设置Multalin序列比对结果的共性水平为70%和90%(分别记为m7和m9,下同),Clustal Omega和T-coffee分别为70%、80%、90%、100%,一共10条共性序列。以T-coffee处理Locky家族序列为例,得出的4条共性序列(部分)如图5所示。 Locky家族的10条共性序列见表4,考虑到家族序列的全局性和功能的综合性特点,对于集中出现在一个位置且本身长度较短(低于15)的共性序列未予保留。剩下9条有效序列和6个家族的勒索病毒样本序列分别进行Smith-Waterman局部比对,最后与每个家族样本比对的结果取平均值作为Locky家族图谱序列与该家族的相似性,通过公式(1)计算得出t8所对应的序列为该家族的最佳共性序列。 表6 Locky家族的10条共性序列 确定某一家族最佳共性序列后,取确定为最佳共性序列所使用的多序列比对方法对应的家族样本代表序列和最佳共性序列分别作为家族图谱序列,与各家族样本局部比对结果的平均值作为该家族图谱和各家族之间的相似性,相似性结果如表7~10所示。 表7 各家族图谱与各家族之间的相似性 表8 各家族图谱与各家族之间的Gaps值 由表7~8可得,表7中各家族的最佳共性序列与本家族样本序列的平均相似性均明显大于与非本家族样本序列的平均相似性,同一家族勒索病毒的同源性概率较大。整体上看,T-coffee多序列比对算法用于提取共性序列的效果最佳,这得益于它先通过整合全局和局部比对构建比对库,也验证了T-coffee准确率高于ClustalX/W2系列的结论[9]。表8中,平均Gaps值在个别样本上表现出同一家族样本Gaps值小于和接近非同一家族样本序列Gaps值,区分性不如相似性明显,可以认为在区分勒索病毒家族时Gaps值可以起参考作用。由于勒索病毒家族之间也存在一些相似的恶意行为,如读写文件、加密文件等使得不同家族之间也有一定的相似性,家族内部样本变种的数目和分布存在差异对实验结果也有一定影响。 表9 各家族样本代表序列与各家族之间的相似性 表10 各家族样本代表序列与各家族之间的Gaps值 由表9~10可得,选择各家族样本代表序列作为图谱序列时,同样表现出与本家族样本序列的平均相似性均明显大于与非本家族样本序列的平均相似性,但是在和表7中的结果进行比较时,除Spora家族外,与本家族样本序列的平均相似性结果均低于表7中的结果。可以认为,通过选取最佳共性序列作为家族图谱序列的方法可以结合数据集样本的更多特征,总体上要优于选择家族代表样本序列的方法。表10中,平均Gaps值和表8中均表现出与本家族的结果高于与非本家族的情况,差异不大。 综上,可以得出结论,通过选取最佳共性序列作为家族图谱序列,并使用局部比对进行相似性计算的方法可以更好地对勒索病毒家族进行区分。 本文在研究勒索病毒家族同源性时,通过使用Cuckoo沙箱动态行为监测并提取API函数类别序列,设计删除所有重复子序列的方法避免后期多序列比对时的对齐干扰和时间消耗。为了得到更多的序列特征,通过3种多序列比对方法,设置不同的共性水平,提取并计算得到最佳的共性序列作为家族图谱序列。经实验验证,局部比对相较于全局比对更适宜于勒索病毒家族同源性研究,最佳共性序列相比较于家族样本代表序列更具有代表性,使用最佳共性序列作为家族图谱并使用局部比对计算相似性可以更好地对勒索病毒家族进行区分。3 序列比对算法
3.1 多序列比对
3.2 双序列比对
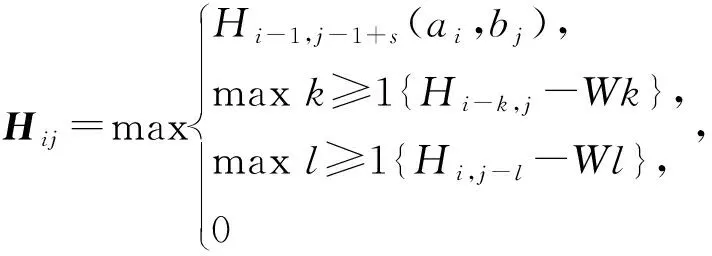
3.3 相似性计算方法及最佳共性序列确定方法
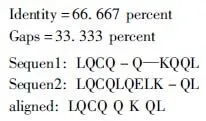
4 实验验证及分析
4.1 实验数据集

4.2 实验设置与结果


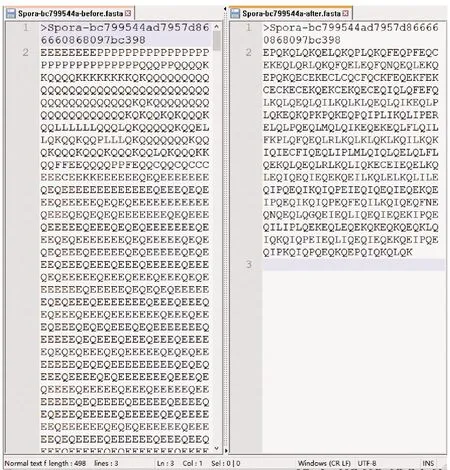
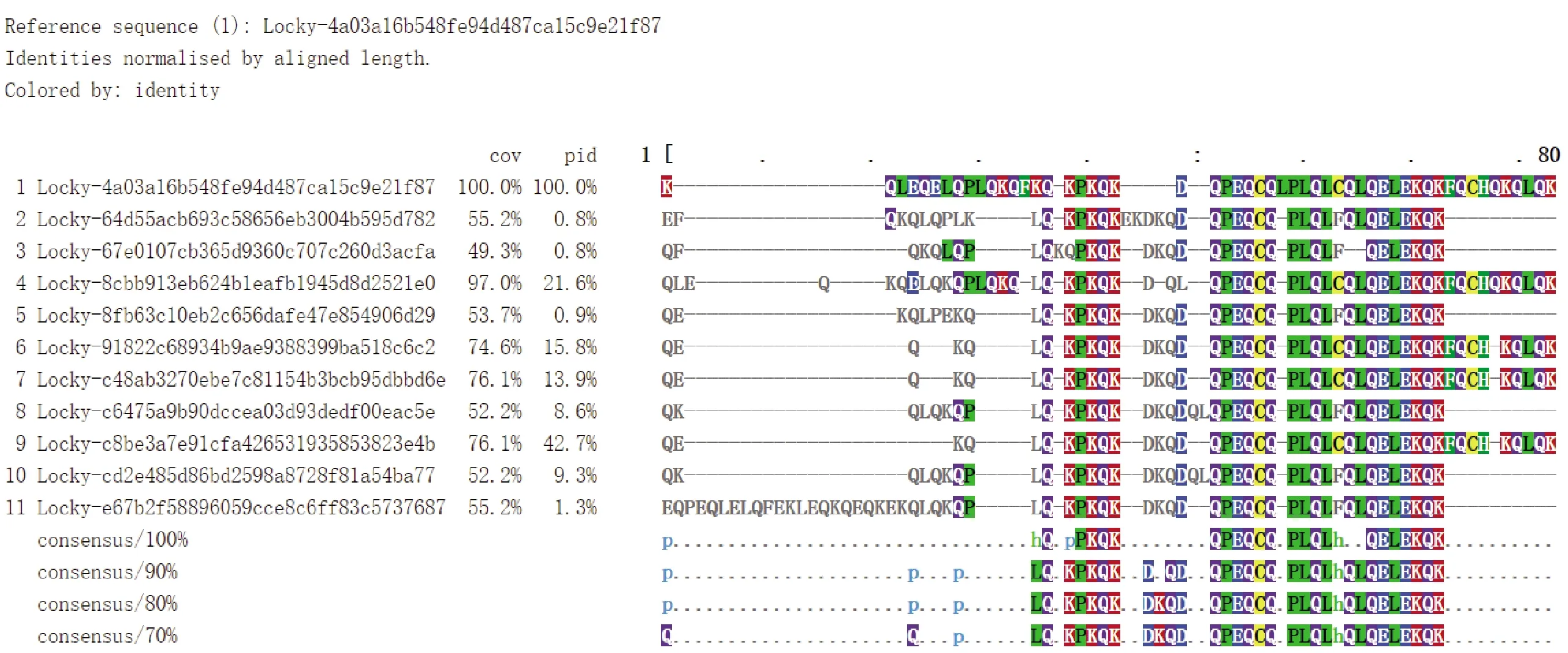
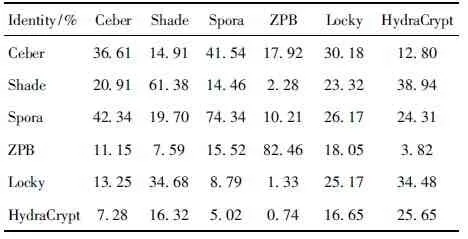
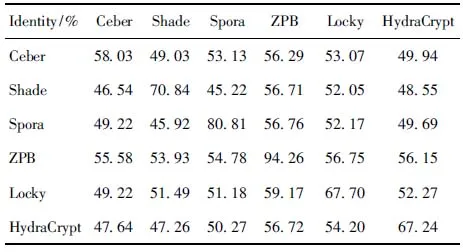
5 结语
——美创科技“诺亚”防勒索系统向勒索病毒“宣战”

