基于聚类分析的道路交通事故多发点段评价方法

常安德， 张朝旭， 陈 松

(1.公安部痕迹检验鉴定技术重点实验室， 辽宁沈阳 110035; 2.中国刑事警察学院， 辽宁沈阳 110035)

0 引言

随着机动车保有量、驾驶员数量及道路里程的不断增加，道路交通安全问题已成为我国最严重的社会难题之一。2018年，我国汽车发生交通事故166 906起，导致46 161人死亡，169 046人受伤，直接财产损失118 671.6万元。从数据总量来看，我国道路交通事故预防工作的形势依然非常严峻。

如何通过深挖历史积累的大量道路交通事故数据，提取交通事故发生的时空特征，发现交通事故多发点段，分析交通事故成因规律性，评价事故多发风险等级，进而制定更具针对性的交通事故预防措施，显得意义重大。

多年来，学者一直在对道路交通事故多发点段(或黑点)的分析评价开展研究工作。孙平等采用累计频率法对交通事故多发点段进行鉴别，并针对天气因素建立交通事故概率模型[1]；肖慎等采用一种类似质量控制法的方法，计算出道路各特征的综合影响强度事故率临界值[2]；耿超等按照相邻原则对道路点段进行动态划分，并利用DBSCAN算法对事故多发点段进行评价[3]；严亚丹等针对高速公路运用事故数法对事故多发点段进行识别，并运用贝叶斯方法计算出事故影响因素的概率值[4]；孙连超等提出了一种基于TCT的灰色评价法，为事故多发点段的鉴别提供了新思路[5]；杨轸等提出一种双曲正切函数替代双指数函数的事故多发点段鉴别方法[6]；谢华为采用当量总事故次数法对沈海高速公路上的隐患路段进行鉴别[7]；王建等提出灰色聚类评价的事故多发点段鉴别方法[8]。上述研究对于交通事故空间点位信息考虑不足，导致道路交通事故多发点段评价的可靠性有待提高。

为此，将在定义道路交通事故多发点段和充分考虑交通事故空间定位信息的基础上，基于聚类分析技术研究一种道路交通事故多发点段的识别方法，同时设计一种事故多发点段空间范围的动态非定长划分方法，进而利用当量总事故率法将交通事故多发点段划分为3个风险等级，并给出具体的划分标准。

1 道路交通事故多发点段的识别方法

利用交通事故的空间点位信息鉴别交通事故多发点段最重要的是精准确定交通事故的点位。在欧美发达国家是在交通事故处理现场进行空间自动定位，我国目前是采用传统的“道路名称+里程桩号”以及事故地点信息描述的形式对交通事故进行定位[9]。

系统聚类分析方法的思想是通过交通事故发生的空间点位信息，对交通事故之间的距离进行计算，先将发生的交通事故各自归为一类，再将根据距离公式计算出的距离最近的两起交通事故聚为一类，以此类推，从而把路段上的所有交通事故聚成一类。

1.1 距离测度

距离测度的出发点是定义空间中点与点之间的距离，距离越近的点，相似程度越高，在聚类时更可能归为一类。系统聚类中，在度量样本与样本之间的距离时，一般使用的距离有欧氏距离、绝对值距离、明科夫斯基距离、马氏距离和兰氏距离。

欧氏距离是两个点在维度空间中的真实距离，同时也是聚类分析中用的最广泛的距离；绝对值距离使用时它假设变量之间是不相关的，如果变量之间是相关的，则聚类结果不可信；明科夫斯基距离是一个通用的距离测度公式，由它可以转变成绝对值距离和欧氏距离；马氏距离表示数据的协方差距离，所以受协方差矩阵不稳定的影响，总是夸大了变化微小的变量的作用而不能顺利地计算出结果；兰氏距离虽然克服了量纲的影响，但是没有考虑到指标间的相关性。

考虑到交通事故的空间点位信息及其特点，本文选择使用欧氏距离来计算事故点位之间的距离。欧氏距离定义为：

其中，dij表示点i与点j之间的距离，xik表示第i个点在第k个变量上的值。

1.2 系统聚类分析方法

在系统聚类中，度量数据之间的亲疏程度是极为关键的，每一种距离测度都对应相应的聚类分析方法，衡量样本数据与小类、小类与小类之间亲疏程度的度量方法主要有组间联接法、组内连接法、最近邻元素法、最远邻元素法、质心聚类法、中位数聚类法和瓦尔德法7种。

不同的聚类分析方法表示不同的类与类的距离计算方法，各种方法的聚类结果不一定完全相同，但一定大致相似。其中组间联接法和瓦尔德法是最常用的两种方法，所以本文选择使用组间联接法对交通事故点位进行聚类。

2 聚类分析技术的过程和结果

对交通事故数据进行聚类和分析是通过SPSS工具进行的，SPSS是大型通用专业统计分析软件，该软件能够利用多种类型的数据文件和数据来源，生成统计报表和统计图形，从而进行简单和复杂的统计分析。

2.1 聚类分析过程

根据SPSS软件的数据分析步骤，把交通事故数据整理到相应的文件类型中，并对数据进行预处理，然后把数据导入SPSS软件中。

利用软件工具栏中的分析功能，选择分类中的系统聚类方法，把变量导入变量框内。

在统计中设置解的范围，根据对数据的预期设置最小聚类数和最大聚类数；在图中设置显示谱系图，进而很直观地看到数据聚类的过程；在方法中设置聚类方法和距离测度，聚类方法选择组间联接法，距离测度选择欧氏距离。如图1、图2和图3。

图1 设置解的范围

图2 设置谱系图

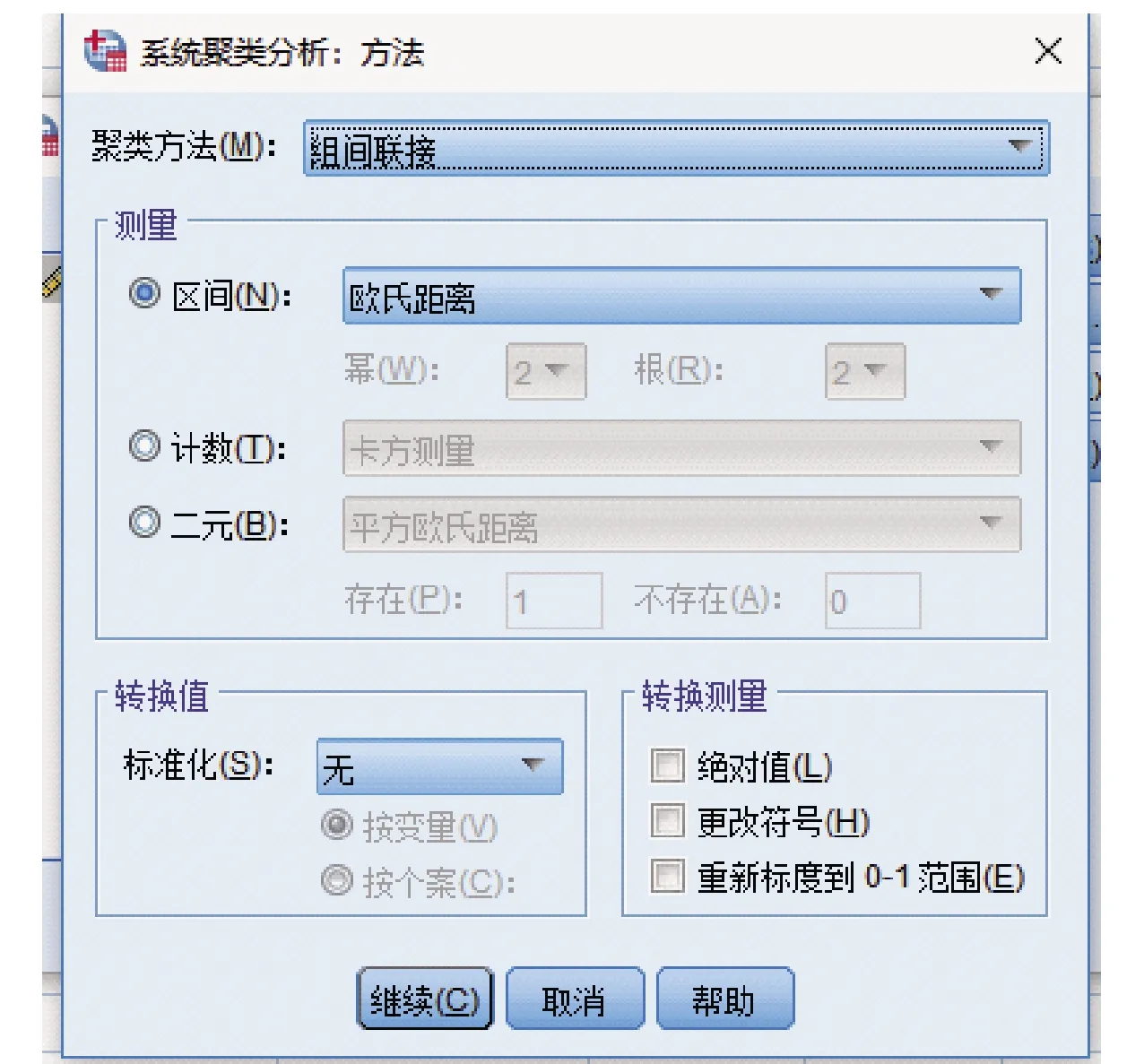
图3 设置聚类方法和距离测度

2.2 聚类分析结果

根据以上设置的聚类分析过程，数据的聚类分析结果可有聚类成员、谱系图和冰柱图3种显示方式。

聚类成员是以表格形式显示聚类结果，虽然浅显易懂，但是当数据量大时，结果就不太容易观察了；谱系图将聚类结果以树的形式直观的展示出来，形象生动，简单易懂，是聚类分析结果最常用的可视化形式；冰柱图能够反映系统聚类的每一步过程，也是聚类分析结果的一种重要形式。

3 事故多发点段空间范围动态非定长划分方法

定长划分方法虽然具有一定的可行性和很好的操作性，但是会存在精准性差的特点。如果把不发生交通事故的道路划分到事故多发点段内，就会造成后期资源的浪费。所以需要提出一种没有长度限制、动态变化的点段划分方法。参考已有研究对交通事故多发点段的定义和划分，将道路的最小单元长度定为400 m[10]，依据2019年公安部交管局印发的《公路交通事故多发点段及严重安全隐患排查工作规范(试行)》，将道路的最大单元长度定为2 000 m。根据相邻原则，如果下一单元道路长度内有事故发生，则划分到上一点段长度内，直到点段达到最大长度为止。具体的划分流程如图4所示。

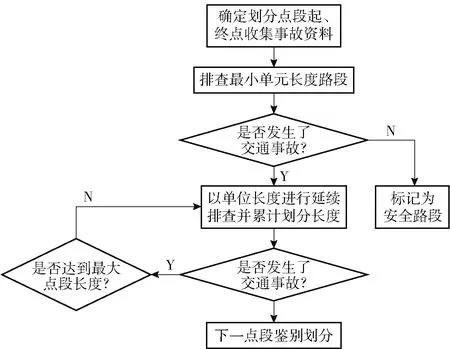
图4 事故点段动态非定长划分流程

4 交通事故多发点段风险等级评价方法

道路交通事故多发点段评价的目的是要找出危险度最高的点段，来为交通事故预防提供决策依据。目前，交通事故多发点段评价方法主要有事故数法、模糊评价法、层次分析法、概率统计法、BP神经网络法等。本文考虑方法的实用性，采用基于当量总事故率的方法来对交通事故多发点段进行评价。

4.1 评价指标建立

当量总事故率法是在当量总事故次数的基础上考虑事故率影响，进而确定事故多发点段的危险性大小。

当量总事故次数是在事故多点段处通过对总事故数、死亡人数和受伤人数赋以不同的权重值来计算得出。具体的计算公式为：

A=k1x1+k2x2+k3x3

(1)

式中：A表示当量总事故次数；x1、x2和x3分别表示总事故数、死亡人数和受伤人数；k1、k2和k3分别表示总事故数、死亡人数和受伤人数的权重。

建立基于当量总事故率的方法评价交通事故多发点段模型时，引入日平均交通量作为指数，事故率作为鉴别事故多发点段的指标。当计算出当量总事故次数A后，从而得出：

(2)

(3)

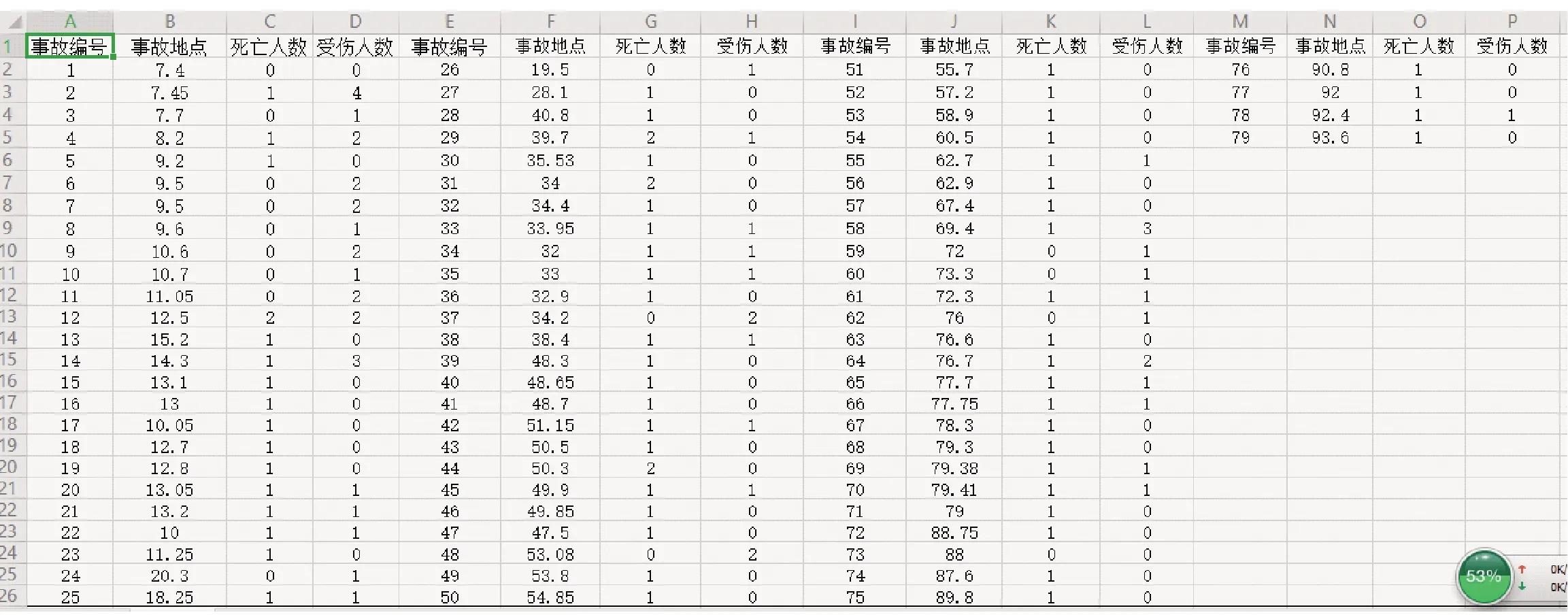
图5 2015～2018年该道路交通事故数据图

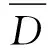
4.2 风险等级划分

鉴别交通事故多发点段的目的是预防交通事故，降低事故发生所造成的伤害。对交通事故多发点段的危险程度进行划分，等级越高表示危险度越高，治理的紧迫性越强。通过事故多发点段的等级评价给交管部门优先治理哪些事故多发点段提供参考。道路事故多发点段危险度划分如表1所示。

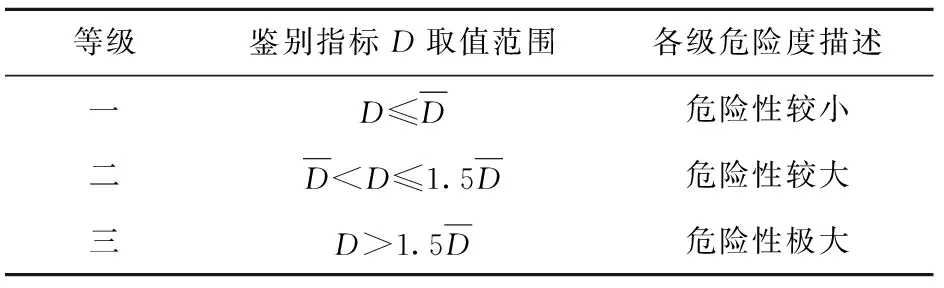
表1 道路事故多发点段危险度划分及描述

5 实例分析

针对某市内某条公路80 km路段2015～2018年发生的交通事故数据进行汇总。此公路日平均交通量约1.3万次，统计年限内共发生交通事故79起，死亡67人，受伤54人。具体交通事故数据如图5所示，在奥维地图上对应的交通事故空间点位分布如图6所示。采用基于聚类分析的方法对交通事故多发点段进行评价。

图6 2015～2018年该道路交通事故点位分布图

5.1 交通事故多发点段鉴别

根据聚类分析方法，将交通事故数据导入SPSS软件中，运用类间平均链锁法和欧氏距离测距法，设置最小聚类数为10，最大聚类数为20，得到聚类结果如图7所示。

图7 交通事故点位聚类结果

根据聚类结果，结合道路的实际情况对比各种不同的聚类数，发现聚成20类的效果最好，所以得到交通事故多发点段如表2所示。

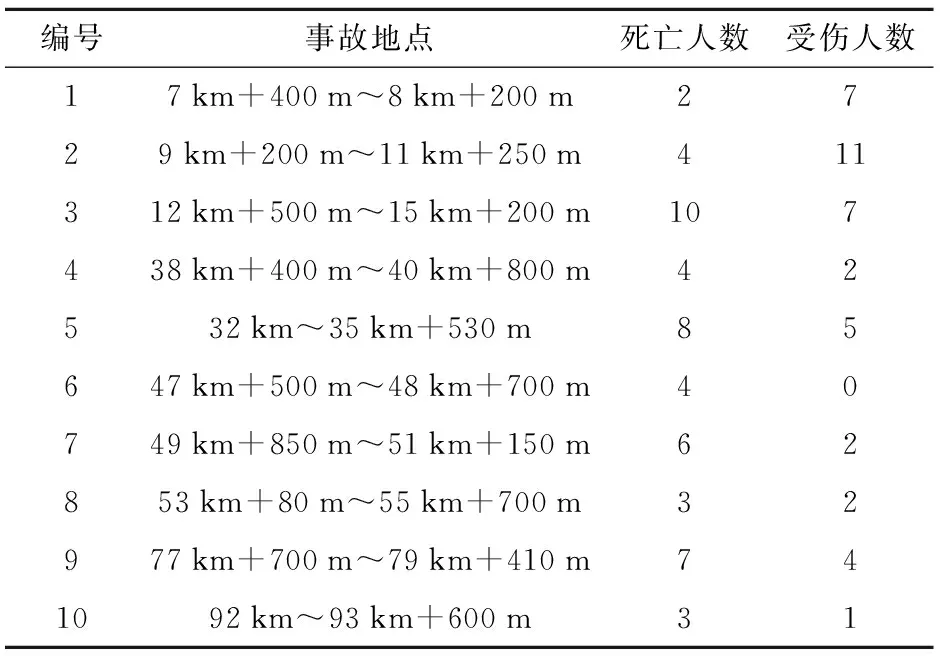
表2 该公路交通事故多发点段

依据交通事故多发点段的动态非定长划分技术路线，现将鉴别出的交通事故多发点段进行进一步精确其长度，剔除中间的安全路段。得到最终更加精确的交通事故多发点段数据，如表3所示。

表3 该公路交通事故多发点段精确表

5.2 事故多发点段等级评价

依据基于当量总事故率的事故多发点段等级评价方法，分别把各项数据代入到相应的公式中，最终得到：

一级交通事故多发点段有：38 km+400 m～40 km+800 m、47 km+500 m～48 km+700 m、53 km+80 m～55 km+700 m、92 km～93 km+600 m。

二级交通事故多发点段有：7 km+400 m～8 km+200 m、49 km+850 m～51 km+150 m、77 km+700 m～79 km+410 m。

三级交通事故多发点段有：9 km+200 m～11 km+250 m、12 km+500 m～15 km+200 m、32 km～35 km+530 m。

6 结论

本文在定义道路交通事故多发点段和充分考虑交通事故空间定位信息的基础上，基于聚类分析技术研究了一种道路交通事故多发点段的识别方法，同时设计一种事故多发点段空间范围的动态非定长划分方法，进而利用当量总事故率法将交通事故多发点段划分为3个风险等级，并给出了具体的划分标准。最后利用实际事故数据对模型进行了验证，证明所设计方法具有较高的可靠性。