基于小波神经网络模糊滑模控制的轮式移动机器人避障研究

王 韬

（长春职业技术学院工程技术分院，吉林长春130033）

近年来，机械、电子和计算机技术发展迅速，与此同时，人工智能技术发展也得到提升，从而诞生了机器人。机器人涉及机械、电子及人工智能等多种学科，目前的机器人不仅仅是替代人类劳动进行生产，也正在向人类学习思考方向发展。迄今为止，机器人在各个行业都得到了广泛应用，包括工业、农业、海洋、太空及医疗等领域[1-2]。轮式移动机器人是机器人研究发展的重要组成部分，它在移动过程中，能够检测到周围环境信息而做出避障运动，从而完成复杂任务。因此，研究轮式移动机器人避障问题，对于促进机器人学科领域的发展具有重要的意义。

当前，许多研究者从多种角度对轮式移动机器人避障方法展开了研究。例如：文献[3-4]研究了轮式移动机器人模糊控制方法，给出了三轮移动机器人运动学模型，设计了避障系统控制框图，根据模糊规则设计了模糊规划控制器，通过实验观察移动机器人避障效果，解决了轮式移动机器人避障任务。文献[5-6]研究了轮式移动机器人避障滑模控制方法，针对机器人运动存在未知扰动问题，设计了滑模控制器，采用李雅普诺夫函数对机器人运动的稳定性进行证明，通过仿真和实验验证滑模控制避障效果，解决了机器人视觉定位数据的丢失问题。文献[7-8]研究了移动机器人避障神经网络控制方法，采用权值调节收敛速度和学习效率，给出了BP神经网络避障控制模型，通过仿真验证BP神经网络避障控制效果，提高了机器人对障碍物的识别率。但是，以往研究的轮式移动机器人在中速和高速移动时，容易发生急转弯现象，导致轮式移动机器人发生侧翻，从而造成不必要的损失。对此，创建轮式移动机器人二维模型，根据拉格朗日定理推导出机器人动力学方程式。引用滑模控制器，采用小波神经网络和模糊规则对滑模控制器进行改进，设计了轮式移动机器人小波神经网络模糊滑模控制器。采用Matlab软件对轮式移动机器人避障效果进行仿真验证，并与滑模控制避障效果进行对比，为深入研究轮式移动机器人避障方法提供参考价值。

1 轮式移动机器人

本文在平面直角坐标系中建立轮式移动机器人运动轨迹简图，如图1所示。

图1 轮式移动机器人Fig.1 Wheeled mobile robot

图1中：O点为终点位置；M点为起始位置；v为机器人移动速度；ω为机器人旋转角速度；r为机器人运动距离；φ为机器人航向角偏差。

根据拉格朗日定理，可以推导出轮式移动机器人动力学方程式[9]为

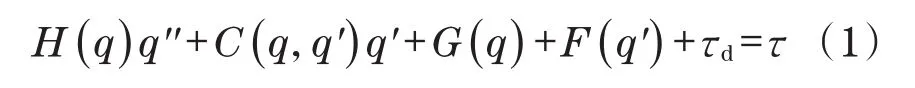
式中：H（q）为机器人惯性力矩；C（q，q'）为科氏力矩；G（q）为重力矩矢量；F（q'）为摩擦力矩矢量；τ为驱动力矩矢量；τd为外部干扰波形。

轮式移动机器人实际运动速度方程式[10]为

式中：（x，y，θ）为机器人实际位姿。

在直角坐标系中，非完整移动机器人跟踪误差变换方程式为

式中：（xr，yr，θr）为机器人期望位姿。

对式（2）求导后，可以推导出机器人跟踪误差方程式为

2 控制器设计

2.1 滑模控制

在有障碍物的环境中，轮式移动机器人跟踪目标就是使实际位姿与期望位姿吻合。定义的跟踪误差为qe=q-qr，其中，qe=[xe，ye，θe]，设计的滑模面[11]为

式中：s=[s1，s2，s3]T；Λ=diag（r1，r2，r3）为正对角矩阵，ri为滑模面斜率且ri＞0。

滑模控制器设计[11]为

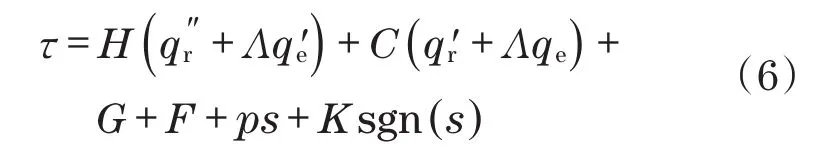
式中：p=diag（p1，p2，p3）为正对角矩阵，pi＞0；K=diag（k1，k2，k3）为正对角矩阵，ki＞0。

2.2 小波神经网络

小波神经网络是新的前馈神经网络模型，主要由小波变换理论和人工神经网络两个部分组成。小波函数由神经网络激励函数转换生成，具有很强的逼近和自适应学习能力。

输入变量为X=[x1，x2，…，xn]T，隐含层基向量为φ=[φ1，φ2，…，φm]T，激励函数采用小波函数[12]，即

式中：aj=[a1，a2，…，am]为神经网络节点伸缩参数；bj=[b1，b2，…，bm]为神经网络节点平移参数；ωj=[ω1，ω2，…，ωm]为神经网络权值矩阵。

小波神经网络第s个样本第k个神经元输出量为

为了对参数进行训练，采用小波神经网络误差函数进行评价，其表达式为

式中：E为误差；S为样本对数；L为网络输出节点数量为期望输出量。

神经网络参数采用梯度下降法进行训练，其表达式为

2.3 小波神经网络模糊滑模控制

令滑模控制器函数为

式中：x为输入变量。

采用小波神经网络对滑模控制器函数进行逼近，神经网络输入为

根据小波神经网络逼近定理，小波神经网络期望输出函数为

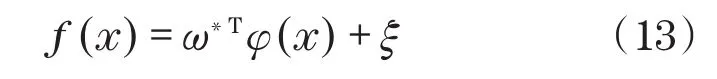
式中：φ（x）=[φ1，φ2，…，φn]T为小波输出函数；ω*为神经网络权值矩阵；ξ=[ξ1，ξ2，…，ξn]T为神经网络逼近误差。

小波神经网络实际输出函数为

取Δω=ω*-ω*a为逼近权值，Δω为权值误差，f（ax）为（fx）的网络逼近值。

机器人当前移动点到滑模面的距离公式为

通过di对滑模控制切换增益系数ki进行调整。模糊控制输入输出规则定义如下：若di为NBB，则ki为PBB；若di为NB，则ki为PB；若di为NM，则ki为 PM；若di为 NS，则ki为 PS；若di为NSS，则ki为PSS；若di为 Z，则ki为 Z；若di为 PSS，则ki为 PSS；若di为PS，则ki为PS；若di为PM，则ki为PM；若di为PB，则ki为PB；若di为PBB，则ki为PBB。

在上述模糊规则中，NB为负大，NBB为负大大，NS为负小，NSS为负小小，NM为负中，Z为零，PS为正小，PSS为正小小，PM为正中，PB为正大，PBB为正大大。

因此，小波神经网络模糊控制器设计为

2.4 稳定性分析

取

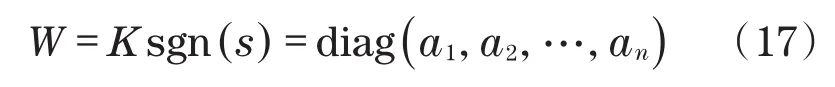
根据式（1）、式（5）和式（11）可得

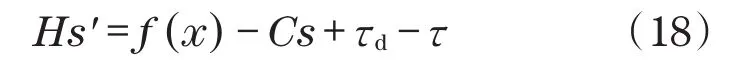
根据式（13）、式（16）和式（17）可得

根据模糊系统逼近定理，可以得到

控制系统自适应定律为

根据李雅普诺夫函数[13]可得

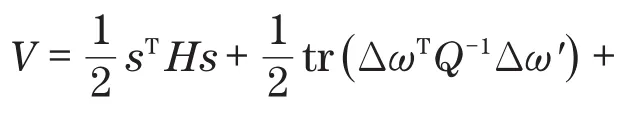
对式（17）求导变换后可得

假设正实数满足下列关系：

若0＜ρi＜1，则可以推导出

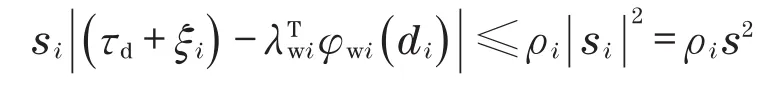
因此

式中：ρ=diag（ρ1，ρ2，···，ρn）。

取pi＞ρi，则可以推导出

根据李雅普诺夫判别定律可知，控制系统全局是稳定的。

3 仿真及分析

为了对比移动机器人在不同控制方法下避障效果，采用Matlab软件对移动机器人运动路径进行仿真。机器人参数设置如下：K=diag（0.4，0.4，0.4），Q=diag（30，30，30），P=diag（60，60，60），Λ=diag（6，6，6），初始位姿为q=（0，0，0）。假设机器人移动速度分别为低速（40 km/h）、中速（80 km/h）和高速（120 km/h），则移动机器人避障碍效果分别如图2～图4所示。

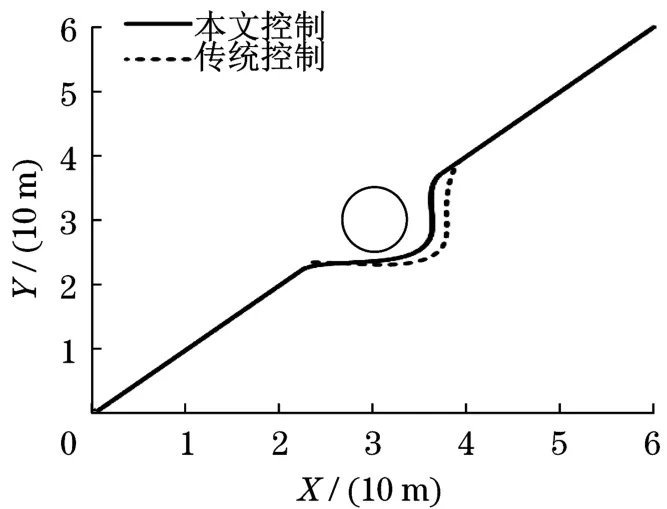
图2 低速避障效果Fig.2 Obstacle avoidance effect at low speed

根据图3可知：在低速行驶时，采用滑模控制和小波神经网络模糊滑模控制方法，移动机器人基本上在同一位置做出反应，能够较好地避开障碍物。根据图4可知：在中速和高速行驶时，采用滑模控制方法，移动机器人离障碍物较近时才开始做出反应，反应速度较慢，而采用小波神经网络模糊滑模控制，机器人离障碍物较远时就开始做出反应，反应速度较快。因此，移动机器人采用小波神经网络模糊滑模控制方法，能够提前预测到障碍物，避免移动机器人发生急转弯现象，从而避免机器人发生侧翻现象。

图3 中速避障效果Fig.3 Obstacle avoidance effect at medium speed

图4 高速避障效果Fig.4 Obstacle avoidance effect at high speed

4 结论

本文研究了移动机器人避障问题，采用小波神经网络模糊滑模控制方法，并对避障效果进行仿真验证，主要结论如下：①小波神经网络模糊滑模控制方法，结合了小波神经网络和模糊滑模控制的各自优点，具有在线自适应调节功能；②移动机器人采用小波神经网络模糊滑模控制方法，遇到障碍物时，能够提前预测到，迅速做出反应，有效地避开障碍物，避免急转弯导致机器人发生侧翻现象；③采用Matlab软件对移动机器人在有障碍物环境中进行仿真，模拟移动机器人在复杂环境中工作效果，进一步验证小波神经网络模糊滑模控制的先进性，为深入研究移动机器人控制方法提供理论依据。