基于人工鱼群算法优化的车辆防滑PID神经网络控制研究

麦 鹏

（西安汽车职业大学汽车工程学院，陕西西安710600）

随着社会的发展，汽车保有量也在逐步上升，同时车辆行驶的安全性也越来越受到高度关注。车辆在复杂路况行驶时，在转弯时容易发生侧滑甚至发生漂移现象，导致车辆发生交通事故[1-2]。在车辆安全性控制方面，路面滑转率参数识别变得非常重要。车辆侧滑控制系统就是要使控制的车辆滑转率在最优附近，保持车辆尽可能利用路面附着系数。复杂路况不同路段，最优滑转率也各不相同。车辆控制系统能够对路面滑转率进行预估，做出判断后迅速调整控制参数，从而使车辆稳定、安全行驶。因此，研究车辆驱动防滑控制系统，对于提高车辆行驶的安全性变得非常关键。

当前，车辆防滑控制技术吸引了很多研究者的关注，从而产生许多理论方法。例如：文献[3-4]研究了四轮车辆独立驱动防滑模糊控制方法，给出了单轮车辆动力学模型，设计了模糊控制器，建立整车模糊控制算法仿真模型，缩短了车辆的滑转调节时间。文献[5-6]研究了客车电驱动非线性模型预测控制方法，建立整车动力学模型，设计非线性模型最优滑转率控制目标函数，采用仿真验证不同路况滑转率跟踪效果，增强了车辆驱动能力和稳定性。文献[7]研究了拖拉机驱动改进PID控制方法，建立车轮滑转率方程式，引用PID控制方法，采用改进粒子群算法优化PID控制参数，通过不同路况对拖拉机滑转率进行仿真，有效地抑制了滑转率突变现象。以往研究的车辆防滑控制系统容易受到路面激励波形的干扰，对此，引用多神经网络结构，设计了PID神经网络控制系统，采用人工鱼群算法优化PID神经网络控制方法。采用数学软件Matlab对车辆防滑控制系统跟踪效果进行仿真验证，并且与传统PID控制效果进行比较，为深入研究车辆行驶的稳定性和安全性提供理论依据。

1 车辆驱动模型

采用简化模型对车辆驱动进行分析，如图1所示。通过对车辆进行受力分析，可以推导出车辆动力学方程式[8]为

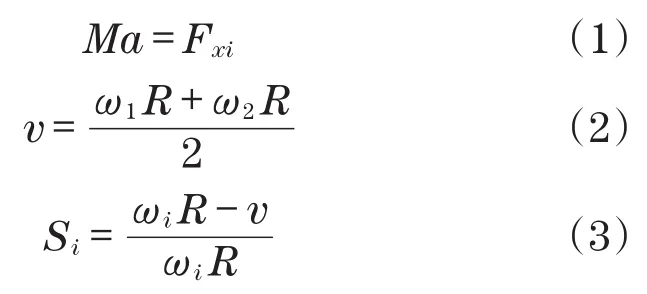
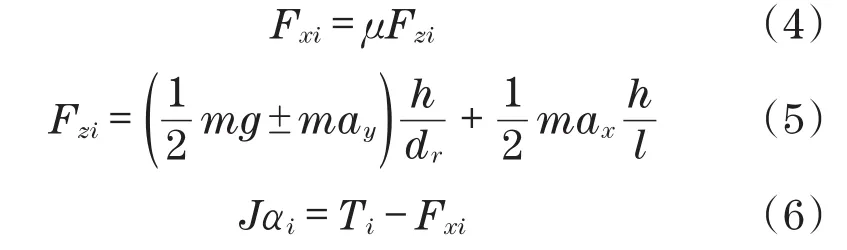
式中：M为车辆质量；Fxi为后轮驱动力；J为车轮转动惯量；αi为后轮角加速度；Ti为后轮力矩；v为车辆运动速度；ω1，ω2为前轮角速度；ωi为后轮角速度；Si为后轮滑转率；μ为路面附着系数；Fzi为后轮承载力；ay为车辆横向加速度；h为车辆质心高度；dr为后轮轮距；ax为车辆纵向加速度；l为前轮和后轮轴距。

图1 车辆驱动模型简图Fig.1 Vehicle driving model diagram

车辆在不同路面行驶，轮胎与路面附着系数也不相同，轮胎滑移率与附着系数的关系式[9]为

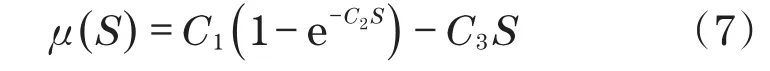
式中：C1，C2，C3为拟合系数；S为轮胎滑移率；μ为附着系数。

最优滑移率和最大附着系数计算公式为

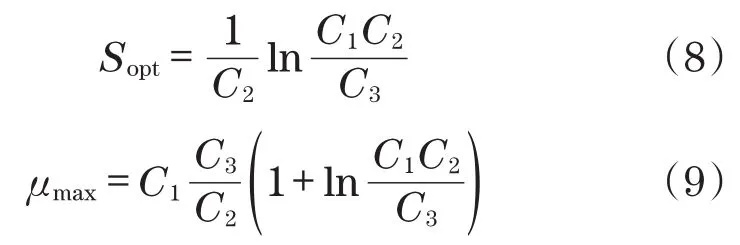
2 PID神经网络控制

2.1 PID神经网络控制结构

假设控制对象包括n输入和n输出的多变量参数，则PID神经网络控制器为2n×3n×n的三层前向网络结构。PID神经网络包含输入层、隐含层和输出层[10]。多输入多输出的PID神经网络的控制系统结构如图2所示。图中：r1，r2，r3为控制系统理论输入值；u1，u2，u3为PID神经网络输出值；y1，y2，y3为控制系统输出值。

2.2 PID神经网络控制算法

PID神经网络各层控制算法计算公式如下：

输入层：主要包括2n个神经元，其输入、输出函数关系式[11]为

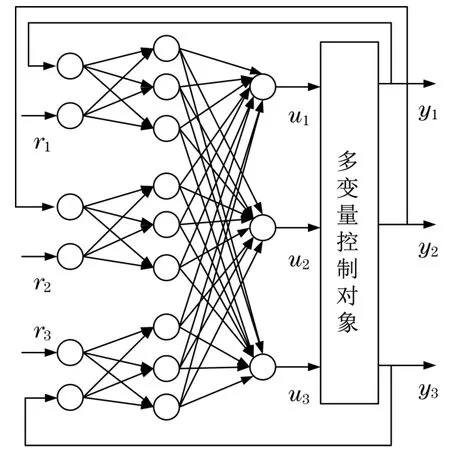
图2 多输入多输出PID神经网络控制结构Fig.2 PID neural network control structure with multi input and multi output

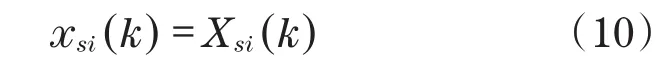
式中：Xsi为输入层的输入值；xsi为输入层的输出值；k为采样时刻；s为子网序号；i为输入层序号。

隐含层：主要包括比例、积分和微分神经元各n个。三种神经元输入方式是相同的，其计算公式[11]为

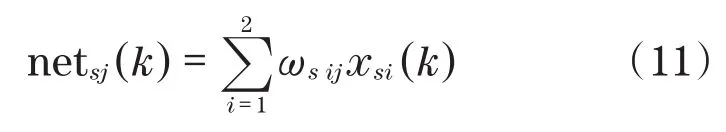
在输出方式上，三种神经元各不相同，其中，比例神经元输出方式为

积分神经元输出方式为

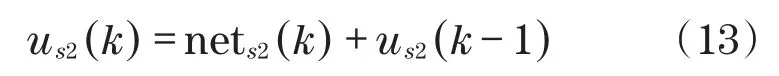
微分神经元输出方式为

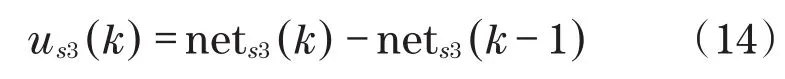
式中：j为隐含层序号；wsij为输入层与输出层调整权值；xsi为神经网络输出值。

输出层：主要包含n个神经元，输出层输入值计算公式为

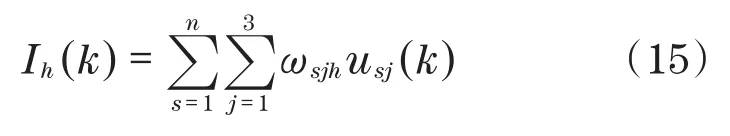
输出层输出计算公式为

式中：h为输出层序号；usj为隐含层输出值；ωsjh为隐含层与输出层连接权值。

PID神经网络学习目标函数为

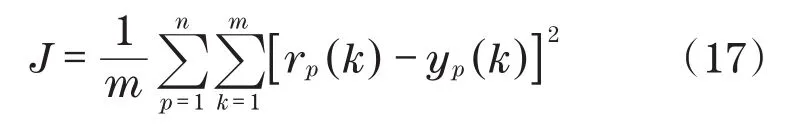
式中：m为采样点数；n为控制变量个数；rp为系统输入值；yp为系统输出值。

3 改进PID神经网络控制

3.1 人工鱼群算法

人工鱼群算法是通过模拟鱼群的觅食、聚群、追尾行为，从而达到全局优化的目的。假设人工鱼群当前状态为Xi，随机生成另外一种状态为XjXi=[xid]，Yi=f（Xi），其中f（）为目标函数。人工鱼个体之间的距离为dij=Xi-Xj，其拥挤度因子为δ，移动步长为step，视野范围为visual。人工鱼群算法具有以下几种行为：

（1）觅食行为。人工鱼群算法当前状态为Xi，在感知范围内，随机生成另外一个状态Xj。若Yi＜Yj，则向前移动一步，即Xi/n；否则，重新生成随机状态Xj，多次尝试后仍然不满足条件，则随机移动一步。其表达式为

式中：step为人工鱼移动的步长；R（）函数为区间[0，1]随机数。

（2）群聚行为。人工鱼群在可视范围内中心位置状态为Xc，若Yc/nf＞δYi（nf为同伴数目），表明同伴中心食物较多且周围不太拥挤；否则，执行觅食行为。其表达式为

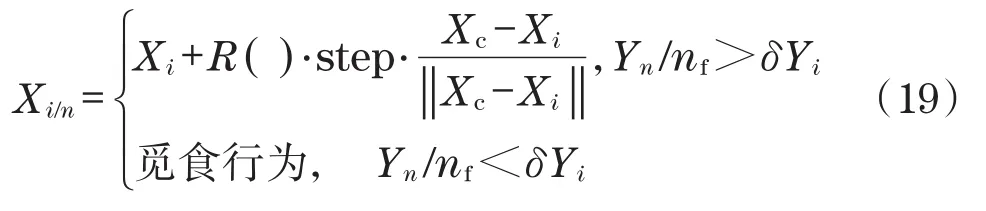
（3）追尾行为。人工鱼群在可视范围内搜索到的食物浓度最大状态为Xm，若Ym/nf＞δYi，表明Xm状态食物浓度较高且周围不太拥挤，则Xm向前移动一步；否则，执行觅食行为。其表达式[12为

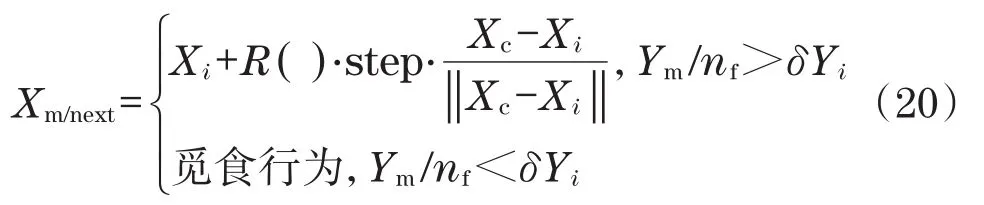
3.2 人工鱼群算法优化步骤

步骤1定义参数变量：设置鱼群数量为N，最大迭代次数为Tmax，拥挤度因子为δ，移动步长为step，视野范围为visual，最大试探次数为try。

步骤2计算初始鱼群自身状态变量，选择最优值赋给公告板。

步骤3每条个体鱼通过觅食、追尾和聚群行为后，对比行为前后状态向量，选取较优行为执行，通过神经网络学习目标函数评价个体的状态向量。

步骤4对比适应度值，选择个体鱼状态最优值与公告板状态进行对比，若个体鱼优于公告板状态，更新公告板状态，若公告板优于个体鱼状态，则保持不变。

步骤5判断迭代次数，若达到最大迭代次数，则输出最优值，否则，跳到步骤3。

步骤6将最优值输入到PID神经网络控制器，用于控制车辆滑移。

4 仿真及分析

为了验证人工鱼群算法优化PID神经网络控制效果，采用Matlab软件对车辆滑移跟踪进行仿真。仿真参数设置如下：人工鱼群数量N=50，最大迭代次数Tmax=200，拥挤度因子δ=0.625，移动步长step=0.3，视野范围为visual=0.5，最大试探次数try=50，输入层到隐含层学习速率ηsij=0.001，隐含层到输出层学习速率ηsjh=0.006。假设车辆以20 km/h行驶路面附着系数分别为0.6，0.2和0.4，车辆驱动力矩分别为600，200和400 N·m。采用PID控制方法，车辆滑移率和驱动力矩仿真结果分别如图3和图4所示；采用人工鱼群算法优化PID神经网络控制方法，车辆滑移率和驱动力矩仿真结果分别如图5和图6所示。

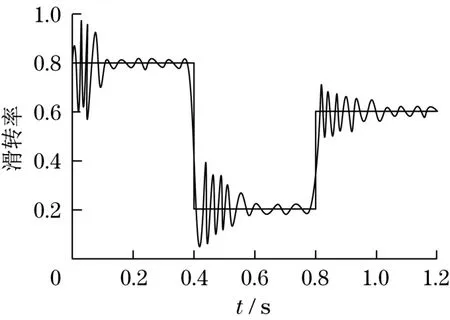
图3 滑转率PID控制Fig.3 Slip rate by PID control

图4 驱动力矩PID控制Fig.4 Driving torque by PID control

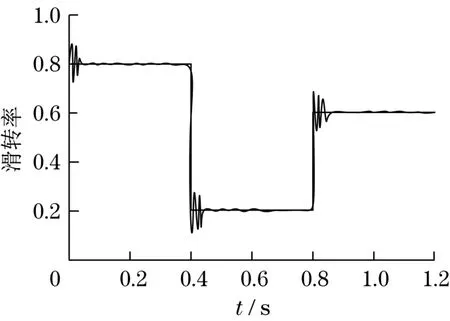
图5 滑转率改进PID控制Fig.5 Slip rate by PID control

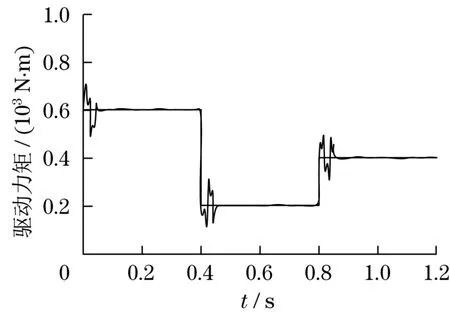
图6 驱动力矩改进PID控制Fig.6 Driving torque with improved PID control

由图3和图4可知：采用传统PID控制方法，车辆实际滑转率和驱动力矩与理论值偏离较大，滑转率和驱动力矩波动幅度较大。由图5和图6可知：采用人工鱼群算法优化PID神经网络控制方法，车辆实际滑转率和驱动力矩与理论值偏离较小，滑转率和驱动力矩波动幅度较小。车辆在复杂路面环境中行驶，容易受到多种因素的干扰，传统PID控制方法反应速度慢。而人工鱼群算法优化PID神经网络控制方法，反应速度快，能够快速地调节PID控制参数，使控制系统快速地适应复杂路况。因此，采用人工鱼群算法优化PID神经网络控制方法，控制系统运行相对稳定，从而防止车辆发生侧滑现象。

5 结论

针对车辆在复杂路面行驶容易发生侧滑问题，采用改进PID控制方法，并对跟踪效果进行仿真实验，主要结论如下：①采用改进PID控制方法，能够抑制复杂路况波形的干扰，在线输出PID控制最优参数；②车辆行驶在复杂路况上，传统PID控制滑转率产生的偏差较大，车辆加速时间较长，而采用改进PID控制滑转率产生的偏差较小，车辆加速时间较短；③与传统PID控制相比，改进PID控制超调量较小，车辆驱动力矩跟踪效果较好，对车辆产生的振动幅度较小，车辆行驶较为稳定。