基于视频图像处理的滑动摩擦系数测量

段 茜，廖 凯，于锐锐，蒋 荣，曾 斌

(西南石油大学 理学院，四川 成都 610500)

2个物体的干燥接触表面之间的干摩擦力，在实际工程中广泛存在. 滑动摩擦系数作为重要的技术参量，常用于研究由摩擦引起的非线性动力学现象[1-3]. 同时，滑动摩擦系数的精确测定，对于选择合适的工作参量以完成实际工程中的预定要求也具有重要的指导意义[4-6].

目前对滑动摩擦系数的测量方法主要分为两大类，一类是机械传动式测量方法[7]，另一类是采用力传感器，通过测量摩擦过程中的正压力和摩擦力来求得摩擦系数[8-10]，但二者都存在着实验精度不好控制，测量结果不够精确的问题. 本文提出了基于视频图像处理技术[11]的非接触式测量方法，通过测量在小阻尼情况下双弹簧振子的振动曲线计算滑动摩擦系数，并以钢与木材之间的滑动摩擦系数为例进行了计算，将计算结果与文献[12]中的参考值对比，验证了结果的合理性. 该方法仅从一次实验中就可得到较多与滑动摩擦系数有关的数据.

1 实验原理

如图1所示，2根轻弹簧两端固定，中间系一滑块，构成了水平双弹簧振子系统，让滑块做往返振动，考虑滑块与接触表面之间的干摩擦阻力f，假设f的大小不变，其方向始终与运动方向相反，那么滑块的振动为阻尼振动，其位移逐步减小为零. 设滑块的质量为m0，弹簧的质量分别为m1和m2，劲度系数分别为k1和k2，滑块与接触表面之间的滑动摩擦系数为μ.

图1 水平双弹簧振子示意图

当滑块处于平衡位置O时，弹簧的伸长量分别为x1和x2，以平衡位置O为原点，水平向右为x轴正向，建立一维坐标系，则

-k1x1+k2x2=0.

(1)

当滑块距离平衡点为x且自右向左运动时，滑块运动的微分方程为

(2)

其中，

(3)

为振动系统的有效质量[13]. 考虑式(1)，则式(2)化简为

(4)

同理，当滑块自左向右运动时，滑块运动的微分方程为

(5)

令

(6)

(7)

则解得式(4)和式(5)的通解分别为

x=Acos (ωt+φ)+C,

(8)

x=Acos (ωt+φ)-C,

(9)

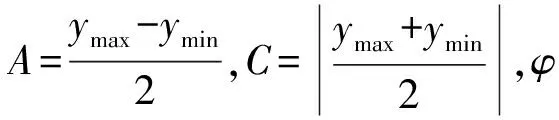
尽管阻尼振动不是严格的周期运动，但如果仍把滑块往复运动1次所用的时间称为周期，振动仍具有等时性. 因为在振动的各个阶段角频率ω都相同，周期T表示为

(10)

2 实验方法

2.1 双弹簧振子振动视频图像的获取与预处理

图2 弹簧振子的原始图片

图3 预处理后的滑块图片

2.2 图像单个像素大小的标定与滑块平衡位置的确定

摄像机参量的标定是计算滑块振动参量的前提，其标定结果的精度将直接影响各个振动参量结果的准确性. 考虑到需要求解的物理量是滑块的位移，而滑块的实际空间点坐标可以不必计算. 因此本文采用了简单易行的标定方法，即仅标定图像单个像素的大小，从而避免了复杂求解摄像机参量的过程，且标定精度完全满足实验需求. 标定方法如下：滑块为精密加工的圆柱形不锈钢钩码，因此可将其过圆心的横截面积作为参照物对图像像素大小进行标定，逐帧计算视频1中预处理后滑块的面积，并取平均作为滑块的图像面积，得到结果为2 134 pixel. 由于滑块的图像面积是对大量图像(大于100帧)取平均的结果，因此其测量带来的偶然误差可以忽略不计. 已知滑块的实际横截面积为

S=2rh=350.00 mm2,

(11)

计算得到图像单个像素的面积为0.16 mm2，单个像素的边长为0.40 mm，并将此作为标定系数应用在振动参量的计算中. 注意到视频每帧图像分割出来的滑块目标形状并不完全相同，因此提取滑块的质心坐标作为滑块的准确位置. 将视频1中每帧滑块的质心坐标求平均，得到滑块的平衡位置O点的像素坐标为(320.95，256.75).

2.3 滑块阻尼振动曲线的绘制以及滑动摩擦系数计算

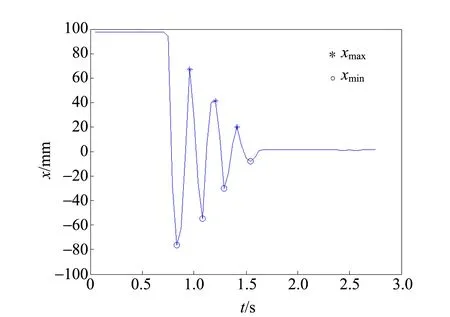
图4 视频2中滑块的位移-时间曲线

将视频2中每帧滑块的质心像素坐标求出，令其横坐标与平衡位置O点的横坐标相减，再乘以单个像素长度的标定系数0.40 mm，便可得到滑块的实际位移量. 绘制每帧滑块的位移，并将帧数换算成时间，得到滑块的位移-时间曲线，如图4所示. 找出滑块位移-时间曲线的位移极大值和极小值坐标点，列于表1中. 计算两相邻位移极大值与极小值之间的时间间隔，并取平均值再乘以2作为滑块的振动周期，结果为0.236 1 s. 滑块振动的理论周期由式(10)计算为0.235 0 s，二者相对偏差仅为0.47%，证明了滑块阻尼振动曲线的准确性. 将滑块位移极大值与其前一位移极小值求平均，即可得到动平衡位置-C，将位移极大值与其后一位移极小值求平均，即可得到动平衡位置C，结果列于表2中.

表1 滑块的位移-时间曲线参量

表2 滑块的动平衡位置

将表2中所有动平衡位置取绝对值再求平均，结果为5.729 9 mm，代入式(7)即可求到滑动摩擦系数μ为

(12)

将该结果与文献[3]中软木与钢的干摩擦因数0.30～0.50对比，结果在正常范围之内，说明了该方法的正确性. 对同一段松木板反复测试，计算所得的滑动摩擦系数结果略有波动，相对偏差不超过4.8%，这也充分说明了该方法的精确性.

3 结束语

基于计算机视频图像处理技术，提出了非接触式的测量滑动摩擦系数的方法，该方法原理简单、操作简便且计算精度高，可以测量常用材料之间的滑动摩擦系数. 但值得注意的是，在测量不同材料之间的滑动摩擦系数时，要选择合适的滑块质量及弹簧劲度系数，使滑块作小阻尼振动，不要出现临界阻尼和过阻尼的情形.