轻重物体系绕杆运动的循环摆现象研究

曾溢嘉，王晓杰，李文华，陈宗强

(南开大学 物理科学学院，天津 300071)

第32届国际青年物理学家锦标赛(IYPT)的第14题[1]为： Connect two loads, one heavy and one light, with a string over a horizontal rod and lift up the heavy load by pulling down the light one. Release the light load and it will sweep around the rod, keeping the heavy load from falling to the ground. Investigate this phenomenon. 本题要求对轻物如何通过扫动阻碍重物落向地面的过程进行研究. 本文结合力学分析与模拟，研究了轻物的扫动轨迹与重物的下落过程.

1 理论分析

1.1 重物下落过程

循环摆系统主要由一轻一重两物体(质量分别为m和M)、水平杆(半径R)和轻质绳构成. 将轻重两物体简化为质点，将绳简化为不会伸长、无质量的理想绳，并忽略空气阻力[2-3]. 两物体质量比定义为：k=m/M. 如图1所示，其中，A表示轻物体端绳与杆的切点，r表示轻物体m到切点A的距离，θ表示轻物体端绳与轴夹角，R表示杆的半径，z表示重物体M到重物体端绳与杆的切点的距离，T和T′分别表示轻重物体端绳上的拉力. 以杆中心O为原点建立直角坐标系xOy(简称坐标O系),再以轻物体端绳与杆的切点A为原点建立直角坐标系x′Ay′(简称坐标A系).

图1 循环摆结构示意图

先分析A点相对O点的运动，根据图2(a)所示的A点运动示意图，可以算出A点相对于O点的运动速度为

(1)

因此，A点相对O点的径向和切向加速度分别为

ar=Rω2，

(2)

(3)

其方向如图2(b)所示.

对轻物体进行受力分析，如图3所示，其中mar，maτ表示由A点相对于O点运动引起的惯性力. 根据牛顿运动定律，轻物体在坐标A系水平方向与竖直方向的运动方程分别为[4]

(4)

(5)

其中，θ满足：

(6)

(7)

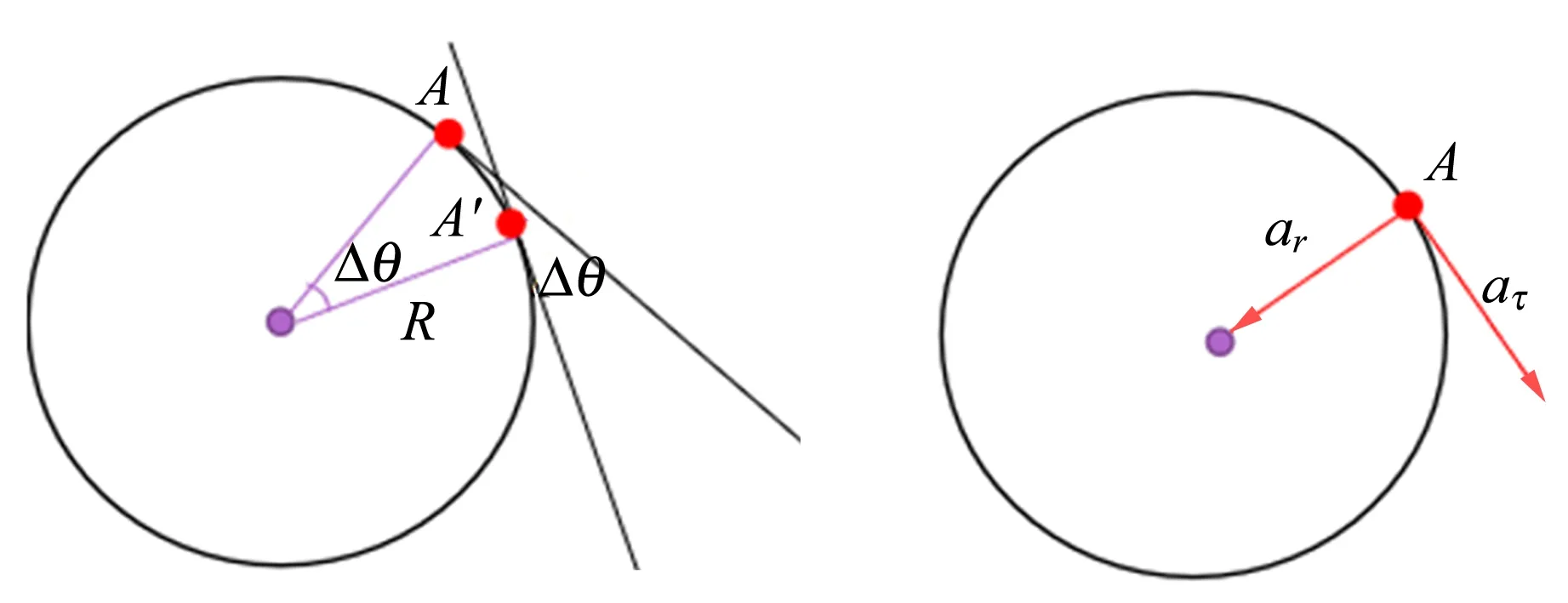
(a)A点运动 (b)A点对地加速度 图2 A点运动及对地加速度示意图

图3 A系中轻物体受力分析示意图

现在需要在坐标O系中求得T的表达式. 如图1所示，在坐标O系中，根据牛顿运动定律，在沿绳方向上有：

ma=T-mgsinθ,

(8)

加速度a可以由图1中几何关系求得：

(9)

其中，r0和θ0分别表示t=0时刻r和θ初始值，即轻物体端原始绳长和释放时轻物体端绳与x′轴夹角.

将式(9)代入式(8)中，得到T的表达式为

(10)

对于重物体端受力进行分析，其运动方程为

(11)

根据文献[5-6]，取杆上线元进行受力分析再积分，对轻绳两端的张力有：

(12)

其中，μ为绳与杆之间的摩擦系数. 分别令r0和z0为轻物体端和重物体端原始绳长，在总绳长不变的前提下，任意时刻的绳长满足：

(13)

联立式(11)～(13)，可以得到重物体在竖直方向的运动方程为

(14)

综上，将式(6)，(7)，(10)和式(14)代入式(4)和式(5)中，得到在A系中轻物体m的运动微分方程. 利用O和A两系坐标的转换关系：

x=x′+Rsinθ，

(15)

y=y′+Rcosθ，

(16)

得到坐标O系(即地面系)中物体的运动方程.

1.2 重物体静止时

重物体静止时，轻物体的运动受到几何条件的约束. 在坐标A系中，轻物体m相对于A点的力矩为

(17)

此时，拉力T依然满足式(7)，只不过此时由重物体运动引起的加速度变为0，即

(18)

建立如图4所示的θ-r极坐标系，其中r表示轻物体m到切点A的距离，θ表示轻物体端绳与水平方向夹角，L表示轻物体到过A点竖直线的距离，R表示杆的半径. 物体所受几何约束可以表示为

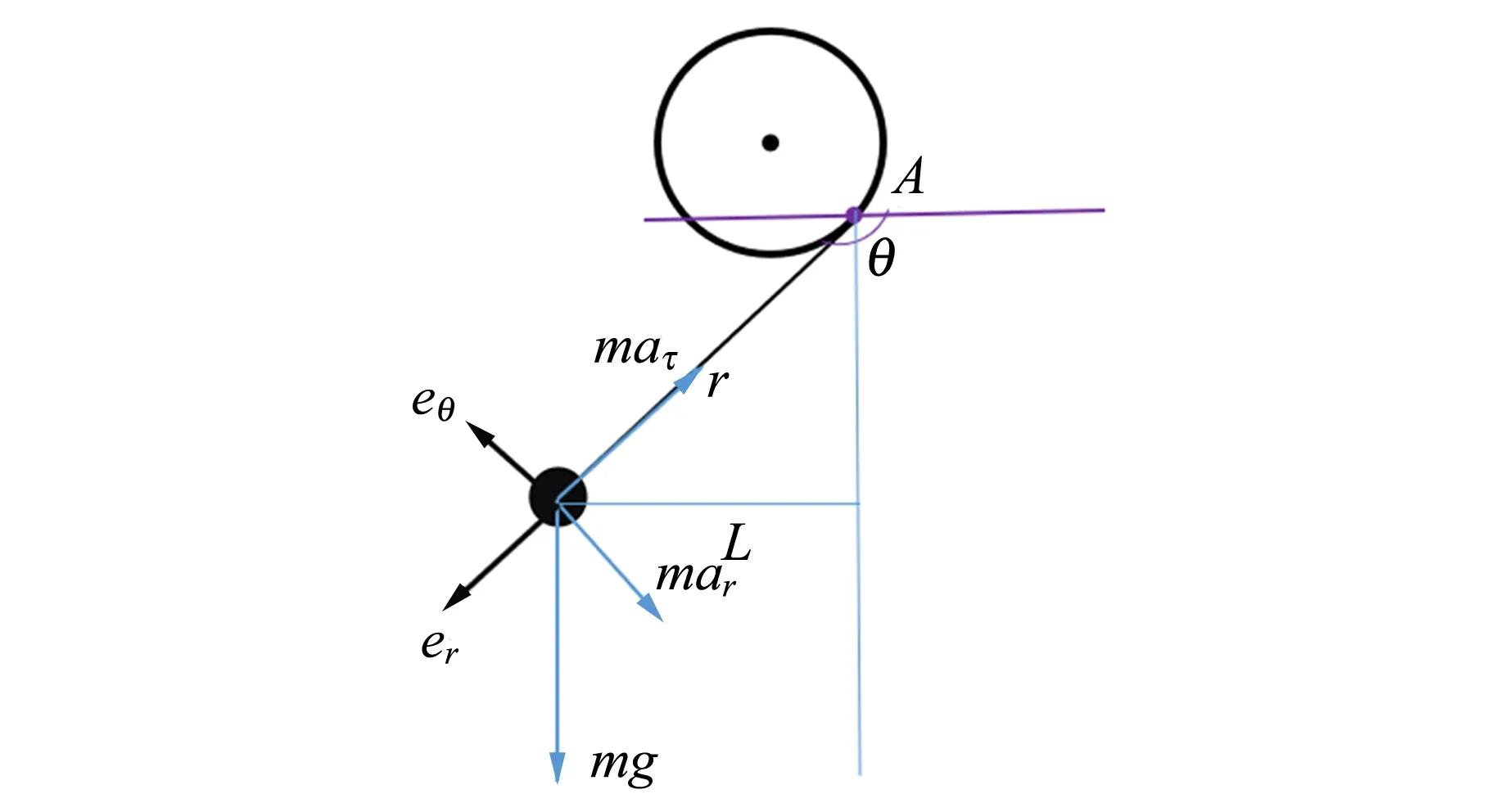
图4 坐标A系中轻物体受力分析示意图

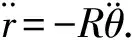
(19)

式(17)和式(19)联立，即是A系中轻物体运动的微分方程，再由O和A两系坐标的转换关系式(15)和式(16)，得到O系中物体的运动方程.

1.3 重物体运动与静止的临界条件

2 仿真模拟

2.1 轻重物体的质量比对循环摆运动的影响

固定β=90°，r0=0.628 m，μ=0.23，R=4.85 mm，逐渐增大轻重物质量比k，绘出轻物的运动轨迹. 图5为模拟结果中具有代表性的几例轨迹，分别对应了在不同初始条件下，循环摆现象中可能出现的不同情况：

1)当质量比k较小(0.10)时，重物体经过1次下落之后不再运动，直到轻物体端绳长减小到0. 图5(a)所示的运动轨迹是最典型的循环摆运动曲线.

2)当质量比k逐渐增大时(临界值～0.24)，重物体在整个过程中会出现2次下落，最终轻物体端绳长收缩到0，如图5(b)所示. 这是由于在运动过程中质量比k较大，导致轻物体速度较小，无法产生足够的拉力，从而引起重物体再次下落.

3)当质量比k增大到临界值时(0.34)，轻物体会在轻物体端绳长不为0时与杆发生碰撞，从而轻物体被杆弹回，同时，重物体直接落向地面. 图5(c)为轻物能否阻碍重物体落向地面的临界情况.

4)当质量比k大于临界值时，轻物体的速度将无法支持其继续向上运动，回荡下来，而重物体直接落向地面. 图5(d)所示的轨迹是无法阻碍重物体下落的最常见情况.

(a)k=0.10

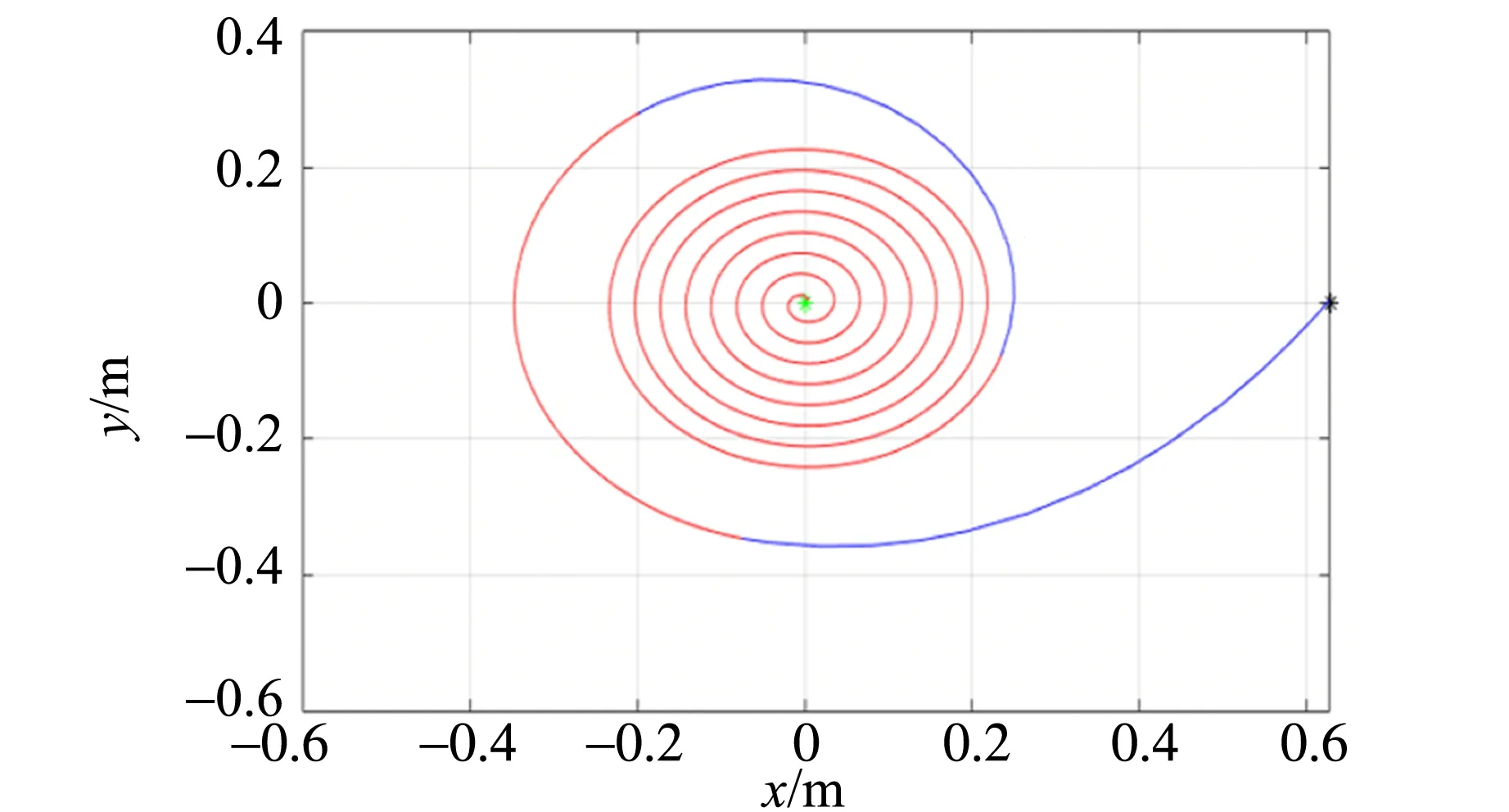
(b)k=0.25

(c)k=0.34

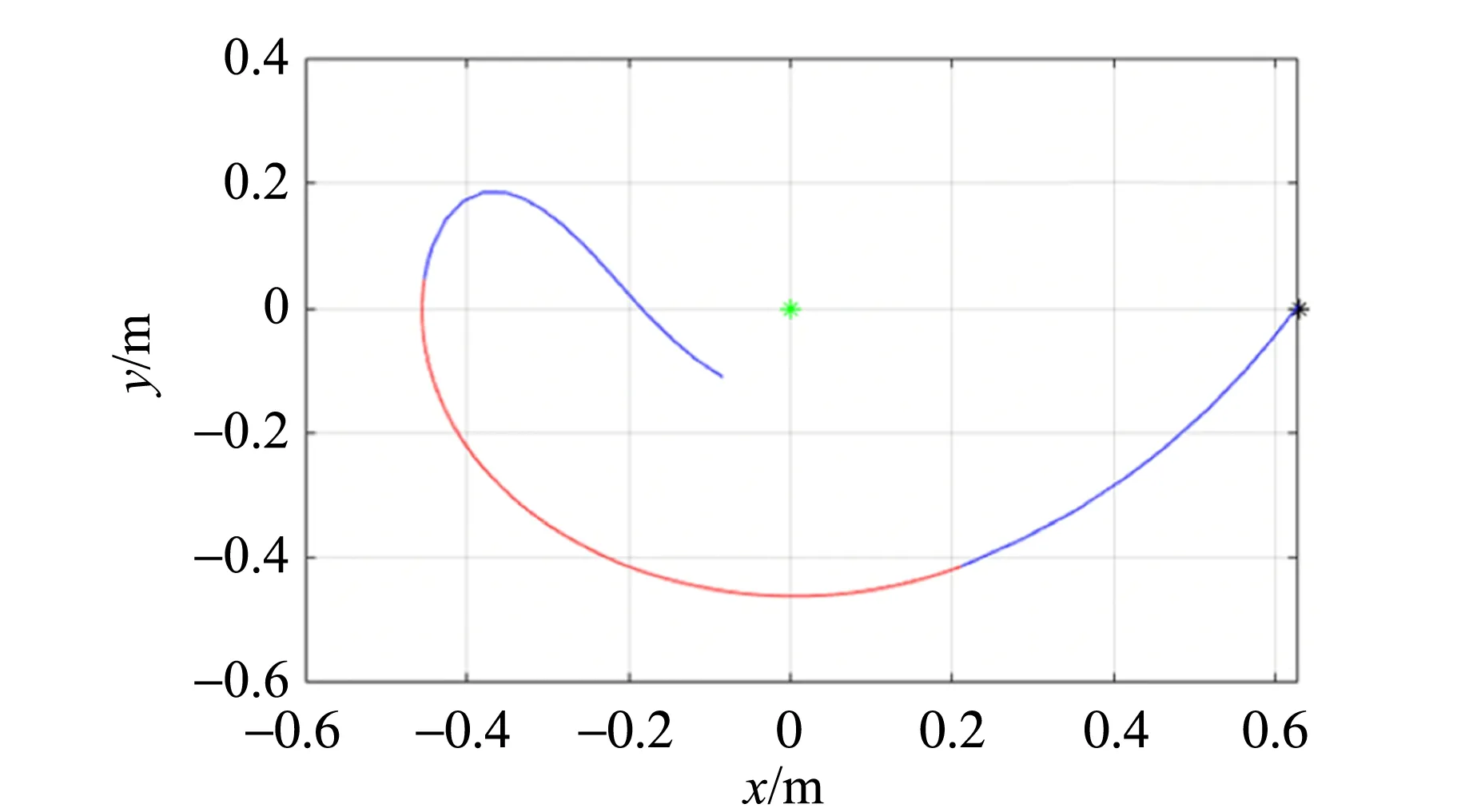
(d)k=0.50图5 不同质量比k时轻物体的运动轨迹(蓝色段表示重物体在下落，红色段表示重物体处于静止)

经大量数据模拟后，发现在质量比k小于临界值(一般在0.27～0.43，取决于其他初始条件)时，随着质量比k的增大，轻物体会越来越难以阻碍重物体的下落，并会出现多次下落. 在k值达到临界值以上之后，轻物体将不能完成绕杆扫动，也无法阻碍重物体下落至地面.

2.2 释放角度比对循环摆运动的影响

固定k=0.30，r0=0.628 m，μ=0.23，R=4.85 mm，改变β，模拟结果如图6所示.

1)当释放角度为90°时，轻物体可以完成绕杆扫动1周，最终阻碍重物体下落，如图6(a)所示.

(a)β=90°

(b)β=73°

(c)β=70°图6 不同轻物体释放角度下轻物体的运动轨迹(蓝色段表示重物体在下落，红色段表示重物体处于静止)

2)当释放角度为73°时，轻物体会在轻物体端绳长不为0时与杆发生碰撞，从而轻物体被弹回，重物体直接落向地面，如图6(b)所示.

3)当释放角度为70°时，轻物体的速度不支持轻物体绕杆1周，最终轻物体荡回，重物体落向地面，如图6(c)所示.

经过大量的数值模拟，发现释放角度越小，轻物体越难以阻碍重物体的下落. 当释放角度减小到临界值(一般在68°～90°，取决于其他初始条件，未考虑90°以上的情况)后，轻物体不能完成绕杆扫动，也无法阻碍重物体落向地面.

2.3 绳长对循环摆运动的影响

固定k=0.10,β=90°,μ=0.23,R=4.85 mm，改变初始绳长r0，轻物的运动轨迹结果如图7所示,可以看出绳长的改变并不会对轻物体曲线与重物体下落造成显著影响.

(a)r0=0.428 m

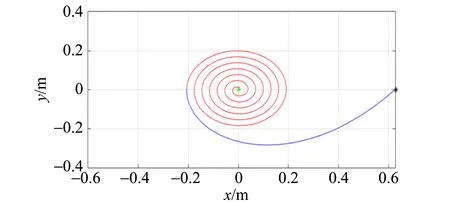
(b)r0=0.628 m图7 不同初始绳长下轻物体的运动轨迹(蓝色段表示重物体在下落，红色段表示重物体处于静止)

2.4 摩擦系数对循环摆运动的影响

取k=0.10,β=90°，r0=0.628 m，R=4.85 mm，改变摩擦系数μ，探究其对轻物体运动轨迹的影响.

不同摩擦系数μ下轻物体的运动轨迹如图8所示. 其中μ=0.23时用绿色和黑色曲线表示，其中绿色部分表示重物体在下落，黑色部分表示重物体处于静止；μ=0.53时用蓝色和红色曲线表示，其中蓝色部分表示重物体在下落，红色部分表示重物体处于静止. 从图8中可以发现，随着μ的增大，曲线向外扩张. 通过比较绿色与黑色曲线长度，发现在μ较大时，下落距离明显减小.

当μ=1.00，循环摆出现摆回现象. 轻物体运动轨迹如图9所示，即轻物体绕杆1周后速度不能支撑其做第2次绕杆，这是由于μ太大，重物体下落距离减小，轻物体速度过慢. 虽然轻物体无法再次完成绕杆运动，但并不妨碍其借助绳与杆之间的摩擦力阻碍重物体落向地面，这种情况下，仍然认为其完成了循环摆现象.

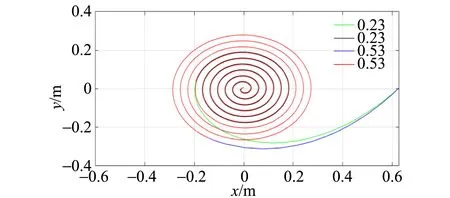
图8 不同摩擦系数μ下轻物体的运动轨迹

图9 μ=1.00时轻物的运动轨迹(蓝色部分表示重物体在下落，红色部分表示重物体处于静止)

2.5 杆半径对循环摆运动的影响

取k=0.10，β=90°,r0=0.628 m，μ=0.23，改变杆半径R，探究其对轻物体运动轨迹的影响.

图10为不同杆半径R下轻物体的运动轨迹，R=0.003 m时用绿色和黑色曲线表示，其中绿色部分表示重物体在下落，黑色部分表示重物体处于静止；R=0.005 m时用蓝色和红色曲线表示，其中蓝色部分表示重物体在下落，红色部分表示重物体处于静止. 从图10中可以发现，杆半径R较大时，重物体下落阶段轨迹并不会发生明显变化，这是由于这一阶段θ的变化往往不大导致的. 而对于θ明显变化的重物体静止阶段，R较大对应的运功轨迹处于内侧.

图10 不同杆半径R下轻物体的运动轨迹

3 实验研究

为了验证数值模拟的结果，实验使用高速摄像机记录循环摆轻物的运动过程，再用Tracker软件进行打点分析. 实验中所使用的摄像机为高速相机FDR-AX700，拍摄帧率为120帧. Tracker软件版本为5.1.0. 绳长、角度用Tracker定标测量的方法(长度定标尺精度为1 mm，角度定标尺精度为0.1°)，杆直径用游标卡尺测量(精度0.02 mm)，轻重物体的质量用电子称测量(精度0.01 g)，实验装置如图11所示. 实验得到细绳和杆的摩擦系数μ=0.230和杆半径R=4.85 mm.

图11 实验装置图

3.1 轻物体的运动轨迹

首先，记录能阻碍重物体落向地面时不同实验条件下轻物体的运动轨迹. 实验结果如图12所示，黑色曲线为实验轨迹，蓝色曲线和红色曲线表示理论运动轨迹，蓝色曲线为重物体下落过程轻物体的轨迹，红色曲线表示重物体处于静止时轻物体的轨迹.

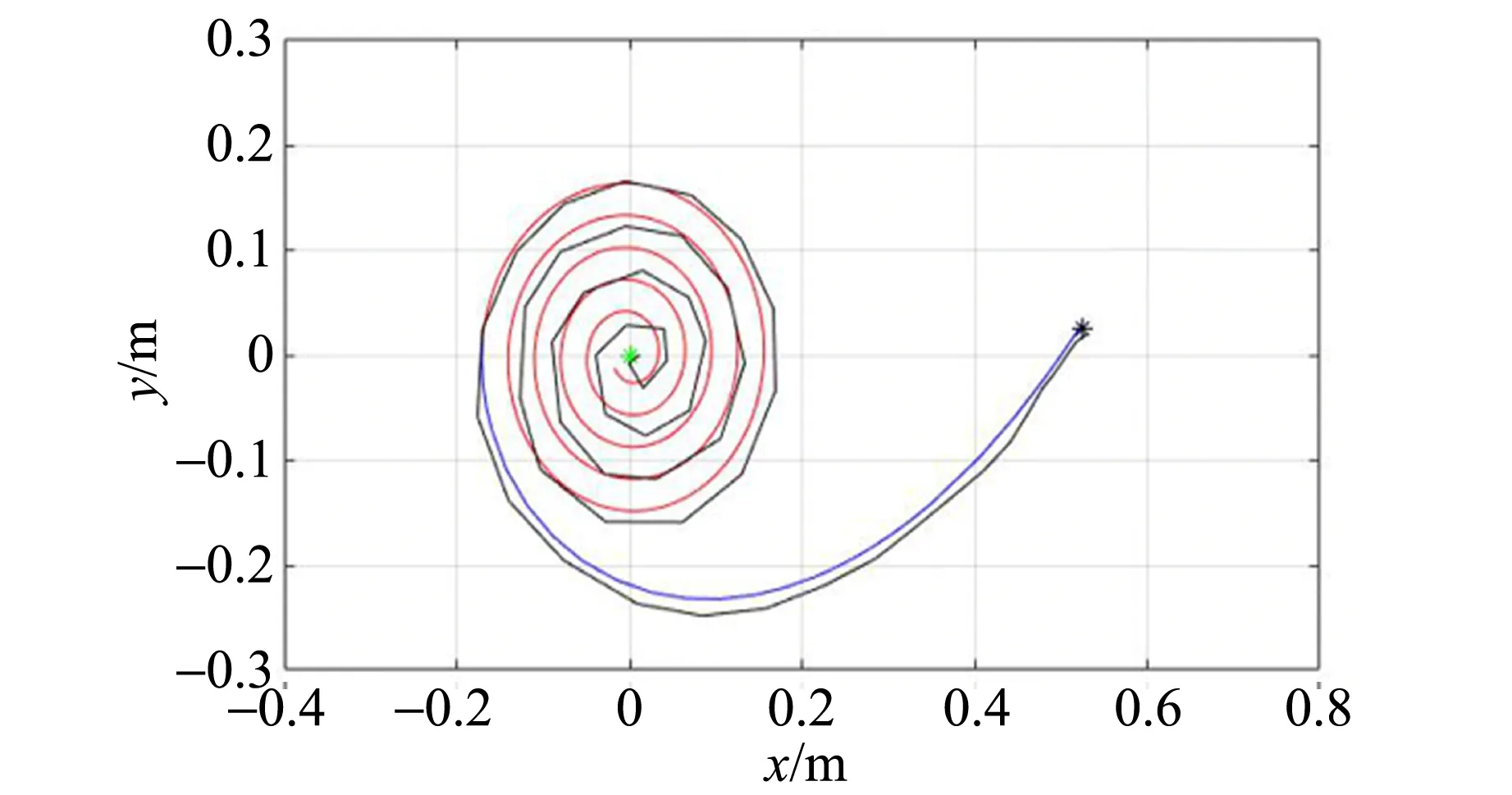
(a)k=0.096，β=93.9°，r0=0.587 m

(b)k=0.326，β=91.5°，r0=0.628 m

(c)k=0.400，β=92.7°，r0=0.525 m图12 实验过程中轻物体运动轨迹与理论轨迹对比

图12(a)为重物下落1次情况，图12(b)为重物下落2次及以上的情况，图12(c)为能阻碍重物体下落的临界情况. 可以发现，对于各种能阻碍重物体落向地面的情况，轻物体运动轨迹与理论仿真轨迹都符合得较好.

3.2 重物体运动速度

首先研究重物体第1次下落过程的速度变化图，理论曲线与实验曲线拟合结果如图13所示，可以看出，在重物体第1次下落过程中，开始轻物体端重力沿绳方向分量较小，可近似为重物体拉着轻物体以加速度

下落，之后随着角度θ的增大，轻物端拉力与摩擦力的合力逐渐变大，当增大到大于重物重力时，重物体开始减速下落，最后停止运动.

(a)k=0.195，r0=0.571 m，β=93.1°

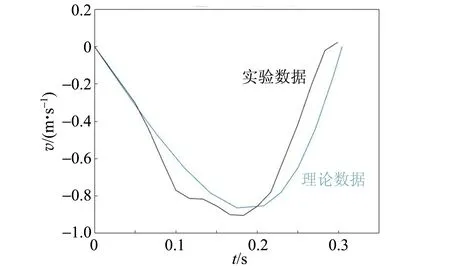
(b)k=0.120，r0=0.525 m，β=92.7°图13 不同实验条件下重物体下落过程的速度变化

3.3 重物体的运动时间

研究了可以形成循环摆过程中，β，r0及k对重物体从开始下落到停止所持续时间Δt的影响. 实验结果与理论结果如图14～16所示. 可以看出，释放角度β越大，初始绳长r0越短，重物体下落持续时间Δt越短. 在质量比k较小时，质量比对下落时间的影响并不显著，在质量比较大时，质量比越大，下落时间Δt越短.

图14 Δt与β的关系(R=4.85 mm,μ=0.192，r0=0.703 m,k=0.250)

图15 Δt与r0的关系(R=4.85 mm,μ=0.192,β=92.3°,k=0.250)

图16 Δt与k的关系(R=4.85 mm,μ=0.192，r0=0.306 m,β=92.8°)

4 结束语

研究了第32届IYPT赛题中循环摆现象. 通过建立循环摆运动的方程组，理论模拟了质量比、初始绳长对轻重物体运动的影响，并进行了实验研究. 结果表明，在轻重物体的质量比k小于0.27～0.43，释放角度β大于68°～90°(均取决于其他初始条件)时，轻物体可以绕杆运动，并可以阻止重物体下落.