基于新型扩张状态观测器的PMSM周期性转速脉动抑制方法

孟淑平，朱家厅，张立娟，左哲清，陈祖希

(北京精密机电控制设备研究所, 北京 100076)

0 引 言

永磁同步电机(Permanent Magnet Synchronous Motors，PMSM)具有功率密度大、效率高、体积小、重量轻、低速性能好、调速范围宽以及可控性好等优点，被广泛应用于高精度机电伺服系统中[1]。然而电机内部以及电机负载侧附加的周期性转矩脉动会造成电机转速中存在较大的周期性脉动，不利于电机高精度的转速伺服和位置伺服控制，同时会导致电机运行过程中负载侧产生机械振动，不适用于对振动噪声有严格要求的场合[2-3]。永磁同步电机中周期性谐波转矩脉动分量产生的原因主要包括：①由磁通谐波、逆变器非线性特性、死区时间、定子相电流硬件检测误差、电机的转速和位置检测误差以及电机负载不平衡等造成的谐波转矩脉动[4]。②永磁同步电机是由永磁体励磁，气隙磁场谐波比较多，使反电动势的谐波也比较多。③齿槽效应会产生齿槽转矩，即永磁体产生的磁场同定子齿槽相互作用产生转矩，引起周期性的转矩脉动。④电机端负载中的周期性分量。

目前减小电机转矩脉动的措施主要分为两类：一类是通过改进电机本体设计来改善电机磁场分布，减小电机转子磁场中的谐波[5-9]，例如采用斜槽、斜极、改进定子绕组分布等措施来减小电机齿槽转矩，这种方法一般会增加电机的生产成本和难度；另一类是采用先进的控制算法，例如迭代学习控制、模糊控制算法、重复控制、构建观测器等，估算出电机中存在的转速或转矩脉动分量，然后采取相应的补偿措施抑制转速或转矩脉动[10-14]。文献[10]利用速度信号对转矩进行前馈补偿，对转速脉动有一定的抑制效果；基于重复控制原理的动态补偿方法，文献[11]提出了在永磁同步电机速度控制环上采用一种重复控制和PI控制相结合的控制方案，以抑制周期性扰动引起的转速脉动。文献[12]采用了迭代学习控制(Iterative Learning Control，ILC)方法来抑制因气隙磁通密度的非正弦分布、电流测量误差和气隙磁阻变化引起的转矩脉动。文献[13-14]同样是采用迭代学习控制算法，在线获得转矩中存在的谐波分量，然后在q轴电流环控制中对估算出的谐波分量进行补偿，从而抑制电机中的转矩脉动，但是迭代学习控制所需要的计算量较大，提高了MCU的运算负荷，不适用于算法复杂的场合。

本文提出了一种基于新型扩张状态观测器的PMSM周期性转速脉动抑制方法。利用周期性信号的微分特性，构建扩张状态观测器，观测出电机转速脉动中的主要周期性分量，利用自抗扰控制算法对其补偿，以消除转速中的周期性脉动。最后进行了仿真和实验验证。

1 PMSM数学模型、周期信号数学模型

面贴式PMSM在旋转坐标系dq轴系下的数学模型为

(1)

(2)

(3)

式中，Rs为电机定子电阻；φ为转子磁链；Ld、Lq分别为d轴和q轴相电感；id、iq分别为d轴和q轴定子电流；ud、uq分别为d轴和q轴定子电压；J为转子转动惯量；B为转子黏性摩擦系数，TL为电机端负载转矩；ωe为电机的电角速度；ω为电机转子角速度；np为磁极对数；ωe=np*ω。

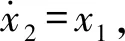
(4)

2 基于新型扩张状态观测器的PMSM周期性转速脉动抑制方法

2.1 传统PMSM的速度伺服控制系统

传统PMSM的速度伺服控制采用矢量控制算法对dq轴进行解耦后，构造内部电流环、外部速度环的双环速度控制策略，控制算法均采用经典PI 控制算法，实现电机转速对给定转速信号的跟踪。简单的PI 控制策略如图1所示。

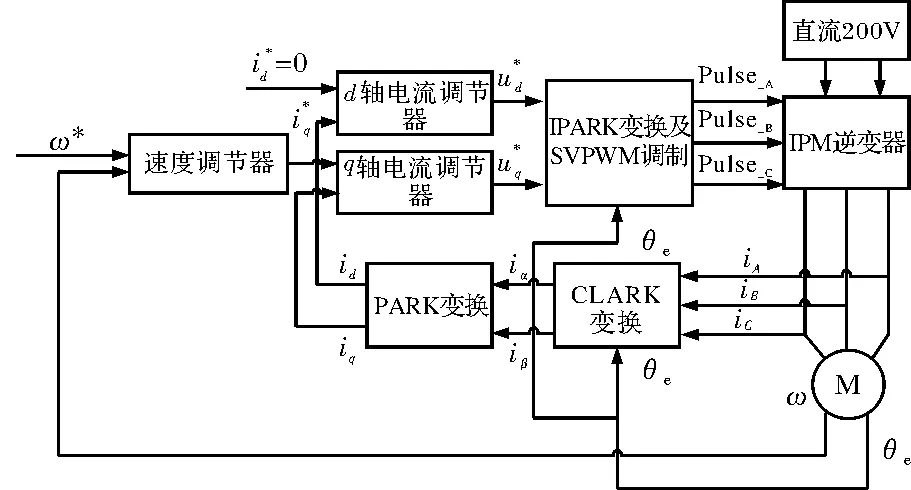
图1 基于PI控制的电机转速伺服控制策略

由于电机自身非线性、齿槽转矩存在、气隙磁场非正弦、控制器硬件非线性或者负载周期性变化的原因，简单的PI控制策略在负载或者给定转速突变的情况下，电机转速会产生大幅突变且调节时间较长，不适用于对转速稳定性要求较高的场合。扩张状态观测器(Extended State Observer，ESO)是自抗扰控制技术最重要的组成部件，其核心思想是：将系统的不确定性(内部摄动)和外部扰动看作一个总扰动并将其扩张成一个新状态,对其进行实时估计，然后通过反馈进行补偿，从而消除总扰动对控制系统的影响[15]。PMSM的机械运动方程式如式(3)所示。令

(5)

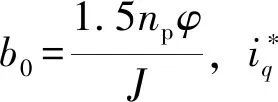
则由机械运动方程式(3)得到的状态方程为

(6)

(7)

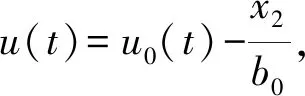
基于ESO的电机转速伺服控制策略如图2所示。

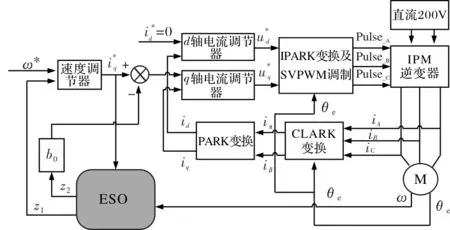
图2 基于ESO的电机转速伺服控制策略

2.2 新型PRD-ESO设计

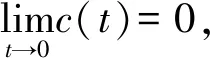
考虑到周期性转矩脉动，则式(3)可改写为

(8)

式中，Td1,Td2,Td3…TdN为不同频率下的周期性转矩分量，N表示谐波次数。

定义扰动如式(9)所示

(9)

将式(9)带入式(8)可得，

(10)

定义状态变量如式(11)所示

(11)

则新的状态方程可以表示为

(12)

构造出线性ESO，如式(13)所示：

(13)

3 稳定性分析

本节对提出的PRD-ESO控制算法稳定性进行分析。以转速中存在一种主要的周期性干扰为例进行稳定性分析，其他类同。

式(13)减去式(12)得到观测误差方程为

(14)

改写成矩阵形式为

(15)

其特征方程为

(16)

为要求过渡过程和稳定性都好，设计特征方程为

(s+p)4=s4+4ps4+6p2s2+4p3s+p4

(17)

式中，-p表示设置的极点，p>0。

一一对应有

(18)

在实际应用中，若转速脉动中同时存在多种主要周期分量，采用如式(13)所示的高阶PRD-ESO观测器，则参数的解算计算量较大。此时可以对各频率的周期性转矩脉动分别利用前述的四阶PRD-ESO分别观测出不同频率下的周期性转矩分量，然后利用自抗扰算法进行补偿，其中速度环的反馈转速以及非周期性转矩的补偿值取不同频率下观测转速和非周期性转矩的平均值。

4 仿真验证与分析

在 Matlab仿真环境下，根据PMSM的控制原理及其参数，搭建永磁同步电机速度伺服控制系统，研究基于新型扩张状态观测器对阶跃型负载以及周期性负载的观测和抑制能力。

电机参数如表1所示。

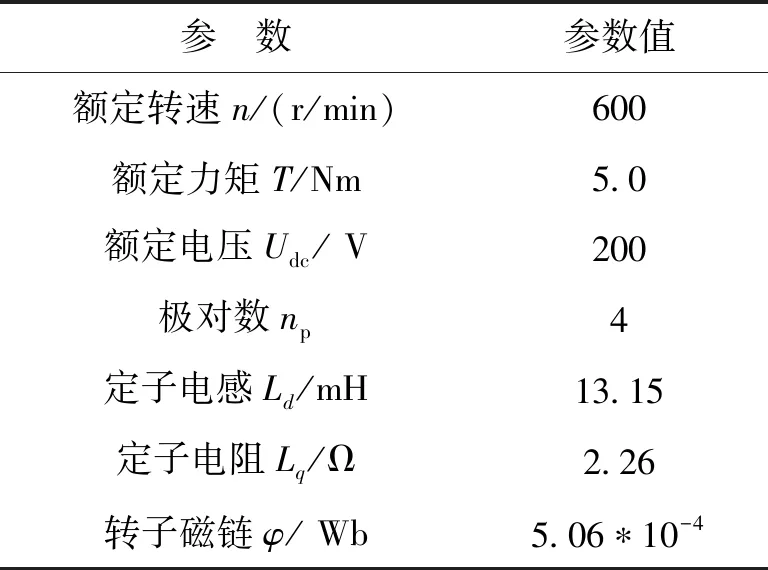
表1 电机参数

在负载端施加不同频率的周期性负载干扰，可以观察到电机转速中产生相应同频次的转速脉动。在负载端叠加频率为80 Hz，幅值2 Nm的周期性负载和t=0.3 s时由0阶跃到3 Nm的阶跃性负载，测量得到的q轴电流和估计出的电机周期性转矩波形及其频谱图如图所示。

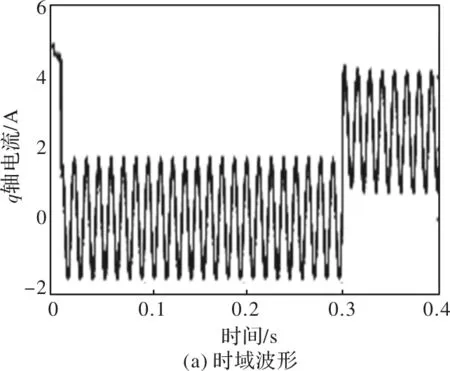
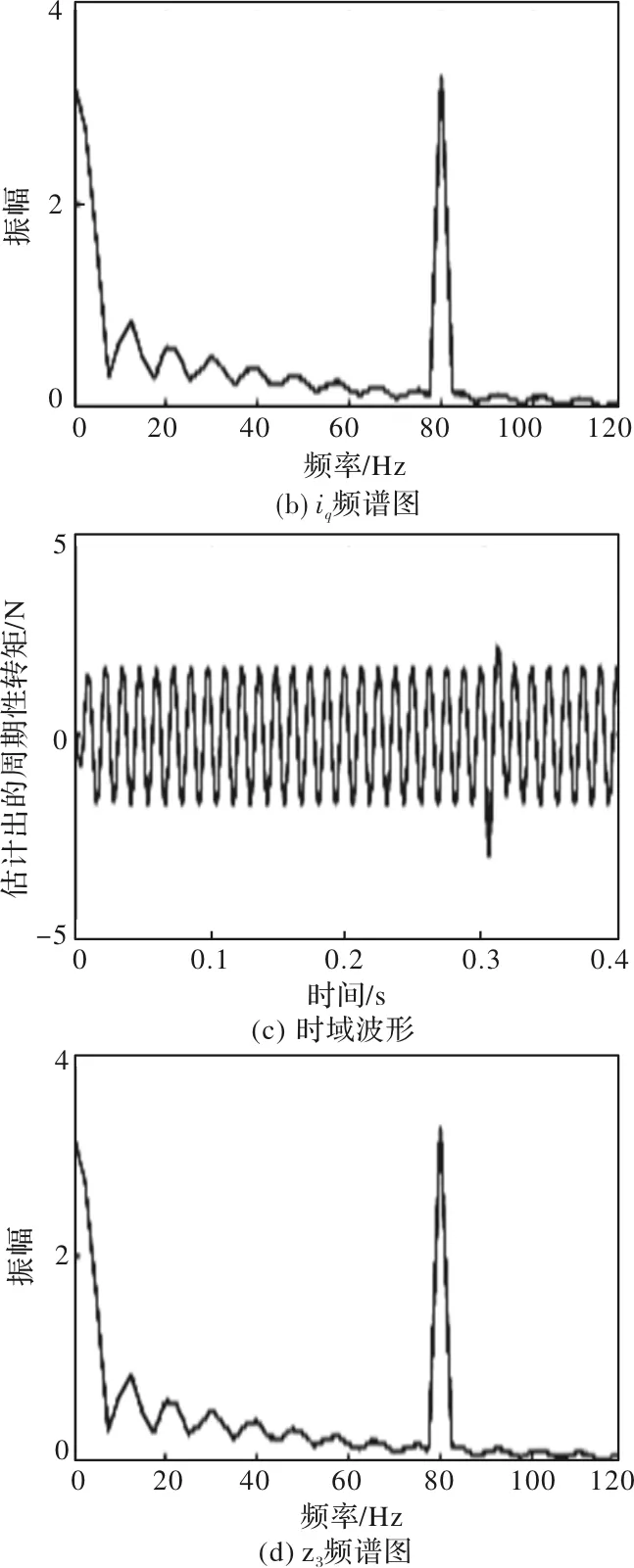
图3 q轴电流和估计出的电机周期性转矩波形及其频谱图

在负载端叠加频率为80 Hz，幅值2 Nm的周期性负载和t=0.3 s时由0阶跃到3 Nm的阶跃性负载，采用普通PID控制策略、采用ESO控制策略、采用新型PRD-ESO控制策略的电机转速波形如图所示。

图4 不同控制策略下电机转速波形对比

从图中可知，在突变性转矩以及周期性转矩的作用下，采用传统PI控制算法，电机转速会发生较大突变，且转速中含有同频次的脉动分量；采用传统ESO算法，可以估计出非周期性转矩分量进行补偿，不能估计出周期性的转矩分量，虽然负载突变时电机转速变化变小，但电机转速中依然存在同频次的脉动分量；采用新型PRD-ESO算法可以有效估算出电机端的周期性负载分量和非周期性负载分量，补偿后，电机转速调节迅速，且转速脉动大幅减小。

5 实验结果与分析

利用0.3 kW 永磁同步电机建立了系统的实验平台，对新型PRD-ESO算法进行了实验研究。该平台由0.3 kW永磁同步电机及其驱动控制单元、200 V 直流电源、CAN总线演示仪以及串口通信模块组成。控制单元采用TMS320F28335 为 主 控 芯 片，PWM的开关频率以及电流环刷新频率均为10 kHz，速度环刷新频率为1 kHz，逆变死区时间设置为2 μs。利用多摩川旋转变压器获得电机转速，通过基于Labview的上位机软件获得待观测量波形，通过串口将数据输出后导入到Matlab中进行信号频谱分析。

首先采用如图1所示的双闭环矢量控制算法控制电机旋转，电流环和速度环均采用传统PI控制，电机给定转速300 r/min和600 r/min，得到电机转速的时域和傅里叶分析波形如图所示。

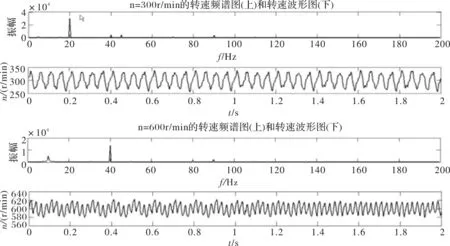
图5 电机转速波形及其频谱图

由图5可知，300 r/min转速下电机机械频率为5 Hz，其中20 Hz为主要谐波频率，600 r/min转速下电机机械角频率为10 Hz，其中10 Hz和40 Hz为主要谐波频率，。

电机转速给定600 r/min时，采用新型PRD-ESO算法对10 Hz和40 Hz等主要周期性转矩分量和非周期性转矩进行观测，如图6所示，图6(a)为对10 Hz谐波频率分量的观测值，图6(b)为对40 Hz谐波频率分量的观测值。图6中横轴为刷新时间，计数5000代表计时1秒钟，图6中周期性转矩和非周期性转矩为放大1000倍的数值，非周期性转矩的微分信号为放大1000/ωd的数值。

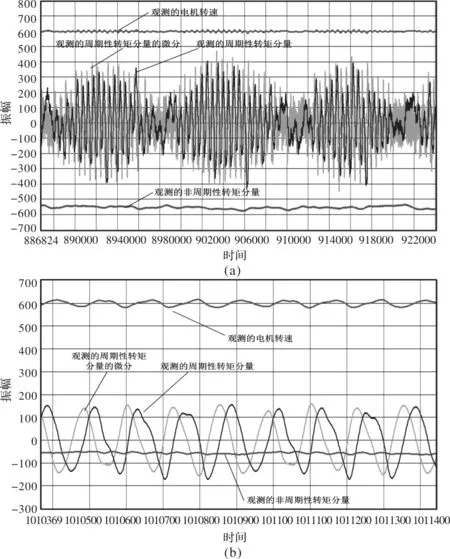
图6 采用新型PRD-ESO算法的观测值

给定转速从300 r/min阶跃变化到600 r/min，采用传统ESO控制得到的电机转速和采用新型PRD-ESO得到的电机转速对比如图7所示。对图7中的升速过程和降速过程进行局部放大，如图8所示，其中图8(a)为基于传统ESO控制算法的给定转速阶跃变化时的动态曲线，图中的Tr表示电机转速跟踪给定转速300 r/min变化到600 r/min所需的时间，约为0.04 s，图8(b)为基于新型PRD-ESO控制算法的给定转速阶跃变化时的动态曲线，图中的Tf表示电机转速跟踪给定转速600 r/min变化到300 r/min所需的时间，约为0.04 s。

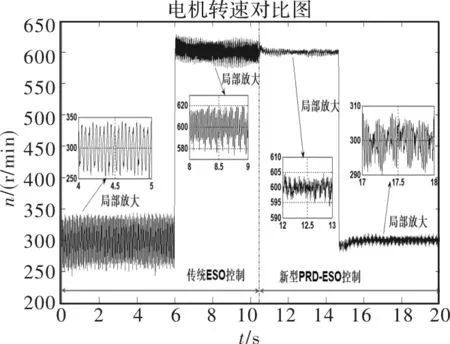
图7 电机转速波形对比

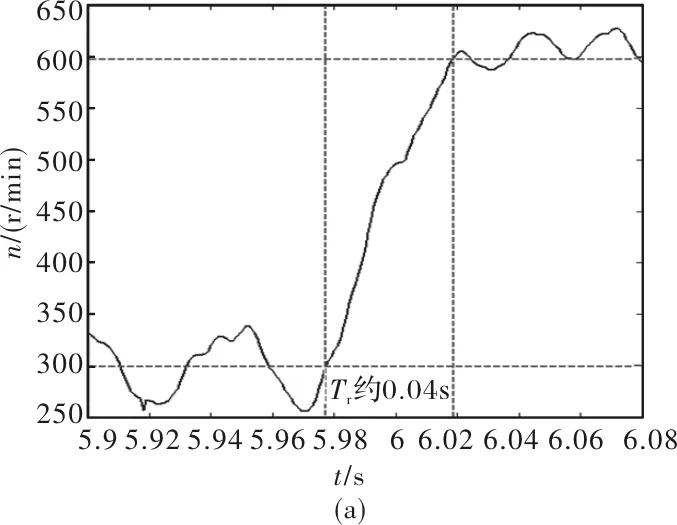
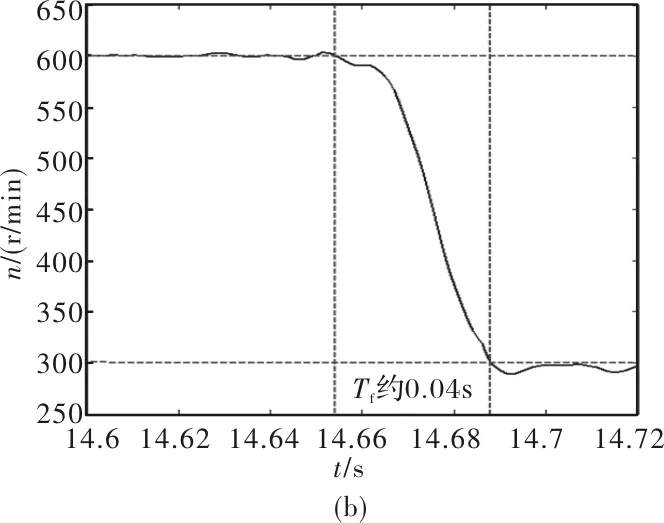
图8 电机升降速动态特性对比

由图7、图8可知，采用传统ESO控制时，300 r/min下的转速波动为±48 r/min，600 r/min下的转速波动为±22 r/min，切换到新型PRD-ESO控制时，300 r/min下的转速波动为±9 r/min，600 r/min下的转速波动为±4 r/min，转速脉动改善了82%，传统ESO算法的Tr时间和新型PRD-ESO算法的Tf时间均在0.04 s左右，说明采用PRD-ESO算法后系统的动态性能没有受到影响。

6 结 语

(1)基于新型扩张状态观测器的转速脉动抑制方法，能有效估计出周期性转矩分量和非周期性转矩分量。

(2)采用自抗扰算法对估计出周期性转矩分量和非周期性转矩分量补偿，有效抑制了转速中的周期性脉动，脉动改善可达82%，且在电机端负载突变时电机转速可以迅速调节。

(3)基于新型扩张状态观测器的转速脉动抑制方法不影响系统的动态性能，在给定转速阶跃变化时，系统响应迅速。