基于时延特性建模的多断面短时交通流预测

刘小明，田玉林，唐少虎，尚春琳，魏 路

(1.北方工业大学城市道路交通智能控制技术北京市重点实验室，北京100043；2.北京联合大学城市轨道交通与物流学院，北京100101)

0 引 言

近年来，城市化进程逐渐加快，交通需求快速增加，城市道路交通压力不断升高，交通信号主动控制成为缓解城市交通问题的重要手段之一，交通路网短时交通流预测是实现主动优化的关键.道路交通流预测是车辆路径规划的重要参考，可以帮助出行者做出更好的路径选择；对交通管理也起着较大作用，可以及时、主动地将路网时间和空间资源进行按需分配，提高交通出行效率及路网运行的稳定性.

交通流运行具有明显的复杂性和不确定性，获取其准确的预测结果有一定难度.国内外学者对此进行大量的研究和探索，取得一定的成果.广泛使用的预测模型有：历史平均模型、时间序列模型、状态空间模型、神经网络模型、非参数回归模型、支持向量机模型等[1]，但多数模型是利用目标路段的历史交通流数据，未能充分利用路网内其他相关路段的交通流信息，对交通流传输特性参数提取不充分，会在一定程度上影响预测结果.

根据交通数据来源点位置不同，将交通流预测分为单断面预测和多断面预测.单断面交通流预测仅对本断面的交通流特性进行建模，忽略了路网中不同断面之间的关联信息，模型鲁棒性通常较差，易受噪声干扰.多断面交通流预测利用干道流量关键点或路网相关联断面数据，引入更加丰富的信息，有利于模型做出更加准确的预测.现有多断面交通流预测方法基本是将表征路网结构的空间信息和历史时间信息作为网络输入，通过分析数据的时空特征，实现对不同断面、不同时刻的数据融合，忽视了对不同断面流量之间时延特性的建模.邹东[2]利用交通流数据的时空相关性提出基于Elman神经网络算法.Wu[3]分别利用卷积神经网络和循环神经网络处理空间和时间信息.Lin[4]将大规模共享单车网络建模成图，利用图卷积神经网络预测节点需求.为加速神经网络的收敛速度并降低网络学习难度，Dai[5]提出对数据进行去趋势的方法，将流量随时间变化的趋势及相对趋势的变化进行分离.

实际情况中，不同断面之间往往相距一定距离，密切相关的断面之间，流量特性在时间维度上存在很强的相似性，但也伴随一定的时延，故忽视时延研究流量数据在时间和空间上的相似性是不完善的.对此，本文对不同断面流量的时延特性进行建模，在时间和空间维度上对数据段进行相似性度量，对不同断面数据进行融合；挖掘不同断面历史数据中的有效信息，提升流量预测的精度.

1 路网交通流传输时延特性分析

交通流运动过程是包含随机因素的复杂过程，增加了实现交通流实时预测的难度.时延特性针对目标交通流经过上下游多断面的时间差展开，从微观模型分析，车辆在路网中的运动形态分为连续交通流和非连续交通流.在路段中车辆以连续自由流的形式运动，经过有信号控制交叉口后，被分割成多股车流交替放行.如图1路网所示，来自不同路段的车流经过信号分隔以后，组成新的交通流进行传输，多股交通流经过上游断面传输到下游断面时，交通量的总量基本保持不变，即近似有QIN=QOUT，QIN表示上游三个断面(断面1、2、3)的流量和，QOUT表示下游断面(断面4)的流量和，而下游断面的流量特性同上游多断面间存在明显时延.考虑到下游目标断面与上游多个断面之间的流量关系可视为下游目标断面同上游各单断面关系的叠加，为便于对上下游断面的时延特性获得直观的感受，图1路段中交通流传输示意图简化分析上下游断面间的流量关系，利用仿真数据通过曲线拟合建立流量随时间变化情况.图1中，t1,t2表示上游断面主要交通流的经过时刻，t3,t4表示对应的交通流到达下游的时刻.

图1 路段中交通流传输示意图Fig.1 Diagram of traffic flow transmission

交通流在路段内传输时，车辆速度随车流密度的增加而减小，引起传输时延的增加.由路段内速度u(t)与密度k(t)随时间t的变化关系及路段模拟数据，采用曲线拟合的方式，拟合出目标路段内交通流传输时延与车辆密度的变化趋势图，如图2所示，其中，df为自由流速度对应的路段行驶时间.

式中：u(t)，k(t)分别为路段速度、密度分布函数；uf为自由流速度；kj为阻塞密度；li为路段i的长度；ti,b，ti,e分别为车辆在路段i上进入、驶出时刻；di为路段i上的时延.

图2 路段中时延与密度变化趋势图Fig.2 Trend diagram of traffic flow transmission delay and vehicle density

从宏观模型方面分析，交通流的传播特性可以描述为包含交通流密度、速度、流量三者之间稳态关系的交通流模型[6].对于路网而言，同质性路网内车辆密度(或路网内车辆数)和路网通行能力之间存在宏观基本图(Macroscopic Fundamental Diagram，MFD)，如图3 所示，其中，D(n)为路网内车辆总传输时延随密度变化的函数，ncr为路网通行能力最大时对应的路网内车辆数.nncr时，即路网内车辆数超过最大值，路段内车辆密度过高，交通流传播速度降低，交通流在路网中的总时延升高.确定不同路网的Cmax、Cok、Cmin、nmax，拟合出路网MFD曲线，采用三次函数近似描述为

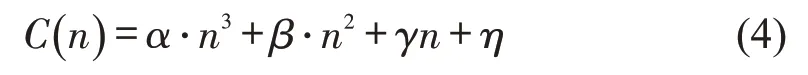
式中：C(n)为路网通行能力；n为路网内车辆数；α、β、γ、η为模型待定系数.

通过建立路网及相应模拟数据，采用曲线拟合的方式拟合出路网通行能力C(n)与路网总时延分布函数D(n)之间的变化趋势关系，如图3所示.

由上述分析可知，交通流传输时延与路段交通量密切相关，仅考虑断面距离、交通流排队消散特性[7-9]等因素无法实现传输时延的精确描述.本文利用多断面流量数据，建立目标交通流在运动过程中的动态跟踪模型，预测相近断面间交通流传输的最佳时延，结合历史数据，对流量变化进行学习，改善交通流预测对数据本质挖掘不足，引起动态跟随效果不理想的状况，优化基于时延特性的交通流预测效果.

图3 路网中时延特性分布示意图Fig.3 Distribution diagram of traffic flow transmission delay

2 基于时延特性建模的交通流预测模型

2.1 流量数据时延特性建模及流量初步预测

不同断面之间流量时延特性主要体现为流量在时间维度上的分布存在一定的延迟，即

式中：fa和fb分别表示断面a和断面b的流量随时间的变化；d(t)表示两断面之间时延随时间变化的函数.

时延特性建模的相似性度量及流量初步预测过程如下：

首先，对输入数据进行切分和重组，捕捉目标断面流量和其他断面流量之间潜在的时延特性.为描述各断面某一时刻的短时流量，选取以当前时刻为结束时刻，长度为k的连续子序列作为此时该断面的流量特征.子序列长度选取需综合考虑输入数据的长度及相似度比较的可靠性.对于确定长度的输入，选取较短的子序列能够获得对更长时延范围的建模，但会减弱相似性比较的鲁棒性，使其易受到噪声数据干扰.对于目标断面Si(i为该目标断面的序号)，仅考虑其末尾时刻的流量特性，即

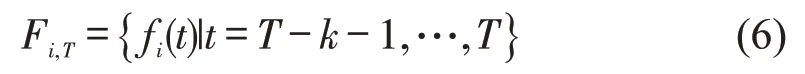
式中：fi(t)为断面Si流量随时间的函数；T为输入时间序列的末尾时刻.

对于其他断面Sj(j为该断面的序号)，通过遍历时延列表，对其数据进行切分，得到不同时刻的短时流量特征为

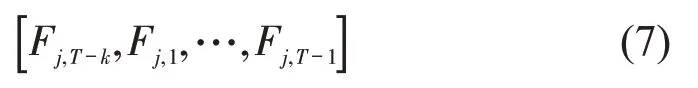
然后，综合余弦相似度和幅度相似度，建立目标断面末尾时刻与其他断面各时刻短时流量描述之间的相似性度量矩阵S∈ℜ()m-1×l，其中，m为断面总数，l为对每个断面输入进行切分得到的子序列个数.对任意的两个短时流量特征a和b，定义他们之间的相似度为

对某一断面不同时刻的流量数据，选择相似度最大的一个作为其同目标断面的最佳匹配，预测得到断面Sj同目标断面Si流量数据的最佳时延为

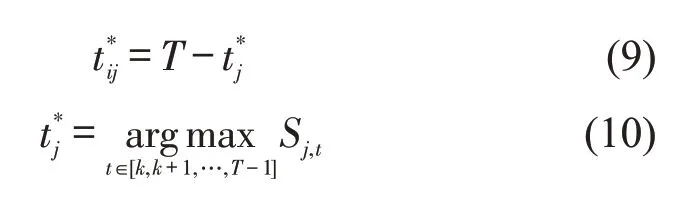
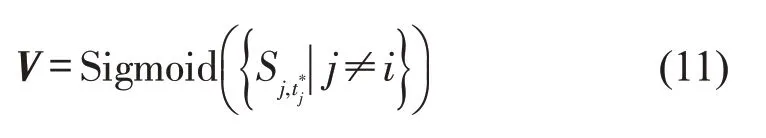
为保证目标断面未来时刻流量预测在幅度上的合理性，对不同断面的最佳匹配进行能量归一化，定义能量增益为

式中：E是集合中所有元素形成的列向量，代表各断面与目标断面的最佳匹配子序列的能量，为断面Sj在时刻的短时流量特征.通过能量增益对最佳相似度向量进行能量归一化，用于目标断面的流量预测.能量归一化后的最佳相似度向量为

对目标断面未来时刻的初步预测表示为

式中：Q为集合中所有元素构成的列向量，表示不同断面同目标断面最佳匹配时刻的下一时刻流量值表示断面Sj在1 时刻的流量.

图4 为本算法计算过程，断面1 表示目标断面，断面2 和3 为其临近断面.选择子序列长度为5，对断面1的输入数据进行截取，将最后5个时刻作为目标断面的末尾时刻流量特性(断面1中方框加粗的序列).将其他断面的输入数据以步长为1，切分成长度为5的子序列集，并与目标断面末尾流量序列进行相似性度量.各断面内部选择相似性最高的子序列(断面2、3中方框加粗的序列)，同时对各断面的最大相似度进行能量归一化.利用归一化后的相似度对各断面最相似子序列的下一时刻流量(数字加粗的数据)进行加权求和，从而实现对目标流量的初步预测.

图4 基于时延特性建模的相似性度量及流量初步预测示意图Fig.4 Schematic diagram of similarity measurement and preliminary prediction

2.2 基于LSTM的多断面交通流预测模型

利用2.1 节中对目标断面流量的初步预测及原始数据，构建递归神经网络(RNN)模型获得更加精确的预测值.在数据计算和学习过程中，由于交通流时延特性影响，序列的时间跨度使隐含层中记忆值较小，造成梯度消失问题，本文将LSTM 单元引入RNN 链式结构中加强预测网络的记忆能力.单层LSTM示意图如图5所示，其中，xt表示该层输入的t时刻的数据，ht表示该层输入的t时刻的隐藏信息，σ和tanh 分别表示sigmoid 和tanh激活函数.我们堆叠了3 层LSTM 网络.第1 层网络的输入为原始数据和初步预测值，其余各层网络输入为上一层的隐含层输出.将初步预测得到的标量直接串联到原始数据的末尾，组合成新的数据.为保持对比实验的公平性，对组合之后的数据裁剪掉其开始时刻的流量值，使重构后的数据与原始数据在长度上保持一致，使两者能够共享一个结构完全相同的神经网络.将最后一层的最后一个LSTM单元的状态输出作为最终预测值.

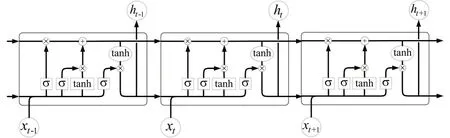
图5 单层LSTM 网络示意图Fig.5 Diagram of one-layer LSTM network

3 实验分析

3.1 数据来源及预测结果

为验证所提方法的有效性，在公开数据集PeMS(美国加利福尼亚运输部性能测量系统)进行实验验证，该数据集通过埋藏在道路中的线圈探测器获取车辆信息，数据采集间隔设置为5 min.选择2016年1～6月共计180 d 的车流数据作为研究对象，其中，4/5 的数据用作训练，1/5(约36 d)用作测试.

实验中，选择城市干道主方向上连续的4个断面作为实验对象，其上下游关系按照断面标号从上游到下游进行排列，各断面间相对距离在1.3～3.2 km，干道交通流为主要流量来源.将相邻的20个时刻数据作为一个样本，共得到51 820个数据，其中，训练集样本数为41 456，验证集样本数为10 364.实验中使用的数据仅含断面的流量特征.综合实际输入数据长度及相似度比较的可靠性，将子序列长度设置为10.仅使用LSTM 模型的预测结果与本实验结果进行对比.为便于对比预测的细节效果，截取其中连续5 d的真实流量强度与预测值，对流量强度进行归一化处理.4 个断面的实际预测效果如图6～图9 所示，其中，“LSTM”仅使用LSTM网络进行交通流预测，“LSTM+Delay”在时延特性建模模块初步预测的基础上，使用LSTM进行进一步预测.

3.2 效果分析

使用均方根误差(ERMSE)、平均绝对误差(EMAE)和平均绝对百分比误差(EMAPE)这3 种指标对预测结果进行量化分析.3种预测方法的误差及对比如表1所示，其中，“Delay”仅使用时延特性建模模块进行初步预测，Xp为编号为p的预测值误差，Xˉ为预测平均误差，z为预测值总数.

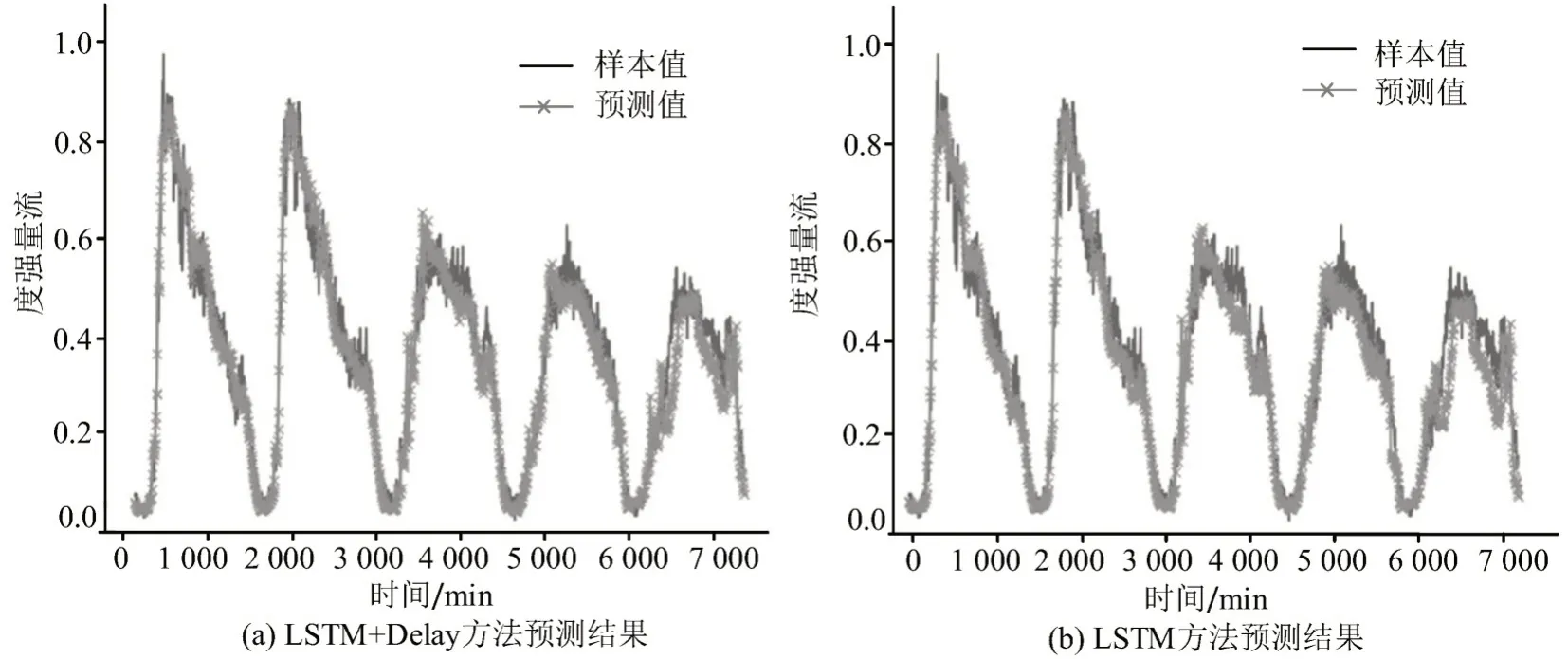
图6 断面1 预测结果可视化Fig.6 Prediction results of traffic section 1

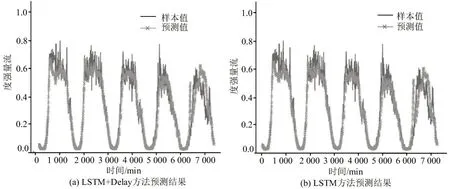
图7 断面2 预测结果可视化Fig.7 Prediction results of traffic section 2

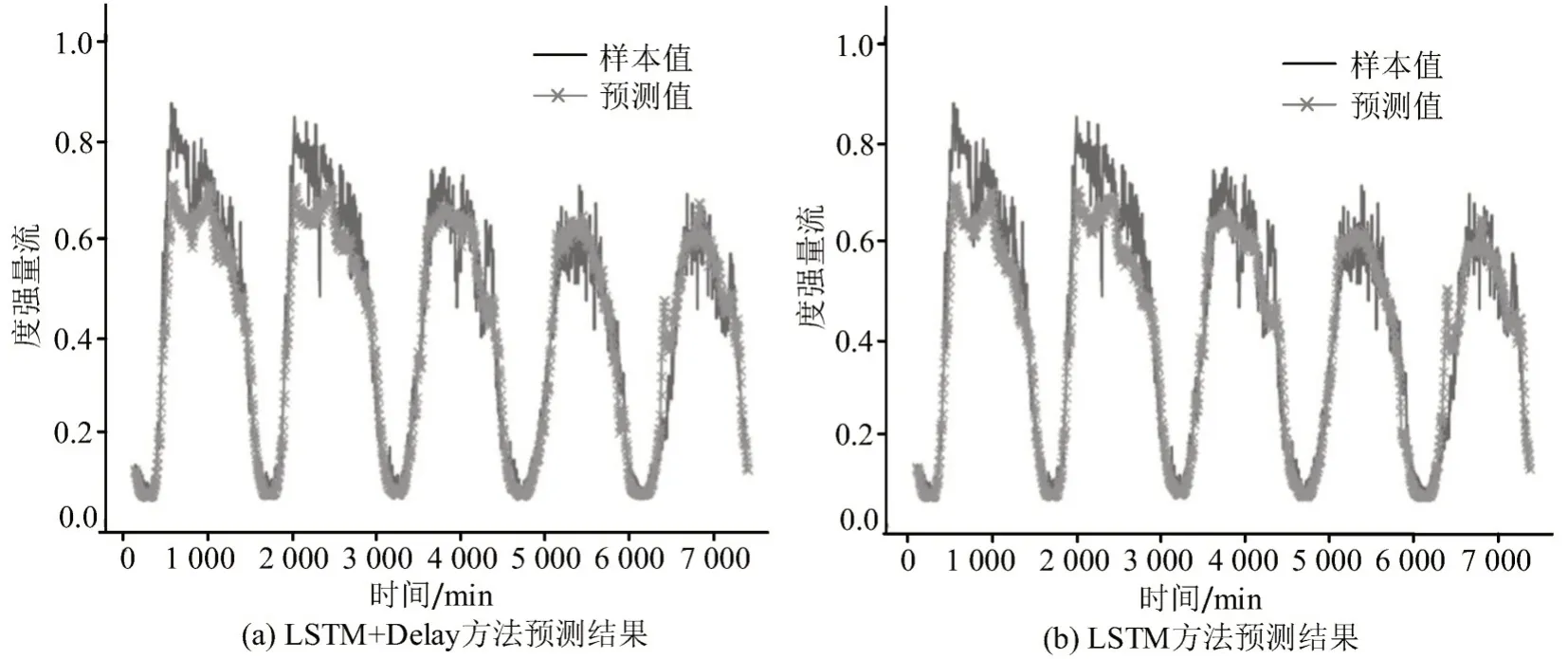
图8 断面3 预测结果可视化Fig.8 Prediction results of traffic section 3

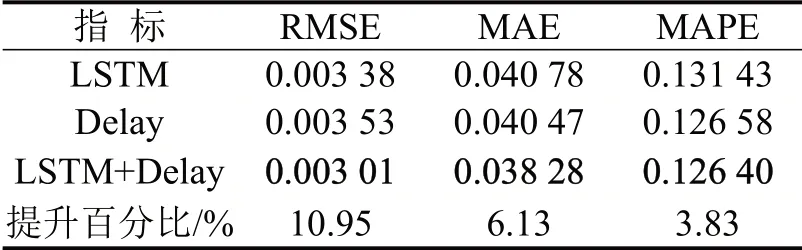
表1 预测结果对比Table 1 Prediction result

由实际预测数据的误差统计结果可知，单依靠时延特性建模的交通流预测方法已能够提升部分短时交通流预测性能，将时延特性与LSTM 网络进行组合预测时，其预测误差可以明显改善，充分说明时延特性对预测结果可靠性的影响，表明本文方法是一种有效的交通流预测方法.

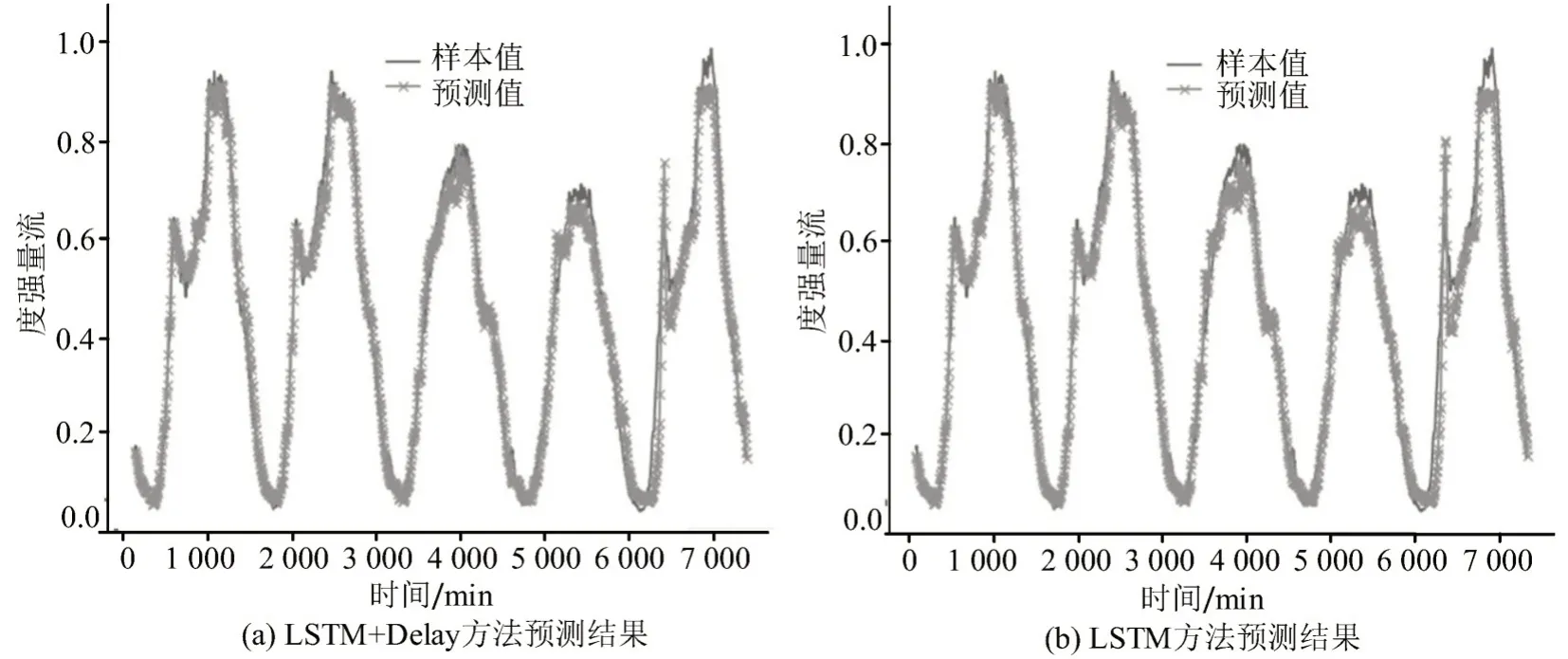
图9 断面4 预测结果可视化Fig.9 Prediction results of traffic section 4

4 结 论

本文在考虑交通流时延特性的理论框架下，对路网中交通流密度与时延系数之间的存在性关系和变化趋势进行分析，同时结合实际流量数据，建立了数据的相似性度量方法，实现了基于流量匹配的多断面时延系数求解及断面流量的初步预测.最后通过搭建三层LSTM 网络的多断面交通流预测模型，实现了基于时延特性的短时交通流预测，通过对比预测结果，证明了本方法的有效性.