共享自动驾驶汽车经营策略优化分析

田丽君，刘会楠，许 岩

(1.福州大学经济与管理学院，福州350116；2.内蒙古财经大学统计与数学学院，呼和浩特010070)

0 引 言

道路交通拥堵问题日益严重，拥堵不仅给出行者带来负效用，造成的无效燃油消耗及汽车尾气排放对生态环境也产生了很大影响，突显了鼓励公共交通出行或合乘出行的紧迫性，以及进行交通管控的必要性[1].

1969年，Vickrey[2]首次应用确定性排队理论得到使所有出行者具有相同交通费用的内生出发时间选择模型，被称为瓶颈模型，因其可以获得清晰的解析结果，广泛用来研究各种场景下的交通均衡及优化问题.Tabuchi[3]研究了地铁票价处于边际、平均成本定价和最优票价时地铁与具有瓶颈公路的模式划分及福利情况.田琼等[4]仅考虑早到成本，得到不同制度下的地铁票价和出行分布，黄海军等[5]在其基础上考虑晚到成本和寡头情形，对其进行扩展.Huang[6]引入两类异质通勤者，比较固定需求时4种定价机制下，地铁和公路模式划分情况.Xiao等[7]研究了不同停车位约束下通勤者选择GP车道和HOV车道的均衡问题，并讨论了社会成本最小化时的最优车道容量和停车位供应.

随着人工智能领域的快速发展和无人驾驶汽车技术的出现，自动驾驶汽车逐渐走入人们的视野.Van den Berg 等[8]分析了自动驾驶汽车仅影响道路容量、仅影响通勤者单位时间价值及同时产生影响3 种情况下普通汽车和自动驾驶汽车(AV)的均衡成本，并研究不同AV 供应策略下AV 均衡占比情况.Meyer 等[9]提出自动驾驶汽车会增加道路容量和城市可达性，在高峰期自动驾驶车队将满足大部分运输需求，在一定程度上取代公共交通需求.而共享自动驾驶汽车(SAV)作为一种新型的出行模式，为合乘出行提供了一条新思路.Tian等[10]考虑依赖于旅行时间的燃油消耗，研究存在停车约束的动态出发模式和SAV 内生渗透率，得到系统最优时SAV 容量及停车位数量.Pakusch 等[11]提出SAV 会提高乘客的舒适度和整体便利性，相比传统汽车合乘，SAV对用户更有吸引力.

本文研究SAV 与普通车共存背景下，SAV 公司如何根据运营目标选择经营策略，如何影响通勤者出行决策及系统总成本或净收益.假设公路上存在一定数量的普通车独驾通勤者①假设独驾通勤者为有车族，与无车族为异质用户，由于生活习惯或者厌恶地铁拥挤或合乘出行，无论出行成本如何，他们总会选择独驾出行.，在SAV公司不同的运营目标下，分析剩余无车通勤者的交通方式选择及SAV 公司的最优经营策略，比较不同情景下SAV发车数、系统总成本或系统净收益，公司利润等指标.

1 模型描述

假设居住地和工作地之间存在两条并行线路提供交通服务，一条为高速公路，一条为地铁.每天有N位通勤者从居住地到工作地上班，其中，N0位通勤者是有车族，总是选择高速公路独驾小汽车上班.有一个共享自动驾驶汽车(SAV)公司为无车族提供通勤服务.无车族有两种可选出行方式：乘坐SAV，享受相对舒适的出行环境，但需承担因合乘带来的额外成本；乘坐地铁，但需忍受地铁拥挤.所有通勤者工作开始时间均为t*，都希望能准时达到，否则会产生早到或晚到延误成本.设地铁容量无限，无论地铁车厢多拥挤，均会准时到达，故地铁通勤者无延误成本；普通小汽车与SAV同时在高速公路上行驶，受高速公路出口处通行能力s的制约，如果车辆到达率超过通行能力s，就会形成排队，故不能保证所有高速路通勤者都能准时到达，高速路通勤者存在延误成本.设Q(t)为高速路在t时刻的排队长度，车辆在高速公路上的通勤时间为T1+Q(t)s，其中，T1是自由流行驶时间，Q(t)s是瓶颈前的排队等待时间.SAV 公司会根据实时市场需求提供车辆，由市场决定发车数量，设早高峰SAV 公司共需提供l辆车，每辆SAV的容量均为ρ，为简单起见，假设所有SAV均满载，乘坐SAV的人数为NS=lρ，乘坐地铁的人数为NT=N-N0-lρ.

采用经典瓶颈模型[2]计算高速路通勤者的个体出行成本[3].令②β,γ 分别为单位早到时间和晚到时间的惩罚成本.，有车族个体均衡出行成本③为简单起见，不考虑车辆购置这一沉没成本.对于有车族，无论市场上其他出行方式是否更加低廉，总是选择自驾出行.为

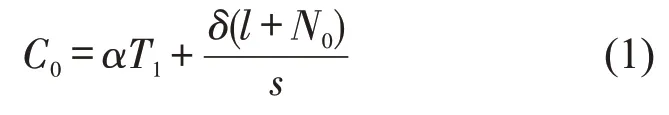
SAV通勤者个体均衡出行成本[10]为

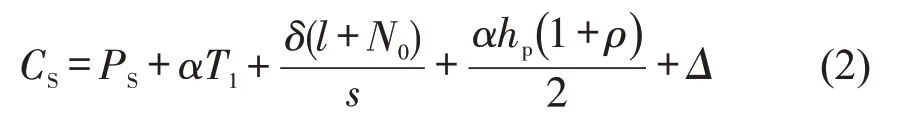
式中：PS为乘坐SAV 需要支付的票价；α为通勤者的时间价值；hp为每接一个乘客的时间，第1个乘客经历的接人时间为hpρ，最后一个乘客经历的接人时间为hp，平均接人时间为(1+ρ)hp/2[10]；Δ为因缺乏私密性产生的不舒服成本.式(2)第2 项和第3项与式(1)一致，由常态行驶时间成本、排队成本和延误成本组成，第4项为接人成本.

地铁通勤者出行成本由地铁票价、通行时间消耗和拥挤成本构成，个体均衡出行成本①为简化分析，本文采取线性拥挤函数，即g(NT)=NT.为

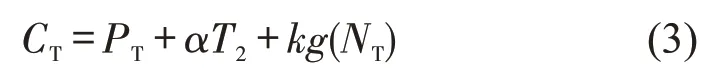
式中：PT为地铁票价；T2为地铁通勤时间；k为单位拥挤程度带来的不舒服成本；NT为乘坐地铁的人数；g(NT)表示车内拥挤程度.

在均衡状态下，无车族通勤者的个体出行成本均相等，即CS=CT总成立.令T1=T2=0 ，求解CS=CT得到均衡时市场决定的SAV 数量，以及选择两种出行方式的人数NS和NT为

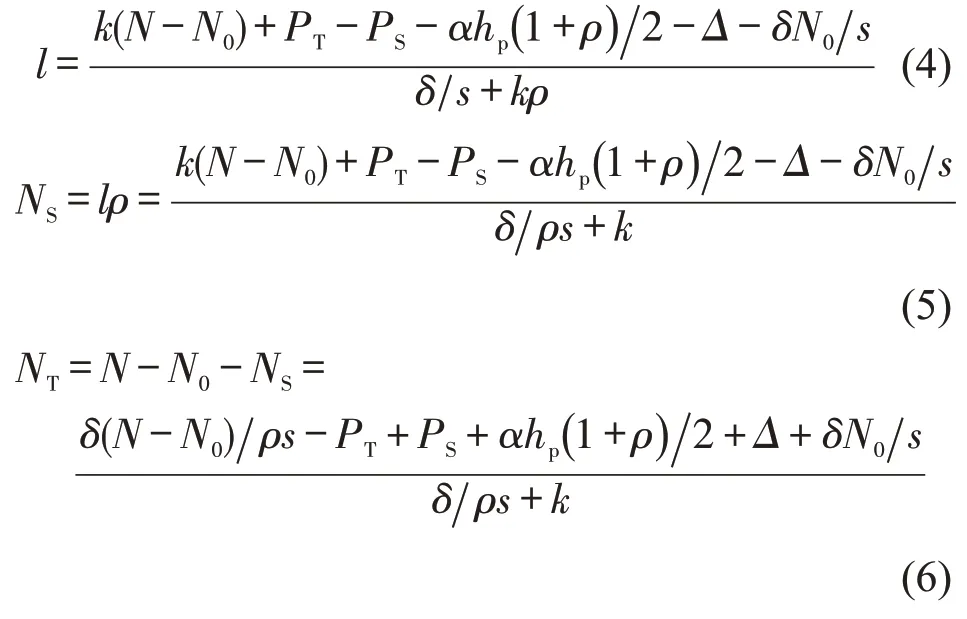
可以看出，当SAV 公司确定经营策略(票价水平PS和SAV容量ρ)后，便可得出市场均衡时需要的SAV发车数l，以及方式划分的结果和个体出行成本.由式(4)易得，SAV发车数l随票价PS和容量ρ单调递减.令表示均衡状态时无车族的个体出行成本，=CS=CT，f1和f2分别为SAV和地铁的可变成本，F1和F2分别为运行一辆SAV和地铁的固定成本(折算到一个高峰期内，并由SAV公司或地铁公司承担的费用).系统总成本为

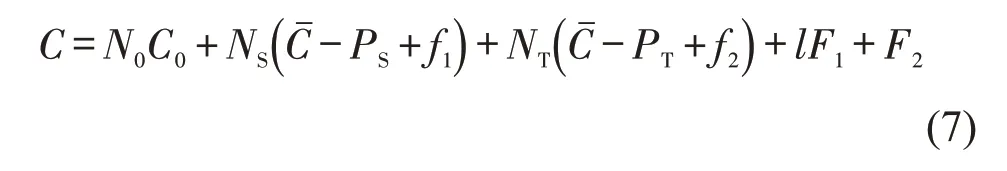
SAV公司的净利润为

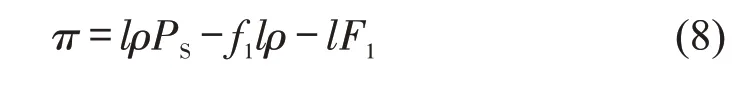
2 固定需求下均衡结果

2.1 系统总成本最小化

假设SAV 公司由政府所有，经营目的是为通勤者提供便利，通过合理的服务水平与地铁公司竞争，即通过票价设定和选择适当的SAV 容量实现系统总成本最小化.用上标“fs”表示固定需求下系统最优结果.

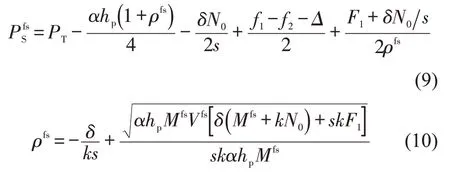
式中 ：Vfs=2k2s(N-N0)+δαhp-k(sαhp+2δN0+2sΔ)-2ks,Mfs=k(N-N0)-f1+f2T.

从式(9)和式(10)可以看出，是ρfs的函数，但表达式比较复杂，无法确定明确的解析解，通过数值算例进行验证.当和ρfs给定后，代入式(4)～式(6)，得到固定需求下系统最优时市场决定的SAV 数量lfs和方式划分结果与，以及由式(7)和式(8)得到系统总成本Cfs和SAV 公司利润πfs.

2.2 SAV公司利润最大化

SAV 公司为私人所有并垄断经营时，其经营目的是获得盈利，即通过调整经营策略实现利润最大化.用上标“fp”表示固定需求下SAV 公司追求利润最大化的结果.

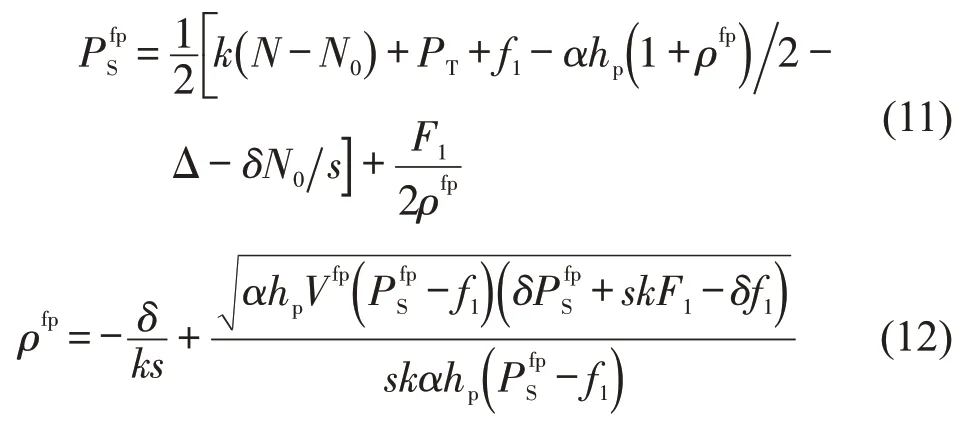
式中：.

同理，当和ρfp给定后，代入式(4)～式(6)，得到固定需求下SAV公司利润最大化时市场决定的SAV 数量lfp和方式划分结果与，以及由式(7)和式(8)得到系统总成本Cfp和SAV 公司利润πfp.

3 弹性需求下均衡结果

交通需求与出行成本具有对应关系，一般成本越高，需求越低.假设需求函数的逆函数为D-1(x)，为单调递减函数.系统净收益为

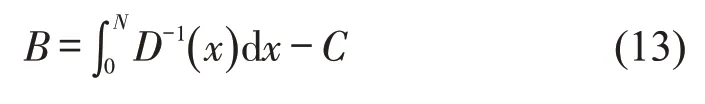
3.1 净收益最大化

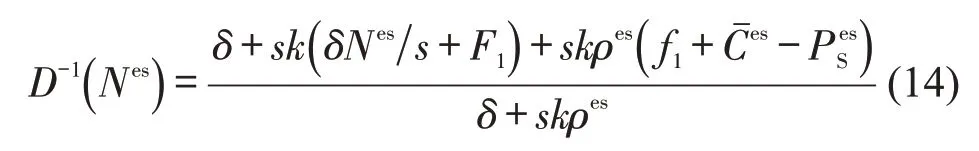
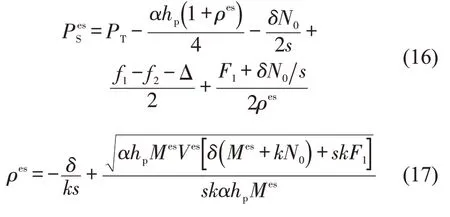
式中：Ves=2k2s(Nes-N0)+δαhp-k(sαhp+2δN0+2sΔ)-2ks(T),Mes=k(Nes-N0)-f1+f2T.

同样，得到最优的，ρes，Nes，les，，，Ces，Bes和πes.

3.2 SAV公司利润最大化

用上标“ep”表示弹性需求下SAV公司追求利润最大化的结果.根据需求平衡关系

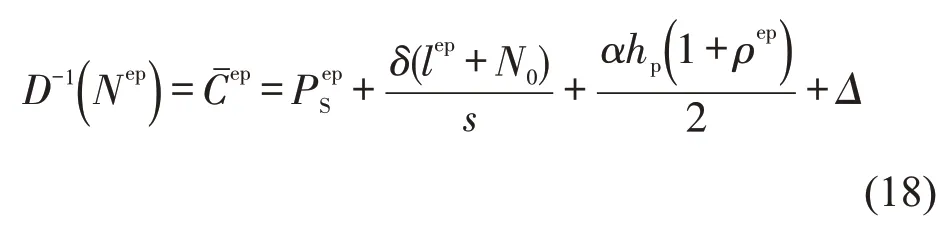
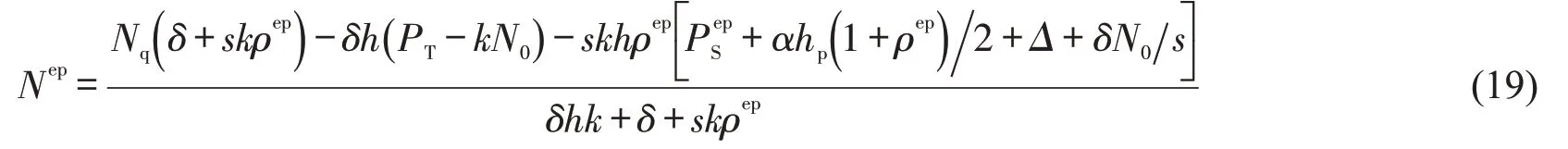
将式(19)代入式(4)，得

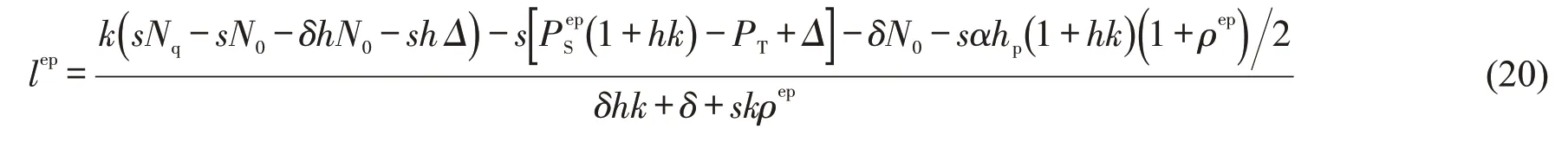
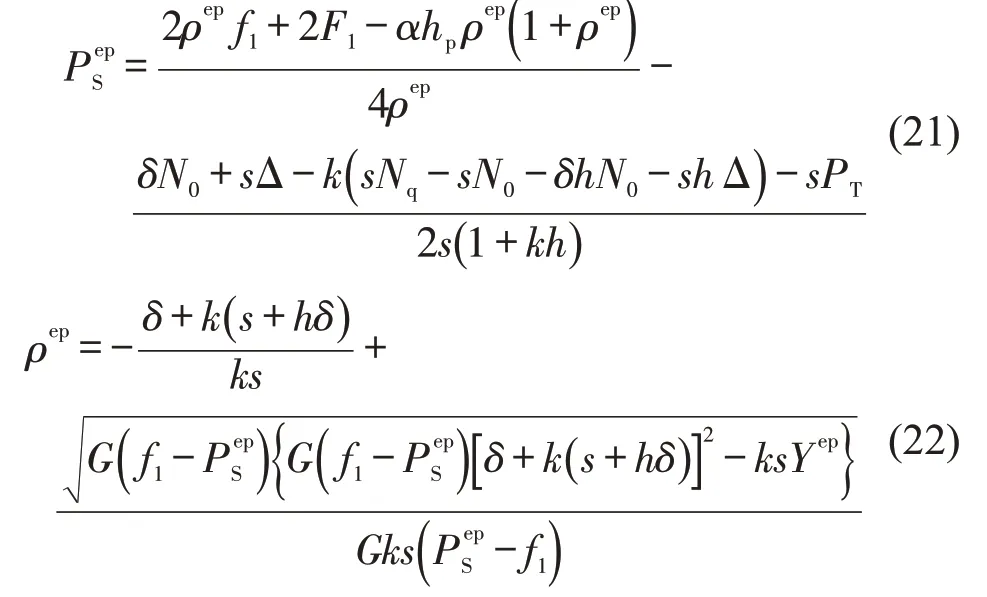
4 算例分析

参数设定如下：N=2 000 人，Nq=3 000 人，h=30，N0=600 人，单位拥挤程度带来的不舒服成本k=0.015，(α,β,γ)=(1.2,0.6,3)元/min，δ=，高速路的通行能力s=40 车/min，接一个乘客的时间hp=1min，私密性成本Δ=2 元，PT=7 元，f1=4 元/人，f2=2 元/人，F1=20 元/车，F2=3 000 元/车.表1为4种情形下的均衡结果.

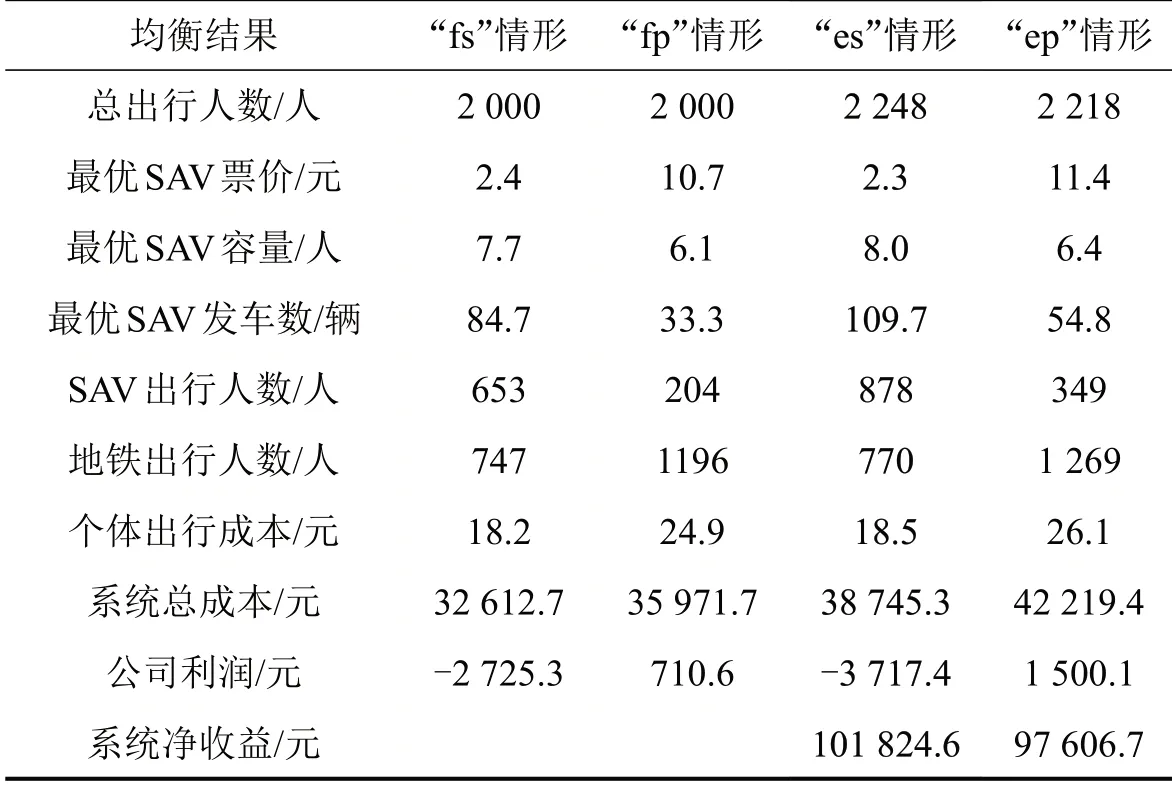
表1 4 种情形下的均衡结果Table 1 Equilibrium results regarding to four cases

由表1 可知：无论是固定需求还是弹性需求，SAV 公司垄断经营均会收取较高的SAV 票价，提供容量较小的SAV 车型，会抑制选择SAV 的出行需求，故最优发车数会相应降低；系统最优情形下，SAV 公司无法获得正利润，需要政府补贴运营，但社会福利效果明显.SAV垄断经营情形下，虽然SAV 公司可以获得正收益，但以牺牲个体出行成本或系统总成本为代价，系统净收益较低(弹性需求下).

图1 为“fs”和“fp”情形下C、l、NS及π随不同PS-ρ的变化情况.并显示了“fs”情形下的最优解(图1(a))和“fp”情形下的最优解(图1(d)).“fs”情形的最优SAV 票价为2.4 元，最优SAV 容量为7.7人，C、l和NS分别为32 612.7元、84.7辆、653 人；“fp”情形的最优SAV 票价为10.7 元，最优SAV 容量为6.1 人，π、l和NS分别为710.6 元、33.3 辆、204 人，与表1 结果一致.对比图1(a)、(d)发现：达到系统最优时，SAV 利润为负，SAV 公司需提供较多的车辆，选择SAV 通勤的人数较多；SAV 公司实现利润最大化时，SAV 公司的发车数量较少，选择SAV 通勤的人数较少，系统总成本较高.

图2为“es”情形下C、l、B及π随不同PS-ρ的变化情况，“es”情形的最优解如图2(c)所示，此时系统净收益最大.“es”情形的最优SAV 票价为2.3 元，最优SAV 容量为8.0 人，此时系统总成本、SAV 发车数、系统净收益和公司利润分别为38 745.3 元、109.7 辆、101 824.6 元、-3 717.4 元.当实现系统净收益最大时，偏离了系统总成本最小点(图2(a)中“□”)和SAV 公司利润最大点(图1(d)中“+”).

图3 为“ep”情形下C、l、B及π随不同PS-ρ的变化情况，“ep”情形的最优解如图3(d)所示，此时公司利润最高.“ep”情形的最优SAV票价为11.4 元，最优SAV 容量为6.4 人，C、l、B、π分别为42 219.4 元、54.8 辆、97 606.7 元、1 500.1 元.C最优解(图3(a)中“□”)和B最优解(图3(c)中“×”)均偏离“ep”情形的最优值，即实现SAV 利润最大化时，会产生较高的系统总成本和较低的系统净收益.

图1 “fs”和“fp”情形下C 、l 、NS 、π 随不同ρ - PS 的变化情况Fig.1 Variation of C,l, NS, π with different ρ-PS under cases of“fs”and“fp”

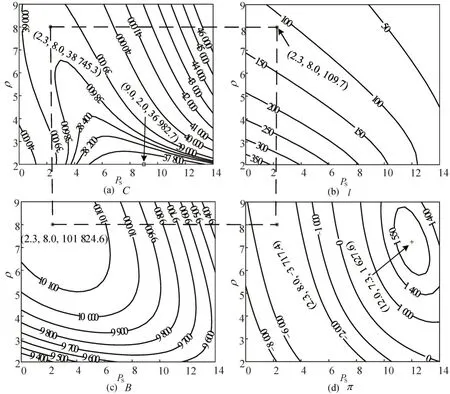
图2 “es”情形下C 、l 、B 、π 随不同ρ - PS 的变化情况Fig.2 Variation of C、l、B、π with different ρ-PS under case of“es”

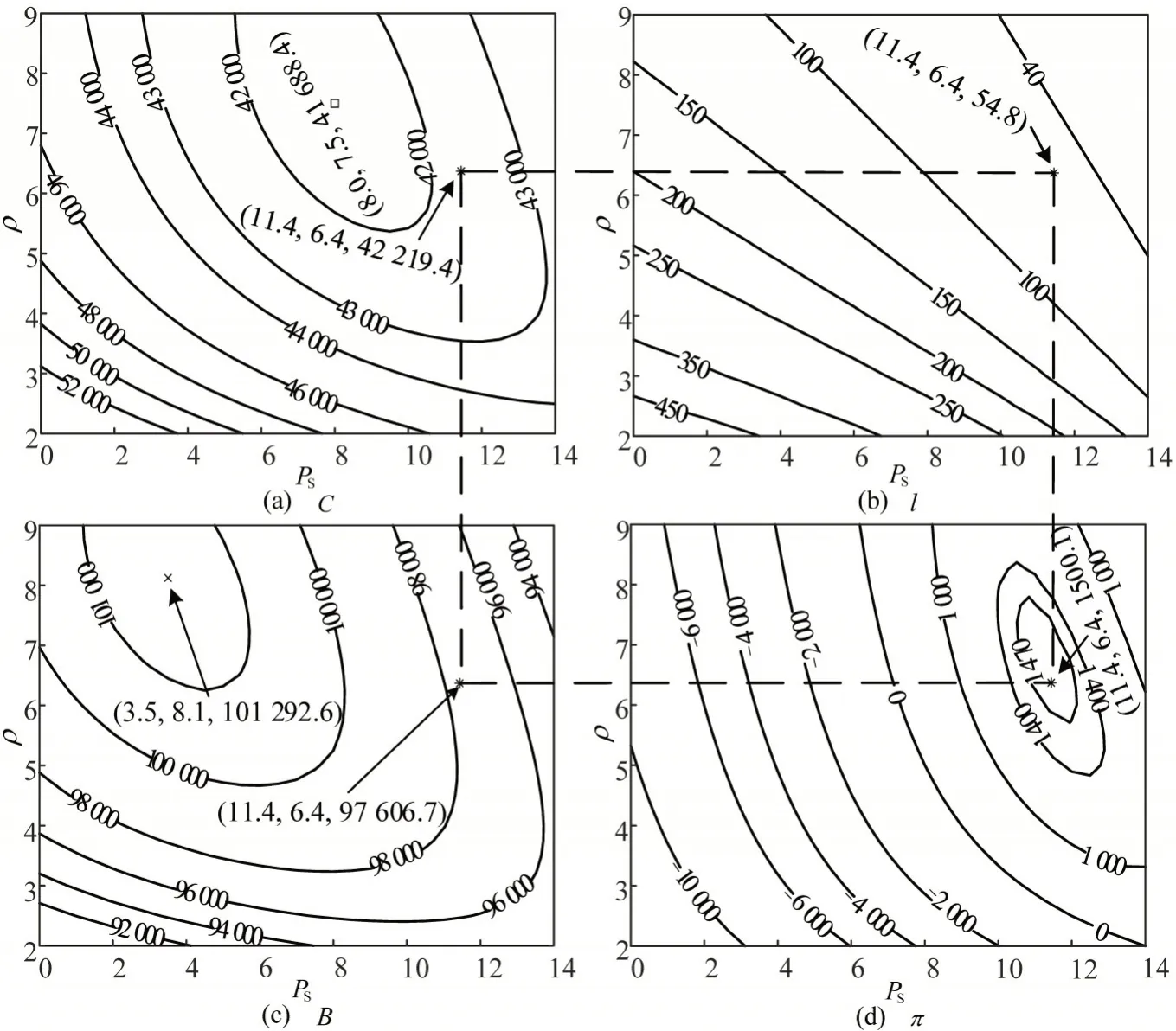
图3 “ep”情形下C 、l 、B 、π 随不同ρ - PS 的变化情况Fig.3 Variation of C、l、B、π with different ρ-PS under case of“ep”

5 结 论

基于经典两模式情景，在SAV 与普通车共存背景下，分析固定需求和弹性需求两种情形，SAV公司在不同经营目标下如何合理选择经营策略的过程，对比4 种情形下的系统总成本、系统净收益(弹性需求下)、SAV 最优发车数量、公司利润等指标，发现SAV公司垄断经营均会收取较高的票价，提供容量较小的SAV 车型，提供较少的运营车辆数量，系统总成本较大.如果SAV公司的运营目标是实现系统总成本最小或净收益最大，则无法获得正收益，需要政府补贴运营，但提供的SAV运营车辆数量较多且容量较大，对应的系统总成本较小.本文是在理想假设条件下开展的，提供一些未来可能场景下关于SAV 公司运营策略的建议，还有很多因素未考虑，如SAV 乘客由于可在车内从事其他活动其单位时间价值将减小，高速路上的不确定性等，这将是下一步的工作方向.