基于深度集成学习的手写数字识别

周燕艳， 范学满， 海 深

(1.铜陵学院 数学与计算机学院，安徽 铜陵 244000；2.海军潜艇学院 作战指挥系，山东 青岛 266199)

手写数字识别是计算机视觉领域的一个重要研究方向。目前，仍有大量的手写数字单据需要录入计算机进行管理，比如物流行业中手写快递单据、银行业的手写支票和汇款单、公司账本等，如果能进行智能化的手写数字识别，则可以节省大量的人力[1]。手写数字识别本质上是一个包含10个类别的分类问题，对应0、1、2、…、9共10个数字。该问题看似简单，但实际识别精度却低于手写汉字识别，主要原因如下[2]：第一，数字笔画简单，笔画差距相对较小，字形相差不大；第二，受地域影响，同一数字的写法风格千差万别；第三，数字间缺乏上下文关联。因此，研究高效率、高精度的手写数字识别算法既具有实际意义又极富挑战性。

手写数字识别是深度学习在图像识别领域的典型应用场景之一。传统的人工提取图像特征方式逐渐被基于深度学习的深层网络学习特征方式所取代。由于深度学习免了对图像的复杂前期预处理，可以直接输入原始图像，因而得到广泛应用[3-4]。将深度学习应用于手写数字识别在一定程度降低了分类错误率[5]，但随着神经网络深度的增加，在模型训练过程中也出现了很多问题，例如过拟合、训练低效、泛化能力弱等[6]。集成学习是将多个具有差异性的弱分类器联合起来，通过优势互补来提高集成分类性能，从而将弱分类器提升为强分类器[7]。目前，集成学习在语音信号处理、病症检测、时间序列预测等方面都有一定的应用研究[8]。集成方法的核心就是通过降低个体复杂度，增加群体差异性，来提高集成分类器的预测性能，这为改善深度学习的泛化能力和过拟合问题提供了新的思路。

本文将集成深度学习用于手写数字识别领域，以经典的多层感知器(Multi-layer Perceptron，MLP)作为基分类算法，训练出多个具有差异性的基分类器，以自适应增强算法(AdaBoost)[9]作为集成策略，构成集成深度学习模型——自适应增强多层感知器(Adaptive Boosting Multi-layer Perceptron，AdaBMLP)。基于MNIST手写数据集寻优确定AdaBMLP的参数，进行交叉校验实验验证模型的有效性。

1 集成学习有效性分析

2000年，Ditterich[10]将集成学习、符号学习、统计学习、强化学习列为21世纪机器学习领域的4个主要发展方向，其中集成学习位居第一位。集成学习的有效性可以从内部条件和外部原因两方面进行分析。

1.1 有效性的内部条件

集成学习中常用的输出融合算法包括多数投票、加权投票、模糊积分、概率估计、D-S证据理论等。其中，多数投票是最简单而且较为有效的集成方法。这里以多数投票法为代表，分析有效性的内部条件。

设共有L个基分类器(L为奇数)，第i个基分类器Ci的类别输出用M维二值向量表示，即[di,1,di,2,…,di,M]∈{0,1}M，i=1、2、…、L，M为分类问题的类别数，di,j=1表示分类器Ci将样本x分为ωj类，则多数投票法的分类决策为

(1)

设每个基分类器对于任意样本x∈Rn，正确分类的概率为p，且各基分类器的输出结果相互独立，即对任意基分类器子集A={C(1),C(2),…,C(K)}⊆C，联合概率决策函数满足

P(C(1)=l1,…,C(K)=lK)=P(C(1)=l1)×…×P(C(K)=lK)，

(2)

式中lK为基分类器C(K)的类别输出。

为简化问题而又不失一般性，对于二分类问题(M=2)，由式(1)可知，集成分类器分类正确的充要条件是至少⎣L/2」+1个基分类器分类正确，集成分类精度为

(3)

⎣」代表向下取整，由式(3)可以得出以下结论：

(1)当p>0.5时，Pmaj随L单调递增，且有

(4)

(2)当p<0.5时，Pmaj随L单调递减，且有

(5)

(3)当p=0.5时，∀L，Pmaj=0.5。

综上所述，从集成学习内部来看，对于二分类问题，基分类器的独立分类正确率p应大于0.5才能保证集成学习的有效性；推广到多分类问题(M>2)，则需要满足p>1/M，即基分类器的性能应优于随机猜测。

1.2 有效性的外部原因

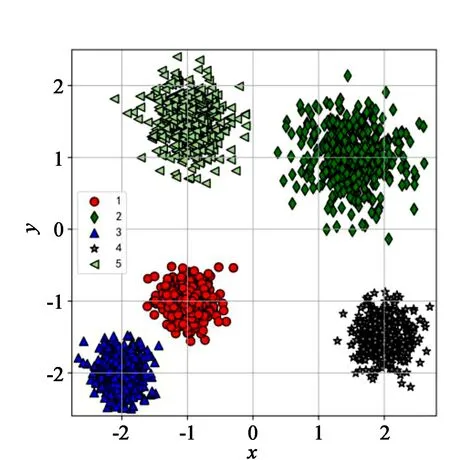
图1 自制数据集

在1.1节中分析集成学习有效性的内部条件时，某些假设条件过于理想化，在实际使用中可能无法满足，如要求基分类器的类别输出相互独立。即便如此，分类器集成在精度、鲁棒性和泛化能力方面的优势依然显著，这促使业界分析其有效性的外部原因。目前学者们就分类器集成有效性的外部原因，在统计、计算和表示3个层面上达成了共识[11]。

1.3 MLP的不稳定性分析

为了保证集成学习的有效性，还有一个隐含条件，即基分类算法必须具有不稳定性，这样才能保证生成的基分类器集合具有多样性。下面基于自制数据集来分析MLP是否满足不稳定性要求。选取的5个正态分布的均值分别为(-1,-1)、(1.5,1)、(-2,-2)、(2,-1.5)、(-1,1.5)，标准差分别为0.2、0.4、0.2、0.25、0.3，随机生成了2000个样本点，如图1所示。

使用Scikit-learn机器学习库中的MLP模型，基于上述数据集进行4折交叉验证实验。实验中MLP使用修正线性单元作为激活函数，采用随机梯度下降的优化器，其余参数取默认值。进行4折交叉验证后，我们把得到的4个MLP的决策边界绘制出来，如图2所示。

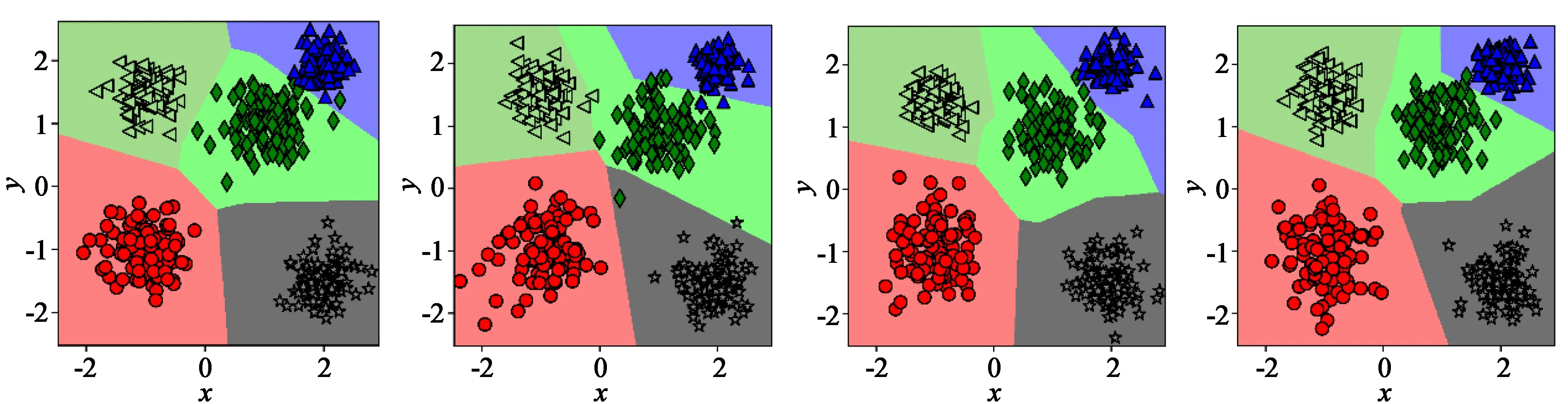
(a)第一个MLP (b)第二个MLP (c)第三个MLP (d)第四个MLP

图2中基于不同训练子集生成的MLP的分类边界有明显差异，表明MLP具有不稳定性，可以用作集成深度学习的基分类算法。

2 AdaBMLP手写数字识别算法

AdaBMLP是深度学习算法MLP与集成学习算法AdaBoost的联合。如图3所示，AdaBMLP在用于手写数字识别时遵循两个阶段，首先是基于训练集生成具有差异性的多个基分类器；然后利用AdaBoost联合各基分类器的输出，得到最终的识别结果。

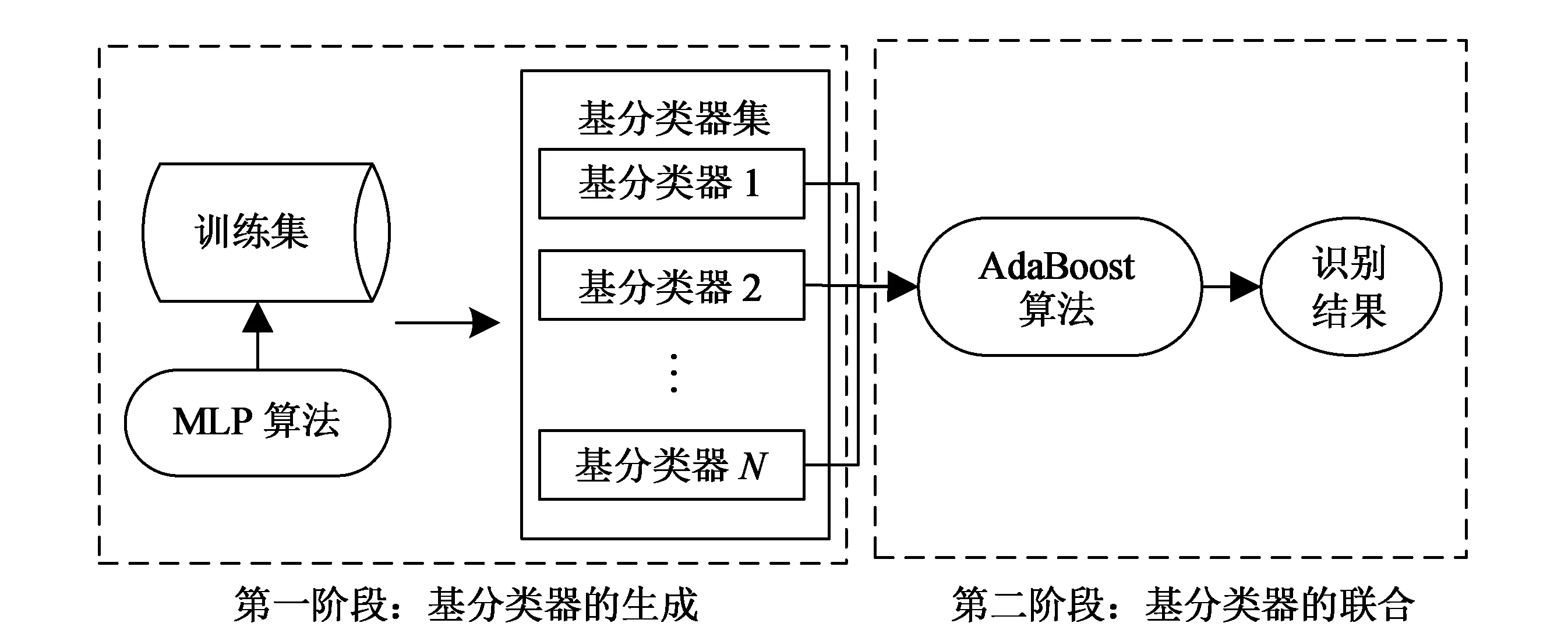
图3 AdaBMLP的一般流程

2.1 MLP算法

MLP是最典型的深度学习模型之一，由一个输入层、一个输出层和多个隐含层组成，相邻两层的所有神经元两两相连，且网络中不存在回路[12]，如图4所示。

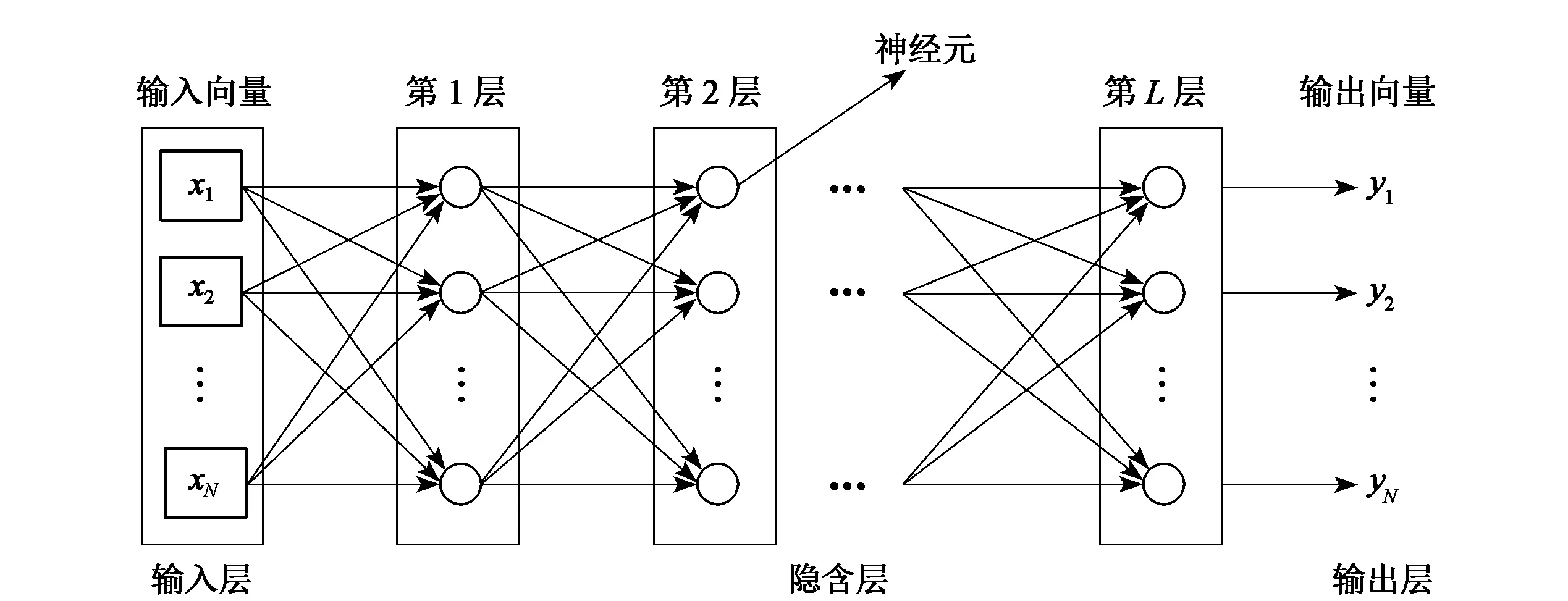
图4 MLP的结构示意图

2.2 AdaBoost集成

如图5所示，AdaBoost集成可以分为3步：首先，初始化样本集权重；然后，自适应训练多个弱分类器；最后，将多个弱分类器集成为强分类器。

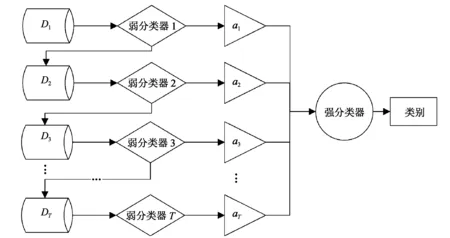
图5 AdaBoost示意图

具体步骤如下[13]：

(1)初始化训练数据的权重分布，此时

D1=(w1,1,w1,2,…,w1,N0,w1,N0+1,…,w1,N)，

(6)

通常根据样本所属类别的比例来初始化样本的权重。

(2)进行迭代t=1,2,…,T。

①利用权重分布为Dt的样本集，训练得到弱分类器ht，并基于权重分布为Dt的样本集，计算ht的再代入分类错误率et：

(7)

式中ht(xi)为ht在样本xi的预测类标签，yt为样本xi的真实类标签，wt,i为第t次迭代时第i个样本的权重。

②计算ht在最终集成分类器中所占权重at：

(8)

③更新训练样本集的权重分布Dt+1：

(9)

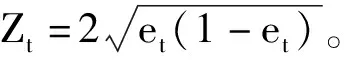
(3)将T个弱分类器按照权重at集成为一个强分类器：

(10)

式中sign(·)为符号函数。

3 实验

基于MNIST手写数据集进行识别实验。首先，寻优确定MLP的主要参数；然后，在此基础上进一步确定用于Adaboost集成的基分类器的数目。实验在Spyder集成开发环境中，基于Sklearn机器学习库，利用Python编程实现[14]。

3.1 MNIST手写数据集

MNIST手写数据集是由Google实验室、纽约柯朗研究所及微软研究院整理的不同年龄段人群的手写数字构成的集合。MNIST数据集中包含60 000个训练样本和10 000个测试样本组成，每张图片有28×28个像素点构成，每个像素点用一个灰度值表示，部分手写数字图片如图6所示。可以看出手写数字的字体、风格因人而异，这给正确识别增加了一定困难。

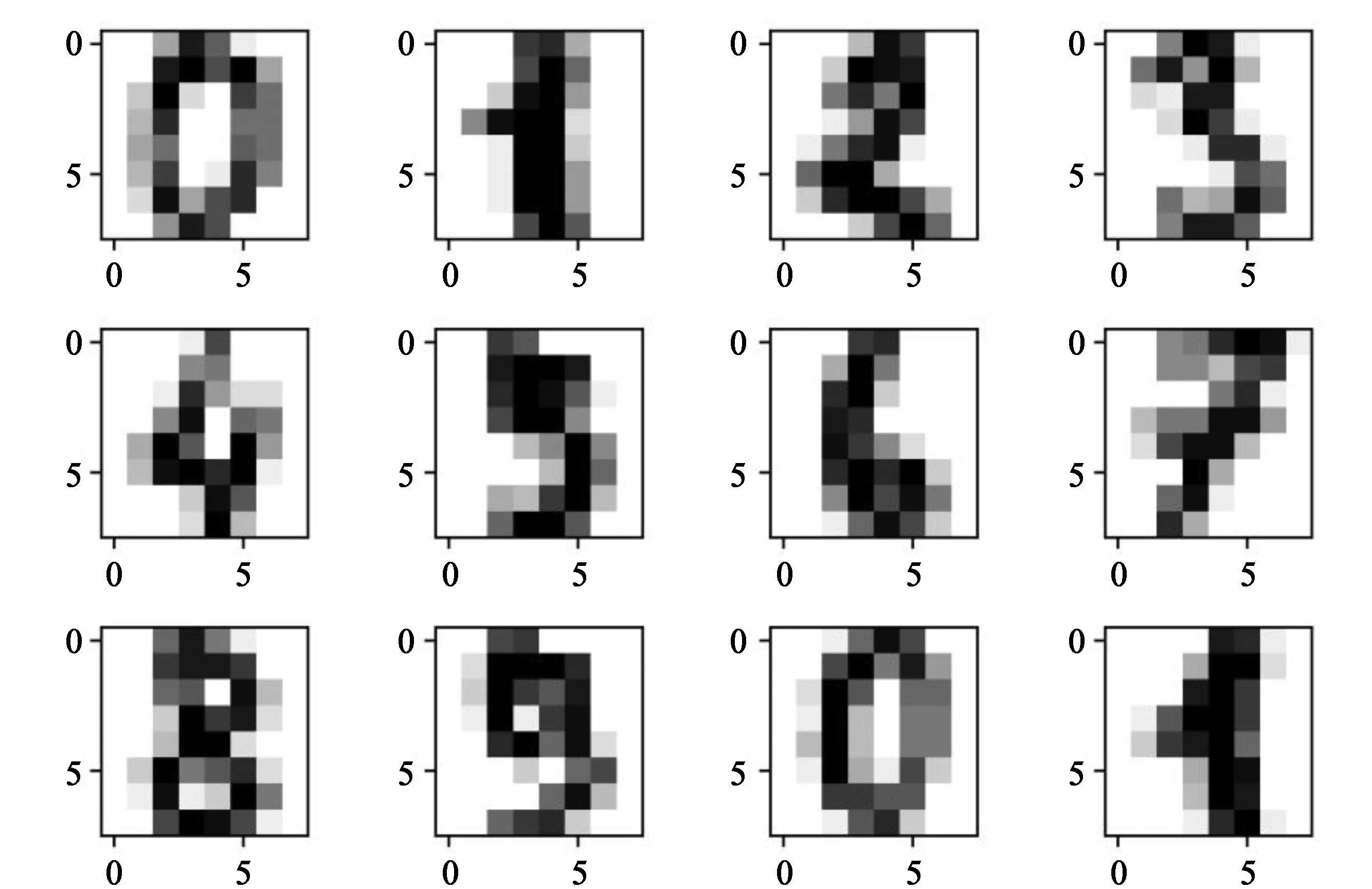
图6 手写数字图片

3.2 MLP参数寻优

MLP的主要参数包括隐含层的层数、隐含层的单元数、激活函数的类型以及迭代次数，需要说明的是迭代次数是指每个训练样本所使用的次数，而非梯度下降的步数。为了降低过拟合风险，本文设置隐含层数为1，迭代次数为50，重点对隐含层单元数和激活函数种类进行寻优。

实验过程中，隐含层单元数取值从1到59，间隔为2，共30种情况；激活函数选取identity、logistic、tanh和relu函数，共4种情况。综上所述，总共有120种参数设置情况。对于每种情况，进行5折交叉验证实验，计算平均识别正确率作为评价对应参数配置好坏的标准。所得结果如表1所示，每种激活函数对应的最高识别正确率已在表格中加粗显示。

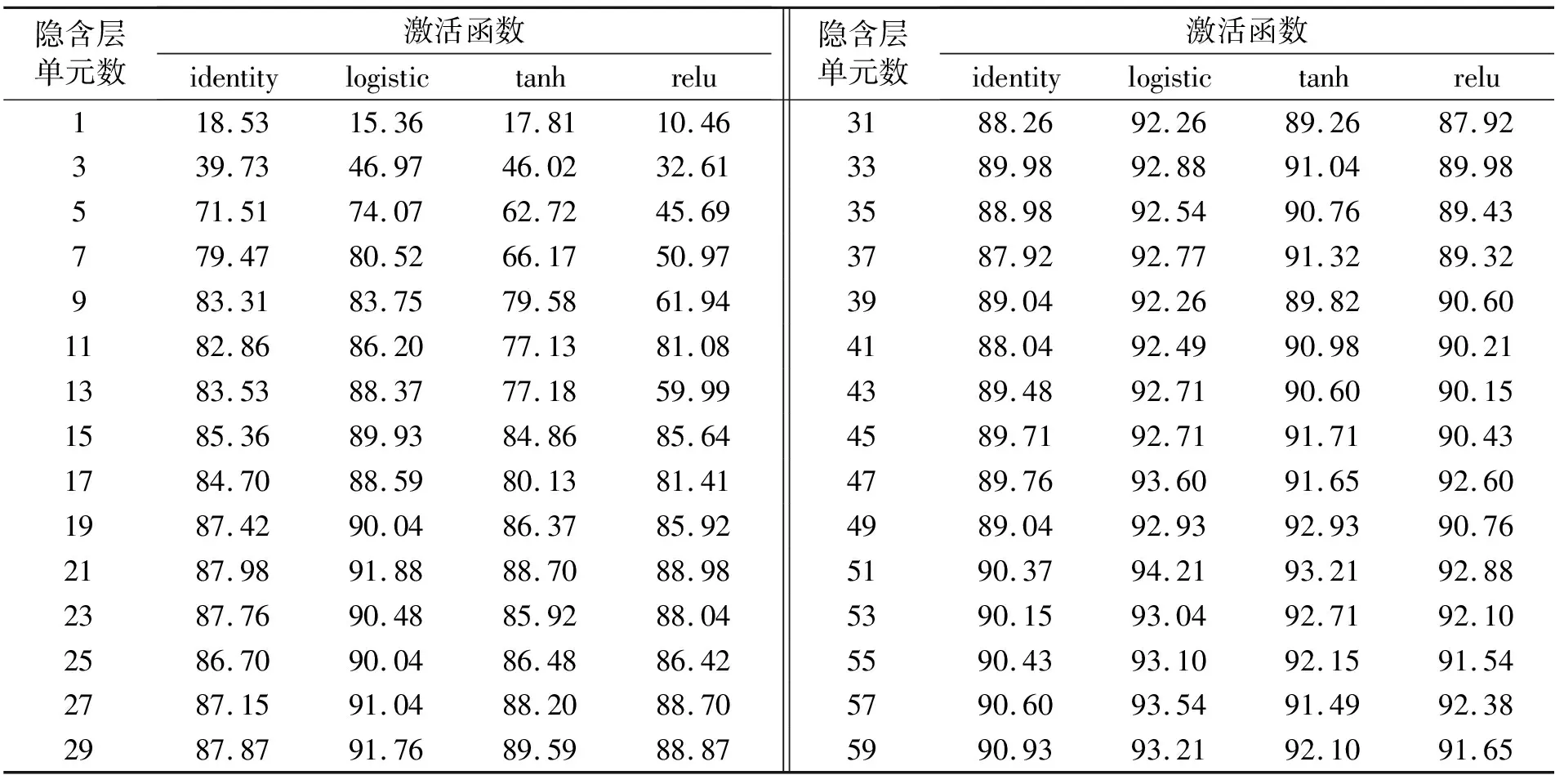
表1 不同参数配置识别正确率 %

由表1可知，在隐含层单元数一定时，使用logistic作为激活函数，识别正确率明显高于另外3种激活函数，因此我们将MLP的激活函数确定为logistic。对于logistic激活函数，当隐含层单元数为51时，识别正确率取得最大值。综上所述，我们将MLP的参数设置为：logistic激活函数和51个隐含单元。

3.3 集成深度学习的基分类器数目

AdaBMLP的基分类器个数取决于AdaBoost的迭代次数T，基于MNIST手写数字集进行5折交叉校验，研究训练精度和测试精度随迭代次数T的变化。具体操作是，将原始数据集随机分为等大的5份，轮流将其中1份作为测试集，其余4份作为训练集，每轮得到一组训练精度和测试精度，取5次预测结果的均值作为模型预测效果的估值。实验结果如图7所示。

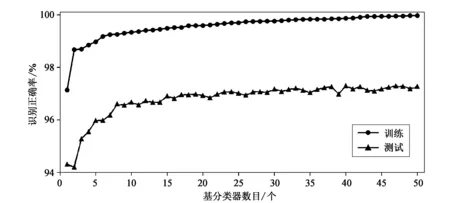
图7 基分类器数目对识别正确率的影响

由图7可见，随着迭代次数即基分类器个数的增加，AdaBMLP在训练集和测试集上的识别正确率，总体上都呈现出先迅速上升后趋于稳定的变化趋势。当基分类器个数达到40个时，AdaBMLP在训练集上的识别正确率已接近100%，且基本稳定；AdaBMLP在测试集上的识别正确率也不再有明显变化，上下稍有波动趋于稳定。综合考虑集成模型在测试集和训练集上的识别性能，建议将AdaBoost的迭代次数设置为40，即AdaBMLP由40个MLP集成得到。

4 结束语

为了缓解手写数字识别精度受书写风格影响较大的问题，本文将集成学习与深度学习相结合，以MLP作为基分类算法，以AdaBoost作为集成算法，构建集成深度手写数字识别模型AdaBMLP。基于MNIST手写数字集进行寻优实验，确定了AdaBMLP的主要参数：MLP采用logistic作为激活函数，隐含层单元取51个，基分类器数目为40个。另外，实验表明通过集成可以比单独使用MLP获得更高的识别正确率。

本文研究只是初步验证了集成深度学习在提升手写数字识别效果方面的可行性，在深度学习算法方面选取了比较经典的前馈全连接神经网络，后续将研究集成学习与卷积神经网络(convolutional neural network，CNN)、循环神经网络(recurrent neural network，RNN)以及对抗生成网络(generative adversarial network，GAN)等新型网络结构联合，进一步提升手写数字识别的泛化能力和对噪声的鲁棒性。