三维切削力测力仪结构的多目标优化设计

赵瑞杰， 王 鹏,2,3*， 王 楠,2,3， 杜宇波， 黄珂卿

(1.陕西理工大学 机械工程学院，陕西 汉中 723000；2.陕西省工业自动化重点实验室，陕西 汉中 723000；3.陕西理工大学 机电设备智能监测与控制研究所，陕西 汉中 723000)

制造业是一个国家经济发展的基础，在全球化智能制造大环境的推动下，高档数控机床作为先进制造业中的机械加工智能装备，被列入“中国制造2025”十大重点发展领域[1-2]。高档数控机床的智能化发展必须开发智能监测技术[3]，在金属切削过程中，刀具与工件接触，发生相对移动并产生切削力，切削力是评价刀具性能指标的重要依据，精确测量切削力，研制高性能的车削力测力仪能够实现对数控机床切削状态的智能监测[4]，使加工零件获得更高的精度，并能提高生产效率。多年来国内外学者在切削机理和测量原理方面不断地深入研究，应变式切削力测力仪因可靠性高、成本低、适用范围广等特点获得了广泛的应用[5]。而应变式车削力测力仪也有本身不可避免的一个弊端，即无法兼具高固有频率和高灵敏度[6]。韩丽丽[7]在有限元分析的基础上，运用ANSYS优化程序对无定心钻削测力仪进行了结构优化，试验检测后的测力仪在各种性能上达到实际应用标准，且减小了测力仪的体积；王娟等[8]运用ANSYS对剪切刚度和拉压灵敏度进行综合优化，得到了弹性敏感结构的理想结构参数；王明强等[9]利用多目标拓扑优化方法，以固有频率最大和弹性体特定位置应力集中为优化目标，实现了对高速微切削应变式测力仪弹性体的优化设计，减小了测力仪的质量；赵友等[10]设计了一种基于正交八角环式的车削力测力仪，该结构设计实现了三维力的解耦测量，提高了弹性体结构的固有频率，但并没有同时提高弹性敏感结构的灵敏度。

本研究在正交八角环的基础上提出了正交十角环敏感结构，根据尺寸参数对结构灵敏度和刚度的影响程度[5]，建立参数化模型，以十角环结构变形最大、主切削力方向固有频率最大为优化目标，采用响应面多目标优化方法对模型结构参数进行优化分析。

1 正交十角环结构及工作原理

1.1 正交十角环结构

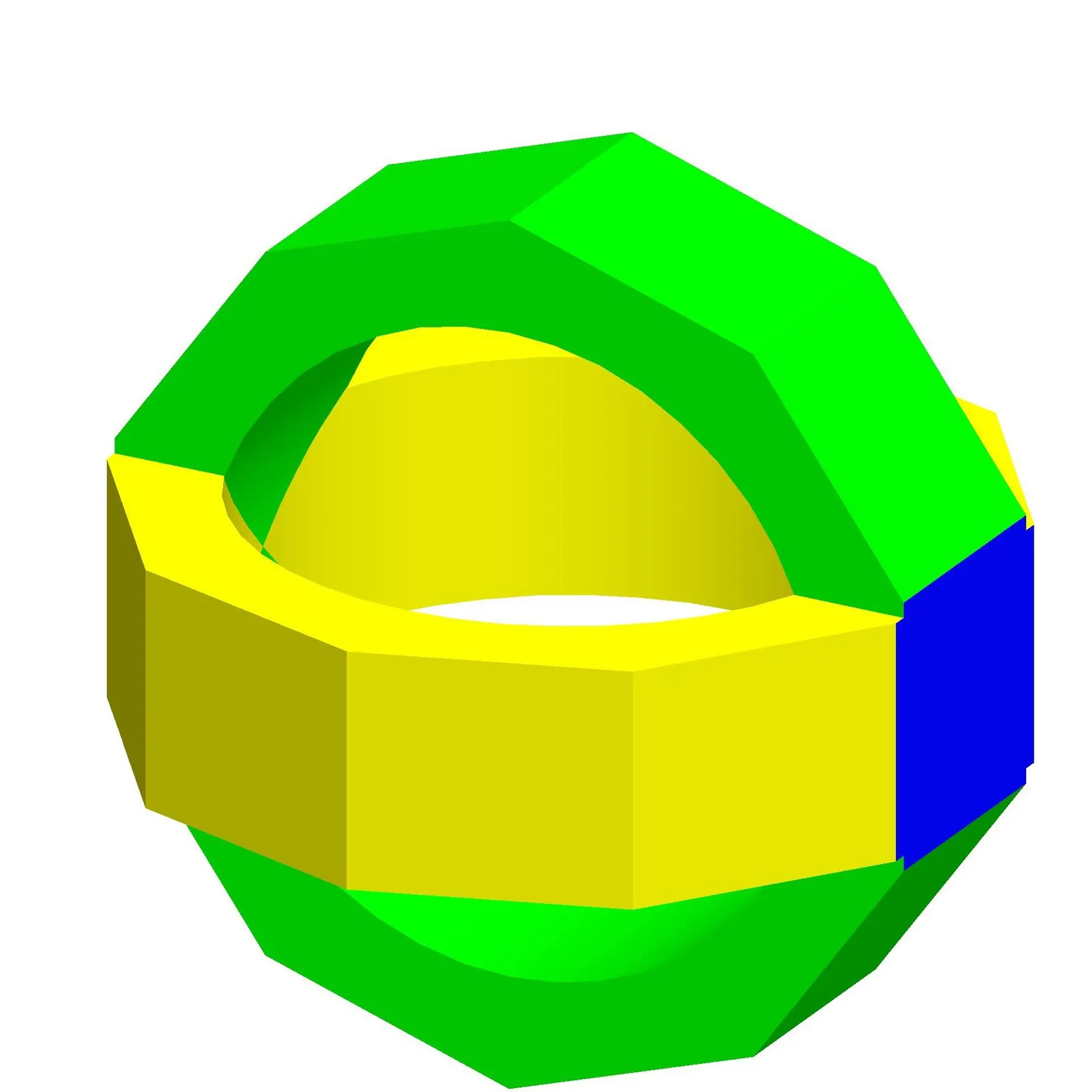
图1 正交十角环结构

在测力仪弹性敏感元件模型设计阶段，综合考虑测量灵敏度、结构刚度、结构稳定性和可加工性等因素的影响，本文对测力仪原有的正交八角环结构进行改进设计，提出了一种正交十角环弹性敏感结构。如图1所示，该结构是由一整块棒料经过车削、线切割、磨削等加工工艺加工而成[5]，两个十角环相互垂直，中间为空心结构，水平十角环与竖直十角环尺寸大小一致，十角环的内径、厚度、宽度分别为51、9、15 mm，该设计将三维切削力分解到两个互相垂直的平面内，可以减小测量时三维切削力之间的交叉干扰。

传统八角环结构的使用是受到了圆环弹性结构的启发，对其进行受力分析也是按圆环模型进行了理论推导[6]，而十角环结构更接近于圆环，计算更加准确；且在满足一定刚度要求的情况下，其十角环结构的灵敏度更大一些。

1.2 工作原理

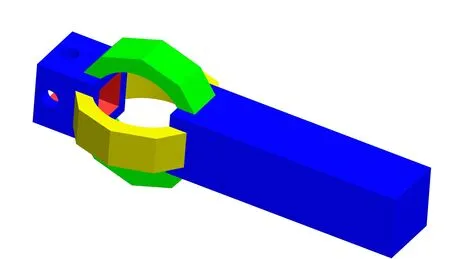
图2 正交十角环式测力仪结构模型

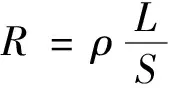
2 双正交十角环的有限元分析

通过对测力仪工作原理的分析，在材料线性范围内，正交十角环敏感结构在固定载荷下的变形量越大，越容易被应变片感知，正交十角环测力仪灵敏度越高；且工件在实际加工过程中，测力仪在切削力的作用下会产生振动，为避免引起结构共振，影响测量精度，结构的固有频率要远大于主轴旋转的频率[12]，因此对正交十角环敏感结构进行静力学和模态分析是必不可少的环节。

本文运用Design Modeler模块，根据测力仪实际应用尺寸建立有限元三维模型，定义材料属性并施加载荷与约束，分别进行静力学分析与模态分析，具体内容如下。

2.1 材料属性

表1 材料属性

本文定义结构整体采用17-4PH不锈钢材料，具体材料属性如表1所示。

2.2 网格划分

网格划分是有限元分析不可缺少的环节，网格的质量决定了有限元分析的精确度和速度，对后续优化实验设计有着至关重要的作用。目前有限元分析中使用较多的网格类型有四面体、六面体和二者混合单元，四面体网格划分不适用于薄实体或环实体，六面体网格划分变形性好、精度高。为了更加接近本研究的实体模型，本文采用六面体主导划分方法，定义平均单元边长为0.60 mm，划分后的结构模型得到了37 793个节点，139 966个单元，如图3所示。

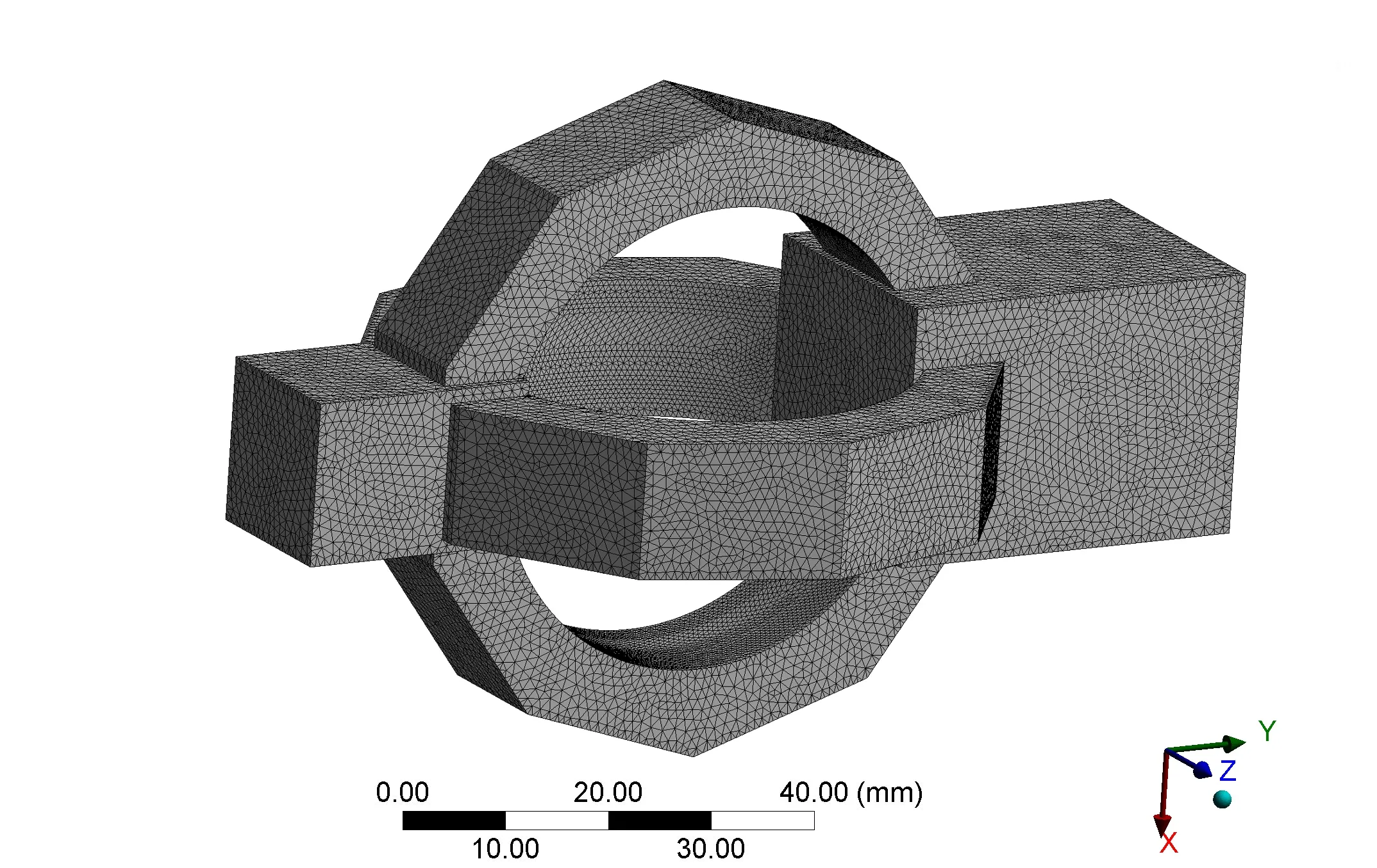
图3 三维模型网格划分图

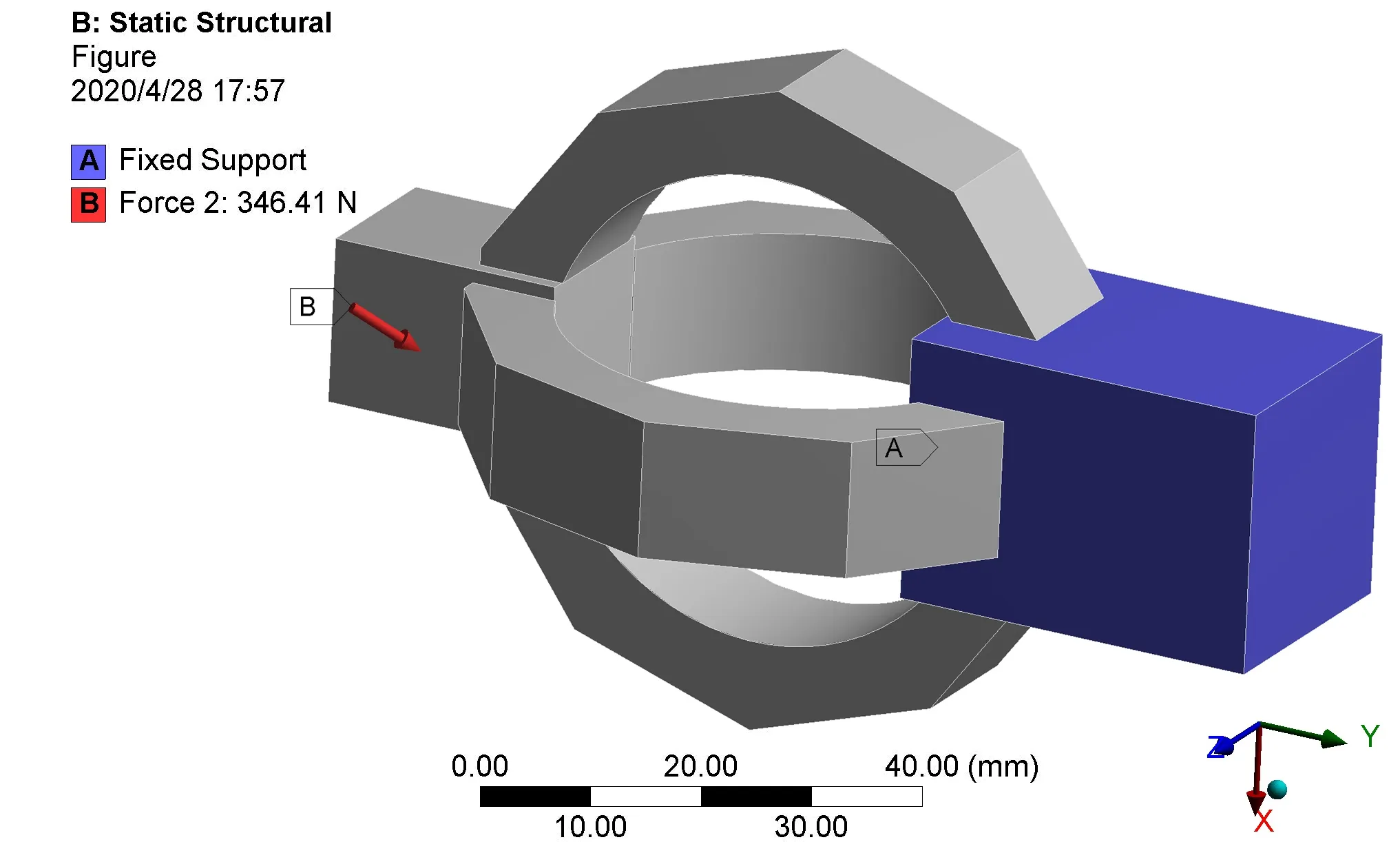
图4 施加载荷与约束

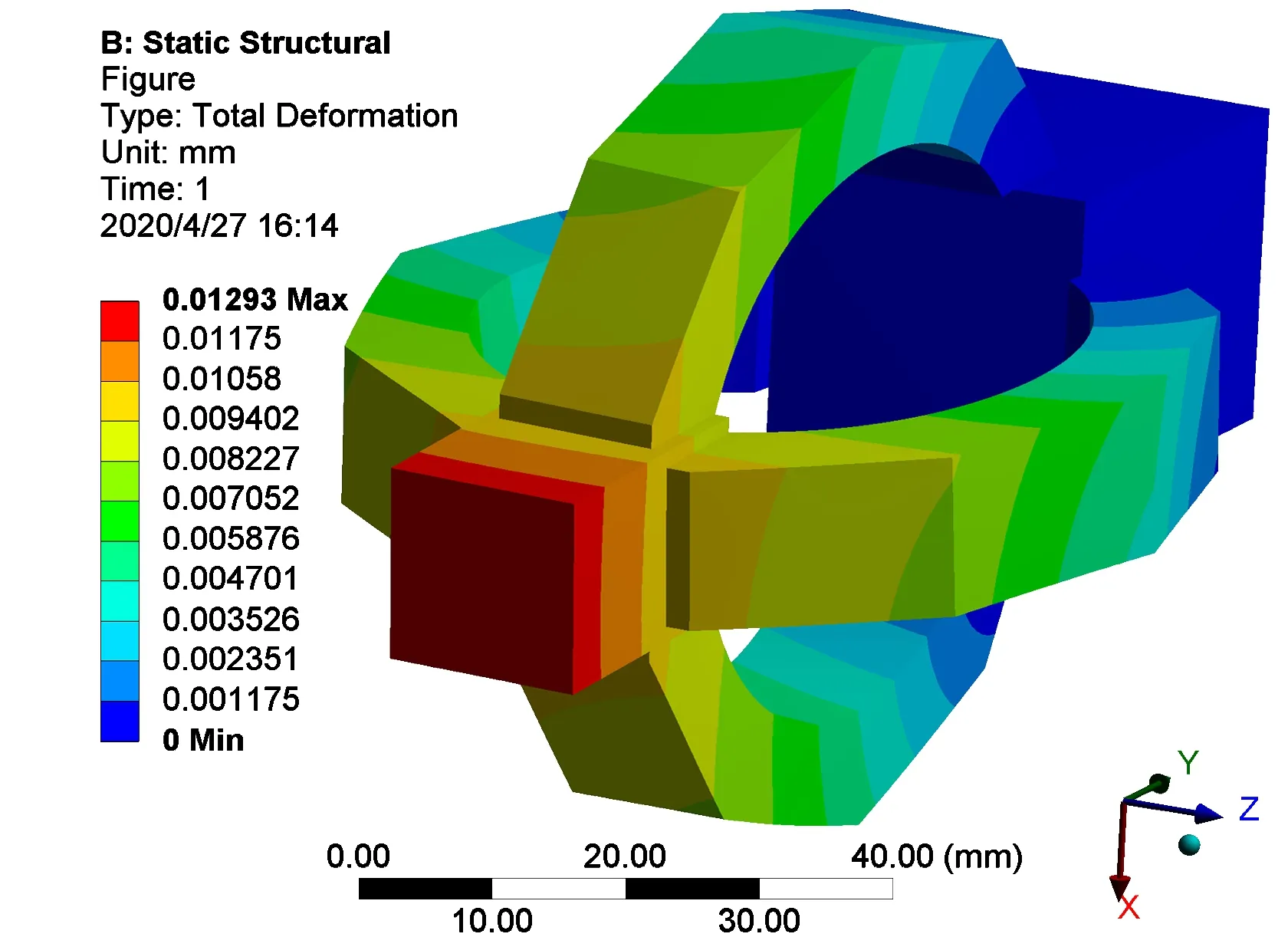
图5 正交十角环变形云图

2.3 施加约束与载荷

精加工和半精加工过程中，主轴转速较高，切削温度升高，摩擦因数减小，剪切角增大，工件与车刀之间产生的切削力较小，一般在百牛顿左右。本文拟施加200 N的力分别作用于主切削力Fx、吃刀抗力Fy、进给力Fz三个方向上；结合实际安装环境，将测力仪后端条形长柄的6个面设置为固定约束面，如图4所示。

2.4 结果分析

图5为正交十角环变形云图。由图可知，正交十角环结构在三维切削力的作用下，应力集中分布在车刀插槽与十角环、十角环与尾部条形长柄的连接处，产生的最大变形量为0.012 93 mm，在材料属性、网格划分方法、载荷大小和固定约束相同的情况下，本文研究对象变形量比改进之前的八角环结构变形量大0.001 712 mm，因此十角环结构比八角环结构拥有更高的灵敏度。

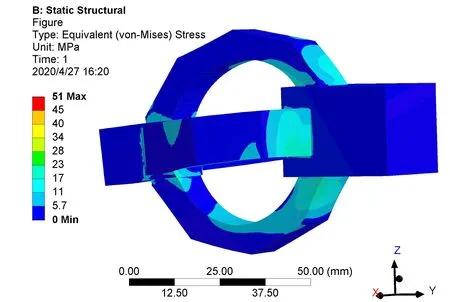
图6 正交十角环表面应力云图

图6为正交十角环表面应力云图。由图可知，十角环结构产生的最大应力为51 MPa，结构在满量程测量范围内产生的最大应力远远小于材料的许用应力，说明改进后的弹性敏感结构满足刚度要求，该设计安全可靠。

此外，本文对正交十角环结构进行了模态分析，获得了简化模型的前四阶固有频率，如表2所示。其中第2阶振型为正交十角环整体在ZOX平面上下振动，与主切削力方向相同。

表2 简化模型固有频率

正交十角环式测力仪安装于精加工和半精加工机床，机床主轴转速设定为10 000 rpm，由表2可知，正交十角环弹性结构的二阶固有频率远大于主轴旋转频率，在复杂加工环境下测力仪的的动态性能符合设计要求。

3 优化实验设计

响应面法的多目标优化方法综合了数学、统计学和计算机科学，是一种能有效解决实际工程问题的优化方法。该方法首先在有限元分析的基础上获得大量的实验数据，运用最小二乘法对数据进行拟合，建立响应面数学模型，最后通过多目标遗传算法进行求解并筛选，获得最优解[13-15]。得到优化变量与优化目标之间的函数关系为

(1)

式中y为优化目标，X=(x1,x2,…,xi,…,xn)为优化变量，β为方程的回归系数。

3.1 选取优化参数

由文献[5]可知，十角环内径、厚度、宽度是影响结构性能的3个重要因素，因此本文取十角环内径、厚度和宽度3个重要参数作为优化变量。因十角环表面应变较大位置需粘贴半导体应变计，故结构尺寸不能太小，本文给定了优化变量的边界条件；针对该结构的灵敏度与固有频率是一对相互矛盾的参数，在保证结构满足强度和刚度要求的前提下，优化过程中两者必须同时兼顾，才能提高结构的整体性能。本文选取结构最大变形量和最大二阶固有频率作为优化目标参数，以传统八角环结构最大变形量和最大二阶固有频率作为约束条件，具体多目标优化设计参数如表3所示。

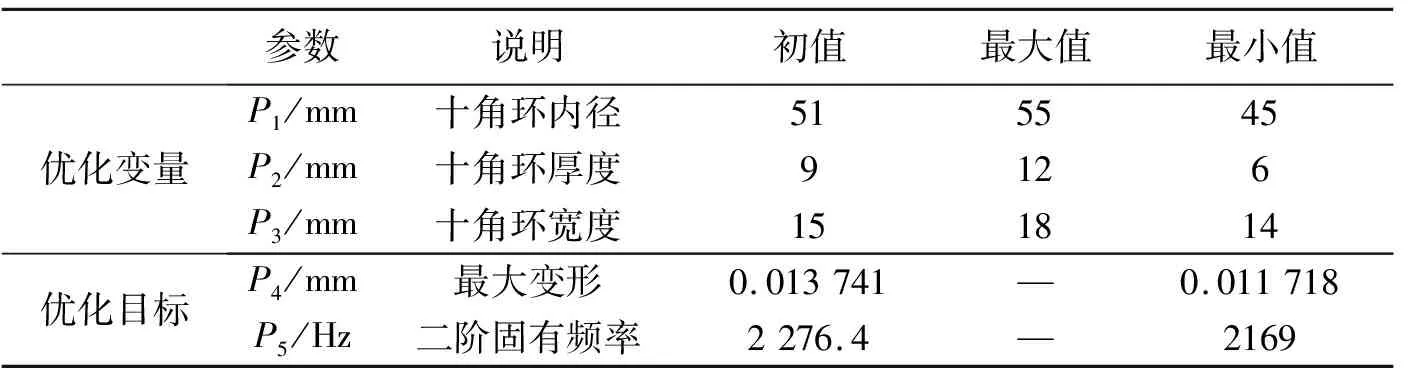
表3 优化设计参数

3.2 实验设计

根据选定的优化变量和优化目标参数，采用中心复合实验方法设计实验，生成如表4所示的样本点。

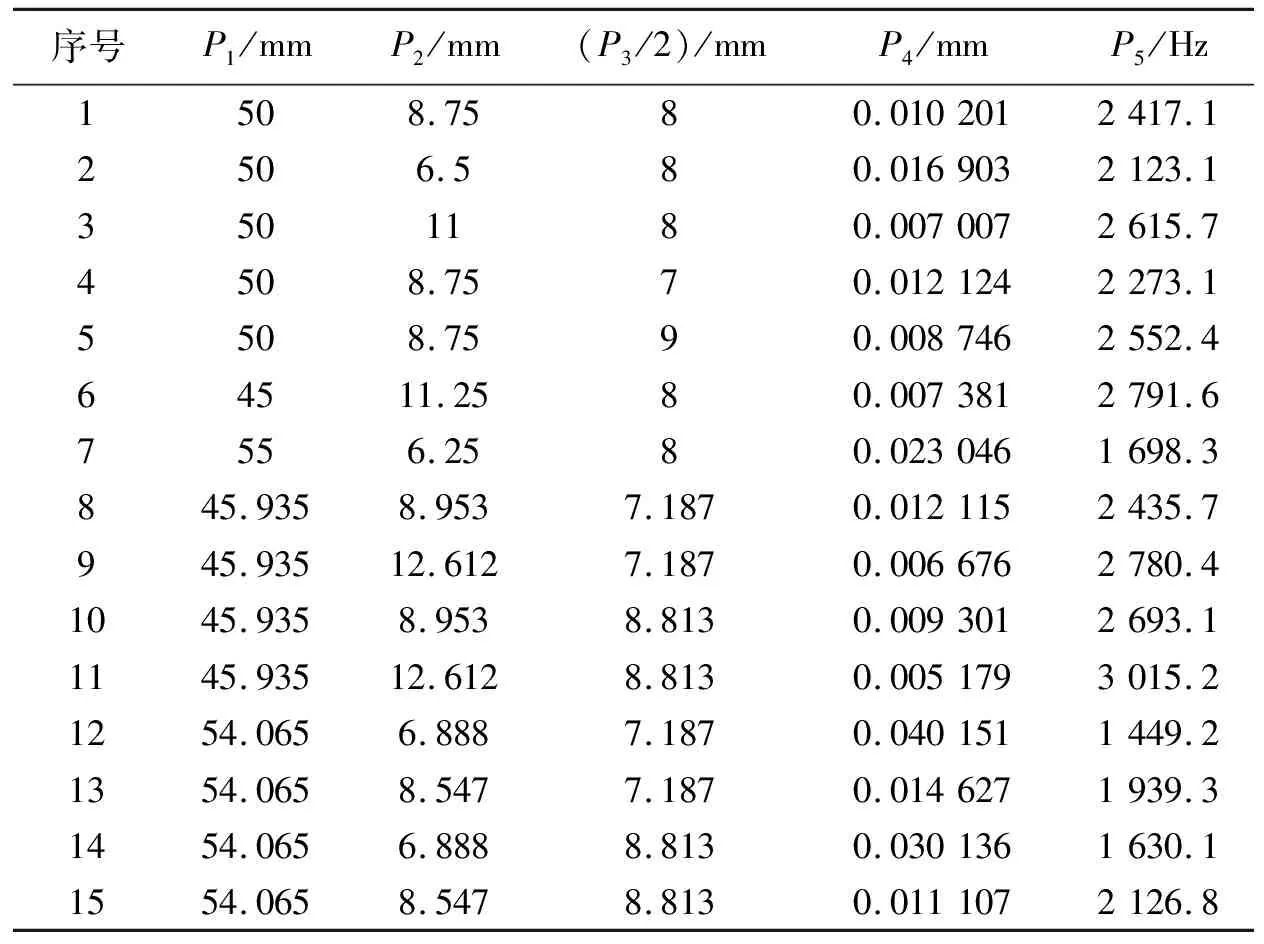
表4 实验设计表

3.3 参数灵敏度分析

依据优化变量与优化目标参数之间的函数关系，在优化设计中通过数学计算获得各变量对最大变形、二阶固有频率的影响灵敏度，该灵敏度值可以很好地指导优化设计过程。图7、图8所示为十角环结构3个优化变量对最大变形、二阶固有频率的灵敏度分析结果。

从图7可以看出十角环内径与十角环结构最大变形呈正相关性，十角环厚度、宽度与十角环结构最大变形呈负相关性，对最大变形依赖性最大的变量是十角环的厚度。由图8可以看出十角环厚度、宽度与结构二阶固有频率成正相关性，而十角环内径则与十角环二阶固有频率呈负相关性，其中十角环内径对二阶固有频率的影响最大，其次是十角环的厚度，十角环的宽度对二阶固有频率的影响相对较小。由图7和图8也可验证固有频率与灵敏度是相互矛盾的这一结论，说明该实验设计是合理有效的。

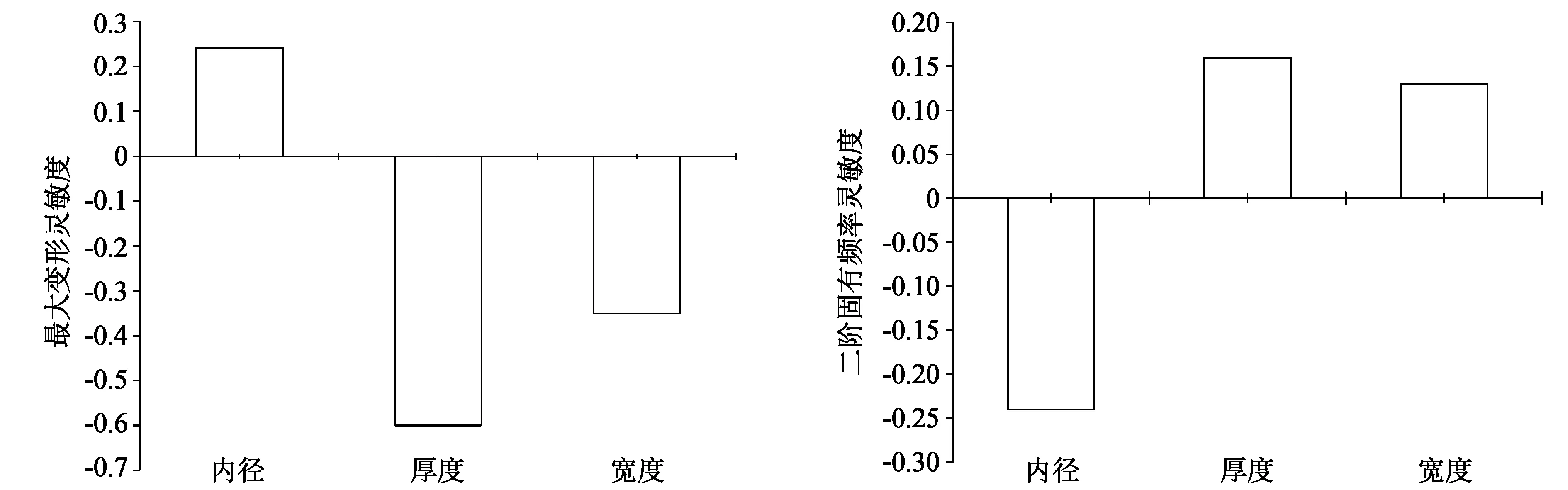
图7 十角环最大变形的灵敏度分析结果 图8 十角环二阶固有频率的灵敏度分析结果

3.4 响应面分析

响应面法实质上是对实验数据运用最小二乘法进行数据拟合，结合统计学原理，获得结构优化变量与优化目标的近似函数表达式，建立2D或3D可视化响应面模型。本文采用CCD实验设计方法建立的响应面模型如图9所示。

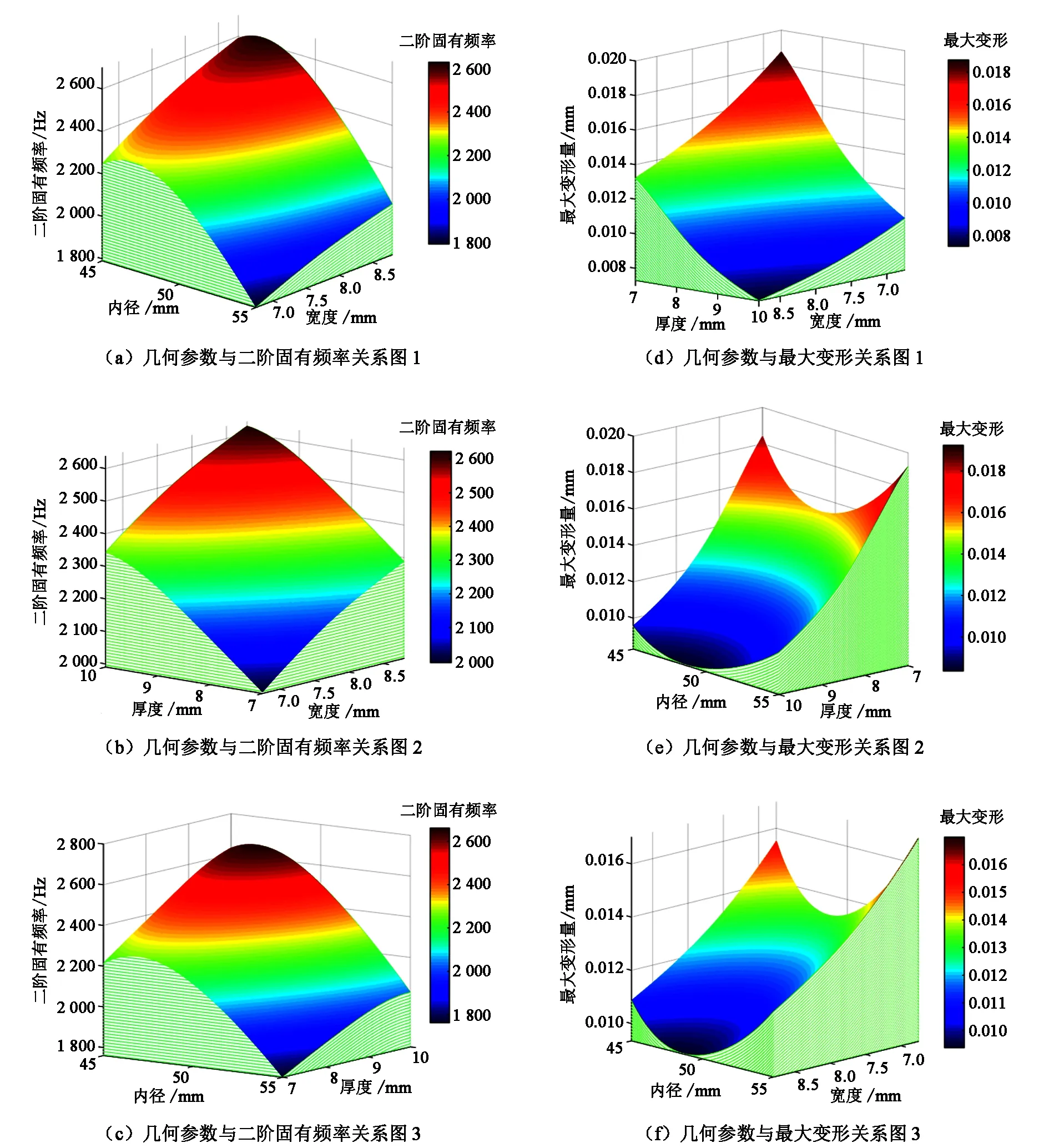
图9 响应面模型

由图9(a)—(c)可知，3个优化变量之间的交互作用中，十角环厚度P1、宽度P2的交互作用对结构二阶固有频率P5的影响最大，且随着十角环内径P1的减小、厚度P2的增大、宽度P3的增大，十角环二阶固有频率P5逐渐增大。由图9(d)—(f)可知，十角环内径P1、宽度P3的交互作用对结构的最大变形P4的影响最小，随着十角环厚度P2、宽度P3的减小，十角环结构最大变形P4逐渐增大，十角环内径P1为49 mm时，结构的最大变形P4是最小的。由响应面分析结论可以看出，有限元分析结果与理论推导非常接近[5]，说明该响应面模型的建立可靠有效。

3.5 优化结果分析

基于已经建立的响应面模型，选择多目标遗传算法(MOCA)，以最大变形、二阶固有频率最大为优化目标，在材料的线性范围内，对实验设计点进行优化求解，最终得到表5所示的pareto最优解3个候选点。

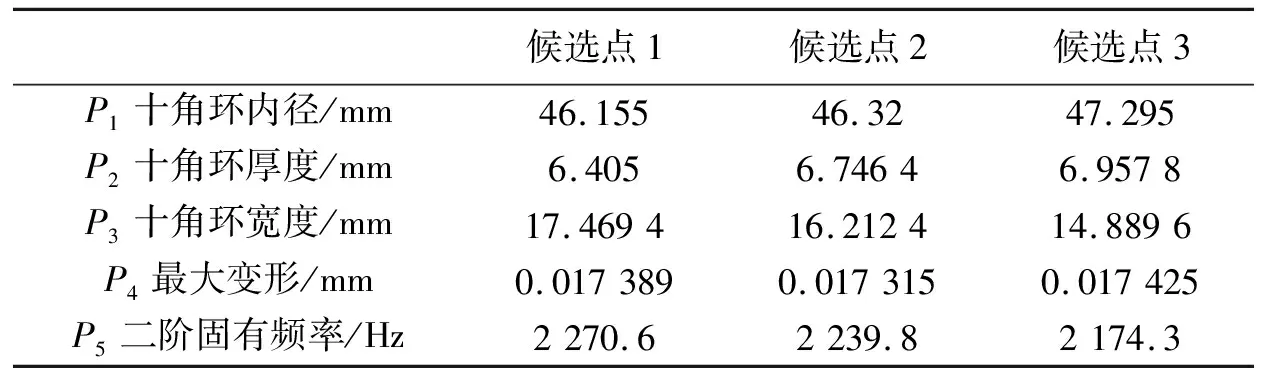
表5 优化候选点

经过对比分析，取候选点1各参数并圆整作为最优设计方案：十角环内径为46 mm、十角环厚度为6.5 mm、十角环宽度为17 mm，以此为最佳几何尺寸方案重新建立模型，再次对正交十角环结构进行静力分析和模态分析，获得优化后结构的最大变形为0.016 865 mm，二阶固有频率为2 183.4 Hz，与现有的正交八角环结构相比最大变形增大了6.6%，二阶固有频率增大了9.4%。

4 结论

测力仪弹性敏感结构设计过程中，结构的灵敏度和固有频率两者互相矛盾，获得较高的结构灵敏度就不可避免地牺牲结构的固有频率。针对这一关键问题，本文首次将响应面多目标优化方法用于测力仪弹性敏感结构优化设计，获得了十角环内径、厚度、宽度最优尺寸分别为46、6.5、8.5 mm；以该尺寸重新建立三维模型并进行有限元分析，结构的最大变形量、主切削力方向固有频率较八角环明显增大，有效改善了正交十角环结构的力学性能。综上所述，本文的研究可为十角环结构优化设计提供方法指导，该方法也可推广至其他测力仪弹性敏感结构的优化设计中。

后续工作中还需对优化后的正交十角环结构展开试验研究，与有限元结果进行对比验证，考虑到实际加工环境的复杂性，还需进一步对十角环结构封装的密闭性能进行试验。